图的建立基本操作

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h> // 添加头文件#define MAX_VERTEX_NUM 100 //图中最大顶点数//struct ArcNode* nextarc;
//ArcNode* firstarc;
//这两个是很有必要的,如果你没有这两个指针,你就无法判断当前的顶点是哪一个
// adj是邻接点,firstarc和nextarc分别代表当前和下一个点。//图的邻接表存储结构定义
typedef struct ArcNode {int adjvex; //邻接点在数组中的位置下标struct ArcNode* nextarc; //指向下一个邻接点的指针
} ArcNode;typedef struct VNode {char data; //顶点信息ArcNode* firstarc; //指向第一个邻接点的指针
} VNode, AdjList[MAX_VERTEX_NUM];//使用结构体嵌套的方式,把两个顶点还有边都给嵌套起来typedef struct {AdjList vertices; //邻接表,也就是顶点的意思int vexnum, arcnum; //顶点数和弧数bool is_directed; //是否是有向图
} ALGraph;//查找顶点的第一个邻接点
int FirstAdjVex(ALGraph G, int v)
{if (G.vertices[v].firstarc != NULL) {return G.vertices[v].firstarc->adjvex;}else {return -1; //返回“空”}
}//查找顶点的下一个邻接点int NextAdjVex(ALGraph G, int v, int w)
{ArcNode* p = G.vertices[v].firstarc;while (p != NULL && p->adjvex != w) {p = p->nextarc;}//先找到w先,题目说相对于w的下一个邻接点if (p != NULL && p->nextarc != NULL) {return p->nextarc->adjvex;}else {return -1; //返回“空”}
}//v是图中的某个顶点也就是 ArcNode* p,即G.vertices[v].firstarc;
//而p->adjvex != w这是v当前的邻接点
//那下一个邻接点自然就是 p->nextarc->adjvex了//一般节点的下一个节点就只有一个,
// 不是DFS不会一直往下面找,下一个就到空了,所以说是合理的循环。
//题目的意思就是说,w是v的临接节点。//插入一个新顶点
void InsertVex(ALGraph* G, char v)
{if (G->vexnum >= MAX_VERTEX_NUM) {printf("Error: The graph is full!\n");return;}G->vertices[G->vexnum].data = v;//存放点G->vertices[G->vexnum].firstarc = NULL;//存放其邻接点G->vexnum++;
}//删除一个顶点及其相关的弧
void DeleteVex(ALGraph* G, char v)
{int i, j;ArcNode* p, * q;i = LocateVex(*G, v);//找到顶点位置if (i == -1) {printf("Error: Vertex not found!\n");return;}//删除与该顶点相关的弧for (j = 0; j < G->vexnum; j++) {p = G->vertices[j].firstarc;//寻找每个图中的所有的第一个邻接点。while (p != NULL) {if (p->adjvex == i) {//如果邻接点是该下标的点q = p->nextarc;//因为是第一个邻接点,不存在有无前后的问题,所以直接接上下面一段就行了free(p);G->arcnum--;p = q;}else {//指针要动的只是邻接点为i的点//在它后面的点,直接下标往前移一位就行了if (p->adjvex > i) {p->adjvex--;//就是已经明确,我们要删除i点,// 那么其他所有的邻接点下标位置都要往前移1位//因为要删除i点了,那么所有的点的位置都要发生变化,就像数组那样//删除一个元素,全部元素都要往前移动。//至于前面的 if (p->adjvex == i) //那是因为直接将p点直接删除了,自然就不需要再管它的位置在哪里了}p = p->nextarc;//继续往下找,重复当前操作。}// 在这段代码中,adjvex属性表示一个弧所指向的顶点在图中的索引位置。// 当删除与指定顶点相关的弧时,如果不进行调整,// 那些位于指定顶点之后的顶点索引将会发生变化。//通过将p指向的弧的adjvex属性减1,可以确保顶点之间的编号连续性。// 也就是说,删除一个顶点之后,// 它之后的顶点的索引都需要减少1,以保持对应关系的正确性。// // 例如,假设原来顶点i之后的顶点分别为i + 1、i + 2、i + 3,// 删除与顶点i相关的弧之后,i + 1变成了i,i + 2变成了i + 1,i + 3变成了i + 2,以此类推。// 这样做的目的是为了在删除操作之后,// 依然可以通过顶点的索引来正确访问和操作图的邻接信息。}}//删除该顶点本身//弧跟顶点是不一样的概念for (j = i + 1; j < G->vexnum; j++) {G->vertices[j - 1] = G->vertices[j];}for (j = 0; j < G->vexnum; j++) {p = G->vertices[j].firstarc;while (p != NULL) {if (p->adjvex > i) {p->adjvex--;}p = p->nextarc;}}G->vexnum--;// 第一次循环是在删除与指定顶点相关的弧时进行的。//当找到邻接点的索引大于被删除顶点的索引时,将其减1,以保持顶点之间的编号连续性。// 第二次循环是在删除顶点本身后进行的。对于每个顶点,// 遍历其邻接链表,如果邻接点的索引大于被删除顶点的索引,// 则将其减1,同样是为了保持邻接信息的正确性。// 这两次循环的目的都是使得删除一个顶点后,// 其他顶点的索引发生相应变化,以确保后续的访问和操作仍然有效。}//邻接表表示当前顶点中
//分支到的任何一个下一个的顶点。
//
//而每一次都指针指向下一个然后删除原先的p节点。
//也就等于断开了所有与当前节点的链接,
//也就成功消除了它的所有弧了。//插入一条新弧
void InsertArc(ALGraph* G, char v, char w)
{int i, j;ArcNode* p, * q;i = LocateVex(*G, v);j = LocateVex(*G, w);if (i == -1 || j == -1) {printf("Error: Vertex not found!\n");return;}p = (ArcNode*)malloc(sizeof(ArcNode));p->adjvex = j;//邻接点是jp->nextarc = G->vertices[i].firstarc;//因为是插入,所以用next而非firstG->vertices[i].firstarc = p;//p代替了 G->vertices[i].firstarc//就是因为p中还有adj这个j的值,/*就是为了插入新弧才代替 G->vertices[i].firstarc的*///所以说原地址的 G->vertices[i].firstarc把它换成p就成功插入了。//p是新的头结点,所以原来的地址改成p的指针没毛病/* 首先,p->nextarc = G->vertices[i].firstarc; 将p的下一个指针指向顶点i的原第一个邻接边,这样p就成为了新的第一个邻接边。然后,G->vertices[i].firstarc = p;将顶点i的第一个邻接边指针指向p,即p成为了顶点i邻接表的新的第一个节点。*//* 又忘了指针偏移了,你记住,变动链表以后一定要把指针的头指向新的头结点,不然全部都错了!*/G->arcnum++;if (!G->is_directed) {q = (ArcNode*)malloc(sizeof(ArcNode));q->adjvex = i;q->nextarc = G->vertices[j].firstarc;G->vertices[j].firstarc = q;G->arcnum++;}
}
//p->adjvex 放置末端的点
//G->vertices[i].firstarc; 放置前端的点//问:p->nextarc = G->vertices[i].firstarc; 为什么不直接写成p = G->vertices[i].firstarc;?//这是因为G->vertices[i].firstarc是一个指向边表结构体的指针,
//而p是一个指向边表结构体的指针变量。
//如果将两者直接赋值,会导致p与G->vertices[i].firstarc指向同一块内存区域,
//任何一方对该内存区域的修改都会影响另一方。这可能不是我们期望的结果。
//
//正确的做法是让p指向与G->vertices[i].firstarc相同的内存地址,
//但是它们是两个不同的指针变量,互相独立,对其中一个指针变量的修改不会影响另一个。
//所以应该写成p->nextarc = G->vertices[i].firstarc,
//这样可以保证p指向与G->vertices[i].firstarc相同的内存地址,
//但是它们是两个不同的指针变量,互相独立,对其中一个指针变量的修改不会影响另一个。//总结:指针的特殊性问题,直接赋值就表示指向同一个地点,p指针就等于所指向的目标的地址。
//不独立,修改p也就等于修改了原地址的值。所以必须要用next才能成为独立的指针。
//相当于我只是使用了原地址的值,但我是作为独立的一个变量//删除一条弧
void DeleteArc(ALGraph* G, char v, char w)
{int i, j;ArcNode* p, * q;i = LocateVex(*G, v);j = LocateVex(*G, w);if (i == -1 || j == -1) {printf("Error: Vertex not found!\n");return;}p = G->vertices[i].firstarc;//从起点开始找q = NULL;while (p != NULL && p->adjvex != j) {q = p;//为什么要保存前面的顶点?//为了储存前面表的数据,方便后面衔接。p = p->nextarc;}if (p != NULL) {if (q == NULL) {G->vertices[i].firstarc = p->nextarc; //只有一个点的情况}else {q->nextarc = p->nextarc;}free(p);G->arcnum--;}if (!G->is_directed) {p = G->vertices[j].firstarc;q = NULL;while (p != NULL && p->adjvex != i) {q = p;p = p->nextarc;}if (p != NULL) {if (q == NULL) {G->vertices[j].firstarc = p->nextarc;}else {q->nextarc = p->nextarc;}free(p);G->arcnum--;}}
}//定位某个顶点的位置
int LocateVex(ALGraph G, char v)
{int i;for (i = 0; i < G.vexnum; i++) {if (G.vertices[i].data == v) {return i;}}return -1; //未找到
}int main()
{ALGraph G;G.is_directed = false; // 设置图为无向图G.vexnum = 0;G.arcnum = 0;InsertVex(&G, 'A');InsertVex(&G, 'B');InsertVex(&G, 'C');InsertVex(&G, 'D');InsertArc(&G, 'A', 'B');InsertArc(&G, 'A', 'C');InsertArc(&G, 'B', 'D');InsertArc(&G, 'C', 'D');printf("The first adjacent vertex of A is %c\n", G.vertices[0].firstarc->adjvex + 'A');printf("The next adjacent vertex of A after B is %c\n", NextAdjVex(G, 0, LocateVex(G, 'B')) + 'A');DeleteArc(&G, 'B', 'D');DeleteVex(&G, 'C');return 0;
}
相关文章:

图的建立基本操作
#include <stdio.h> #include <stdlib.h> #include <stdbool.h> // 添加头文件#define MAX_VERTEX_NUM 100 //图中最大顶点数//struct ArcNode* nextarc; //ArcNode* firstarc; //这两个是很有必要的,如果你没有这两个指针,你就无法判…...

影响语音芯片识别率的因素概述
语音芯片识别率是指芯片对人类语音信号的识别能力。在实际应用中,语音芯片识别率的高低直接影响了用户对芯片的体验和满意度。因此,提高语音芯片识别率是当前语音技术领域的重要任务之一。 1.、语音芯片的硬件设计:设计良好的芯片可以更好地…...

操作系统的主要功能--处理机、存储器、设备、文件
一、处理机管理功能 对处理机的管理可以归结为对进程的管理。处理机管理的主要功能包括:创建和撤销进程,对进程的运行进行协调,实现进程之间的信息交换,并且按照异地你给的算法将处理机分配给进程 进程控制:为一个作…...
PDF 批量处理软件BatchOutput PDF mac中文版介绍
BatchOutput PDF mac是一款适用于 Mac 的 PDF 批量处理软件。它可以帮助用户将多个 PDF 文件进行异步处理,提高工作效率。 BatchOutput PDF 可以自动化执行许多任务,包括 PDF 文件的打印、转换、分割、压缩、加密、重命名等,而且它还可以将自…...

oracle安装的肘腋之疾小合集
#临时空间指定 export TMP/tmp export TMPDIR/tmp #图形化显示框不全 java问题,使用系统自带的jre ./runInstaller -jreLoc/usr/local/jdk1.7.0_80/ #ins30131 Failed to access the temporary location 给/tmp/CVU*加x权限 #linux桌面太小 xrandr -s 1440x900_60…...
django(千锋教育)
创建一个django项目 官网下载python最新版本 配置到环境变量中 打开intlij编辑器 创建django项目 安装django:pip install django 创建django项目: django-admin startproject django01 创建djangoAPP:python manage.py startapp user 启动࿱…...
Python 前后端分离项目Vue部署应用
一、视图创建 from django.http import JsonResponse from django.shortcuts import render# Create your views here. from django.views import Viewclass IndexView(View):def get(self,request):# 前后端分离 (前端JS代码渲染数据)return JsonRespo…...

Linux中安装MySQ-合集
Linux中安装MySQL Centos中 1、卸载不必要的软件 先卸载mariadb安装MySQL必要环境 rpm -qa|grep mariadb rpm -e --nodeps mariadb-libs yum install -y gcc-c yum install net-tools yum -y install gcc如果需要Java等程序 yum install -y java* java-1.8.0-openjdk* op…...
elk 简单操作手册
1.1. 基础概念 EFK不是一个软件,而是一套解决方案,开源软件之间的互相配合使用,高效的满足了很多场合的应用,是目前主流的一种日志系统。 EFK是三个开源软件的缩写,分别表示:Elasticsearch , Filebeat, Kibana , 其中Elasticsearch负责日志保存和搜索,Filebeat负责收集日志,Ki…...
CSS画一条线
<p style"border: 1px solid rgba(0, 0, 0, 0.1);"></p> 效果:...
和几种关于设计模式的面试题)
分享常用设计模式之单例模式(懒汉模式和饿汉模式)和几种关于设计模式的面试题
目录 1.单例模式 1.懒汉模式 2.饿汉模式 2.设计一个不能被继承的类 3.设计一个不能被继承但是可以在外部环境创建该类对象的类 4.设计一个可以被继承但不能在外部环境创建该类的对象的类 5.限制派生类对象不能拷贝也不能赋值 1.单例模式 设计一个不能在外部环境创建该类…...

python每日一题——6三数之和
题目 给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i ! j、i ! k 且 j ! k ,同时还满足 nums[i] nums[j] nums[k] 0 。请 你返回所有和为 0 且不重复的三元组。 注意:答案中不可以包含重复的三元组。 …...
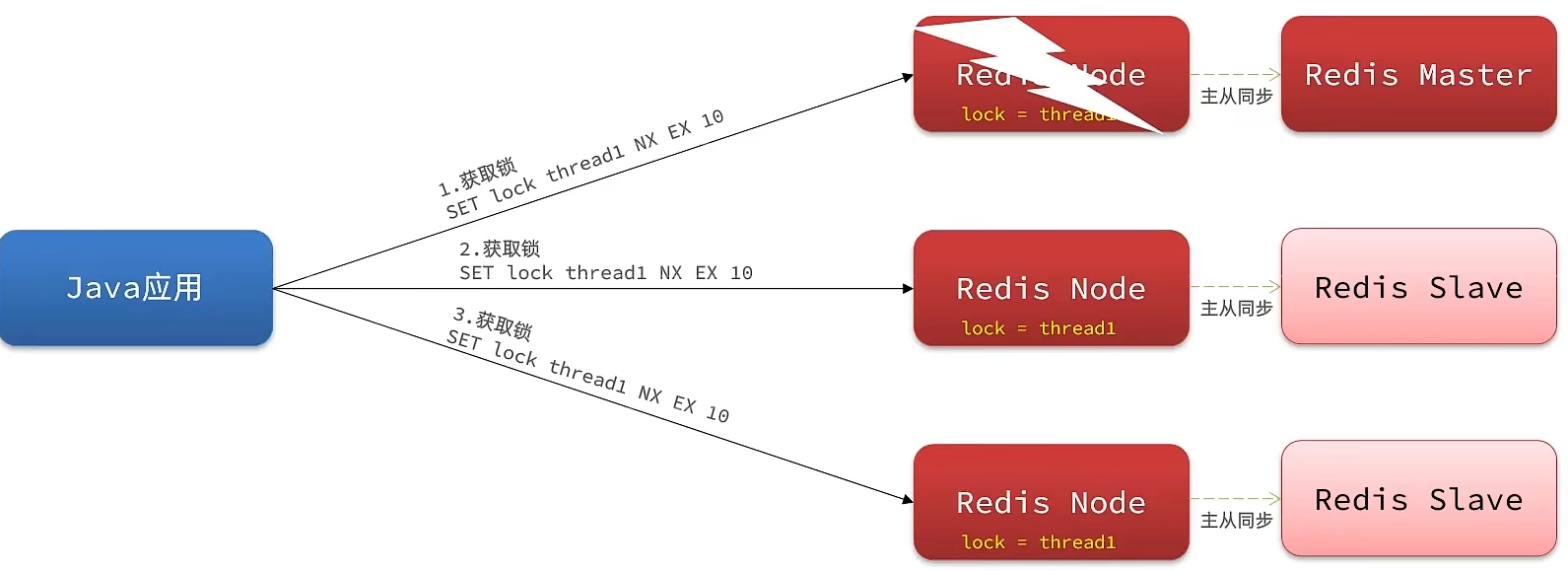
黑马点评笔记 分布式锁
文章目录 分布式锁基本原理和实现方式对比Redis分布式锁的实现核心思路实现分布式锁版本一Redis分布式锁误删情况说明解决Redis分布式锁误删问题分布式锁的原子性问题分布式锁-Redission分布式锁-redission可重入锁原理分布式锁-redission锁重试和WatchDog机制分布式锁-redissi…...

java---抽象类 用abstract修饰
抽象类是不能被[ 直接 ] [ 显式 ]实例化的如果抽象类中有一个抽象方法,那么这个类一定要声明为抽象类(反过来说,如果一个类是抽象类,那么它里面可以没有抽象方法)如果父类中有一个抽象方法,那么抽象的子类,要么也得是抽象的,要么就把抽象的方法全部给具体化(实现了) 抽象方法 …...

JVM 之 javac、java、javap 命令详解
目录 一. 前言 二. javac 命令 三. java 命令 四. javap 命令 一. 前言 在日常工作中,我们新建 Java工程,写好代码后,编译和运行几乎都是通过 IDE(如idea、eclipse)工具完成。但作为 Java开发者还是要了解下 Java虚…...

市场被套牢,没有了解积累和分配,昂首资本一一介绍
很多投资者对市场中的积累和分配的概念不是很清楚,下面昂首资本将一一介绍。 积累意味着尽可能多地买入筹码,而不大幅抬高价格,直到在你买入时的价格水平上没有或几乎没有筹码。这种买入通常发生在市场熊市之后,此时有最佳买入价…...

notion 3.0.0 版本最新桌面端汉化教程,支持MAC和WIN版本
notion客户端汉化(目前版本3.0.0) 最近notion桌面端更新了3.0.0版本后会导致老版本汉化失效,本项目实现了最新版Notion桌面端的汉化。 文件下载地址:汉化文件下载地址 项目说明 本项目针对新的客户端做了汉化文化,依…...

mysql union 和 union all区别?
在MySQL中,UNION和UNION ALL都是用于合并两个或多个SELECT语句的结果集。它们之间的主要区别在于如何处理重复记录。 UNION:UNION在合并结果集时会删除重复的记录。这意味着如果两个SELECT语句的输出结果中有相同的记录,那么UNION只会保留其中一个。在执…...

uni-app小程序 swiper 分页器样式修改
小程序中使用 wx-swiper-dot和wx-swiper-dot-active选择器 H5中使用uni-swiper-dot和uni-swiper-dot-active选择器 .swiper {height: 408px;margin-bottom: 28rpx;::v-deep .uni-swiper-dot {background: #e7e7e7;&.uni-swiper-dot-active {background: #b1b1b1;}}// #ifde…...

2023.11.23使用flask实现在指定路径生成文件夹操作
2023.11.23使用flask实现在指定路径生成文件夹操作 程序比较简单,实现功能: 1、前端输入文件夹 2、后端在指定路径生成文件夹 3、前端反馈文件夹生成状态 main.py from flask import Flask, request, render_template import osapp Flask(__name__)a…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

Linux安全加固:从攻防视角构建系统免疫
Linux安全加固:从攻防视角构建系统免疫 构建坚不可摧的数字堡垒 引言:攻防对抗的新纪元 在日益复杂的网络威胁环境中,Linux系统安全已从被动防御转向主动免疫。2023年全球网络安全报告显示,高级持续性威胁(APT)攻击同比增长65%,平均入侵停留时间缩短至48小时。本章将从…...
