Spring Boot中设置文件上传大小限制
在Spring Boot中,可以通过以下步骤来设置上传文件的大小:
在application.properties或application.yml文件中,添加以下配置:
对于application.properties:
spring.servlet.multipart.max-file-size=128MB
spring.servlet.multipart.max-request-size=128MB
对于application.yml:
spring: servlet: multipart: max-file-size: 128MB max-request-size: 128MB
这里的max-file-size是单个文件的最大大小,而max-request-size是整个请求的最大大小。可以根据需要调整这些值。
如果使用的是Spring Boot 1.x版本,还需要在启动类上添加MultipartConfigElement注解,如下所示:
java
import org.springframework.boot.web.servlet.MultipartConfigFactory;
import javax.servlet.MultipartConfigElement; @SpringBootApplication
public class YourApplication { public static void main(String[] args) { SpringApplication.run(YourApplication.class, args); } @Bean public MultipartConfigElement multipartConfigElement() { MultipartConfigFactory factory = new MultipartConfigFactory(); factory.setMaxFileSize("128MB"); factory.setMaxRequestSize("128MB"); return factory.createMultipartConfig(); }
}
但是,从Spring Boot 2.x开始,这一步就不再需要了,因为Spring Boot会自动配置这些属性。
通过以上配置,可以限制Spring Boot应用中的文件上传大小了。需要注意的是,这些限制不会在客户端进行,而是在服务端。因此,即使客户端尝试上传超过限制的文件,也只有在文件上传到服务器后才会发现这个问题。在实际应用中,可能还需要在客户端进行相应的检查和提示。
相关文章:

Spring Boot中设置文件上传大小限制
在Spring Boot中,可以通过以下步骤来设置上传文件的大小: 在application.properties或application.yml文件中,添加以下配置: 对于application.properties: spring.servlet.multipart.max-file-size128MB spring.se…...

8、独立按键控制LED显示二进制
独立按键控制LED显示二进制 #include <REGX52.H>void Delay(unsigned int xms) //12.000MHz {unsigned char i, j;while(xms--){i 2;j 239;do{while (--j);} while (--i);} }void main() {//数据类型刚好是8位与51单片机IO口寄存器位数相同(默认高电平&am…...
命名空间、字符串、布尔类型、nullptr、类型推导
面向过程语言:C ——> 重视求解过程 面向对象语言:C ——> 重视求解的方法 面向对象的三大特征:封装、继承和多态 C 和 C 在语法上的区别 1、命名空间(用于解决命名冲突问题) 2、函数重载和运算符重载…...

力控软件与多台PLC之间ModbusTCP/IP无线通信
Modbus TCP/IP 是对成熟的 Modbus 协议的改编, 因其开放性、简单性和广泛接受性而在工业自动化系统中发挥着举足轻重的作用。它作为连接各种工业设备的通用通信协议,包括可编程逻辑控制器 (PLC)、远程终端单元 (RTU) 和传感器。它提供标准化的 TCP 接口&…...

第96步 深度学习图像目标检测:FCOS建模
基于WIN10的64位系统演示 一、写在前面 本期开始,我们继续学习深度学习图像目标检测系列,FCOS(Fully Convolutional One-Stage Object Detection)模型。 二、FCOS简介 FCOS(Fully Convolutional One-Stage Object D…...

常用的git命令完整详细109条
Git是一个很强大的分布式版本控制系统,以下是一些常用的git命令: git init:在当前目录下创建一个新的Git仓库。git add 文件名:将指定的文件添加到暂存区,准备提交。git commit -m “备注”:提交暂存区的文…...

Ansible的错误处理
环境 管理节点:Ubuntu 22.04控制节点:CentOS 8Ansible:2.15.6 ignore_errors 使用 ignore_errors: true 来让Ansible忽略错误(运行结果是 failed ): --- - hosts: alltasks:- name: task1shell: cat /t…...
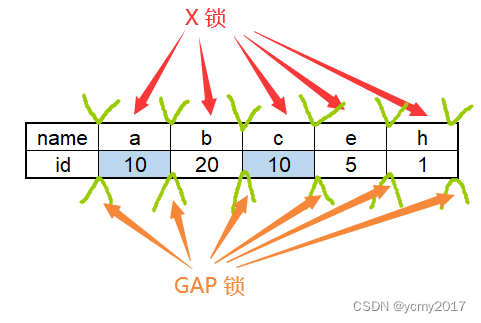
MySQL-04-InnoDB存储引擎锁和加锁分析
Latch一般称为闩锁(轻量级锁),因为其要求锁定的时间必须非常短。在InnoDB存储引擎中,latch又分为mutex(互斥量)和rwlock(读写锁)。 Lock的对象是事务,用来锁定的是…...

tcp/ip协议2实现的插图,数据结构2 (19 - 章)
(68) 68 十九1 选路请求与消息 函rtalloc,rtalloc1,rtfree (69) 69 十九2 选路请求与消息 函rtrequest (70)...
2023.11.22 -数据仓库的概念和发展
目录 https://blog.csdn.net/m0_49956154/article/details/134320307?spm1001.2014.3001.5501 1经典传统数仓架构 2离线大数据数仓架构 3数据仓库三层 数据运营层,源数据层(ODS)(Operational Data Store) 数据仓库层&#…...
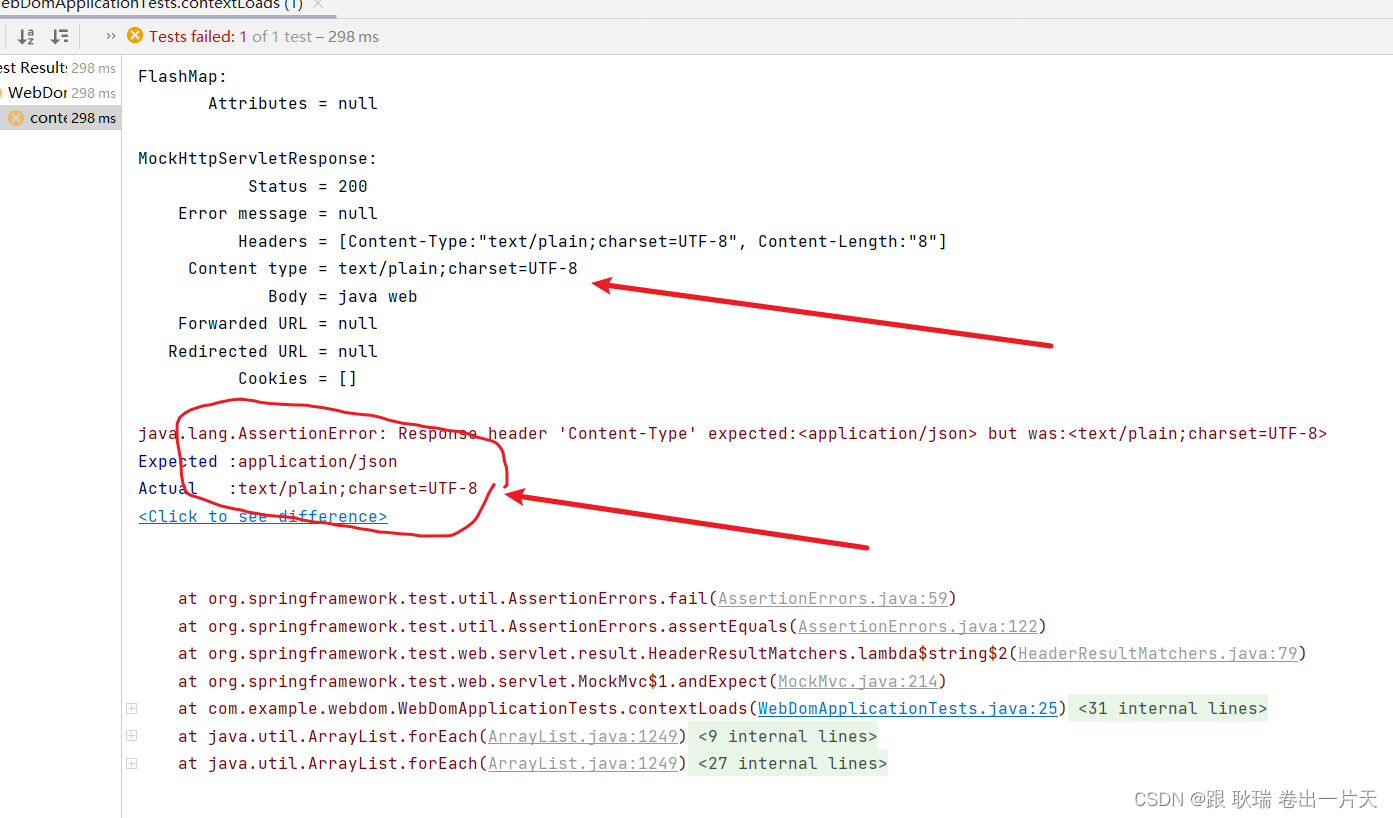
java springboot测试类虚拟MVC环境 匹配请求头指定key与预期值是否相同
上文 java springboot测试类虚拟MVC环境 匹配返回值与预期内容是否相同 (JSON数据格式) 版 中 我们展示 json匹配内容的方式 那么 本文我们来看看Content-Type属性的匹配方式 首先 我们从返回体可以看出 Content-Type 在请求头信息 Headers 中 我们直接将测试类代码更改如下 …...

Rust生态系统:探索常用的库和框架
大家好!我是lincyang。 今天我们来探索Rust的生态系统,特别是其中的一些常用库和框架。 Rust生态系统虽然相比于一些更成熟的语言还在成长阶段,但已经有很多强大的工具和库支持各种应用的开发。 常用的Rust库和框架 Serde:一个…...

01-了解微服务架构的演变过程和微服务技术栈
微服务 微服务架构演变 单体架构:将业务的所有功能集中在一个项目中开发最后打成一个包部署 优点: 架构简单, 部署成本低,适合小型项目缺点: 耦合度高, 升级维护困难 分布式架构:根据业务功能对系统做拆分,每个业务功能模块作为独立项目开发称为一个服务 优点: 降低服务耦合…...

阿里入局鸿蒙!鸿蒙原生应用再添两员新丁
今日HarmonyOS微博称,阿里钉钉、蚂蚁集团旗下的移动开发平台mPaaS与华为达成合作,宣布启动鸿蒙原生应用的开发!相关应用将以原生方式适配#HarmonyOS NEXT#系统。 #HarmonyOS#市场或迎来爆发式增长! 阿里钉钉 阿里钉钉与华为达成合…...
亚马逊运营中动态/静态住宅IP代理的应用有哪些?
作为全球最大的电商平台之一,亚马逊已经成为许多商家的首选销售平台。而代理IP作为近几天互联网的热门工具,在跨境电商界也起着非常强大的作用。那么在亚马逊运营中,适合动态住宅代理还是静态住宅代理呢?下面我们一起来探索&#…...
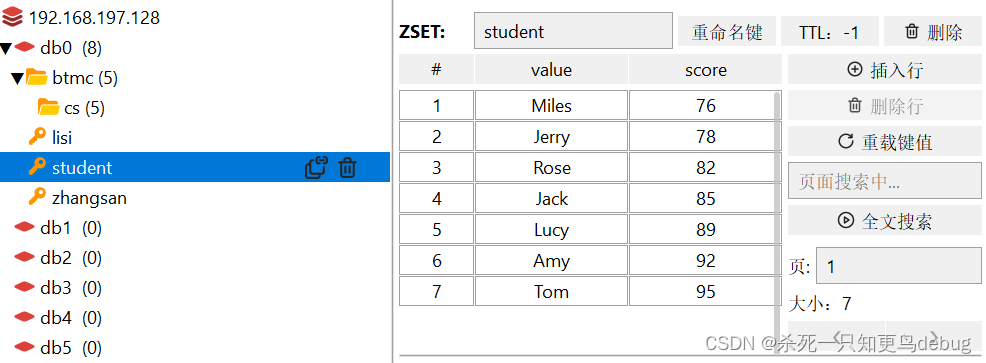
redis基本数据结构(String,Hash,Set,List,SortedSet)【学习笔记】
redis数据结构介绍 redis是一个key-value的数据库,key一般是String类型,但是value的类型多种多样。 redis 通用命令 keys : 查看符合模板的所有key (keys partten ,匹配表达式支持一些特殊字符 * ?)del:删…...
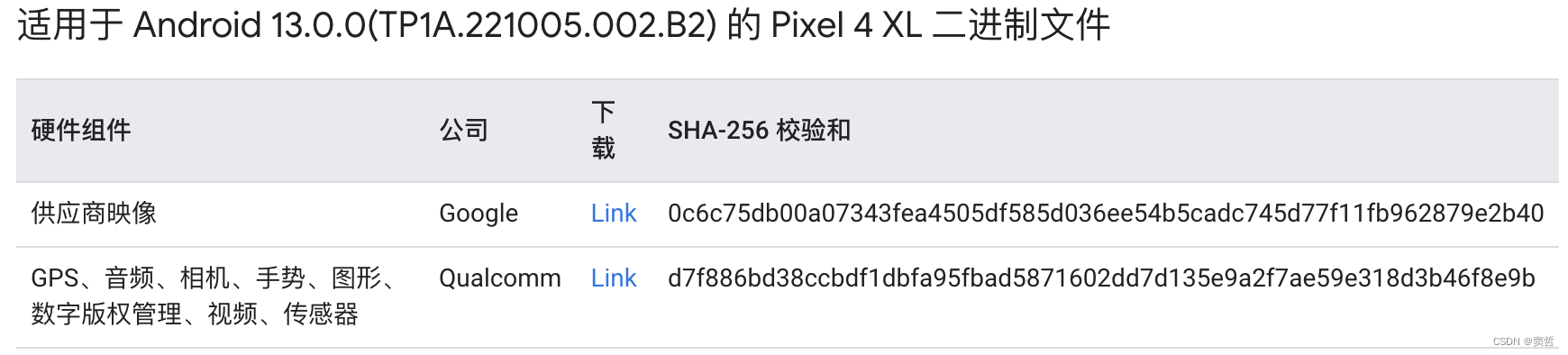
Ubuntu 22.04.3编译AOSP13刷机
文章目录 设备信息下载AOSP并切换分支获取设备驱动编译系统编译遇到的问题Cannot allocate memoryUbuntu设置USB调试刷机参考链接 设备信息 手机:Pixel 4XL 下载AOSP并切换分支 在清华大学开源软件镜像站下载初始化包aosp-latest.tar。 解压缩,切换到…...
Navicat 技术指引 | 适用于 GaussDB 的数据迁移工具
Navicat Premium(16.2.8 Windows版或以上) 已支持对 GaussDB 主备版的管理和开发功能。它不仅具备轻松、便捷的可视化数据查看和编辑功能,还提供强大的高阶功能(如模型、结构同步、协同合作、数据迁移等),这…...

算法基础之表达式求值
算法基础之表达式求值 中序表达式求值 用栈 将字符和数字分别用栈存储 由下往上计算 左子树算完再算右子树 判断方法:当前符号优先级<前一个符号优先级 则左右子树已遍历完 #include<iostream>#include<cstring>#include<stack>#include&l…...
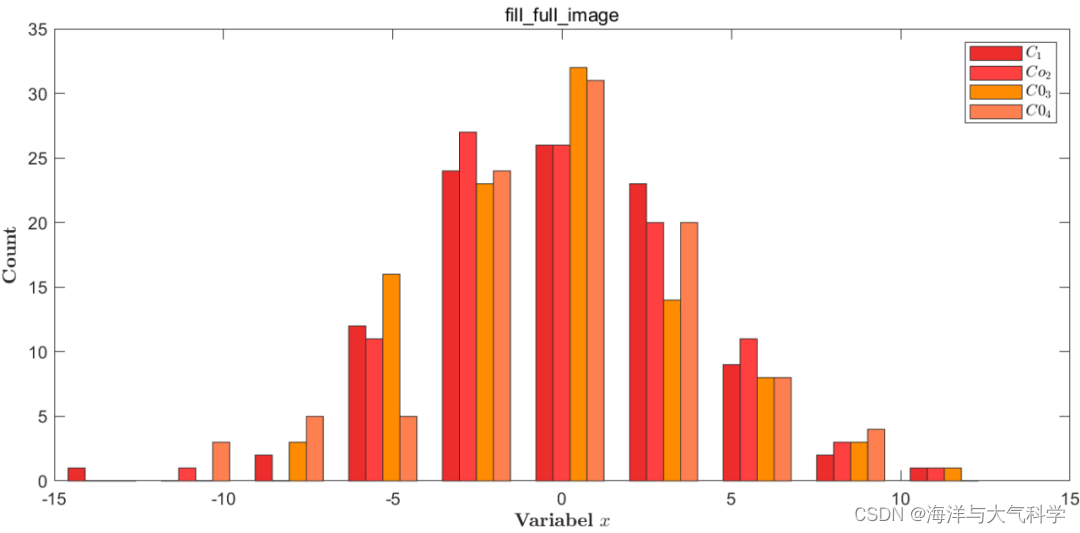
【matlab程序】图像最大化填充画布
【matlab程序】图像最大化填充画布 不做任何修饰: 修饰: 图片 往期推荐 图片 【python海洋专题一】查看数据nc文件的属性并输出属性到txt文件 【python海洋专题二】读取水深nc文件并水深地形图 【python海洋专题三】图像修饰之画布和坐标轴 【Pytho…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...
