递归方法来计算二叉树的双分支节点个数
1.递归方法来计算二叉树的双分支节点个数
首先,你需要定义二叉树的节点结构,然后编写递归函数
#include <stdio.h>
#include <stdlib.h>// 定义二叉树的节点结构
struct TreeNode {int value;struct TreeNode* left;struct TreeNode* right;
};// 创建新节点的函数
struct TreeNode* createNode(int value) {struct TreeNode* newNode = (struct TreeNode*)malloc(sizeof(struct TreeNode));newNode->value = value;newNode->left = NULL;newNode->right = NULL;return newNode;
}// 递归求解二叉树双分支节点个数的函数
int countDoubleBranchNodes(struct TreeNode* root) {if (root == NULL) {return 0;}// 判断当前节点是否为双分支节点int isDoubleBranch = (root->left != NULL && root->right != NULL);// 递归计算左右子树的双分支节点个数int leftCount = countDoubleBranchNodes(root->left);int rightCount = countDoubleBranchNodes(root->right);// 返回左右子树的双分支节点个数之和,加上当前节点的贡献return leftCount + rightCount + (isDoubleBranch ? 1 : 0);
}// 主函数
int main() {// 构建一个二叉树// 1// / \// 2 3// / \// 4 5struct TreeNode* root = createNode(1);root->left = createNode(2);root->right = createNode(3);root->left->left = createNode(4);root->left->right = createNode(5);// 计算双分支节点个数int result = countDoubleBranchNodes(root);printf("双分支节点个数: %d\n", result);// 释放动态分配的内存// 在实际应用中,确保释放分配的内存是很重要的// 此处为简化示例,没有包含详细的内存释放操作return 0;
}
2.C语言递归计算二叉树是否含有值为x的结点
#include <stdio.h>
#include <stdlib.h>// 定义二叉树节点结构
struct Node {int data;struct Node* left;struct Node* right;
};// 创建新节点
struct Node* newNode(int data) {struct Node* node = (struct Node*)malloc(sizeof(struct Node));node->data = data;node->left = NULL;node->right = NULL;return node;
}// 递归搜索二叉树中是否包含值为x的节点
int containsNode(struct Node* root, int x) {// 如果当前节点为空,返回0(未找到)if (root == NULL) {return 0;}// 如果当前节点的值等于x,返回1(找到了)if (root->data == x) {return 1;}// 递归搜索左子树和右子树int leftResult = containsNode(root->left, x);int rightResult = containsNode(root->right, x);// 返回左子树或右子树中是否找到了值为x的节点return leftResult || rightResult;
}int main() {// 创建二叉树struct Node* root = newNode(1);root->left = newNode(2);root->right = newNode(3);root->left->left = newNode(4);root->left->right = newNode(5);// 搜索值为x的节点int x = 3;if (containsNode(root, x)) {printf("二叉树中包含值为 %d 的节点。\n", x);} else {printf("二叉树中不包含值为 %d 的节点。\n", x);}return 0;
}
3.计算二叉树的高度
计算二叉树的高度和宽度可以通过递归的方式来实现。高度表示从根节点到最远叶子节点的最长路径长度,而宽度表示二叉树每一层的节点数的最大值。
#include <stdio.h>
#include <stdlib.h>// 定义二叉树节点结构
struct Node {int data;struct Node* left;struct Node* right;
};// 创建新节点
struct Node* newNode(int data) {struct Node* node = (struct Node*)malloc(sizeof(struct Node));node->data = data;node->left = NULL;node->right = NULL;return node;
}// 计算二叉树的高度(最大深度)
int getHeight(struct Node* root) {if (root == NULL) {return 0;} else {int leftHeight = getHeight(root->left);int rightHeight = getHeight(root->right);// 返回左右子树中的最大高度并加上根节点return (leftHeight > rightHeight) ? (leftHeight + 1) : (rightHeight + 1);}
}int main() {// 创建二叉树struct Node* root = newNode(1);root->left = newNode(2);root->right = newNode(3);root->left->left = newNode(4);root->left->right = newNode(5);root->right->left = newNode(6);root->right->right = newNode(7);// 计算二叉树的高度int height = getHeight(root);printf("二叉树的高度是: %d\n", height);return 0;
}
4.计算二叉树的宽度
要计算二叉树的宽度,可以通过层序遍历(广度优先搜索)的方式,记录每一层节点的数量,并找到最大的层的节点数。
这里提供一个计算二叉树宽度的函数:
#include <stdio.h>
#include <stdlib.h>// 定义二叉树节点结构
struct Node {int data;struct Node* left;struct Node* right;
};// 创建新节点
struct Node* newNode(int data) {struct Node* node = (struct Node*)malloc(sizeof(struct Node));node->data = data;node->left = NULL;node->right = NULL;return node;
}// 获取二叉树的高度
int getHeight(struct Node* root) {if (root == NULL) {return 0;} else {int leftHeight = getHeight(root->left);int rightHeight = getHeight(root->right);return (leftHeight > rightHeight) ? (leftHeight + 1) : (rightHeight + 1);}
}// 辅助函数:递归地计算每一层的节点数
void getWidthRecursive(struct Node* root, int level, int* count) {if (root == NULL) {return;}if (level == 1) {(*count)++;} else if (level > 1) {getWidthRecursive(root->left, level - 1, count);getWidthRecursive(root->right, level - 1, count);}
}// 计算二叉树的宽度
int getWidth(struct Node* root) {int maxWidth = 0;int height = getHeight(root);for (int i = 1; i <= height; i++) {int count = 0;getWidthRecursive(root, i, &count);if (count > maxWidth) {maxWidth = count;}}return maxWidth;
}int main() {// 创建二叉树struct Node* root = newNode(1);root->left = newNode(2);root->right = newNode(3);root->left->left = newNode(4);root->left->right = newNode(5);root->right->left = newNode(6);root->right->right = newNode(7);// 计算二叉树的宽度int width = getWidth(root);printf("二叉树的宽度是: %d\n", width);return 0;
}
这两个示例展示了如何使用递归方法计算二叉树的高度和宽度。函数 getHeight 用于计算二叉树的高度,而 getWidth 函数则使用辅助函数 getWidthRecursive 来计算每一层的节点数,从而得到二叉树的宽度。
相关文章:

递归方法来计算二叉树的双分支节点个数
1.递归方法来计算二叉树的双分支节点个数 首先,你需要定义二叉树的节点结构,然后编写递归函数 #include <stdio.h> #include <stdlib.h>// 定义二叉树的节点结构 struct TreeNode {int value;struct TreeNode* left;struct TreeNode* righ…...
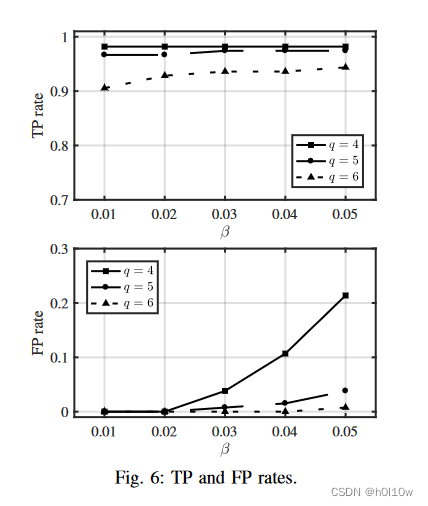
INFLOW:用于检测隐藏服务器的反向网络流水印
文章信息 论文题目:INFLOW: Inverse Network Flow Watermarking for Detecting Hidden Servers 期刊(会议):IEEE INFOCOM 2018 - IEEE Conference on Computer Communications 时间:2018 级别:CCF A 文章链…...

社区物联网云服务架构设计
文章目录 1 摘要2 架构图2.1 社区物联网云服务网络拓扑图2.2 社区物联网云服务通讯流程图2.3 社区远程开锁功能流程图 3 应用场景 1 摘要 随着社区管理越来越智能化,社区物联网升级与改造的市场空间也越来越大。社区物联网包含楼宇对讲、门禁门锁、通道闸等等设备系…...

Linux - 文件系统 - 理解目录 - 理解 软/硬链接
前言 在上篇博客当中,我们对 文件系统 和 inode 做了初步了解,本博客将在上篇博客的基础之上,对于 文件系统当中的目录进行进步一阐述。 Linux - 进一步理解 文件系统 - inode - 机械硬盘-CSDN博客 目录 一个文件有一个 inode,…...

Springboot websocket前端无法访问到,Websocket因AOP代理 前端无法请求到
Springboot websocket前端无法访问到,Websocket因AOP代理 前端无法请求到 问题出现 在我后端springboot启动后,前端无法请求websocket请求连接到我们websocket服务器。 想要的效果 在我后端springboot启动后,前端可以请求到我们websocket…...

基于高质量训练数据,GPT-4 Turbo更出色更强大
11月7日消息,OpenAI在首届开发者大会上正式推出了GPT-4 Turbo。 与GPT-4相比,GPT-4 Turbo主要有6方面的提升: 1、扩展下文对话长度:GPT4最大只能支持8k的上下文长度(约等于6000个单词),而GPT-4…...
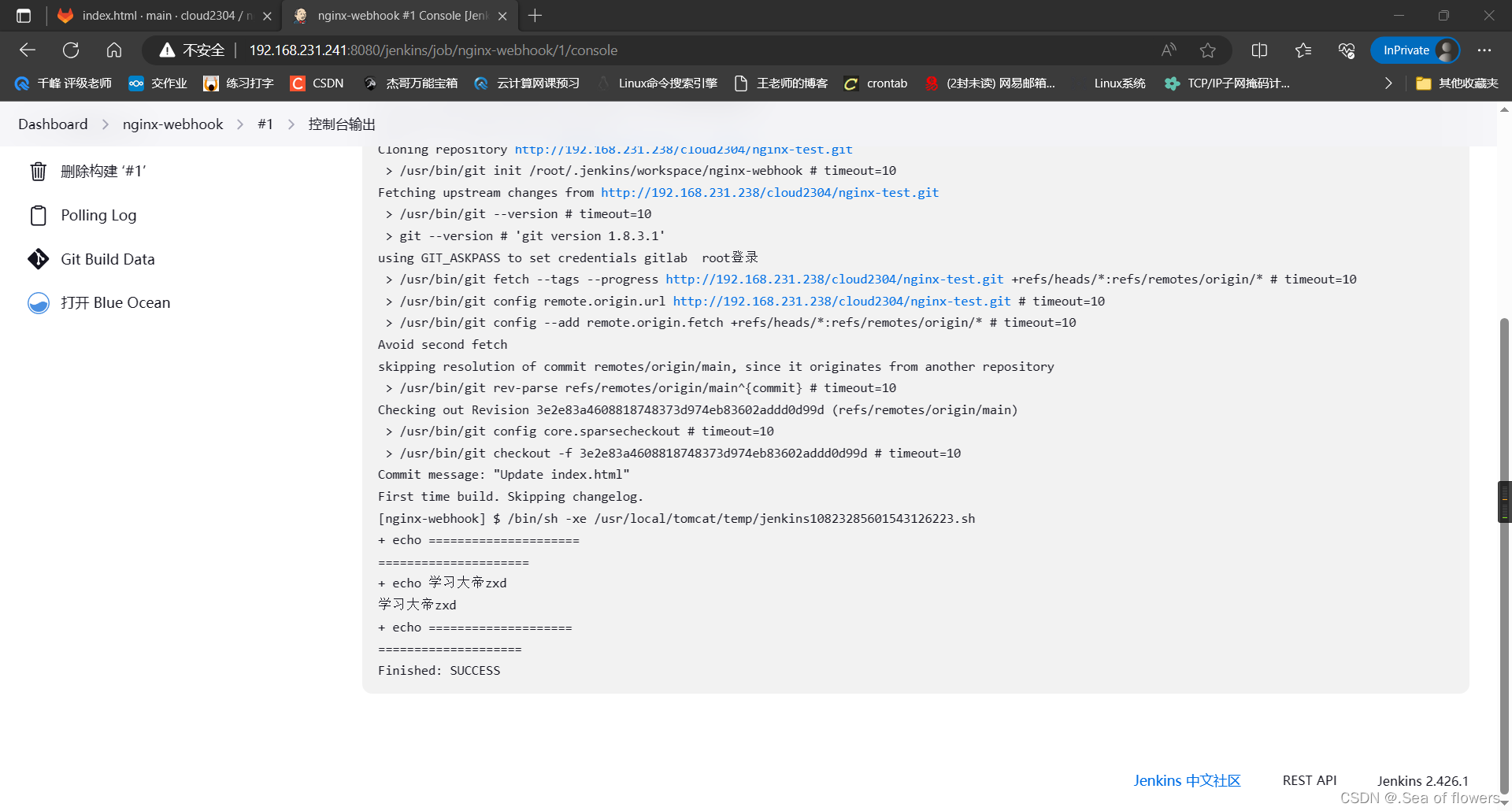
jenkins + gitlab 自动部署(webhook)
Jenkins是一个流行的开源CI/CD工具,可以与Git等版本控制系统集成,实现自动构建、测试和部署。Webhook是一种机制,可以在Git仓库中设置,在代码提交或合并请求时触发Jenkins构建任务,以完成自动化部署。 实操 设备信息 …...
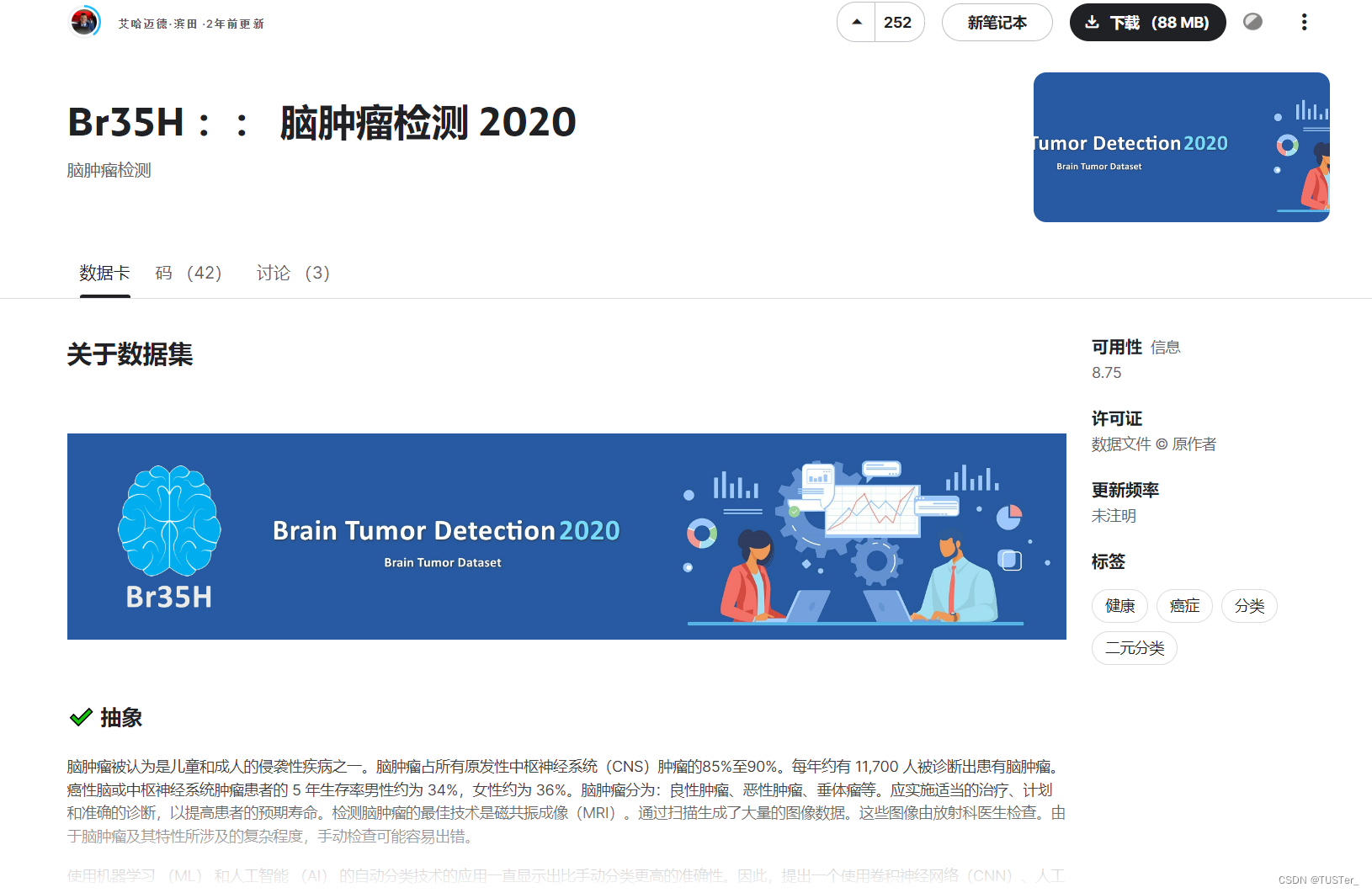
【数据集】全网最全的常见已公开医学影像数据集
目录 一,极市医学数据集汇总 1.CT 医学图像 编辑 2.恶性与良性皮肤癌 3.白内障数据集 4.胸部 X 光图像(肺炎) 5.用于图像增强的内窥镜真实合成曝光过度和曝光不足帧 6.医学家 7.乳房组织病理学图像 8.皮肤癌 MNIST:HA…...

图形数据库的实战应用:如何在 Neo4j 中有效管理复杂关系
关系数据库管理系统( RDBMS ) 代表了最先进的技术,这在一定程度上要归功于其由周边技术、工具和广泛的专业技能组成的完善的生态系统。 在这个涵盖信息技术(IT) 和运营技术(OT) 的技术革命时代,人们普遍认识到性能方面出现了重大挑战,特别是…...
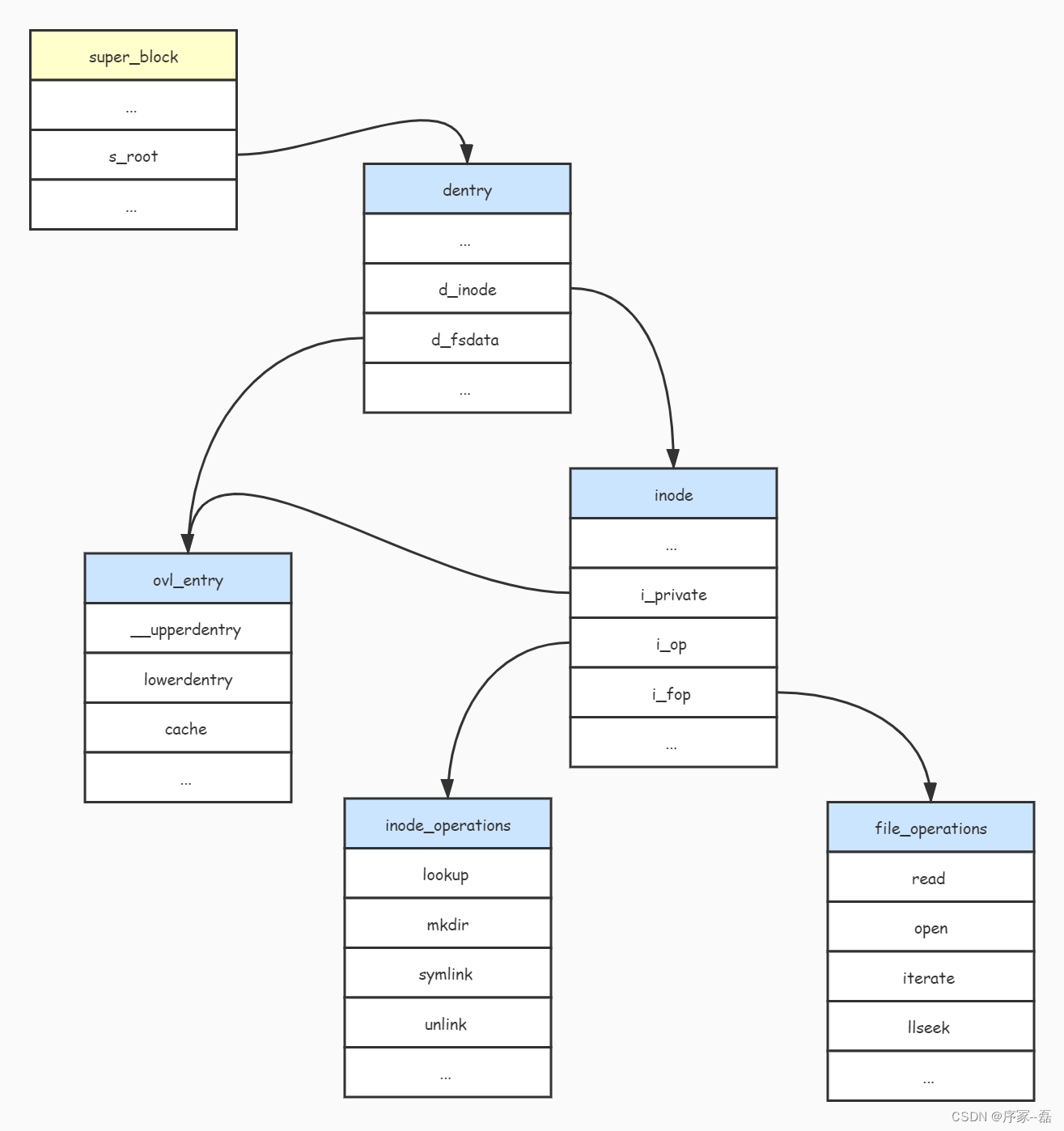
Linux内核中的overlay文件系统
一、简介 Docker 内核实现容器的功能用了linux 内核中的三个特性 Namespace、Cgroup、UnionFs,今天我们来说一下UnionFs。 linux UnionFs 实现的是overlay 文件系统 OverlayFs 文件系统分为三层, lower 是只读层 Upper 是可读写 Merged 是 lower 和U…...
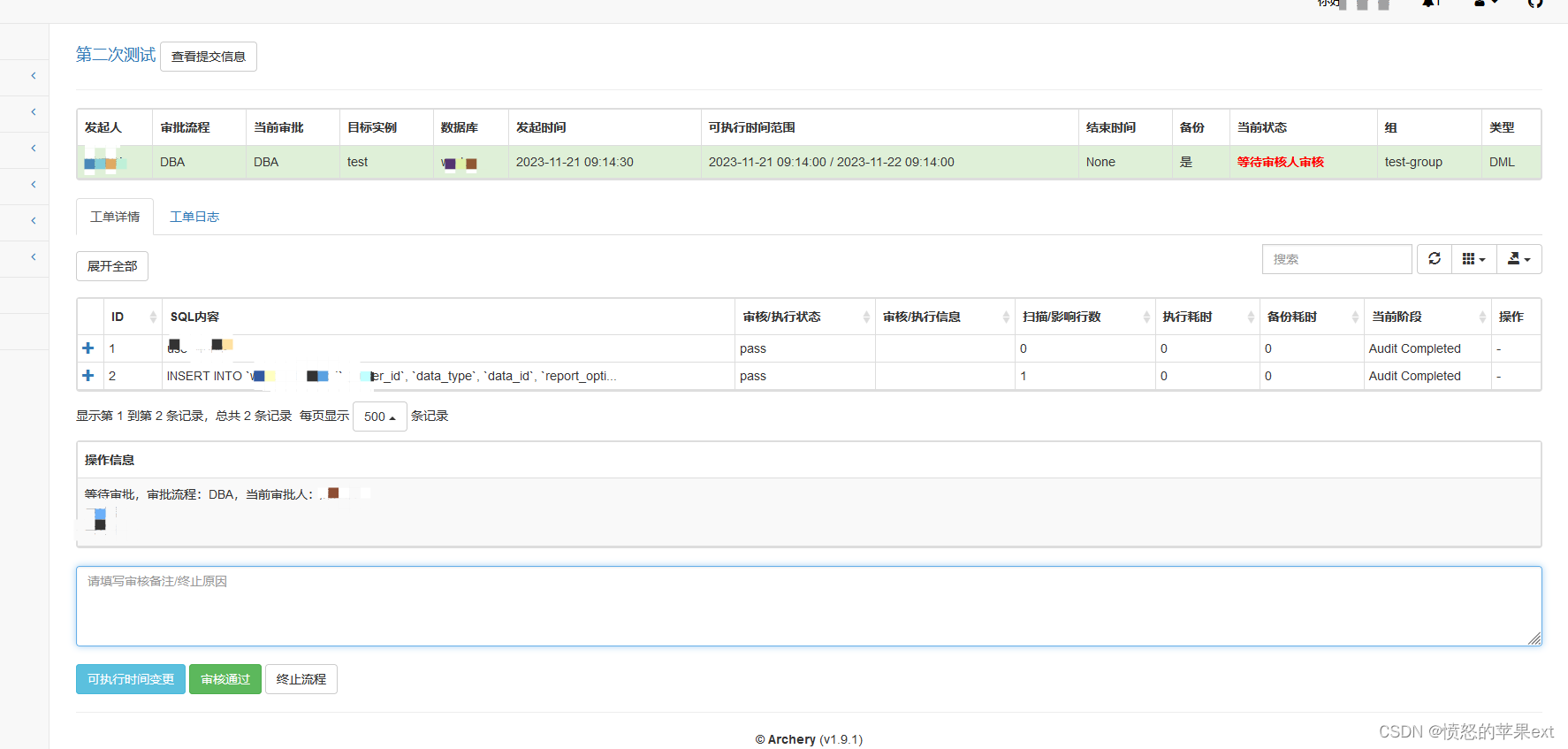
archery修改为不能自提自审核上线SQL
目录 背景修改代码效果参考 背景 我和同事都可以提交上线SQL,但是不能自己提交的SQL自己去审核通过。目前的情况是可以自提自审。 修改代码 找到/opt/archery/sql/utils/workflow_audit.py文件 ...省略...# 判断用户当前是否是可审核staticmethoddef can_revie…...
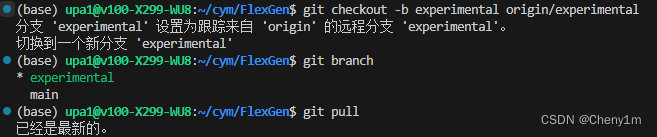
如何处理git多分支
本篇文章主要处理以下两种多分支问题 如何将自己在本地的修改上传到一个新的Git分支(比如用于测试,不合并进main分支)?如何在一个新的本地仓库拉取一个项目的非main分支,并处理他们关联关系? 1. 将自己在…...

Proteus仿真--基于DS1302与数码管设计的可调电子钟
本文主要介绍基于51单片机的DS1302的可调式电子钟实验(完整仿真源文件及代码见文末链接) 仿真图如下 其中数码管显示电子钟时间信息,按键用于调节时间,时间芯片选用DS1302芯片 仿真运行视频 Proteus仿真--基于DS1302与数码管设…...

ESP32网络开发实例-远程Web串口监视器
远程Web串口监视器 文章目录 远程Web串口监视器1、应用介绍2、软件准备3、硬件准备4、代码实现在本文中,我们将构建一个 ESP32 网络服务器,用作远程串行监视器。 基于 Web 的串行监视器的工作方式与通常用于调试目的的 Arduino IDE 串行监视器的工作方式相同。 1、应用介绍 …...
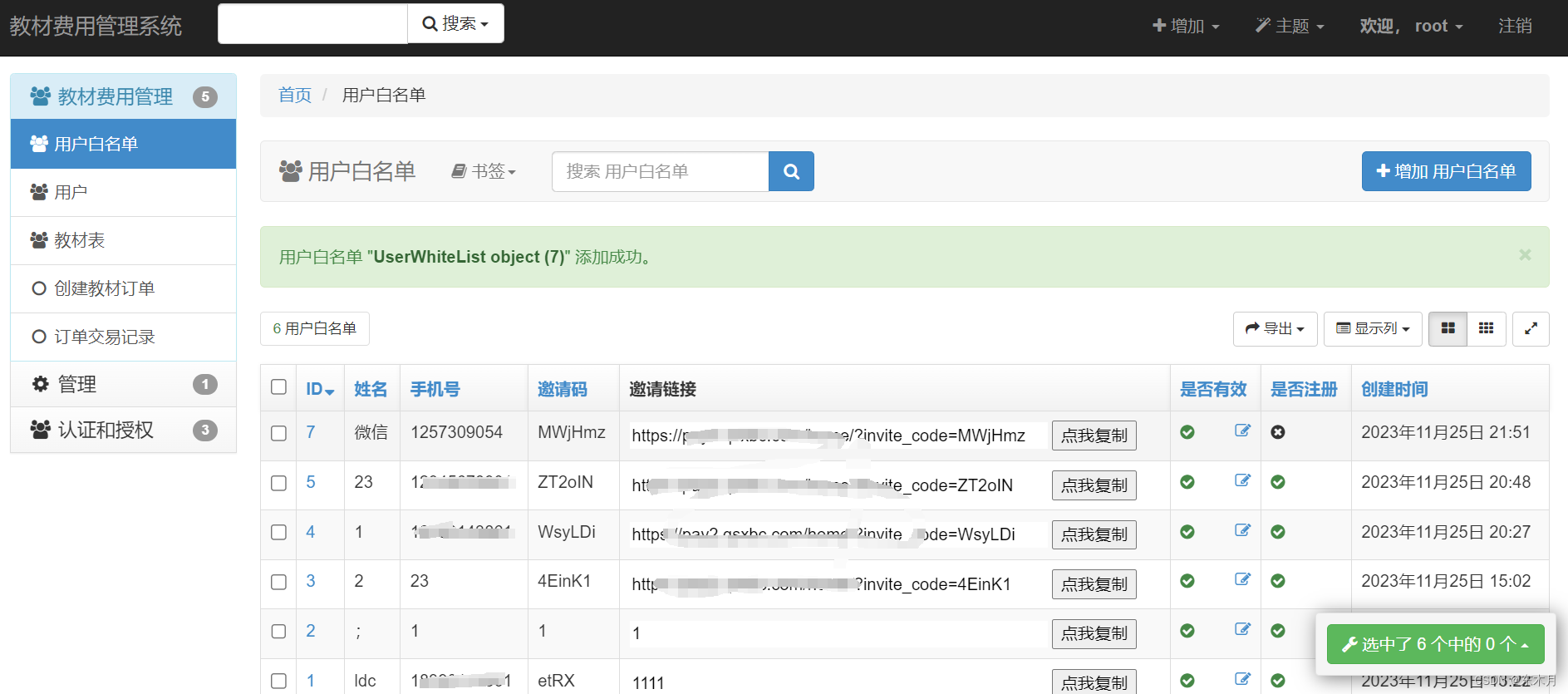
xadmin后台在每一行记录增加一个复制链接按钮
xadmin后台在每一行记录增加一个复制链接按钮 1、效果 点击复制后,自动把url链接复制到粘贴板,按Ctrl+v即可显示复制内容。 2、实现代码 adminx.py # 用户管理 class UserWhiteListAdmin(object):search_fields = [name, mobile] # 检索字段list_display...
LVS+Keepalived 高可用群集
一、一.Keepalived工具介绍 专为LVS和HA设计的一款健康检查工具 • 支持故障自动切换(Failover) • 支持节点健康状态检查(Health Checking) • 官方网站:http://www.keepalived.org/ 二、Keepalived工作原理 • …...

数据传输的思考
Wi-Fi:Wi-Fi是一种无线网络技术,可以用于无线互联网接入、局域网通信和数据传输等。Wi-Fi基于IEEE 802.11标准,通过无线信号传输数据,提供高速的无线网络连接。Wi-Fi可用于连接设备与路由器或者设备之间的直接通信,可以…...
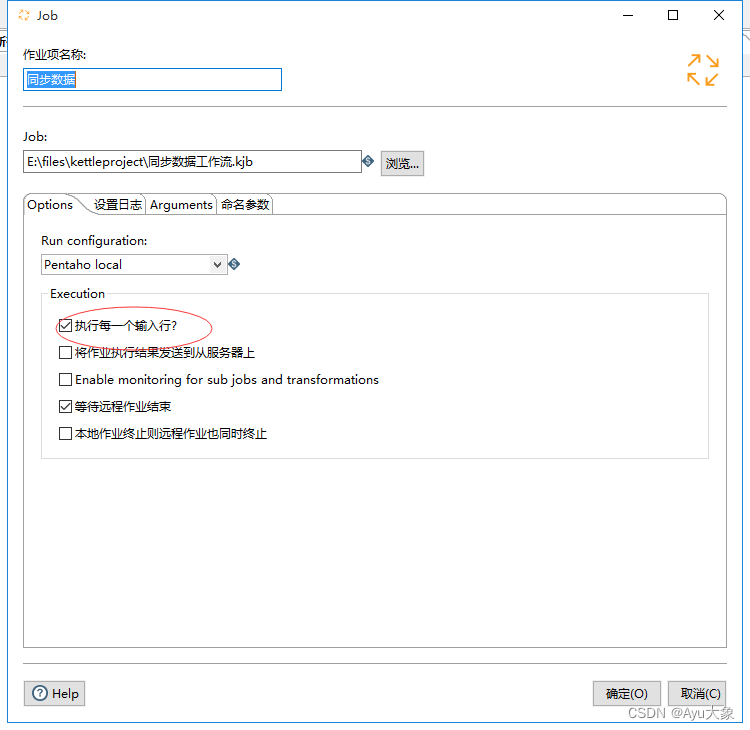
ETL-使用kettle批量复制sqlserver数据到mysql数据库
文章标题 1、安装sqlserver数据库2、下载kettle3、业务分析4、详细流程(1)转换1:获取sqlserver所有表格名字,将记录复制到结果(2)转换2:从结果设置变量(3)转换3ÿ…...
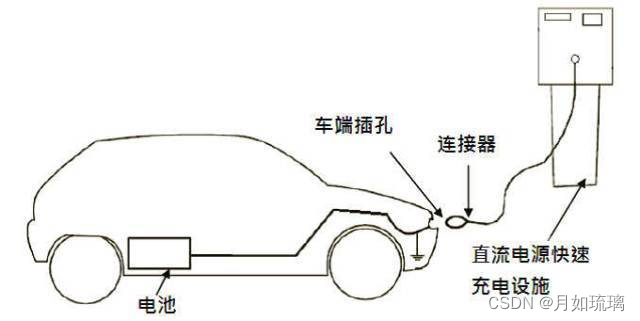
交流充电桩与直流充电桩的区别
1、背景 直流充电桩的学名是非车载充电机,是相对于交流充电桩而言的。交流充电桩是采用传导方式为具备车载充电机的电动汽车提供交流电能的专用装置。 2、交流充电桩和直流充电桩 1.1、交流充电桩 交流充电桩包括单相和三相交流充电桩。 图一是交流充电桩原理框…...

基于单片机公交安全预警系统仿真设计
**单片机设计介绍, 基于单片机公交安全预警系统仿真设计 文章目录 一 概要二、功能设计设计思路 三、 软件设计原理图 五、 程序六、 文章目录 一 概要 基于单片机的公交安全预警系统可以被设计成能够实时监测公交车辆的行驶状态,并在发生异常情况时进行…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...
