【数据结构实验】图(一)Warshall算法(求解有向图的可达矩阵)
文章目录
- 1. 引言
- 2. Warshall算法原理
- 2.0 图的基础知识
- a. 类型
- b. 表示
- 2.1 初始化可及矩阵
- 2.2 迭代更新可及矩阵
- 3. 实验内容
- 3.1 实验题目
- (一)输入要求
- (二)输出要求
- 3.2 算法实现
- 4. 实验结果
1. 引言
Warshall算法是一种用于求解有向图的可达矩阵的经典算法,算法通过迭代更新图的可达矩阵,从而找到图中任意两个顶点之间的可达关系。
本文将介绍Warshall算法的实现细节,并通过一个具体的例子进行演示。
2. Warshall算法原理
2.0 图的基础知识
a. 类型
图(Graph)是由节点(Vertex)和节点之间的边(Edge)组成的一种数据结构。图可以用来表示不同对象之间的关系或连接方式。在图中,每个节点代表一个对象,而边则表示节点之间的关系或连接。根据边的性质,图可以分为有向图(Directed Graph)和无向图(Undirected Graph)两种类型。
-
有向图是指图中的边具有方向性,表示节点之间的单向关系。例如,如果节点A指向节点B的边存在,则从节点A可以到达节点B,但从节点B无法直接到达节点A。有向图中的边可以是单向的,也可以是双向的。
-
无向图是指图中的边没有方向性,表示节点之间的双向关系。无向图中的边是双向的,即从节点A可以到达节点B,同时从节点B也可以到达节点A。
b. 表示
图可以用多种方式表示,常见的有邻接矩阵(Adjacency Matrix)和邻接表(Adjacency List)两种形式。
-
邻接矩阵是一个二维数组,用于表示节点之间的连接关系。对于有向图,邻接矩阵的元素表示从一个节点到另一个节点的边的存在与否;对于无向图,邻接矩阵是对称的。
-
邻接表是一种链表数组的形式,用于表示每个节点和与之相连的边。对于每个节点,邻接表中存储了与该节点直接相连的所有节点的信息。
2.1 初始化可及矩阵

遍历图的边集,根据边的关系初始化可及矩阵。如果有一条边连接顶点 Vi 和 Vj,则将可及矩阵的相应位置设为 1。
2.2 迭代更新可及矩阵

通过三重循环嵌套,对可及矩阵进行迭代更新。如果发现存在一个顶点 Vk,使得从顶点 Vi 经过 Vk 到达顶点 Vj,则将可及矩阵中 Vi 和 Vj 之间的位置设为 1。
3. 实验内容
第一题. 实现书上 204 页的 Warshall 算法,求图 G 的可及矩阵。
(一) 输入数据
上面的邻接矩阵。
(二)输出要求
3.1 实验题目
实现Warshall 算法, 求图的可及矩阵
(一)输入要求
{0,1,1,1,1,0,0},
{0,0,1,1,0,0,0},
{1,0,0,0,0,0,0},
{0,0,1,0,0,0,0},
{0,0,0,0,0,1,1},
{0,0,0,0,0,0,1},
{0,0,0,0,0,0,0}
(二)输出要求
- 输出可及矩阵。
- 输出任意两个不相邻顶点 i,j 的具体可及信息,即顶点 i,j 因为哪个顶点可及(以打印语句形式输出)。
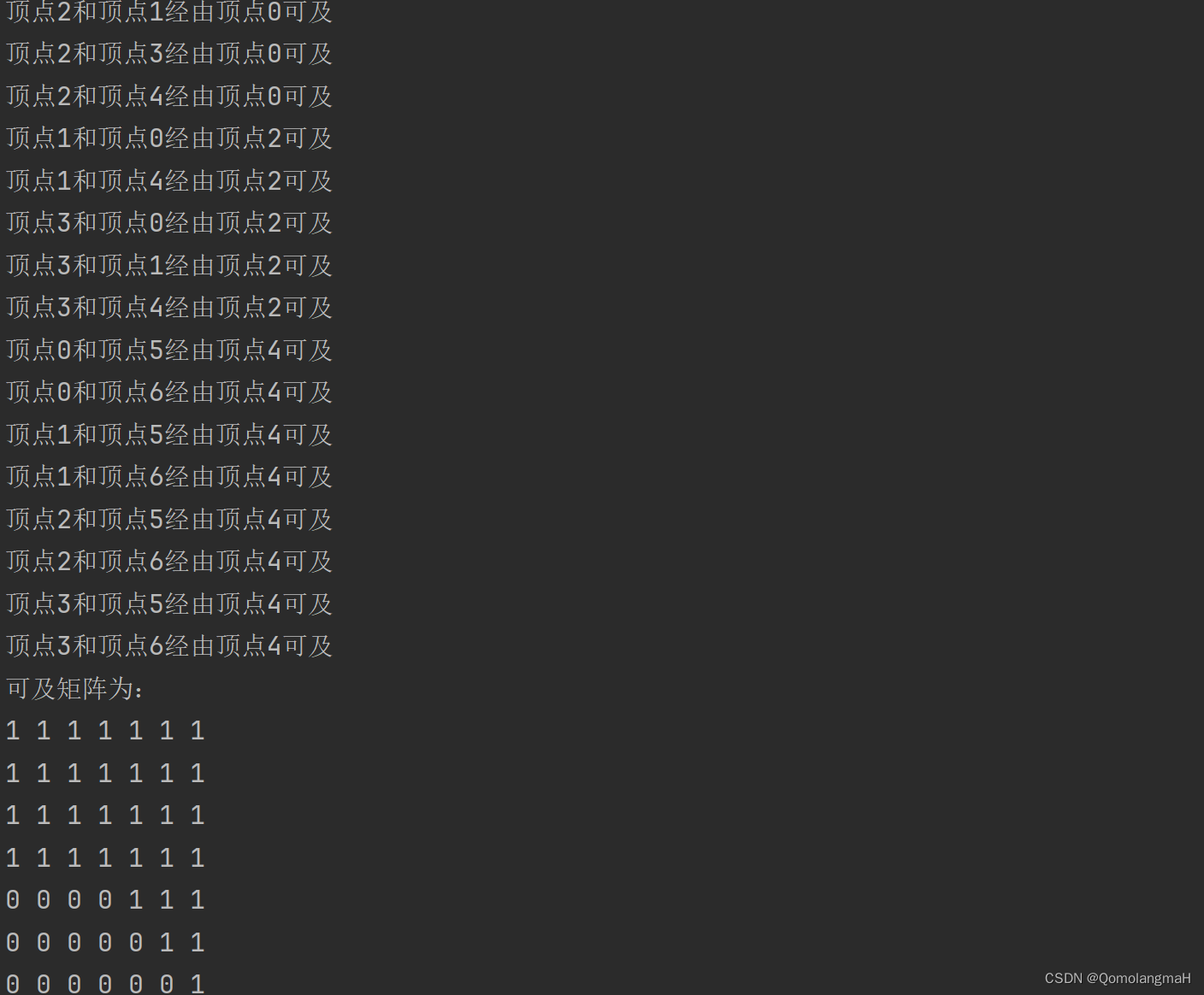
提示:当程序计算出某两个不相邻顶点 i,j 可及时,输出此语句,形如:“顶点 i 和顶点 j 经由顶点 v 可及。
3.2 算法实现
#include<stdio.h>
#define N 7void Warshall(int A[][N]) {int B[N][N] = {0}, i, j, k, t = 0;// 初始化可及矩阵for (i = 0; i < N; i++)for (j = 0; j < N; j++)B[i][j] = (i == j) ? 1 : (A[i][j] == 1) ? 1 : 0;// 迭代更新可及矩阵for (k = 0; k < N; k++) {for (i = 0; i < N; i++) {if (B[i][k]) {for (j = 0; j < N; j++) {t = 0;if (B[i][j] == 0) t = 1;B[i][j] = B[i][j] || B[k][j];if (B[i][j] && t) printf("顶点%d和顶点%d经由顶点%d可及\n", i, j, k);}}}}// 打印可及矩阵printf("可及矩阵为:\n");for (i = 0; i < N; i++) {for (j = 0; j < N; j++)printf("%d ", B[i][j]);printf("\n");}
}int main() {int A[N][N] = {{0, 1, 1, 1, 1, 0, 0},{0, 0, 1, 1, 0, 0, 0},{1, 0, 0, 0, 0, 0, 0},{0, 0, 1, 0, 0, 0, 0},{0, 0, 0, 0, 0, 1, 1},{0, 0, 0, 0, 0, 0, 1},{0, 0, 0, 0, 0, 0, 0}};Warshall(A);return 0;
}
这个程序会输出可及矩阵,并在更新矩阵的过程中打印出经由哪些顶点可以到达其他顶点。
4. 实验结果
相关文章:

【数据结构实验】图(一)Warshall算法(求解有向图的可达矩阵)
文章目录 1. 引言2. Warshall算法原理2.0 图的基础知识a. 类型b. 表示 2.1 初始化可及矩阵2.2 迭代更新可及矩阵 3. 实验内容3.1 实验题目(一)输入要求(二)输出要求 3.2 算法实现 4. 实验结果 1. 引言 Warshall算法是一种用于求解…...
java协同过滤算法 springboot+vue游戏推荐系统
随着人们生活质量的不断提高以及个人电脑和网络的普及,人们的业余生活质量要求也在不断提高,选择一款好玩,精美,画面和音质,品质优良的休闲游戏已经成为一种流行的休闲方式。可以说在人们的日常生活中,除了…...

Android设计模式--适配器模式
至诚之道,可以前知 一,定义 适配器模式把一个类的接口变换成客户端所期待的另一种接口,从而使原本因接口不匹配而无法在一起工作的两个类能够在一起工作。 适配器模式在我们的开发中使用率极高,ListView,GridView&am…...

jQuery_06 基本过滤器的使用
什么是过滤器? 过滤器就是用来筛选dom对象的,过滤器是和选择器一起使用的。在选择了dom对象后在进行过滤筛选。 jQuery对象中存储的dom对象顺序与页面标签声明有关系。 声明顺序就是dom中存放的顺序 1.基本过滤器 使用dom对象在数组中的位置来作为过滤条…...
Kotlin学习——kt里面的函数,高阶函数 函数式编程 扩展函数和属性
Kotlin 是一门现代但已成熟的编程语言,旨在让开发人员更幸福快乐。 它简洁、安全、可与 Java 及其他语言互操作,并提供了多种方式在多个平台间复用代码,以实现高效编程。 https://play.kotlinlang.org/byExample/01_introduction/02_Functio…...
AI绘画“湿地公园的美女”
1、AI绘画:湿地公园的美女 通过输入描述:你需要什么场景的什么创作内容,AI根据内容创造出适合的主题 如图所示:请帮我创作一个湿地公园的像高圆圆的美女图片。 输出的结果如下:总体来说感觉还是非常快,基…...
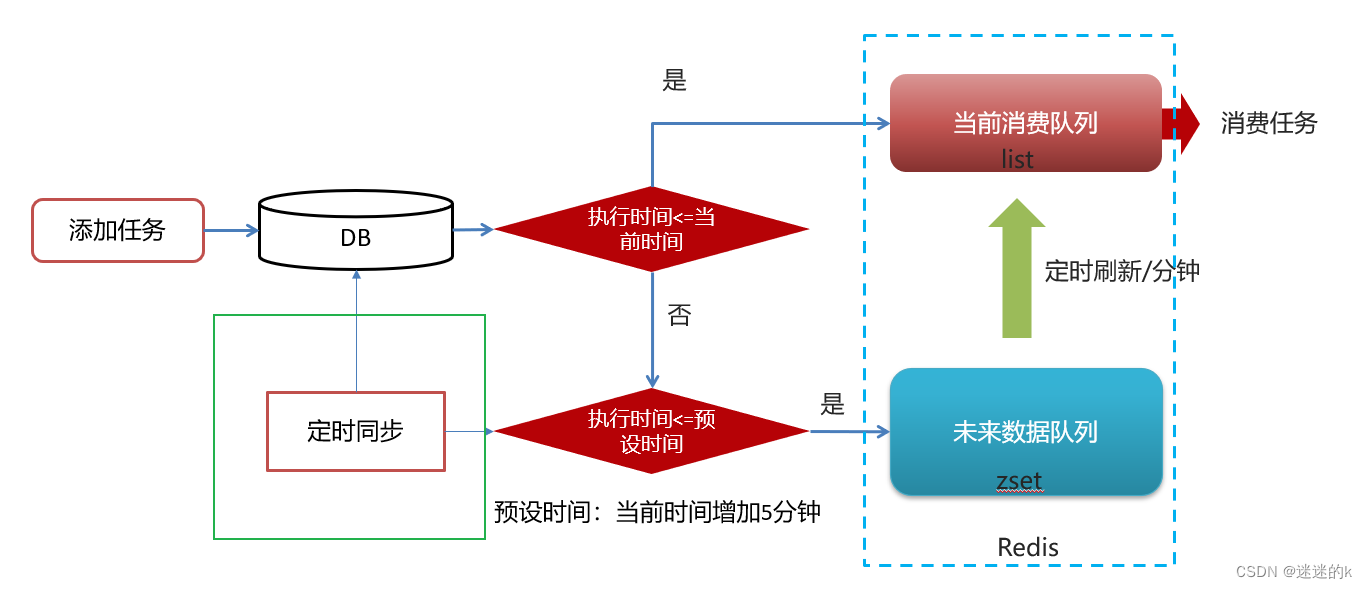
延时任务定时发布,基于 Redis 与 DB 实现
目录 1、什么是延时任务,分别可以使用哪些技术实现? 1.2 使用 Redis 和 DB 相结合的思路图以及分析 2、实现添加任务、取消任务、拉取任务 3、实现未来数据的定时更新 4、将数据库中的任务数据,同步到 Redis 中 1、什么是延时任务ÿ…...

Nacos安装使用
Nacos安装使用 官方下载地址: https://github.com/alibaba/nacos/releases 官方文档地址: https://nacos.io/zh-cn/docs/quick-start.html Nacos介绍 Nacos是阿里巴巴开源的一款支持服务注册与发现,配置管理以及微服务管理的组件。用来取代以前常用的注册中心&a…...
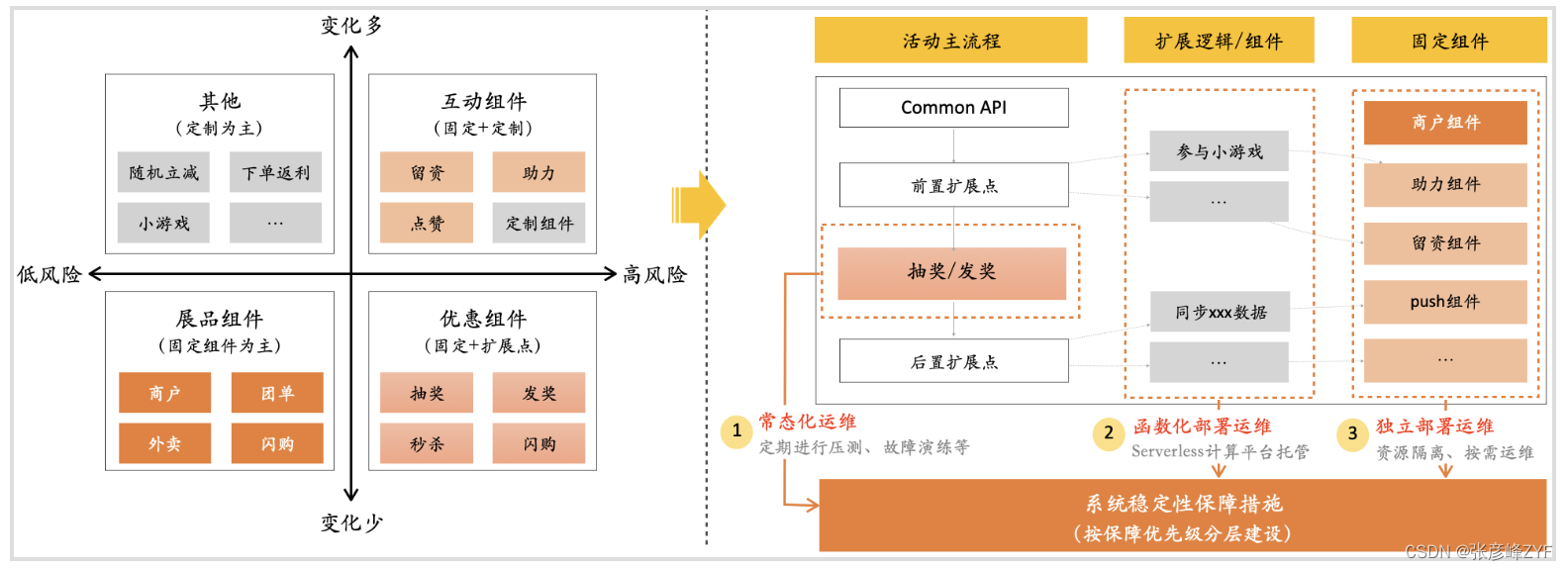
了解抽象思维的应用与实践
目录 一、快速了解抽象思维 (一)抽象思维的本质理解 (二)系统架构中的重要性 (三)软件开发中抽象的基本过程思考 意识和手段 抽象的方式 抽象层次的权衡 二、业务中的应用实践 (一&…...
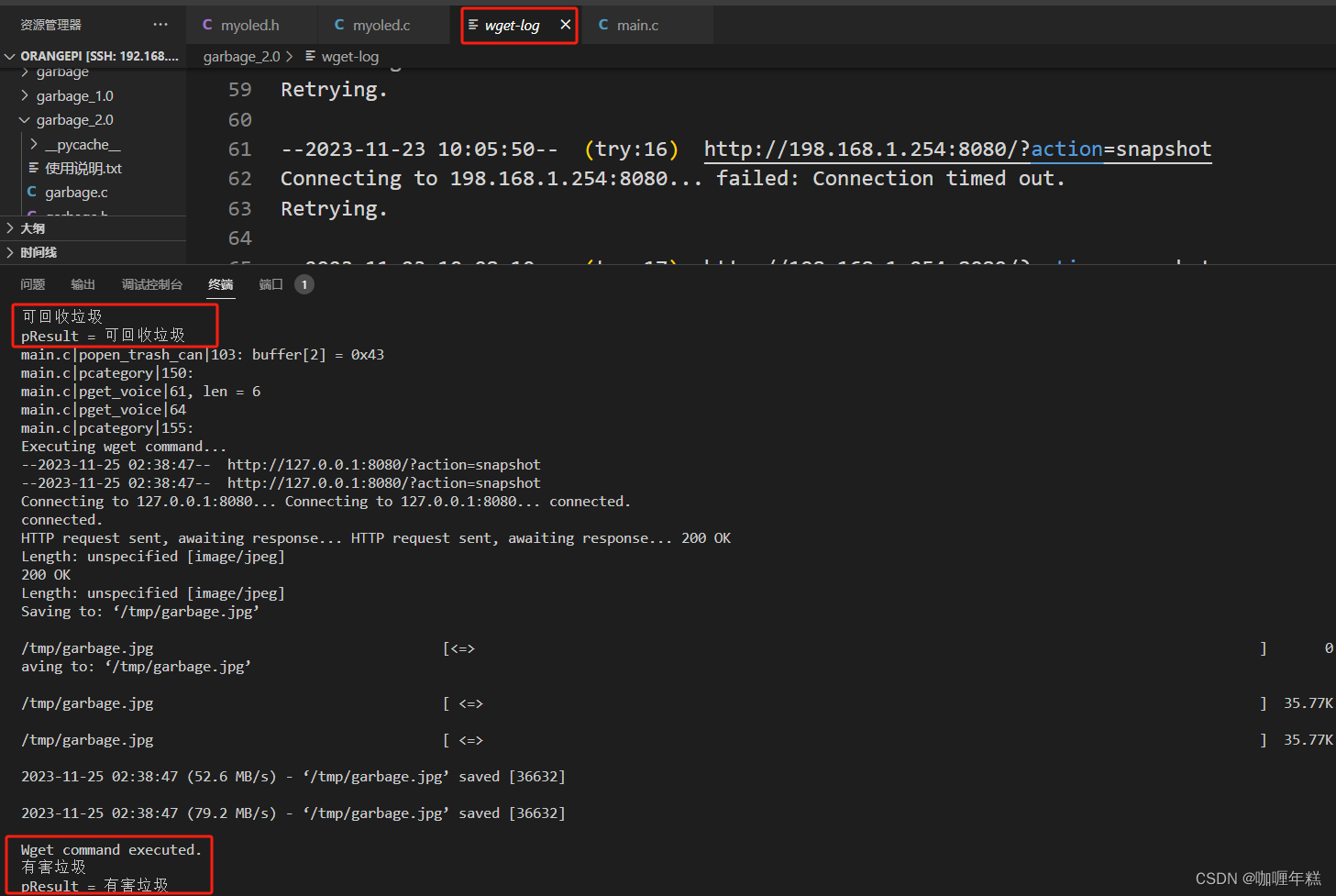
【阿里云】图像识别 智能分类识别 增加垃圾桶开关盖功能点和OLED显示功能点(二)
一、增加垃圾桶开关盖功能 环境准备 二、PWM 频率的公式 三、pthread_detach分离线程,使其在退出时能够自动释放资源 四、具体代码实现 图像识别数据及调试信息wget-log打印日志文件 五、增加OLED显示功能 六、功能点实现语音交互视频 一、增加垃圾桶开关盖功能…...
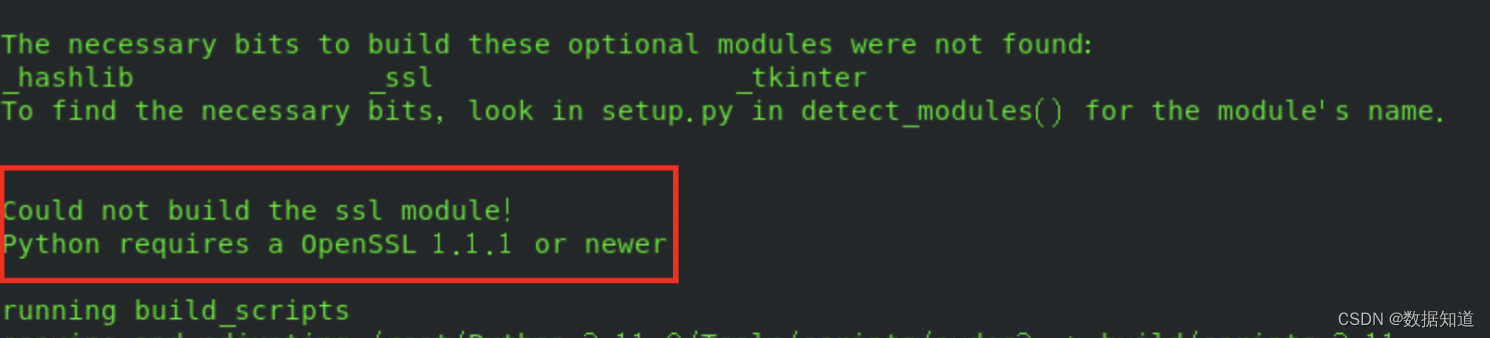
linux centos上安装python3.11.x详细完整教程
一. 安装步骤 注意: 1、安装python3.11的其他版本替换下面的版本信息即可。(如想安装3.11.5将案例中的3.11.0替换成3.11.5即可) #下载最新的软件安装包 wget https://www.python.org/ftp/python/3.11.0/Python-3.11.0.tgz#解压缩安装包 tar -xzf Python-3.11.0.tg…...
itext - PDF模板套打
目录 环境配置 快速使用 代码实现 添加图片 封装 项目需求:获取列表数据之后直接将数据生成一个pdf。因此需要使用到 itext 对pdf进行直接操作。 环境配置 需要为pdf添加文字域,因此需要安装Adobe Acrobat 准备一个空的PDF文件,如果有现…...

指针的使用和传址调用
1.引入 学习指针的⽬的是使⽤指针解决问题,那什么问题,⾮指针不可呢? 例如:写⼀个函数,交换两个整型变量的值。 ⼀番思考后,我们可能写出这样的代码: #include <stdio.h> void Swap1(int…...

【Leetcode】【实现循环队列】【数据结构】
代码实现: typedef struct {int front;int back;int k;int* a;} MyCircularQueue;bool myCircularQueueIsEmpty(MyCircularQueue* obj) {return obj->frontobj->back; }bool myCircularQueueIsFull(MyCircularQueue* obj) {return (obj->back1)%(obj->…...
)
电力感知边缘计算网关产品设计方案-软件架构(业务流程)
软件架构(业务流程) 基于前端系统提供的硬件通信平台,后端系统以控制执行单元为核心,协同控制通信管理、驱动适配、存储单元等职能单元完成与前端系统的通信数据交互业务,在经历以下业务流程后,完成设备自适应通信业务功能。 1.外部设备通信前端系统 前端系统连接新的…...

【labelimg打不开】
labelimg打不开 一、 报错1.1 排除错误 **解决方法:** 一、 报错 当运行labelimg程序报错此条时 AssertionError: Missing string id : useDefaultLabel 1.1 排除错误 第一,进入创建的虚拟环境,输入pip list 查看是否安装了labelimg 第二&…...

JAVA之异常详解
1. 异常的概念与体系结构 1.1 异常的概念 在Java中,将程序执行过程中发生的不正常行为称为异常 1. 算术异常 public class Test {public static void main(String[] args) {System.out.println(10/0);} } 因为 0 不能当被除数,所以报出了异常&#…...
模型优化【2】-剪枝[局部剪枝]
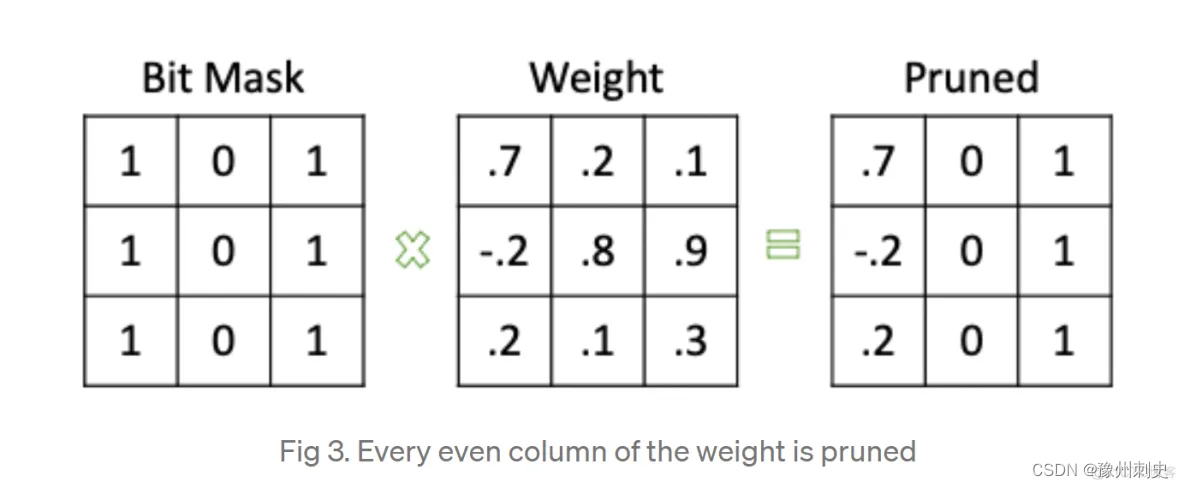
模型剪枝是一种常见的模型压缩技术,它可以通过去除模型中不必要的参数和结构来减小模型的大小和计算量,从而提高模型的效率和速度。在 PyTorch 中,我们可以使用一些库和工具来实现模型剪枝。 pytorch实现剪枝的思路是生成一个掩码࿰…...

VMware 系列:ESXI6.7升级7.0
ESXI6.7升级7.0 一、下载补丁二、上传文件三 启用Shell四、登录Shell后台五、删除不兼容驱动六、正常升级最近,将一台使用ESXI6.7的虚拟机升级到了7.0版本,下面记录一下自己的升级过程。 升级条件 首先确保硬件是否能升级到7.0版本,物理网卡驱动为e1000e不能升级,如果是ig…...
4-20mA高精度采集方案
下载链接!https://mp.weixin.qq.com/s?__bizMzU2OTc4ODA4OA&mid2247557466&idx1&snb5a323285c2629a41d2a896764db27eb&chksmfcfaf28dcb8d7b9bb6211030d9bda53db63ab51f765b4165d9fa630e54301f0406efdabff0fb&token976581939&langzh_CN#rd …...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...
