C++ DAY08 异常
概念
int main(int argc, char *argv[])
{int num = 10 / 0;cout << "OVER" << endl;return 0;
}
//不会显示OVER,程序异常结束抛出异常
语法:throw 值或变量;
例如:
捕获异常
语法:
示例
#include <iostream>
#include <cstring>
using namespace std;
//异常步骤,抛出异常,捕获异常
int mydiv(int a,int b)
{if(b == 0){// 抛出异常int num = 0;throw num;}return a / b;
}
void test01(){try{mydiv(10,0);}catch(int e){cout << e << endl;}catch(char const* s){cout << s << endl;}catch(...){cout << "其他异常" << endl;}
}
int main(int argc, char *argv[])
{test01();return 0;
}栈解旋
概念
示例
class A{
private:
int num;
public:
A(int num):num(num)
{cout << "构造函数" << num << endl;
}
~A()
{cout << "析构函数" << num << endl;
}
};
void test02()
{A a1(1);A a2(2);throw 0;
}
int main(int argc, char *argv[])
{try{test02();}catch(...){}return 0;
}结果
异常的接口声明
作用
语法
示例
void fun01()throw(int,char)
{// throw 10;//可以// throw 'a';//可以// throw 3.14f;//不可以
}
void test03(){try{fun01();}catch(int){cout << "int的异常" << endl;}catch(char){cout << "char的异常" << endl;}catch(float){cout << "float的异常" << endl;}
}
int main(int argc, char *argv[])
{test03();return 0;
}异常对象的生命周期
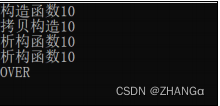
示例1:抛出异常对象
#include <iostream>
#include <cstring>
using namespace std;
class B{
private:int num;
public:B(int num):num(num){cout << "构造函数" << num << endl;}B(const B& b){this->num = b.num;cout << "拷贝构造" << num << endl;}~B(){cout << "析构函数" << num << endl;}
};
void fun02()
{throw B(10);
}
void test04()
{try{fun02();}catch(B b){}
}
int main(int argc, char *argv[])
{test04();cout << "OVER" << endl;return 0;
}结果
示例2:抛出异常对象指针
#include <iostream>
#include <cstring>
using namespace std;
class B{
private:int num;
public:B(int num):num(num){cout << "构造函数" << num << endl;}B(const B& b){this->num = b.num;cout << "拷贝构造" << num << endl;}~B(){cout << "析构函数" << num << endl;}
};
void fun02()
{throw new B(10);
}
void test04()
{try{fun02();}catch(B *b){}
}
int main(int argc, char *argv[])
{test04();cout << "OVER" << endl;return 0;
}结果:
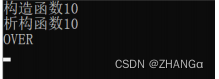
示例3:抛出异常对象引用
#include <iostream>
#include <cstring>
using namespace std;
class B{
private:int num;
public:B(int num):num(num){cout << "构造函数" << num << endl;}B(const B& b){this->num = b.num;cout << "拷贝构造" << num << endl;}~B(){cout << "析构函数" << num << endl;}
};
void fun02()
{throw B(10);
}
void test04()
{try{fun02();}catch(B &b){}
}
int main(int argc, char *argv[])
{test04();cout << "OVER" << endl;return 0;
}结果:
异常的多态
class BaseException{};
class MyException01:public BaseException{};
class MyException02:public BaseException{};
void test05()
{try{throw MyException01();}catch(BaseException){cout << "可以捕获子类异常" << endl;}
}
int main(int argc, char *argv[])
{test05();return 0;
}class BaseException{
public:virtual void printMsg(){}
};
class NullException:public BaseException{
public:virtual void printMsg(){cout << "空指针异常" << endl;}
};
class ArrOutException:public BaseException{
public:virtual void printMsg(){cout << "数组下标越界异常" << endl;}
};
void test05()
{try{throw NullException();}catch(BaseException &e){e.printMsg();}
}
int main(int argc, char *argv[])
{test05();return 0;
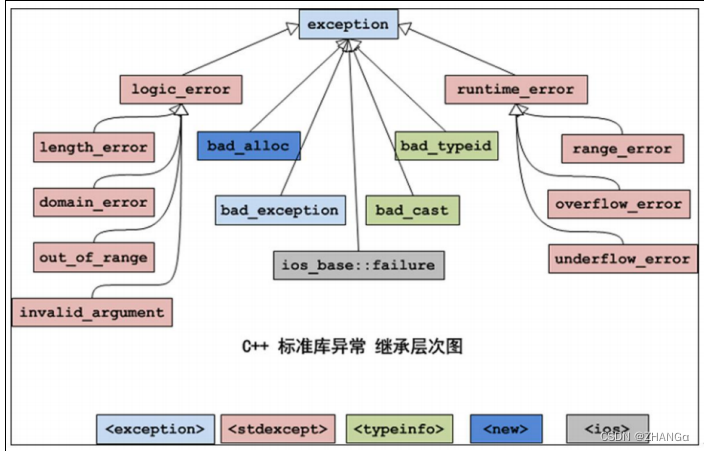
}标准异常库
简介
标准异常使用
void test06()
{try{throw bad_alloc();}catch(exception &e){cout << e.what() << endl;}
}
int main(int argc, char *argv[])
{test06();return 0;
}自定义异常
步骤
示例
class my_exception:public exception
{
private:char* msg;
public:my_exception(){}my_exception(char* msg){this->msg = msg;}const char *what()const noexcept{return msg;}
};
void test07()
{try{throw my_exception("自定义异常");}catch(exception &e){cout << e.what() << endl;}
}
int main(int argc, char *argv[])
{test07();return 0;
}相关文章:

C++ DAY08 异常
概念 异常事件(如:除 0 溢出,数组下标越界,所要读取的文件不存在 , 空指针,内存不足 等等) 在 C 语言对错误的处理是两种方法: 一是使用整型的返回值标识错误; 二是使用 errn…...

vscode导入STM32CubeIDE工程文件夹未定义警告清除方法
0 前言 在我们使用vscode去编辑STM32CubeIDE的工程文件时,经常会出现一些类型未定义、头文件路径无效的问题,无法正常使用且非常影响观感。本文介绍如何设置vscode导入的STM32CubeIDE配置文件,解决这一问题。 1 vscode导入STM32CubeIDE工程…...
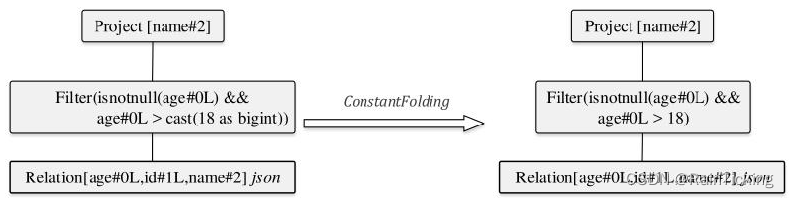
SparkSQL之Optimized LogicalPlan生成过程
经过Analyzer的处理,Unresolved LogicalPlan已经解析成为Analyzed LogicalPlan。Analyzed LogicalPlan中自底向上节点分别对应Relation、Subquery、Filter和Project算子。 Analyzed LogicalPlan基本上是根据Unresolved LogicalPlan一对一转换过来的,…...
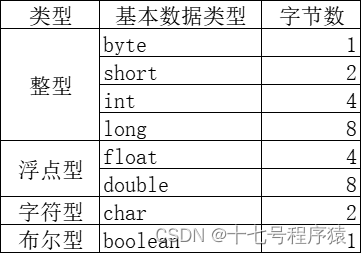
Java中有几种基本数据类型以及转换方式【Java面经(1)】
问:Java中有几种基本数据类型呢?以及它们之间的转换方式。详细介绍下 总共有8种基本数据类型 byte 、short 、long 、float 、double 、boolean 、char 详细类型以及字节数: 基本数据类型的转换方式 自动类型转换:小–>大 byt…...

JVM虚拟机:JVM调优第一步,了解JVM常用命令行参数
本文重点 从本文课程开始,我们将用几篇文章来介绍JVM中常用的命令行的参数,这个非常重要,第一我们可以通过参数了解JVM的配置,第二我们可以通过参数完成对JVM的调参。以及后面的JVM的调优也需要用到这些参数,所以我们…...

CSS特效019:图标图片悬浮旋转一周
CSS常用示例100专栏目录 本专栏记录的是经常使用的CSS示例与技巧,主要包含CSS布局,CSS特效,CSS花边信息三部分内容。其中CSS布局主要是列出一些常用的CSS布局信息点,CSS特效主要是一些动画示例,CSS花边是描述了一些CSS…...

requests请求django接口跨域问题处理
参考: https://zhuanlan.zhihu.com/p/416978320 https://blog.csdn.net/SweetHeartHuaZai/article/details/130983179 使用httpx代替requests import httpxheaders {"User-Agent": "Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.3…...

#Js篇:Promise
定义 Promise是异步操作解决方案,为异步操作提供统一接口。 Promise英文意思是“承诺”,表示其他手段无法改变。 返回 所有异步任务都返回一个Promise实例。 Promise实例有一个then方法,用于指定下一步的回调函数。 状态 异步操作未完…...
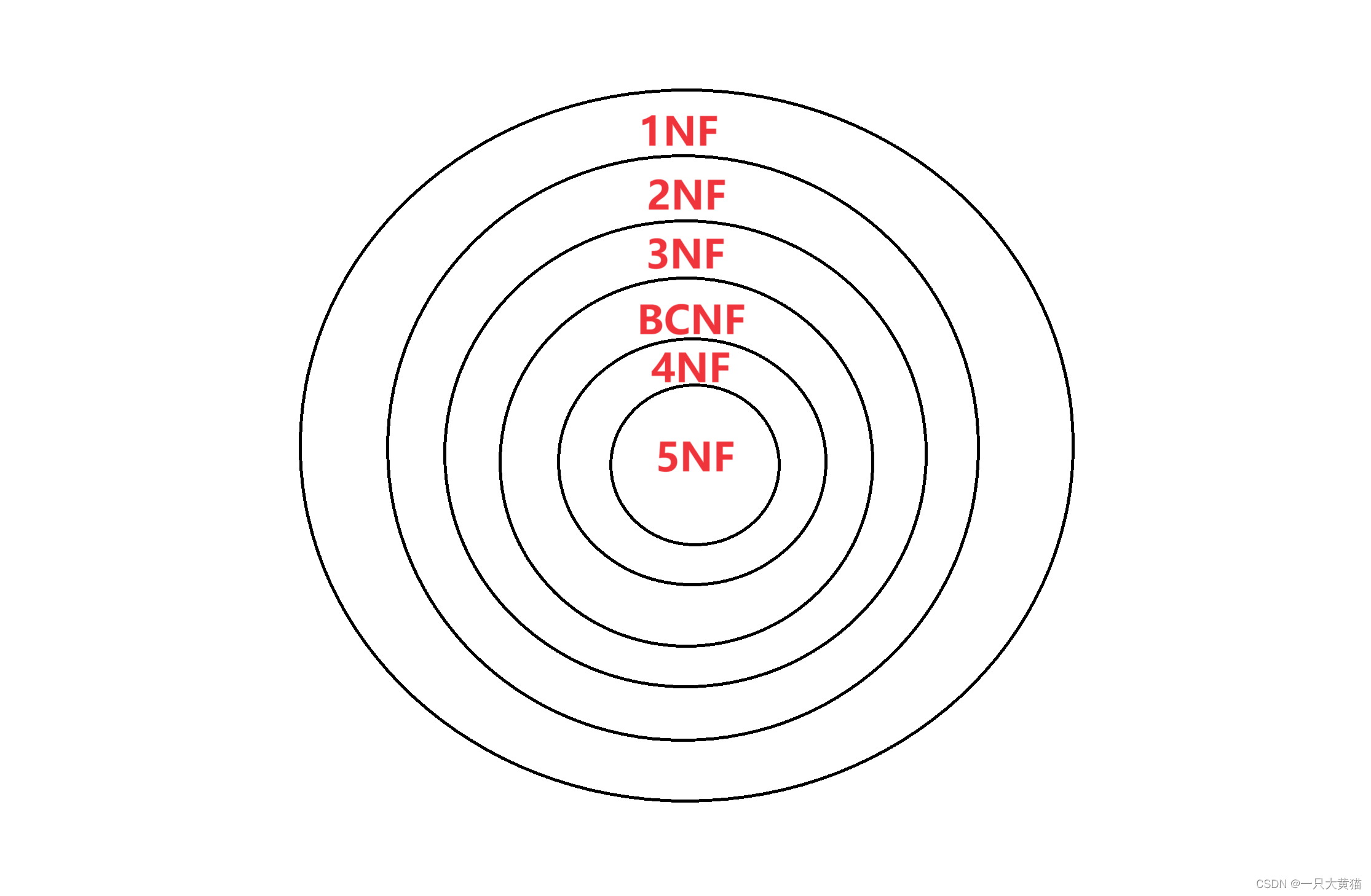
【数据库篇】关系模式的表示——(2)规范化
范式:范式是符合某一种级别的关系模式的集合 规范化:是指一个低一级的范式的关系模式,通过模式的分解转换为若干个高一级范式的关系模式的集合。 1NF 每个分量必须是不可分开的数据项,满足这个条件的关系模式就是1NF。 2NF 若…...

【C++那些事儿】类与对象(3)
君兮_的个人主页 即使走的再远,也勿忘启程时的初心 C/C 游戏开发 Hello,米娜桑们,这里是君兮_,我之前看过一套书叫做《明朝那些事儿》,把本来枯燥的历史讲的生动有趣。而C作为一门接近底层的语言,无疑是抽象且难度颇…...

spark的算子
spark的算子 1.spark的单Value算子 Spark中的单Value算子是指对一个RDD中的每个元素进行操作,并返回一个新的RDD。下面详细介绍一些常用的单Value算子及其功能: map:逐条映射,将RDD中的每个元素通过指定的函数转换成另一个值&am…...

【科技素养】蓝桥杯STEMA 科技素养组模拟练习试卷7
1、一袋小球中有15个白球,3个红球和2个黑球。在随机从袋子中拿出至少()个小球后,才可以保证至少拿出了5个白球 A、5 B、10 C、8 D、15 答案:B 2、以下选项中,数值最接近十进制数114的是( &…...
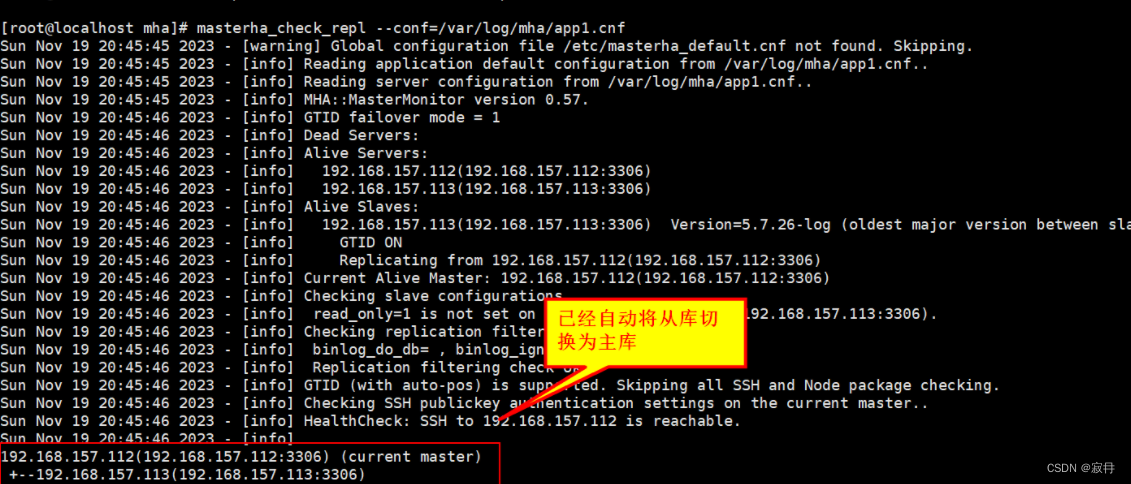
MySQL MHA高可用架构搭建
快捷查看指令 ctrlf 进行搜索会直接定位到需要的知识点和命令讲解(如有不正确的地方欢迎各位小伙伴在评论区提意见,博主会及时修改) MySQL MHA高可用架构搭建 MHA(Master HA)是一款开源的 MySQL 的高可用程序…...

UE小计:顶部工具栏按钮添加下拉列表,大纲列表、资源管理窗口右键添加按键
下拉列表 void FYouPluginsModule::StartupModule() {FYouToolStyle::Initialize();FYouToolStyle::ReloadTextures();FYouToolCommands::Register();PluginCommands MakeShareable(new FUICommandList);PluginCommands->MapAction(FYouToolCommands::Get().PackByCloudAc…...
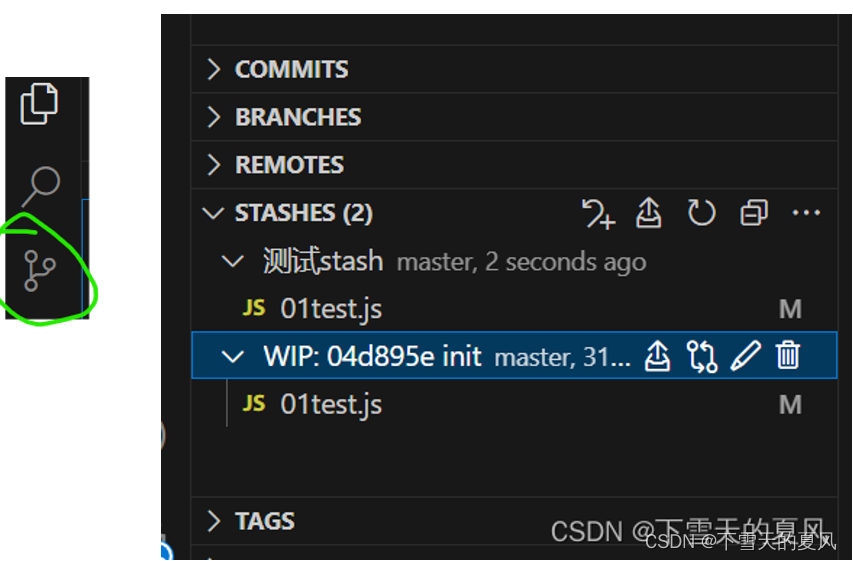
git stash 用法总结
目录 1,介绍场景1:场景2: 2,常用命令2.1,基础2.2,进阶1,存储时指定备注2,通过索引来操作指定的存储3,修改存储规则 2.3,查看 stash 修改的具体内容 1…...
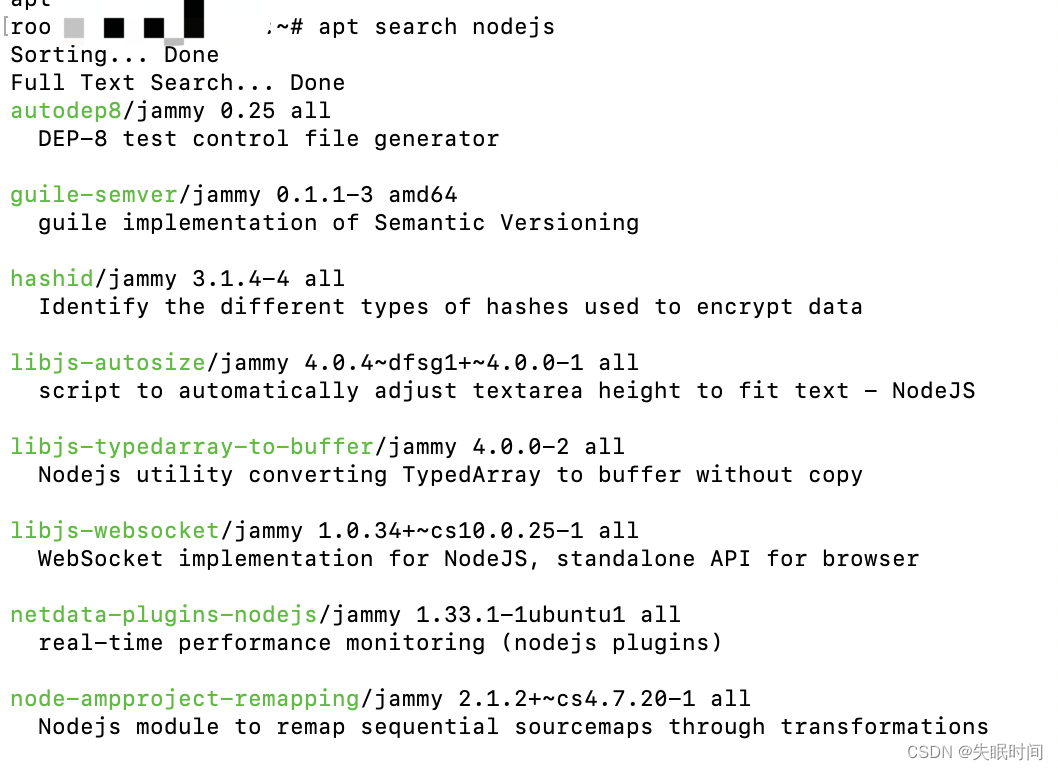
Linux操作系统之apt常用命令记录
文章目录 apt 命令apt 语法apt 常用命令列出所有可更新的软件清单命令升级软件包列出可更新的软件包及版本信息升级软件包,升级前先删除需要更新软件包安装指定的软件命令:安装多个软件包:更新指定的软件命令显示软件包具体信息,例如…...
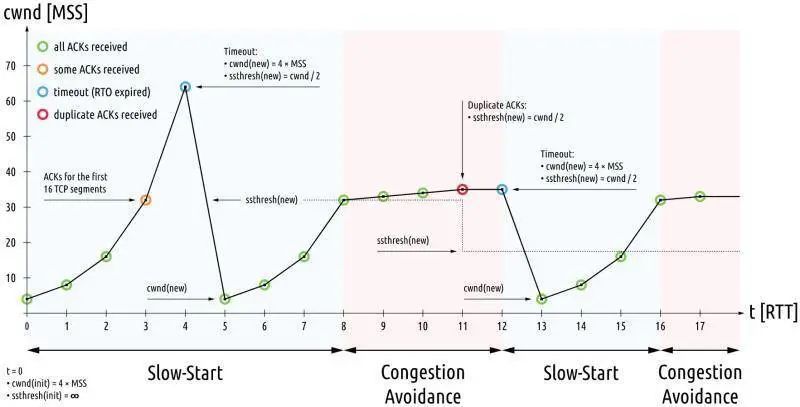
TCP 重传、滑动窗口、流量控制、拥塞控制的剖析
TCP 是一个可靠传输的协议,那它是如何保证可靠的呢? 为了实现可靠性传输,需要考虑很多事情,例如数据的破坏、丢包、重复以及分片顺序混乱等问题。如不能解决这些问题,也就无从谈起可靠传输。 那么,TCP 是…...
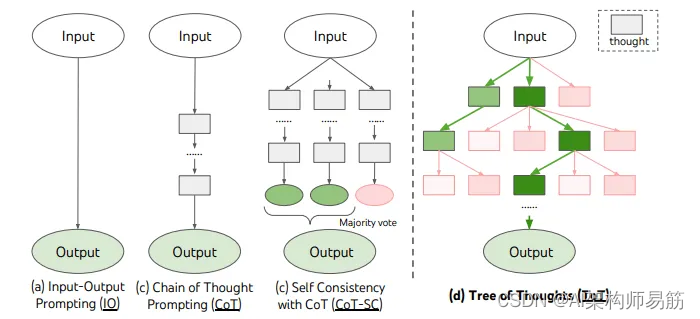
LangChain 11实现思维树Implementing the Tree of Thoughts in LangChain’s Chain
思维之树( Tree of Thoughts ToT)是一个算法,它结合了普林斯顿大学和谷歌DeepMind在本文中提出的大型语言模型(LLMs)和启发式搜索。看起来这个算法正在被实现到谷歌正在开发的多模式生成AI Gemini中。 现在࿰…...

Drools 7 Modify 和对象直接赋值差异
modify代表修改fact,会再次触发符合条件的rule对象直接修改只是java 操作,不会会再次触发符合条件的rule 以下为测试代码-drl部分 package org.drools.learnimport org.drools.learn.ModifyTest.Message;global java.util.List listrule "Stateles…...
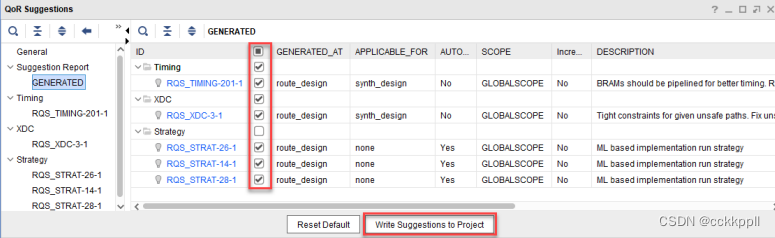
vivado产生报告阅读分析21
其他命令选项 • -of_objects <suggestion objects> : 启用特定建议的报告。在此模式下运行时 , report_qor_suggestions 不会生成新建议。此命令可快速执行 , 读取 RQS 文件后 , 此命令可用于查看其中包 含的建议。其…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

前端调试HTTP状态码
1xx(信息类状态码) 这类状态码表示临时响应,需要客户端继续处理请求。 100 Continue 服务器已收到请求的初始部分,客户端应继续发送剩余部分。 2xx(成功类状态码) 表示请求已成功被服务器接收、理解并处…...

小智AI+MCP
什么是小智AI和MCP 如果还不清楚的先看往期文章 手搓小智AI聊天机器人 MCP 深度解析:AI 的USB接口 如何使用小智MCP 1.刷支持mcp的小智固件 2.下载官方MCP的示例代码 Github:https://github.com/78/mcp-calculator 安这个步骤执行 其中MCP_ENDPOI…...

渗透实战PortSwigger Labs指南:自定义标签XSS和SVG XSS利用
阻止除自定义标签之外的所有标签 先输入一些标签测试,说是全部标签都被禁了 除了自定义的 自定义<my-tag onmouseoveralert(xss)> <my-tag idx onfocusalert(document.cookie) tabindex1> onfocus 当元素获得焦点时(如通过点击或键盘导航&…...
