移动机器人路径规划(七)--- 基于MDP的路径规划MDP-Based Planning
目录
1 什么是MDP-Based Planning
2 worst-case analysis for nondeterministic model
3 Expected Cost Planning
4 Real Time Dynamic Programming(RTDP)
1 什么是MDP-Based Planning
之前我们从起点到终点存在很多可执行路径,我们可以通过执行的时候根据环境的变化去选择最优的路径。
到目前为止,我们假设机器人是在理想情况下进行的planning(机器人的执行是完美的、机器人的估计是完美的)。
用上面两幅图说,我们规划一个地点到另一个地点的路线,我们假设让机器人走一个格子它就走一个格子。右图的话我们假设精准的反映环境的情况,估计好位姿以后,假设机器人精准的到了终点的位姿不存在意外情况。
实际并非如此:
当在实际应用中,执行和状态估计都不是完美的。
• 执行不确定性:打滑、崎岖地形、风、空气阻力、控制误差等。
• 状态估计不确定性:传感器噪声、校准误差、不完美估计、部分可观测性等。
不确定性可以从机器人的视角分为两类,这表明机器人可以利用多少信息。
不确定性模型
• 非确定性:机器人不知道会有什么类型的不确定性或干扰被添加到其行为(下一步动作)中。(偏移目标点非常远受自然环境影响)
• 概率性:机器人通过观察和收集统计数据对不确定性有一定估计。(运行一部分后直到自己受干扰程度)
为了正式描述这个概念,我们首先引入两个决策者来模拟不确定性的产生,然后是带有不确定性的规划类型。
决策者(游戏参与者):
• 机器人是主要的决策者,根据完全已知的状态和完美执行进行规划。
• 自然界向机器人制定的计划添加不确定性,这对机器人来说是不可预测的。
Formalization-7.1:与自然界的博弈(独立博弈)
• 非空集合 U 称为机器人行动空间(robot action space)。每个 u ∈ U 被称为机器人行动。
• 非空集合 Θ 称为自然界行动空间(nature action space)。每个 θ ∈ Θ 被称为自然界行动。
• 函数 L:U × Θ → R ∪ {∞},称为成本函数(cost function)或负奖励函数。Formalization-7.2:自然界了解机器人行动(依赖博弈)
• 非空集合 U 称为机器人行动空间。每个 u ∈ U 被称为机器人行动。
• 对于每个 u ∈ U,有一个非空集合 Θ(u) 称为自然界行动空间。
• 函数 L:U × Θ → R ∪ {∞},称为成本函数或负奖励函数。
在机器人与自然界进行博弈时,对机器人来说什么是最佳决策?一步最坏情况分析(One-step Worst-Case Analysis)
• 在非确定性(Nondeterministic)模型下,独立博弈中的 P(θ) 和依赖博弈中的 P(θ|u_k) 是未知的;
• 机器人无法预测自然界的行为,并假设它恶意地选择会使成本尽可能高的行动;
• 因此,假设最坏情况下做出决策是合理的。
我们穷举所有的nature action space,从中筛选出最不利的这种情况让机器人执行这个动作将最不利降到最低。
• 在概率模型下,独立博弈中的 P(θ) 和依赖博弈中的 P(θ|u_k) 是已知的;
• 假设已经观察到了应用的自然界行动,并且自然界在选择行动时采用了随机化策略。
• 因此,我们优化获得平均成本(average cost to be received)。
机器人每执行一个动作,环境会对齐施加各种影响,我们去求一下各种影响的期望选择让期望值最小的一个动作。
多步的情况下呢?
Formalization-7.2:带有自然界的离散规划
1. 具有初始状态 x_s 和目标集合 X_F ⊂ X 的非空状态空间 X。
2. 对于每个状态 x ∈ X,有一个有限且非空的机器人行动空间 U(x)。对于每个 x ∈ X 和 u ∈ U(x),有一个有限且非空的自然界行动空间 Θ(x, u)。
3.状态转移函数 f (x, u, θ) 对于每个 x ∈ X, u ∈ U,和 θ ∈ Θ(x, u):
4.一组阶段(机器人不由但一阶段表示),每个阶段用 k 表示,从 k = 1 开始并无限持续,或者在最大阶段 k = K + 1 = F 结束。
5.一个阶段叠加的成本函数 L。让 x̃ F,ũ k,θ̃ K 表示截止到第 K 阶段的状态历史、机器人行动和自然界行动:
马尔可夫决策过程(MDP)
在学习领域,MDP 是一个 4 元组 (S, A, P, R),在规划领域则是 (X, U, P, L):
• S 或 X 是状态空间,
• A 或 U 是(机器人)动作空间,
• P(x_k+1 |x_k, u_k) 是概率模型下的状态转移函数,在非确定性模型下退化为一个集合 X_k+1 (x_k, u_k),
• R(x_k, x_k+1) 是即时奖励,或者是由于 u、θ 从 x_k 过渡到 x_k+1 的负一步成本 −l(x_k, u_k, θ_k)。
面对不确定性进行规划的第一个难题在于用 MDP 模型适当地形式化我们的问题。
机器人从
移动到
,状态空间就是布满黑点的区域。动作空间就是五种(停留在原地、上下左右)。
nature的动作空间:
1.我们假定机器人在
这个位置执行了
动作含一个随机的高斯误差。(连续)
2.对nature的动作空间进行离散化的定义,机器人在
这个位置执行了
动作加上一个额外的动作。(离散)
代价函数l:下一个状态与当前状态的距离差。
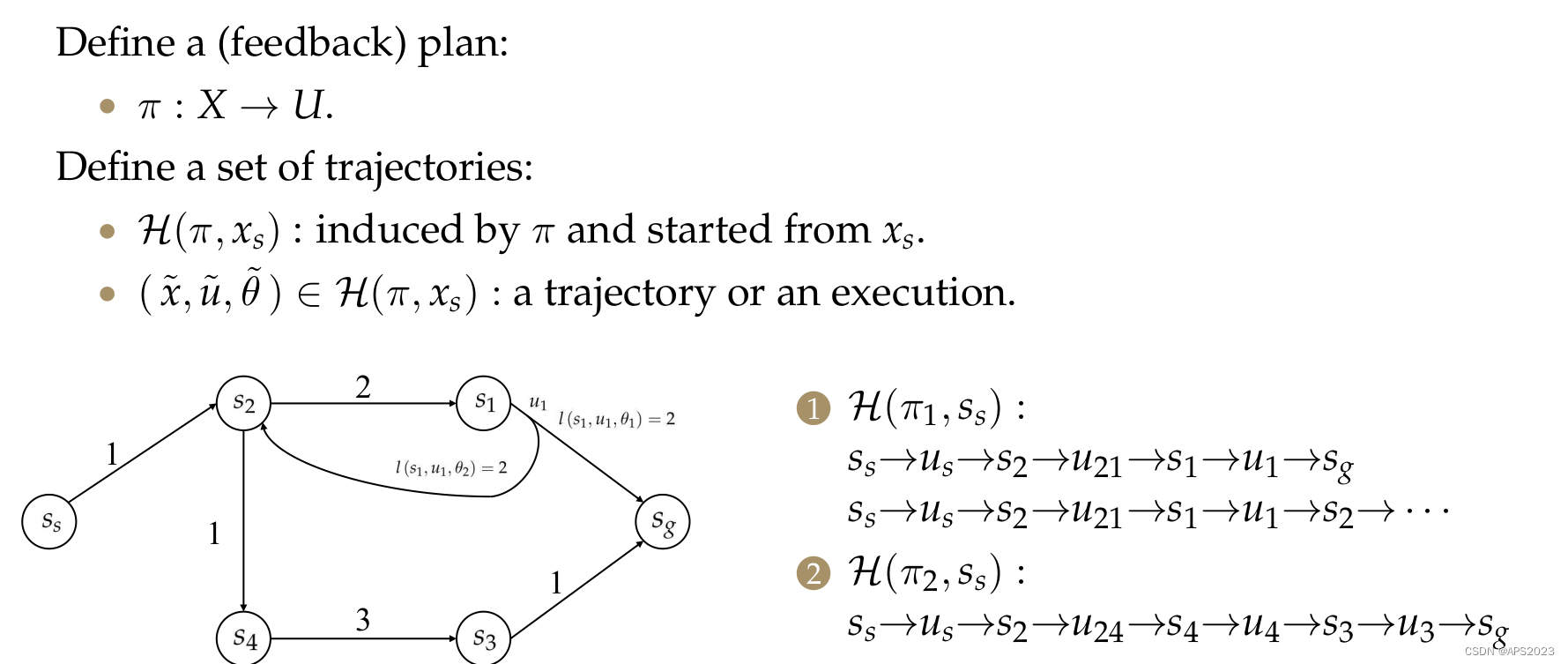
我们希望找一个路径(以最小的代价移动到目标位置)。
是状态空间到动作空间的一个映射,它规定了在什么状态下我应该执行一个什么样的动作,是一个离散集合的形式。
定义衡量policy好坏的变量:
33
2 worst-case analysis for nondeterministic model
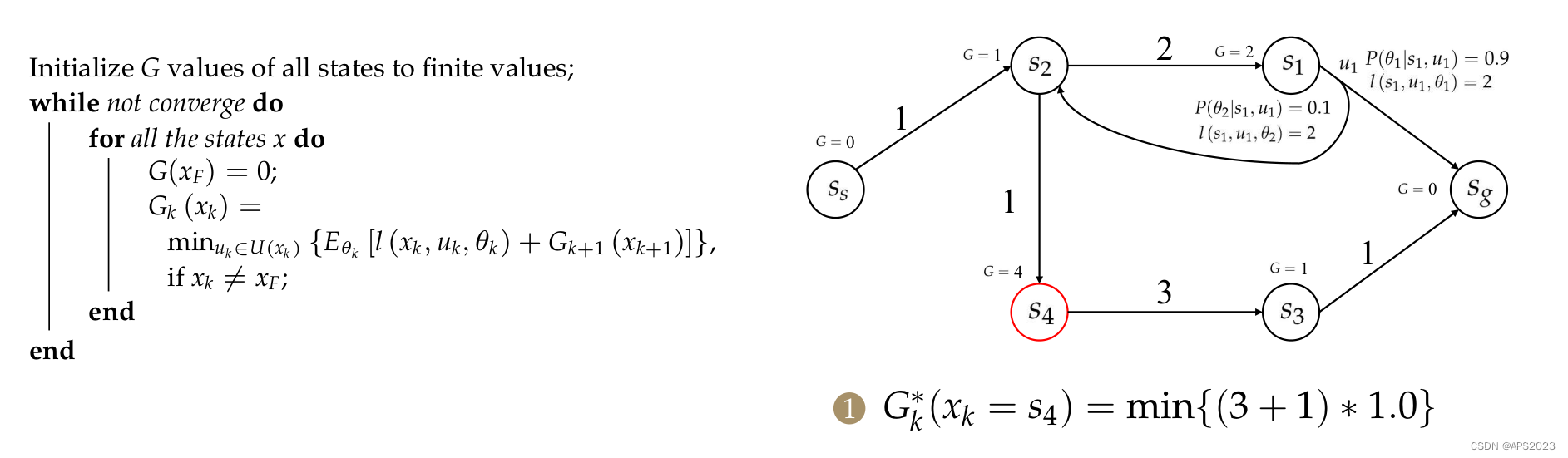
我们拿一个具体的例子:
第K+1步最优的cost to go已经知道了,我们现在在当前状态
机器人执行了特征的动作
,机器人能从这个
转移到具体的哪个
是由
决定的。我们找一个
使得单步的cost加上K+1的cost to go和最大的
,我们再去选择cost最小的
。
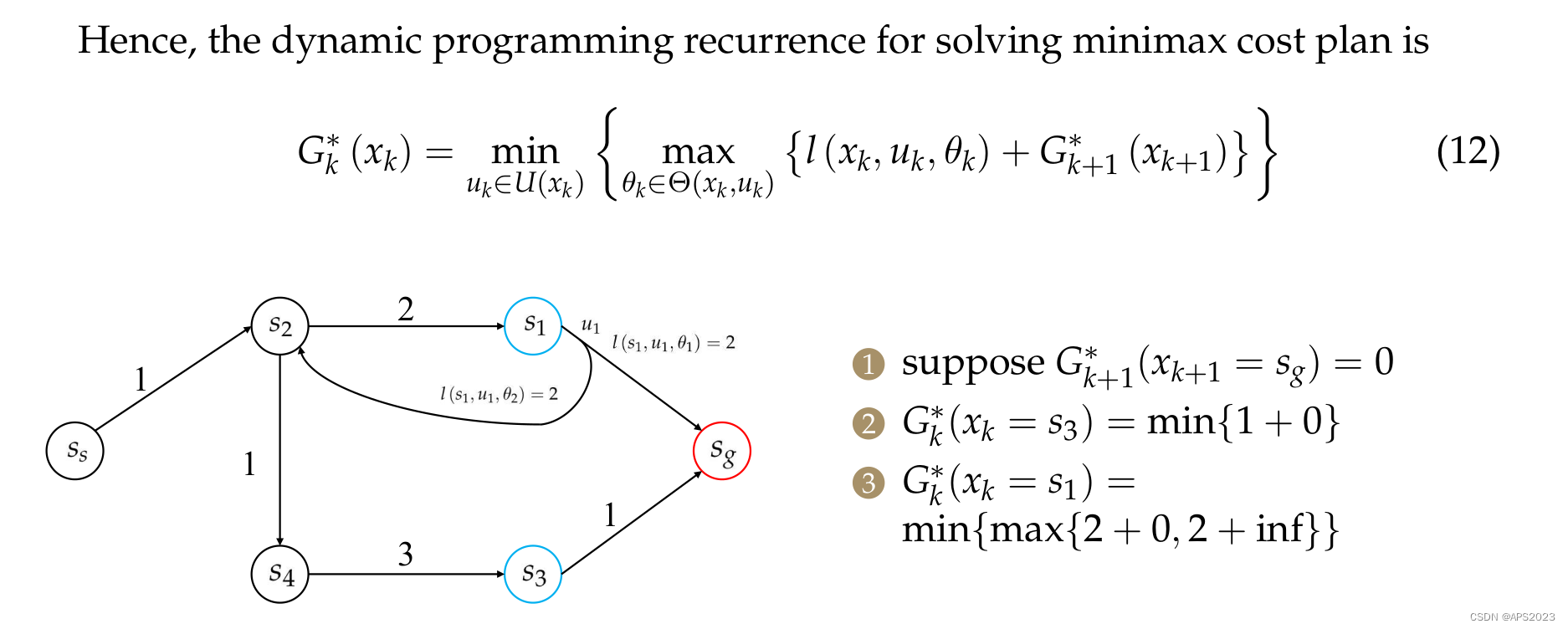
我们假设终点处的cost to go是0,其他地方未知。S3来说,cost to go为0+1。s1来说,只有一个u,但是有两个
,一个是单步2 + 终点0,另一个分支的话 2 + s2的cost to go(还未计算)。
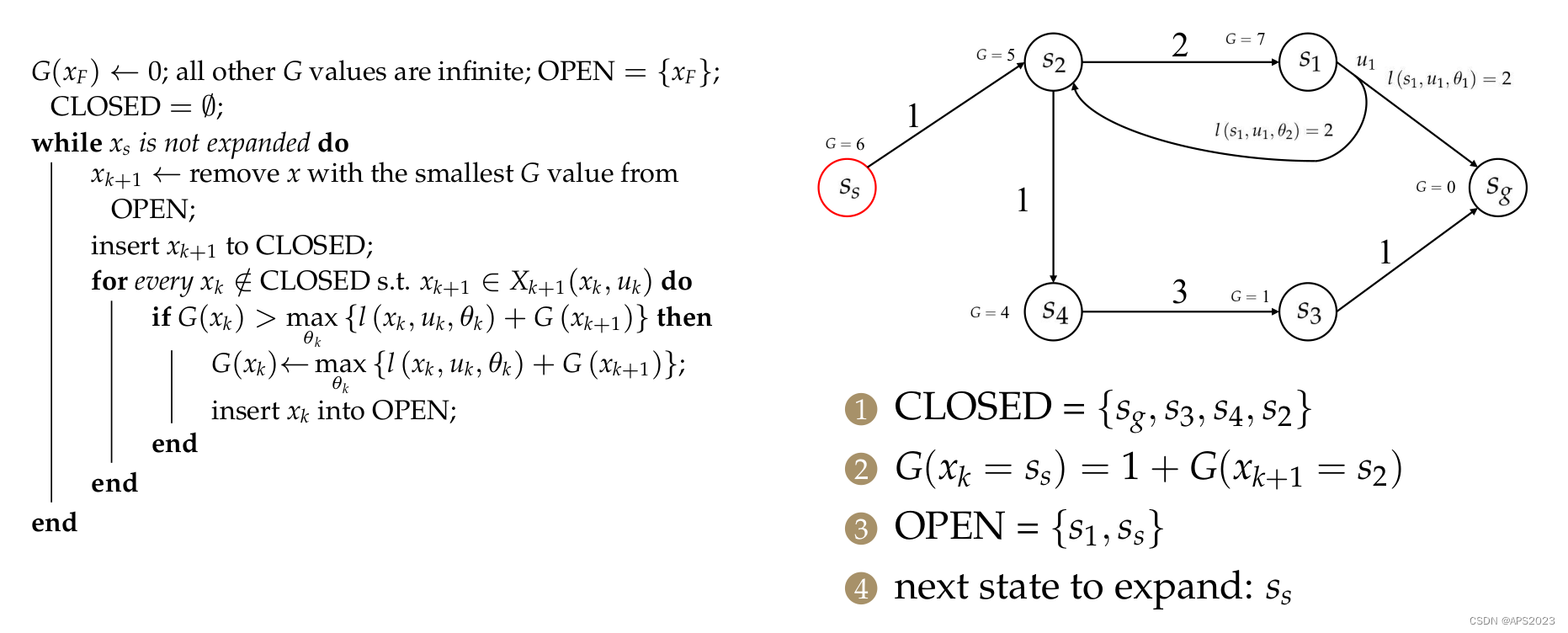
从终点到起点迭代求解。
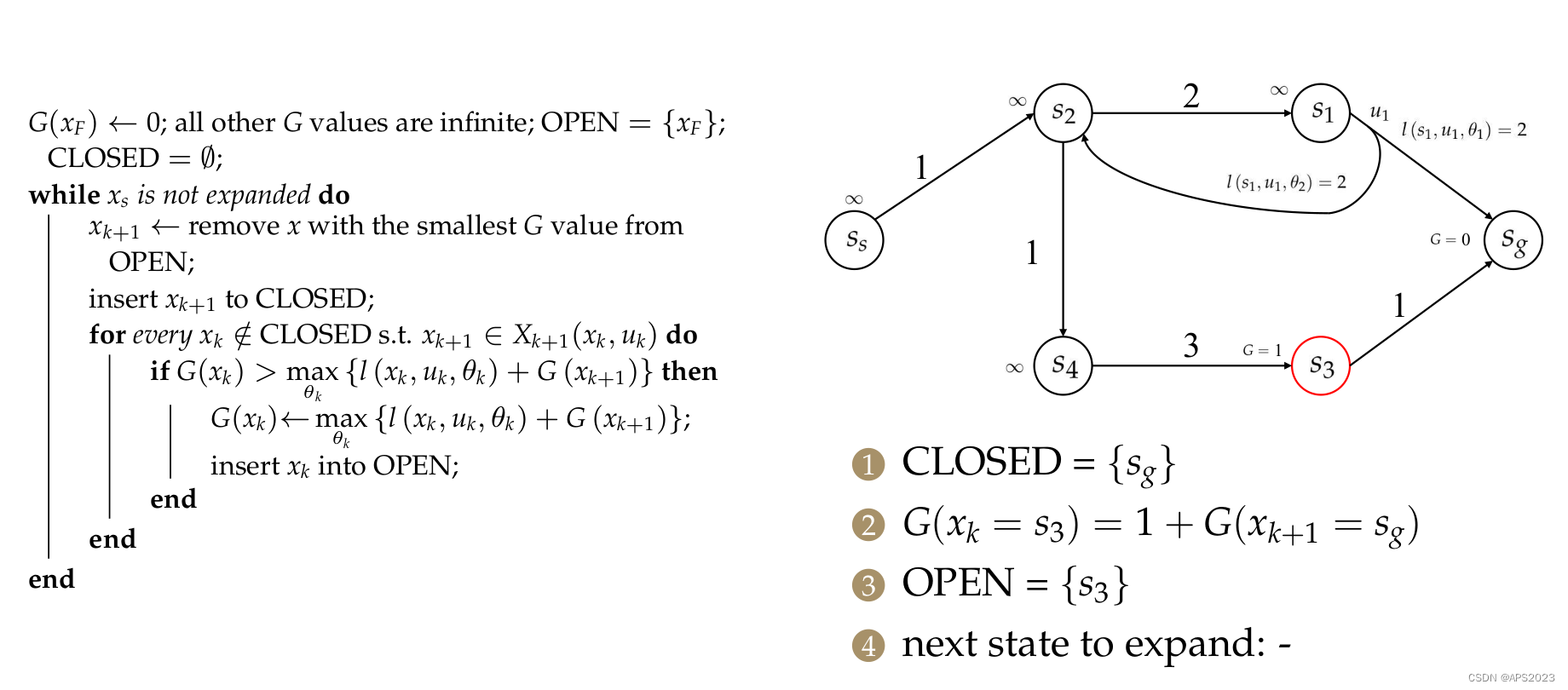
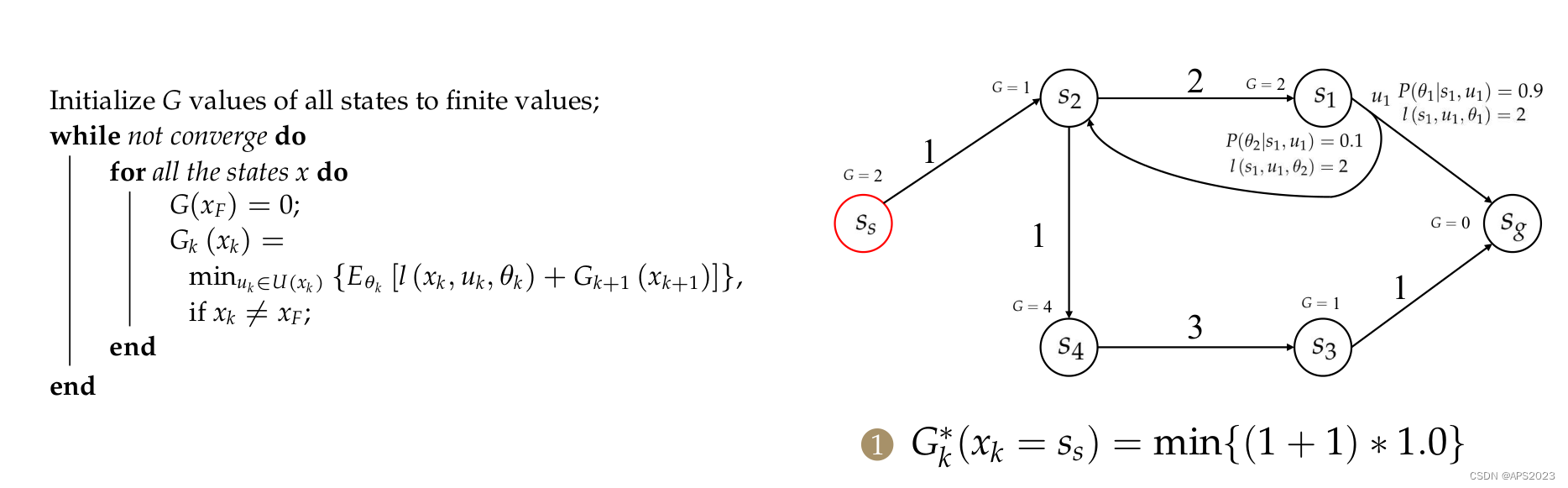
举一个例子:
首先我们将
,其他的设置为无穷,将openlist初始化为
。
下一次待扩展状态为
。下一步找其前继节点。
对于
,计算
,openlist添加
。
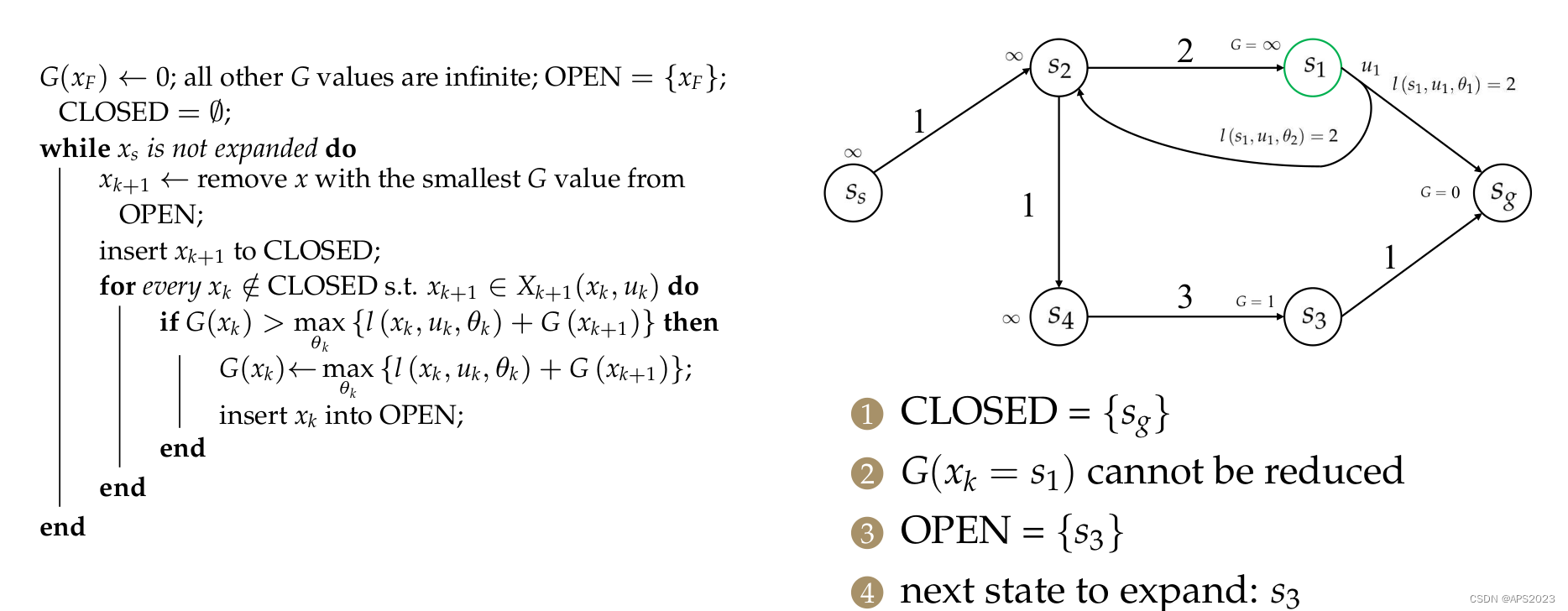
对于
,
(inf.....不能更新,无法放入openlist),
。
对于s4,相同的。
对于s2,也是相同的。不过它有两个前继节点
。先对S1进行处理:
最后更新Ss:
优点、缺点:
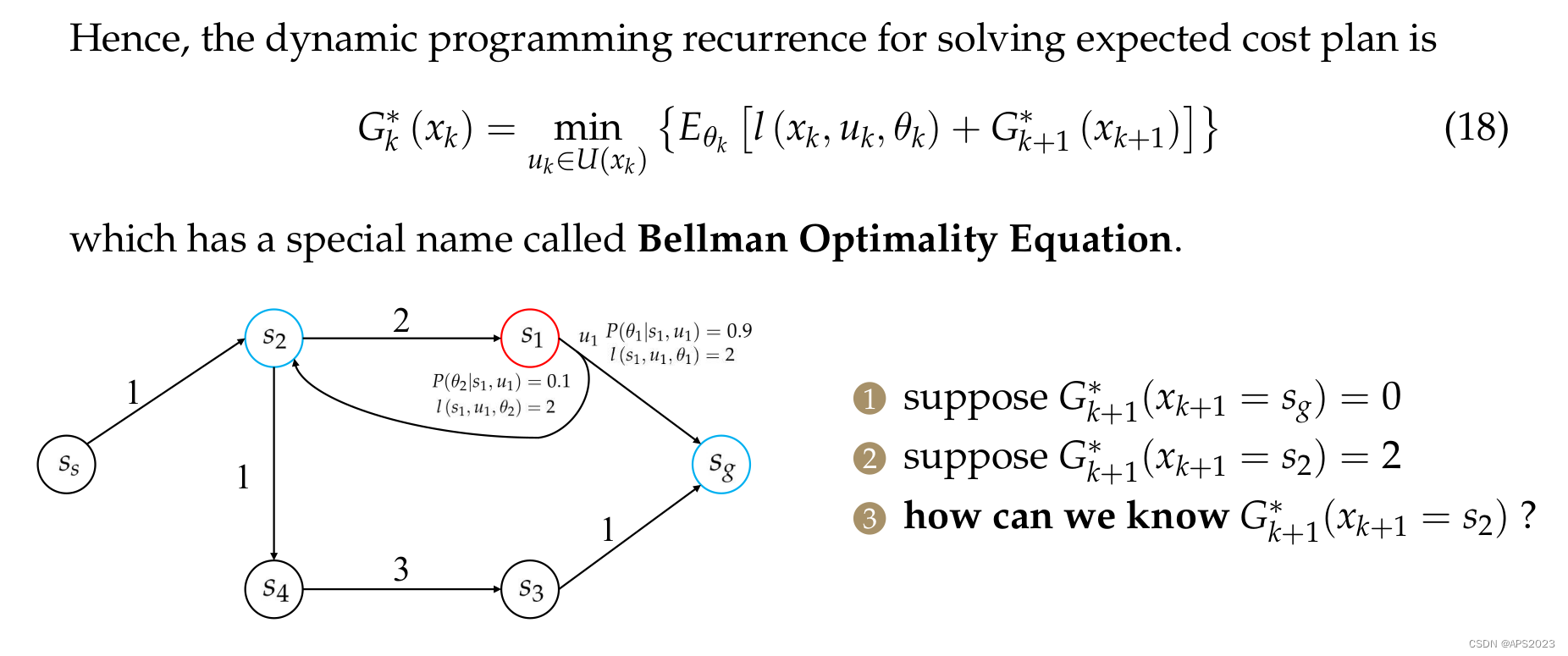
3 Expected Cost Planning
那么问题来了?
我们来看算法描述:
举个例子把:
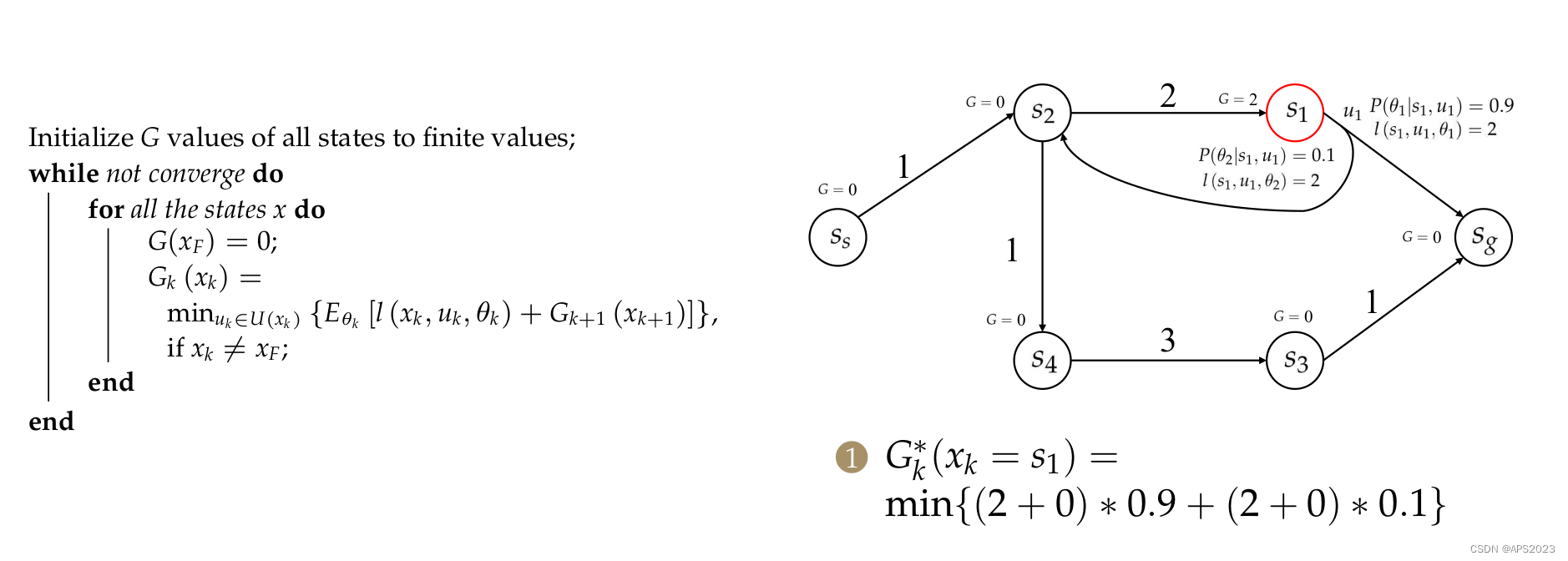
首先我们把
初始化为0。选择一个迭代顺序
。
先来看
的更新:
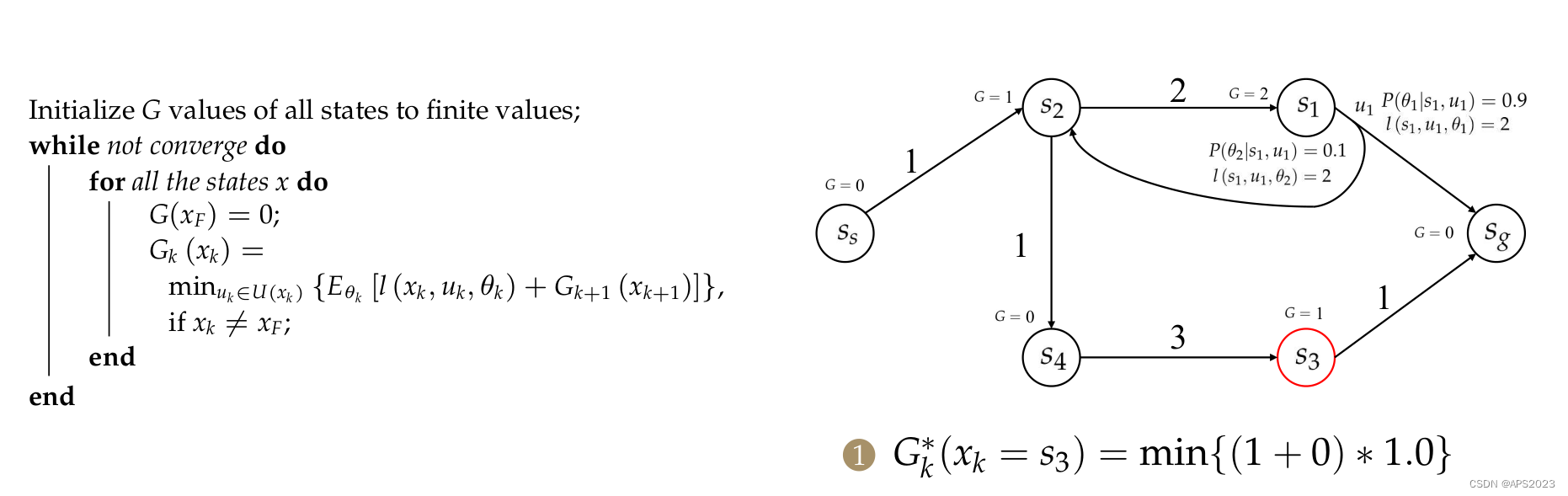
在来看
的更新:
在来看
的更新:
在来看
的更新:
最后对
的更新:
经过一轮之后我们有了G。我们接着进行第二轮迭代:
。。。。第三次迭代
如何判断收敛?边界条件??如何改进??迭代次序怎么来改进??
优点&缺点:
1.反映的是平均的水平
2.不一定是最优
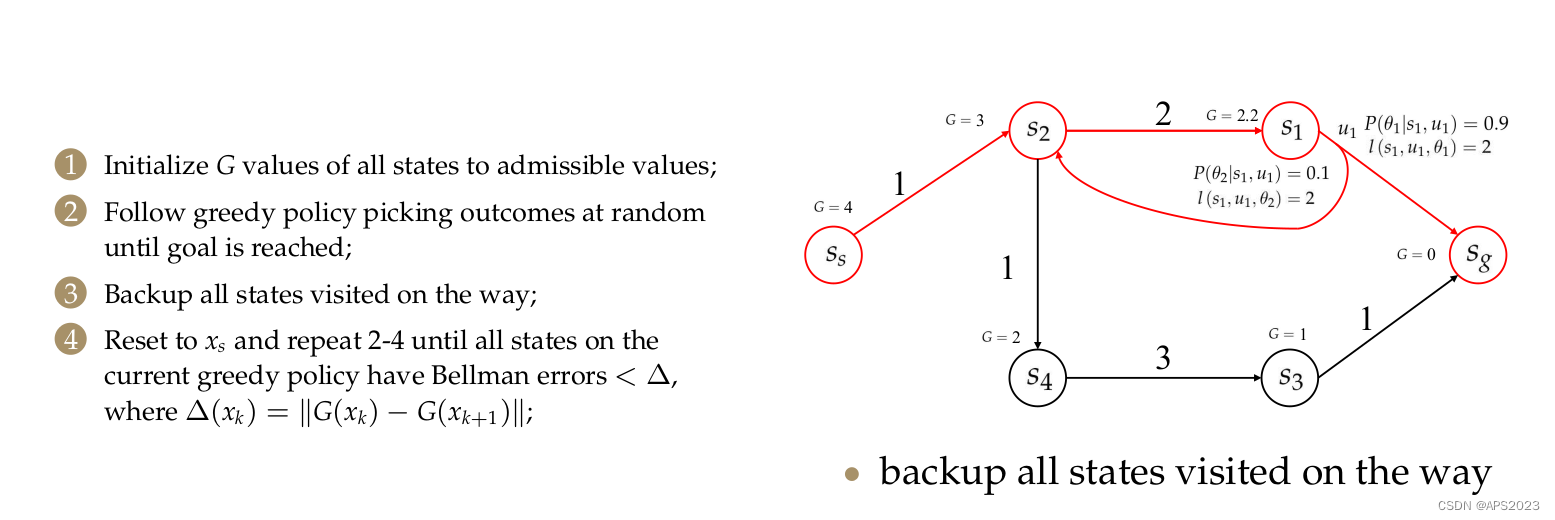
4 Real Time Dynamic Programming(RTDP)
看看实际例子吧:
根据每个节点到
的数量进行更新。
相关文章:

移动机器人路径规划(七)--- 基于MDP的路径规划MDP-Based Planning
目录 1 什么是MDP-Based Planning 2 worst-case analysis for nondeterministic model 3 Expected Cost Planning 4 Real Time Dynamic Programming(RTDP) 1 什么是MDP-Based Planning 之前我们从起点到终点存在很多可执行路径,我们可以…...

vue--The template root requires exactly one element.的解决办法
[vue/no-multiple-template-root] The template root requires exactly one element.eslint-plugin-vue 在vue中会出现以上问题 这是因为vue的模版中只有能一个根节点,所以在<template>中插入第二个元素就会报错 解决方案: 将<template>…...

嵌入式软件开发学习途径推荐
1、概述 嵌入式系统是当今智能化的重要组成部分,广泛应用于各行业和领域。学习内容多而杂,不同行业学习的内容也有一定差异。学习完一些基础课程后,工作中便是用到或根据就业方向去拓展自己的知识。这里推荐如下途径(后续可能会补充)…...
图书管理系统源码,图书管理系统开发,图书借阅系统源码三框架设计原理和说明
TuShuManger项目简介和创建 这里一共设计了6个项目,主要是借助三层架构思想分别设计了主要的三层,包括model实体层,Dal数据库操作层,Bll业务调用层,其他有公共使用项目common层,DButitly提取出来的数据库访问层,下面我们分别创建每个项目和开始搭建整个过程 TuShuManger…...

服务器被入侵了怎么去排查
在当今数字化时代,网络安全问题变得越来越重要。其中,服务器被入侵是一种常见的安全威胁。当服务器被入侵时,我们需要采取一系列措施来排查和解决问题。本文将为您提供服务器被入侵后的排查步骤。 第一步:确认服务器被入侵 当发现…...
、instanceOf和Array.isArray()的区别)
JavaScript中Object.prototype.toString.call()、instanceOf和Array.isArray()的区别
JavaScript是一种非常流行的编程语言,它具有许多强大的功能和特性。在JavaScript中,有一些方法和操作符可以帮助我们更好地处理数据类型和对象。本文将重点讨论Object.prototype.toString.call()、instanceOf和Array.isArray()这三个在JavaScript中常用的…...

Java串口通信入门教程
简介 串口通信是一种用于在计算机和外部设备之间进行数据交换的通信方式。在许多应用场景中,如物联网、自动化控制等领域,串口通信被广泛应用。本教程将带领您入门Java串口通信,介绍串口通信的基本原理和Java中的串口通信库,并提…...
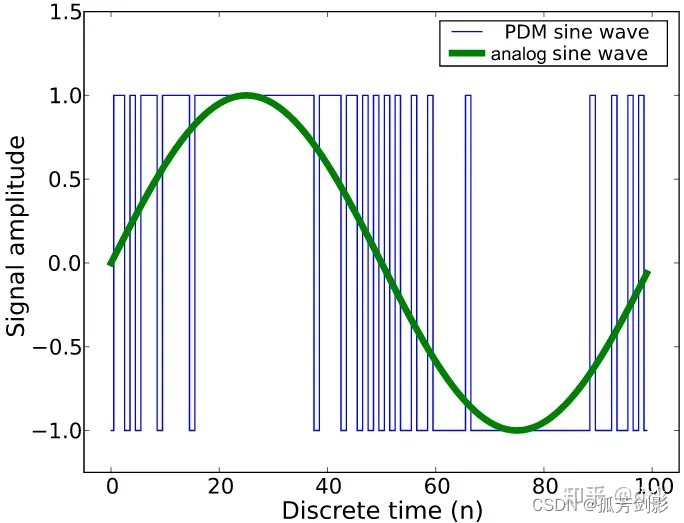
音频采集的相关基础知识
本文引注: https://zhuanlan.zhihu.com/p/652629744 1.麦克风的种类 (1)模拟麦克风 ECM麦克风:驻极体电容麦克风(ECM),典型的汽车ECM麦克风是一种将ECM单元与小型放大器电路整合在单个外壳中的装置。放大器提供一个模拟信号,其电压电平允许…...

vue中 多个请求,如果一个请出错,页面继续执行
vue中 多个请求,如果一个请出错,页面继续执行 在Vue中,可以通过Promise.all()方法来处理多个请求,即使其中一个请求出错,页面也可以继续执行其他的逻辑。 下面是一个示例代码,演示了如何在Vue中处理多个请…...
飞翔的小鸟小游戏
主类 package APP;import 框架.GameFrame;public class GameApp {public static void main(String[] args) {//游戏的入口new GameFrame();} }场景实物 package 框架;import 图导.Constant; import 图导.GameUtil;import java.awt.*; import java.awt.image.BufferedImage; …...

Visual Studio(VS) C++程序LNK2005错误,提示“error LNK2005: _XXX已经在xxx.obj中定义”解决方案
1.问题如图 2.出现原因 项目中有多个源文件或头文件,include后导致有些变量重复定义,加上Visual Studio新版版要求更严格 3.解决办法 查询到的解决办法很多不好用,此处记录解决自己问题的一个办法:直接让编译器忽略第二次定义的…...
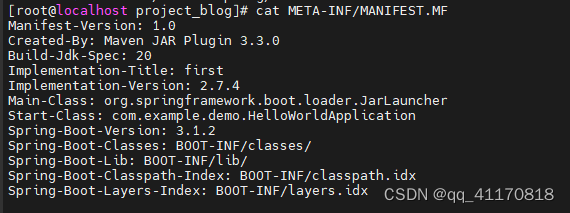
linux部署jar 常见问题
1.java -jar xxx.jar no main manifest attribute, in xxx.jar 一.no main manifest attribute, in xxx.jar 在pom.xml文件中加入: <plugin><groupId>org.springframework.boot</groupId><artifactId>spring-boot-maven-plugin</artifac…...

Arrays.asList() 与 Collections.singletonList()的恩怨情仇
1. 概述 列表是我们使用 Java 时常用的集合类型。 众所周知,我们可以轻松地用一行初始化一个List。例如,当我们想要初始化一个只有一个元素的List时,我们可以使用Arrays.asList()方法或Collections.singletonList()方法。 在本文中&#x…...
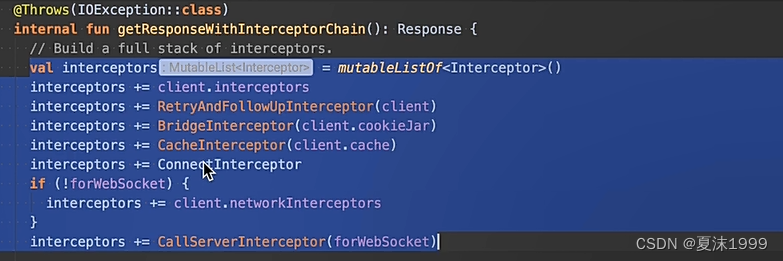
Okhttp 浅析
安全的连接 OkHttpClient: OkHttpClient: 1.线程调度 2.连接池,有则复用,没有就创建 3.interceptor 4.interceptor 5.监听工厂 6.是否失败重试 7.自动修正访问,如果没有权限或认证 8是否重定向 followRedirects 9.协议切换时候是否继续重定向 10.Cookie jar 容器 默认…...
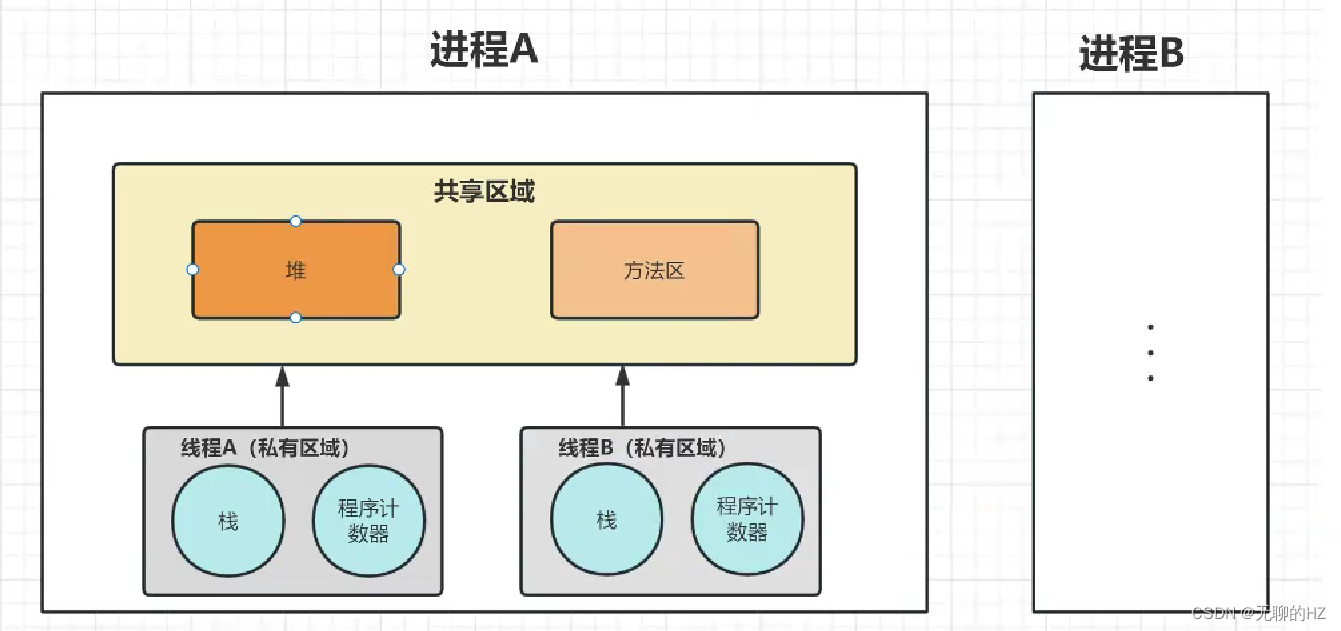
面试常见问题:什么是进程? 什么是线程?进程和线程有什么区别?
1.什么是进程? 进程是操作系统中一个程序在执行过程中的一个实例,每个进程都有自己独立的地址空间,进程间不共享内存。它是程序运行的最小内存单元; 进程特点: 1> 需要占用独立的内存空间; 2>可以并…...

什么是SQL?
SQL和MySQL是当今计算机领域中非常重要的两个概念。SQL是关系型数据库的查询语言,而MySQL是一种关系型数据库管理系统。它们在数据存储、管理和查询方面发挥着巨大的作用。在本文中,我们将深入探讨SQL和MySQL的定义、功能、应用以及它们之间的联系。 一…...
人力资源管理后台 === 基础环境+登陆
目录 1.人力资源项目介绍 1.1 项目架构和解决方案 1.2 课程安排 1.3 课程具备能力 1.4 课程地址 2. 拉取项目基础代码 3.项目目录和入口文件介绍 4.App.vue根组件解析 5.基础设置settings.js和导航守卫permission.js 6.Vuex的结构 7.使用模板中的Icon图标 8.扩展…...

Handler系列-怎么实现delay
1.前提 前面说到sendMessage携带的delay会被加上SystemClock.uptimeMillis() ,最终赋值给Message的when。 msg.when SystemClock.uptimeMillis() delayMillis; 那么when除了用来在链表里面作为排序依据以外,还在哪里用到了呢? 2.Looper…...

C++前缀和算法的应用:最大化城市的最小供电站数目
本文涉及的基础知识点 C算法:前缀和、前缀乘积、前缀异或的原理、源码及测试用例 包括课程视频 二分法 题目 给你一个下标从 0 开始长度为 n 的整数数组 stations ,其中 stations[i] 表示第 i 座城市的供电站数目。 每个供电站可以在一定 范围 内给所…...

Centos/Linux安装Apahce出现bug汇总
源码安装Apache软件 使用软件:Apahce2.4.58,apr1.5.2, apr-util1.5.4 1.下载apr、apr-util和Apache软件; 2.安装apr压缩包,步骤如下: 第一、解压缩 tar zxvf apr-1.5.2.tar.gz第二、安装 cd /usr/local/sr…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...