MATLAB在信号系统中的应用
1.产生一个幅度为1, 基频为2Hz,占空比为50%的周期方波.要求画出图形。
在MATLAB中,函数square(w0*t, DUTY)产生基本频率为w0 (周期T=2*pi/w0)、占空比DUTY= (τ/T)*100的周期矩形波(方波),默认情况下占空比DUTY=50。占空比指的是一个周期内,矩形波正电压持续的时间占整个周期的比例,即τ为一个周期中信号为正的时间长度,如果τ=T/2,那么DUTY=50,square(w0*t, 50)等同于square(w0*t)。
程序:
t=-4:0.0001:4;
A=2;T=pi;w0=2*pi/T;
ft=(1/2)*A*square(w0*t,50)+(1/2);
plot(t,ft);
axis([-4,4,-2,2]);运行结果:

2.产生一个Sa函数,理论上抽样信号Sa函数的定义为:
(要求画出图形)
MATLAB中有专门的命令sinc()产生抽样信号Sa函数.
程序:
t=-2*pi:0.01:2*pi;
y=sinc(t);
plot(t,y)
grid on运行结果:

3.已知系统的微分方程为:
求该系统的单位冲击响应并画图。注意:impulse调用格式
程序:
sys = tf([1, 3],[1, 3, 2]);
t = 0:0.1:10;
y = impulse(sys, t);
plot(t, y);运行结果:

4. 已知x1(n)= [1,1,1,0,1]-3,x2(n) = [2,2,2,2]-1
求:x(n) = x1(n) + x2(n) ,x(n) = x1(n) x2(n),并画图。
程序:
x1=[1,1,1,0,1];
ns1=-3;
x2=[2,2,2,2];
ns2=-1;
nf1=ns1+length(x1)-1;
nf2=ns2+length(x2)-1;
ny=min(ns1,ns2):max(nf1,nf2);
xa1=zeros(1,length(ny));xa2=xa1;
xa1(find((ny>=ns1)&(ny<=nf1)==1))=x1;
xa2(find((ny>=ns2)&(ny<=nf2)==1))=x2;
ya=xa1+xa2
yp=xa1.*xa2
subplot(4,1,1),stem(ny,xa1,'.')
subplot(4,1,2),stem(ny,xa2,'.')
line([ny(1),ny(end)],[0,0])
subplot(4,1,3),stem(ny,ya,'.')
line([ny(1),ny(end)],[0,0])
subplot(4,1,4),stem(ny,yp,'.')
line([ny(1),ny(end)],[0,0])运行结果:
ya =
1 1 3 2 3 2
yp =
0 0 2 0 2 0


5.利用函数impz和stepz求离散系统

的单位序列响应h(k)和单位阶跃响应g(k)。
程序:
a=[1 0 1/3 0];
b=[1/6 1/2 1/2 1/6];
N=32;
n=0:N-1;hn=impz(b,a,n);
gn=dstep(b,a,n+1);
subplot(1,2,1),stem(n,hn);
title('系统单位冲激函数')
axis([0 N 1.1*min(hn) 1.1*max(hn)])subplot(1,2,2),stem(n,gn);
title('系统单位阶跃函数')
axis([0 N 1.1*min(gn) 1.1*max(gn)])运行结果:

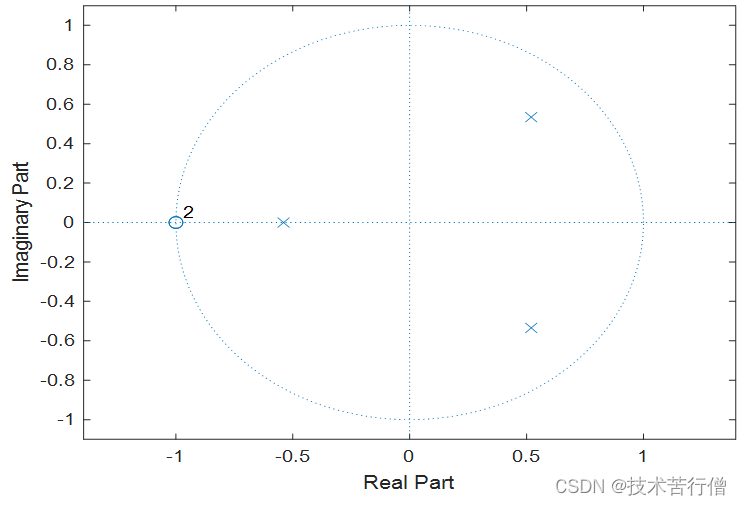
6.已知一离散因果系统的系统函数为:
利用MATLAB求出系统函数的零点和极点,并在Z平面显示它们的分布。
在MATLAB中可以借助函数tf2zp来直接得到系统函数的零点和极点的值,并通过函数zplane来显示其零点和极点的分布。
程序:
b=[1 2 1];
a=[1 -0.5 -0.005 0.3];
[z,p,k]=tf2zp(b,a);
B=[0 1 2 1];
A=[1 -0.5 -0.005 0.3];
figure
zplane(B,A);运行结果:
相关文章:

MATLAB在信号系统中的应用
1.产生一个幅度为1, 基频为2Hz,占空比为50%的周期方波.要求画出图形。 在MATLAB中,函数square(w0*t, DUTY)产生基本频率为w0 (周期T2*pi/w0)、占空比DUTY (τ/T)*100的周期矩形波(方波),默认情况下占空比DUTY50。占空…...
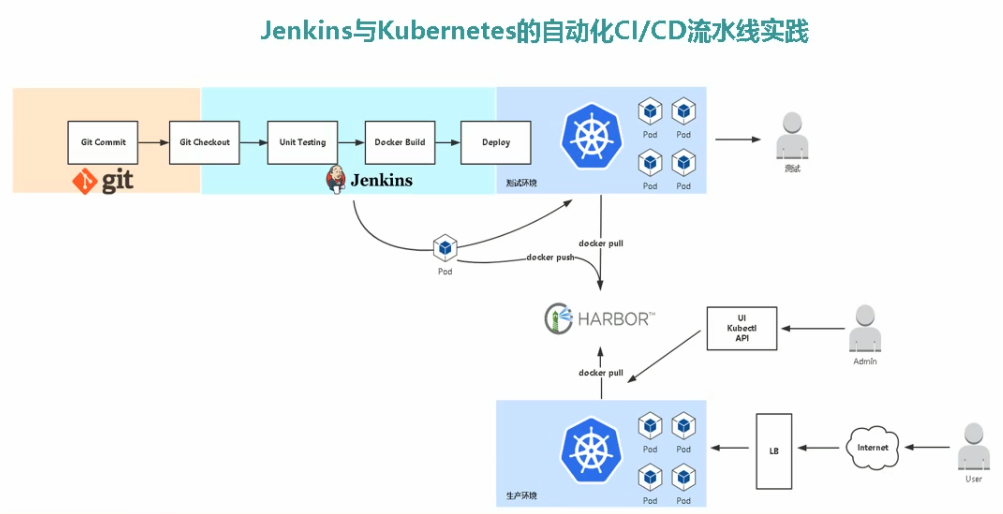
Jenkins与Docker的自动化CI/CD流水线实践
Pipeline 有诸多优点,例如: 项目发布可视化,明确阶段,方便处理问题 一个Jenkins File文件管理整个项目生命周期 Jenkins File可以放到项目代码中版本管理 Jenkins管理界面 操作实例:Pipeline的简单使用 这里是比较…...

企业数字化转型的作用是什么?_光点科技
在当今快速变化的商业环境中,数字化转型已成为企业发展的重要策略。企业数字化转型指的是利用数字技术改造传统业务模式和管理方式,以提升效率、增强竞争力和创造新的增长机会。 提升运营效率:数字化转型通过引入自动化工具和智能系统&#x…...

css加载会造成阻塞吗??
前言 前几天面试问到了这个问题,当时这个答得不敢确定哈哈,虽然一面还是过了 现在再分析下这个,总结下,等下次遇到就能自信得回答,666 准备工作 为了完成本次测试,先来科普一下,如何利用chr…...
——第16期)
Java中的jvm——面试题+答案(JVM的高级概念和调优技巧,包括垃圾回收、内存分析、优化技术等)——第16期
涉及Java虚拟机(JVM)高级概念和调优技巧的面试题以及简要答案: 什么是JVM调优?有哪些常见的JVM调优参数? 答案: JVM调优是通过调整JVM的参数和配置,以提高Java应用程序的性能和稳定性。常见的JV…...

***Linux下Mysql的安装
以下是在Linux系统下安装MySQL的步骤: 1.访问MySQL官网下载页面(https://dev.mysql.com/downloads/mysql/),选择适合您Linux系统的版本进行下载。 2.下载完成后,解压缩文件并将其移动到/usr/local目录下:…...

Linux踩坑:arm下gcc编译添加 -Ox 优化后,程序无法正常运行
arm下gcc编译添加 -Ox 优化后,程序无法正常运行 一、问题描述 今天学习正点原子的阿尔法开发板裸机开发的时候,遇到了一个问题,在没有使用 -Ox 优化的时候,编译出来的程序能够正常运行,但是添加了-Ox之后,…...

Vue3中Composition API介绍
在Vue 3中,引入了Composition API,它是一种新的组合式函数API,用于更灵活地组织和重用组件逻辑。Composition API相比于Vue 2中的Options API,提供了更好的可组合性和代码复用性。下面是对Vue 3中Composition API的介绍和用法&…...
Centos7下搭建Android开发环境及Android真机调试)
虚拟机系列:(VMware Workstation Pro)Centos7下搭建Android开发环境及Android真机调试
一、Android SDK 安装配置 1、环境 Linux系统为:Red Hat Enterprise Linux 7 64 位 ; 当然还需要Java环境,java 环境这里不叙述; 2、Android Studio 安装 (1)下载位置: http://www.android-studio.org/ 我这里下载的:android-studio-ide-191.5977832-linux.tar.gz …...
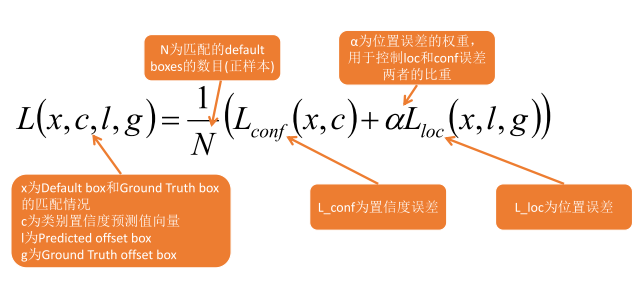
全面(16万字)深入探索深度学习:基础原理到经典模型网络的全面解析
前言 Stacking(堆叠) 网页调试 学习率:它决定了模型在每一次迭代中更新参数的幅度激活函数-更加详细 激活函数的意义: 激活函数主要是让模型具有非线性数据拟合的能力,也就是能够对非线性数据进行分割/建模 如果没有激活函数: 第一个隐层: l…...
openEuler Linux 部署 FineBi
openEuler Linux 部署 FineBi 部署环境 环境版本openEuler Linux22.03MySQL8.0.35JDK1.8FineBi6.0 环境准备 升级系统内核和软件 yum -y updatereboot安装常用工具软件 yum -y install vim tar net-tools 安装MySQL8 将 MySQL Yum 存储库添加到系统的存储库列表中 sudo…...

QThreadStorage使用介绍
作者:令狐掌门 技术交流QQ群:675120140 csdn博客:https://mingshiqiang.blog.csdn.net/ 文章目录 什么是线程数据存储Qt中的线程数据存储`QThreadStorage` 的用法:代码示例什么是线程数据存储 线程数据存储是指为每个线程在程序中分配和管理数据的过程。它主要用于并发编程…...

AI和人工智能与机器学习全景报告
今天分享的是AI系列深度研究报告:《AI和人工智能与机器学习全景报告》。 (报告出品方:appen) 报告共计:30页 获取 数据获取仍是AI应用构建团队的主要瓶颈。 原因各不相同。例如,特定用例的数据可能不足…...

【计算机网络】(网络层)定长掩码和变长掩码
目录 1、IPV4地址的应用规划 2、例题分析 2.1、定长的子网掩码 2.2、变长的子网掩码 1、IPV4地址的应用规划 定长的子网掩码(FLSM): 使用同一个子网掩码划分子网,每个子网所分配的IP地址数量相同,造成IP地址的浪费…...
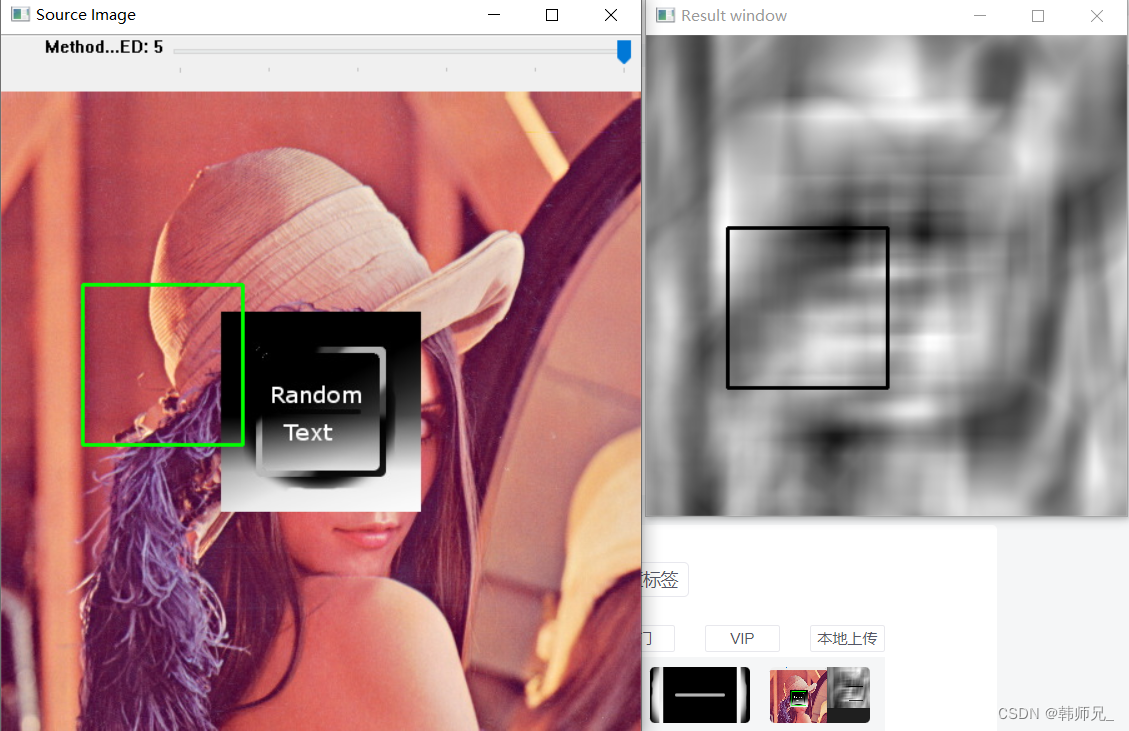
008 OpenCV matchTemplate 模板匹配
目录 一、环境 二、模板匹配算法原理 三、代码演示 一、环境 本文使用环境为: Windows10Python 3.9.17opencv-python 4.8.0.74 二、模板匹配算法原理 cv.matchTemplate是OpenCV库中的一个函数,用于在图像中查找与模板匹配的特征。它的主要应用场景…...

PTA 海盗分赃
P 个海盗偷了 D 颗钻石后来到公海分赃,一致同意如下分赃策略: 首先,P 个海盗通过抽签决定 1 - P 的序号。然后由第 1 号海盗提出一个分配方案(方案应给出每个海盗分得的具体数量),如果能够得到包括 1 号在…...
零基础学Linux内核:1、Linux源码组织架构
文章目录 前言一、Linux内核的特征二、Linux操作系统结构1.Linux在系统中的位置2.Linux内核的主要子系统3、Linux系统主要数据结构 三、linux内核源码组织1、下载Linux源码2、Linux版本号3、linux源码架构目录讲解 前言 这里将是我们从零开始学习Linux的第一节,这节…...

STM32中Msp函数的意义
msp(MCU Support Package) 举个例子:串口初始化函数HAL_UART_Init()与串口底层初始化函数HAL_UART_MspInit() HAL_UART_Init()用于初始化串口通讯协议如波特率、有效位等 HAL_UART_MspInit()用于初始化于MCU相关的配置比如时钟、NVIC、GPI…...
PTA NeuDs_数据库题目
二.单选题 1.数据库应用程序的编写是基于数据库三级模式中的。 A.模式 B.外模式 C.内模式 D.逻辑模式 用户应用程序根据外模式进行数据操作,通过外模式一模式映射,定义和建立某个外模式与模式间的对应关系 2.对创建数据库模式一类的数据库对象的授权…...
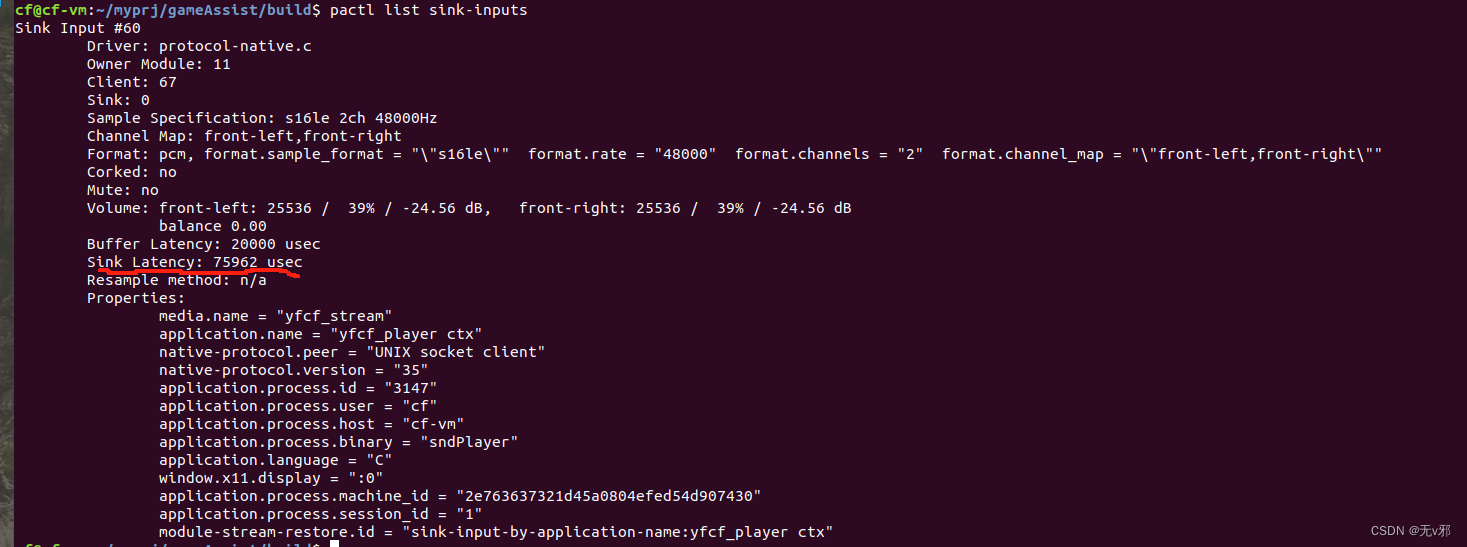
pulseaudio是如何测试出音频延迟的
通常专业的音频设备生产厂商都有专业的设备来测试精确的音频链路延时。 那么没有专业设备怎么测试出音频延迟呢?如下图,我们可以看到pulseaudio可以测试出硬件音频延迟。 那么,他是怎么测试出硬件延迟的呢?他的理论依据是什么呢?接下来我带大伙一起探索一下。 /*占位…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

基于开源AI智能名片链动2 + 1模式S2B2C商城小程序的沉浸式体验营销研究
摘要:在消费市场竞争日益激烈的当下,传统体验营销方式存在诸多局限。本文聚焦开源AI智能名片链动2 1模式S2B2C商城小程序,探讨其在沉浸式体验营销中的应用。通过对比传统品鉴、工厂参观等初级体验方式,分析沉浸式体验的优势与价值…...

Linux中INADDR_ANY详解
在Linux网络编程中,INADDR_ANY 是一个特殊的IPv4地址常量(定义在 <netinet/in.h> 头文件中),用于表示绑定到所有可用网络接口的地址。它是服务器程序中的常见用法,允许套接字监听所有本地IP地址上的连接请求。 关…...



