【数据结构】树与二叉树(廿六):树删除指定结点及其子树(算法DS)
文章目录
- 5.3.1 树的存储结构
- 5. 左儿子右兄弟链接结构
- 5.3.2 获取结点的算法
- 1. 获取大儿子、大兄弟结点
- 2. 搜索给定结点的父亲
- 3. 搜索指定数据域的结点
- 4. 删除结点及其左右子树
- a. 逻辑删除与物理删除
- b. 算法DST
- c. 算法解析
- d. 代码实现
- 递归释放树
- 算法DS
- e. 算法测试
- 5. 代码整合
5.3.1 树的存储结构
5. 左儿子右兄弟链接结构
【数据结构】树与二叉树(十九):树的存储结构——左儿子右兄弟链接结构(树、森林与二叉树的转化)
左儿子右兄弟链接结构通过使用每个节点的三个域(FirstChild、Data、NextBrother)来构建一棵树,同时使得树具有二叉树的性质。具体来说,每个节点包含以下信息:
- FirstChild: 存放指向该节点的大儿子(最左边的子节点)的指针。这个指针使得我们可以迅速找到一个节点的第一个子节点。
- Data: 存放节点的数据。
- NextBrother: 存放指向该节点的大兄弟(同一层中右边的兄弟节点)的指针。这个指针使得我们可以在同一层中迅速找到节点的下一个兄弟节点。
通过这样的结构,整棵树可以用左儿子右兄弟链接结构表示成一棵二叉树。这种表示方式有时候被用于一些特殊的树结构,例如二叉树、二叉树的森林等。这种结构的优点之一是它更紧凑地表示树,而不需要额外的指针来表示兄弟关系。
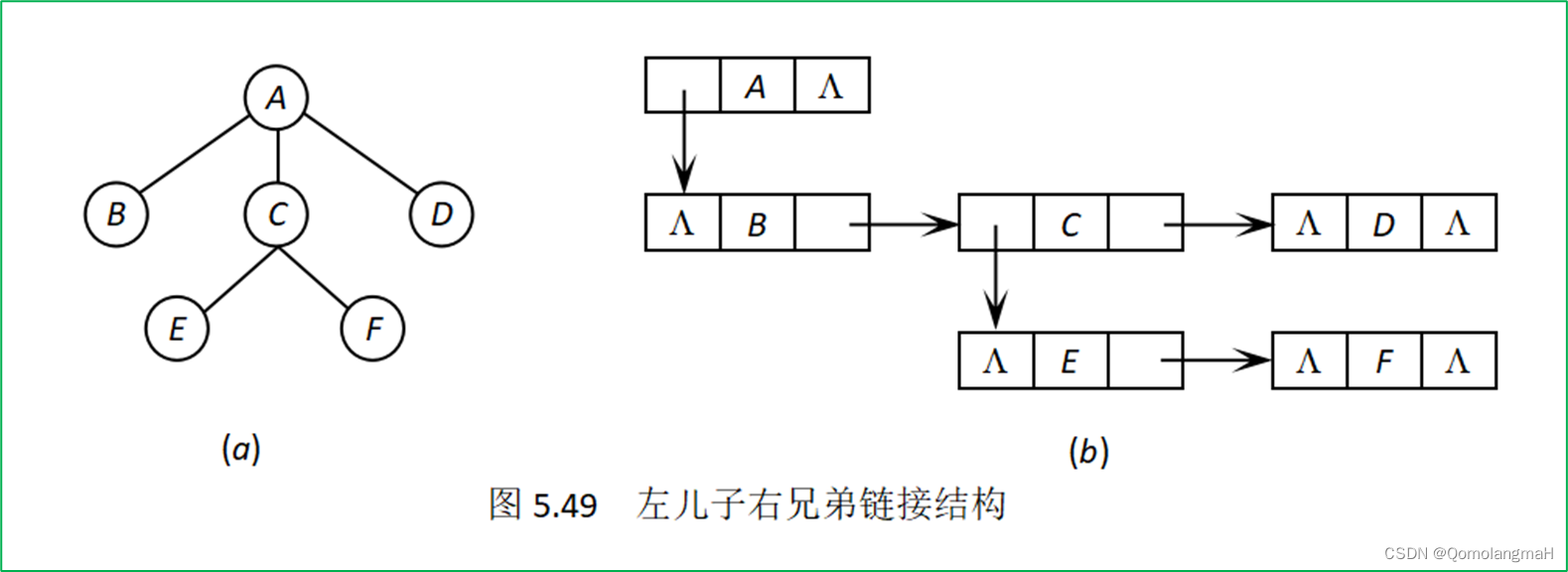
A/|\B C D/ \E F
A
|
B -- C -- D|E -- F
即:
A/ B \C/ \ E D\F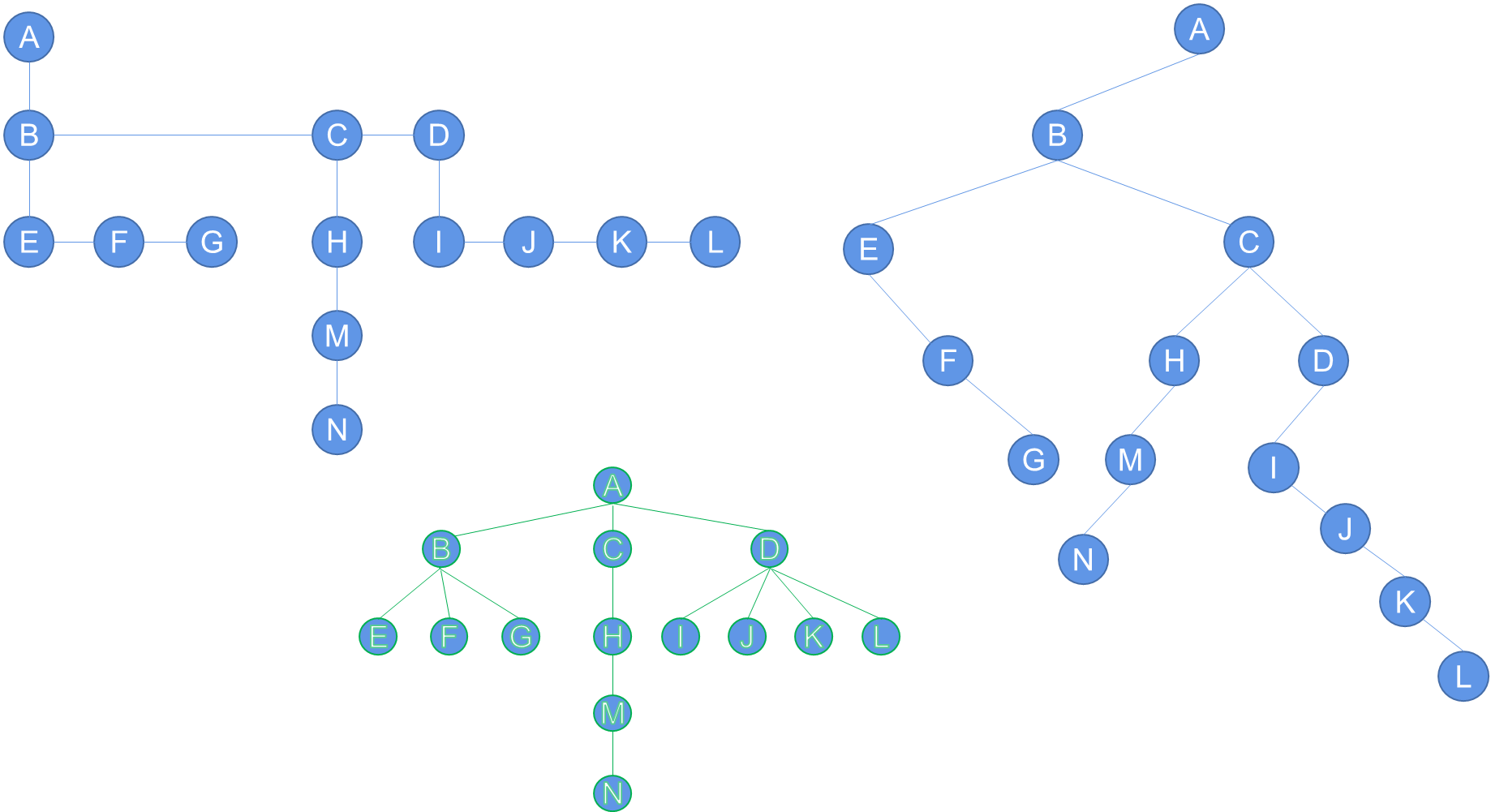
5.3.2 获取结点的算法
1. 获取大儿子、大兄弟结点
【数据结构】树与二叉树(二十):树获取大儿子、大兄弟结点的算法(GFC、GNB)
2. 搜索给定结点的父亲
【数据结构】树与二叉树(廿四):树搜索给定结点的父亲(算法FindFather)
3. 搜索指定数据域的结点
【数据结构】树与二叉树(廿五):树搜索指定数据域的结点(算法FindTarget)
4. 删除结点及其左右子树
a. 逻辑删除与物理删除
- 逻辑删除(Logical Deletion)
- 逻辑删除通常是指在数据结构中标记某个节点为被删除的状态,而不是真正地从内存中删除它。
- 物理删除(Physical Deletion)
- 物理删除是指真正地从内存中释放某个节点及其子树的内存。
b. 算法DST

c. 算法解析
-
检查输入参数t和p是否为空,如果其中任一参数为空,则返回。
-
调用
FindFather(t, p.result)函数,找到以t为根的树中根为p的子树的父节点 -
如果找不到父节点(即result为空),则表示根为p的子树不存在,直接删除节点p并返回。
-
如果找到了父节点,算法继续执行,检查父节点的第一个子节点是否为p
- 如果第一个子节点是p,则将父节点的第一个子节点设置为p的下一个兄弟节点(即FirstChild(result)←NextBrother( p)),然后删除节点p并返回。
- 如果第一个子节点不是p,则算法使用一个循环找到p的下一个兄弟节点q,将q的下一个兄弟节点设置为p的下一个兄弟节点(即NextBrother(q)←NextBrother( p))。最后,删除节点p并返回。
d. 代码实现
递归释放树
void freeTree(TreeNode* root) {if (root != NULL) {freeTree(root->firstChild);freeTree(root->nextBrother);free(root);}
}
算法DS
void DelSubtree(TreeNode* t, TreeNode* p) {if (t == NULL || p == NULL) {return;}TreeNode* result = NULL;FindFather(t, p, &result);if (result == NULL) {return; // 未找到父亲节点}if (result->firstChild == p) {result->firstChild = p->nextBrother;freeTree(p);return;}TreeNode* q = result->firstChild;while (q != NULL && q->nextBrother != p) {q = q->nextBrother;}if (q != NULL) {q->nextBrother = p->nextBrother;freeTree(p);}
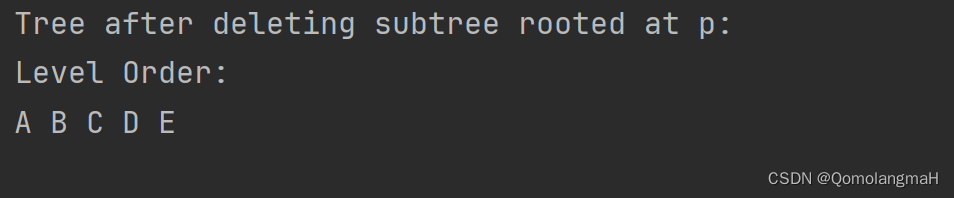
}e. 算法测试
int main() {// 构建左儿子右兄弟链接结构的树TreeNode* A = createNode('A');TreeNode* B = createNode('B');TreeNode* C = createNode('C');TreeNode* D = createNode('D');TreeNode* E = createNode('E');TreeNode* F = createNode('F');A->firstChild = B;B->nextBrother = C;C->nextBrother = D;C->firstChild = E;E->nextBrother = F;// 要删除的子树的根节点TreeNode* subtreeRoot = F;// 使用算法 DelSubtree 删除子树DelSubtree(A, subtreeRoot);// 输出删除子树后的树结构printf("Tree after deleting subtree rooted at %c:\n", subtreeRoot->data);// 层次遍历算法printf("Level Order: \n");LevelOrder(A);printf("\n");// 释放树节点freeTree(A);return 0;
}- 继续采用先前系列文章的树结构
- 删除指定结点subtreeRoot
- 层次遍历删除subtreeRoot结点及其子树后的树
- 释放整棵树
5. 代码整合
#include <stdio.h>
#include <stdlib.h>// 定义树节点
typedef struct TreeNode {char data;struct TreeNode* firstChild;struct TreeNode* nextBrother;
} TreeNode;// 创建树节点
TreeNode* createNode(char data) {TreeNode* newNode = (TreeNode*)malloc(sizeof(TreeNode));if (newNode != NULL) {newNode->data = data;newNode->firstChild = NULL;newNode->nextBrother = NULL;}return newNode;
}// 释放树节点及其子树
void freeTree(TreeNode* root) {if (root != NULL) {freeTree(root->firstChild);freeTree(root->nextBrother);free(root);}
}// 算法GFC:获取大儿子结点
TreeNode* getFirstChild(TreeNode* p) {if (p != NULL && p->firstChild != NULL) {return p->firstChild;}return NULL;
}// 算法GNB:获取下一个兄弟结点
TreeNode* getNextBrother(TreeNode* p) {if (p != NULL && p->nextBrother != NULL) {return p->nextBrother;}return NULL;
}// 队列结构
typedef struct QueueNode {TreeNode* treeNode;struct QueueNode* next;
} QueueNode;typedef struct {QueueNode* front;QueueNode* rear;
} Queue;// 初始化队列
void initQueue(Queue* q) {q->front = NULL;q->rear = NULL;
}// 入队列
void enqueue(Queue* q, TreeNode* treeNode) {QueueNode* newNode = (QueueNode*)malloc(sizeof(QueueNode));newNode->treeNode = treeNode;newNode->next = NULL;if (q->rear == NULL) {q->front = newNode;q->rear = newNode;} else {q->rear->next = newNode;q->rear = newNode;}
}// 出队列
TreeNode* dequeue(Queue* q) {if (q->front == NULL) {return NULL; // 队列为空}TreeNode* treeNode = q->front->treeNode;QueueNode* temp = q->front;q->front = q->front->next;free(temp);if (q->front == NULL) {q->rear = NULL; // 队列为空}return treeNode;
}// 层次遍历的算法
void LevelOrder(TreeNode* root) {if (root == NULL) {return;}Queue queue;initQueue(&queue);enqueue(&queue, root);while (queue.front != NULL) {TreeNode* p = dequeue(&queue);while (p != NULL) {// 访问当前结点printf("%c ", p->data);// 将大儿子结点入队列if (getFirstChild(p) != NULL) {enqueue(&queue, getFirstChild(p));}// 移动到下一个兄弟结点p = getNextBrother(p);}}
}// 算法 FindFather
void FindFather(TreeNode* t, TreeNode* p, TreeNode** result) {*result = NULL;if (t == NULL || p == NULL || p == t) {return;}TreeNode* q = t->firstChild;while (q != NULL) {if (q == p) {*result = t;return;}FindFather(q, p, result);if (*result != NULL) {return;}q = q->nextBrother;}
}// 算法 DelSubtree
void DelSubtree(TreeNode* t, TreeNode* p) {if (t == NULL || p == NULL) {return;}TreeNode* result = NULL;FindFather(t, p, &result);if (result == NULL) {return; // 未找到父亲节点}if (result->firstChild == p) {result->firstChild = p->nextBrother;freeTree(p);return;}TreeNode* q = result->firstChild;while (q != NULL && q->nextBrother != p) {q = q->nextBrother;}if (q != NULL) {q->nextBrother = p->nextBrother;freeTree(p);}
}int main() {// 构建左儿子右兄弟链接结构的树TreeNode* A = createNode('A');TreeNode* B = createNode('B');TreeNode* C = createNode('C');TreeNode* D = createNode('D');TreeNode* E = createNode('E');TreeNode* F = createNode('F');A->firstChild = B;B->nextBrother = C;C->nextBrother = D;C->firstChild = E;E->nextBrother = F;// 要删除的子树的根节点TreeNode* subtreeRoot = F;// 使用算法 DelSubtree 删除子树DelSubtree(A, subtreeRoot);// 输出删除子树后的树结构printf("Tree after deleting subtree rooted at %c:\n", subtreeRoot->data);// 层次遍历算法printf("Level Order: \n");LevelOrder(A);printf("\n");// 释放树节点freeTree(A);return 0;
}相关文章:

【数据结构】树与二叉树(廿六):树删除指定结点及其子树(算法DS)
文章目录 5.3.1 树的存储结构5. 左儿子右兄弟链接结构 5.3.2 获取结点的算法1. 获取大儿子、大兄弟结点2. 搜索给定结点的父亲3. 搜索指定数据域的结点4. 删除结点及其左右子树a. 逻辑删除与物理删除b. 算法DSTc. 算法解析d. 代码实现递归释放树算法DS e. 算法测试 5. 代码整合…...

交叉编译 和 软硬链接 的初识(面试重点)
目录 交叉编译的初认识Q&A Q1: 编译是什么? Q2: 交叉编译是什么? Q3: 为什么要交叉编译 Q3.1:树莓派相对于C51大得多,可以集成编译器比如gcc,那么树莓派就不需要交叉编译了吗? Q4: 什么是宿主机和…...

Docker attach 命令
docker attach:连接到正在运行中的容器。 语法 docker attach [OPTIONS] CONTAINER要attach上去的容器必须正在运行,可以同时连接上同一个container来共享屏幕(与screen命令的attach类似)。 官方文档中说attach后可以通过CTRL-…...
Keil5个性化设置及常用快捷键
Keil5个性化设置及常用快捷键 1.概述 这篇文章是Keil工具介绍的第三篇文章,主要介绍下Keil5优化配置,以及工作中常用的快捷键提高开发效率。 第一篇:《安装嵌入式单片机开发环境Keil5MDK以及整合C51开发环境》https://blog.csdn.net/m0_380…...
rtsp点播异常出现‘circluar_buffer_size‘ option was set but it is xx
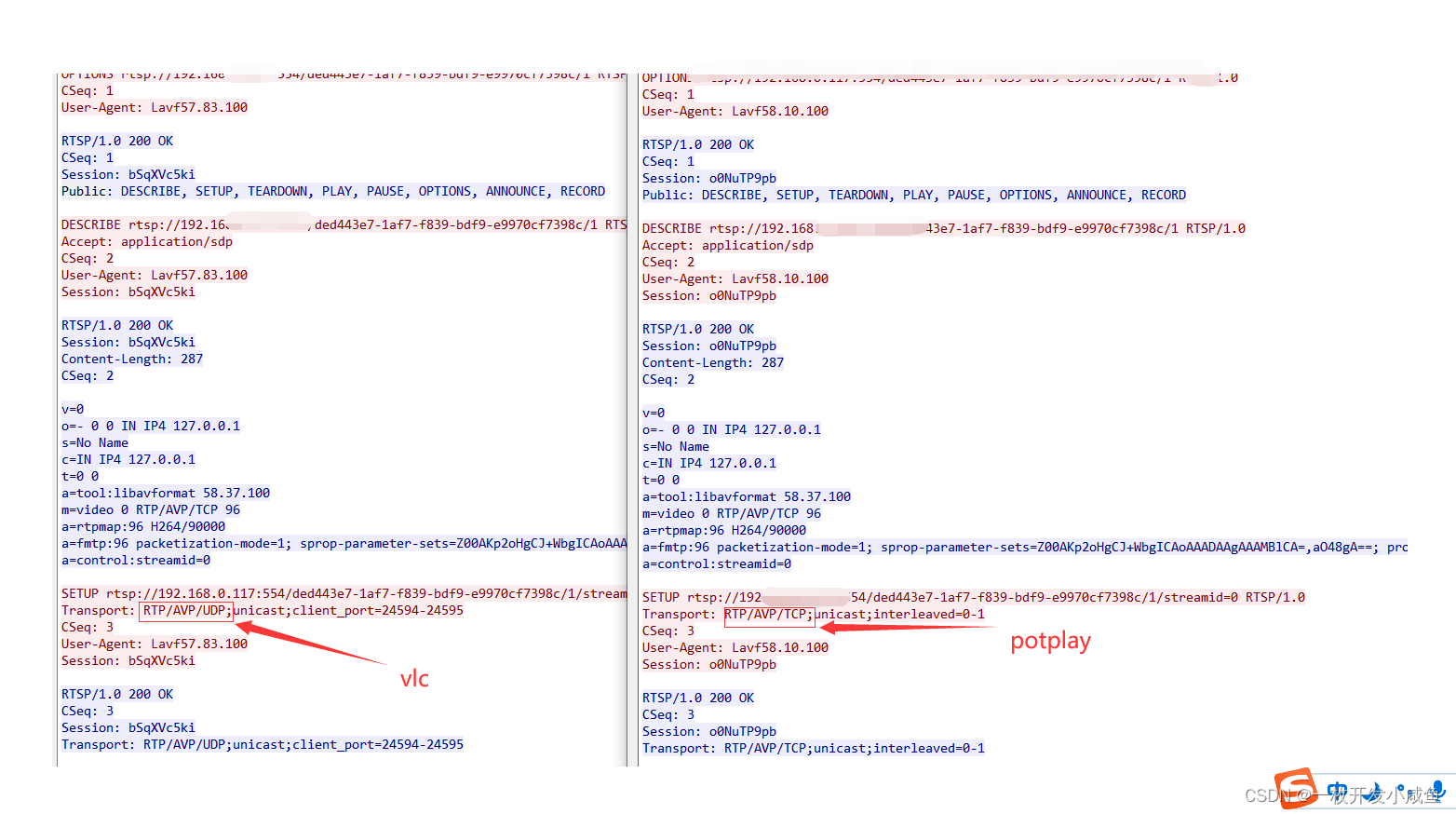
先说现象: 我使用potplay播放器来点播rtsp码流的时候可以点播成功,同事使用vlc和FFplay来点播rtsp码流的时候异常。 排查思路: 1.开始怀疑是oss账号问题,因为ts切片数据是保存在oss中的,我使用的是自己的oss账号,同事使用的是公司…...

C++ Qt QString用法详解与代码演示
作者:令狐掌门 技术交流QQ群:675120140 csdn博客:https://mingshiqiang.blog.csdn.net/ 文章目录 创建和初始化长度和容量修改字符串字符串比较查找和提取数值转换arg格式化`arg` 的基本用法精确控制占位符多占位符的复杂替换使用大括号占位符注意事项迭代Unicode 和编码QSt…...

安全攻击及防范手册
目录 1 概述 1.1 简介 1.2 参考资料 2 安全隐患及预防措施 <...
Visual Studio 使用MFC 单文档工程绘制单一颜色直线和绘制渐变颜色的直线(实例分析)
Visual Studio 使用MFC 单文档工程从创建到实现绘制单一颜色直线和绘制渐变颜色的直线 本文主要从零开始创建一个MFC单文档工程然后逐步实现添加按键(事件响应函数),最后实现单一颜色直线的绘制与渐变色直线的绘制o( ̄▽࿾…...

一起学docker系列之八使用 Docker 安装配置 MySQL
目录 前言步骤 1:拉取 MySQL 镜像步骤 2:运行 MySQL 容器步骤 3:检查容器状态步骤 4:进入 MySQL 容器步骤 5:配置 MySQL 字符编码步骤 6:重启 MySQL 容器步骤 7:测试字符编码步骤 8:…...
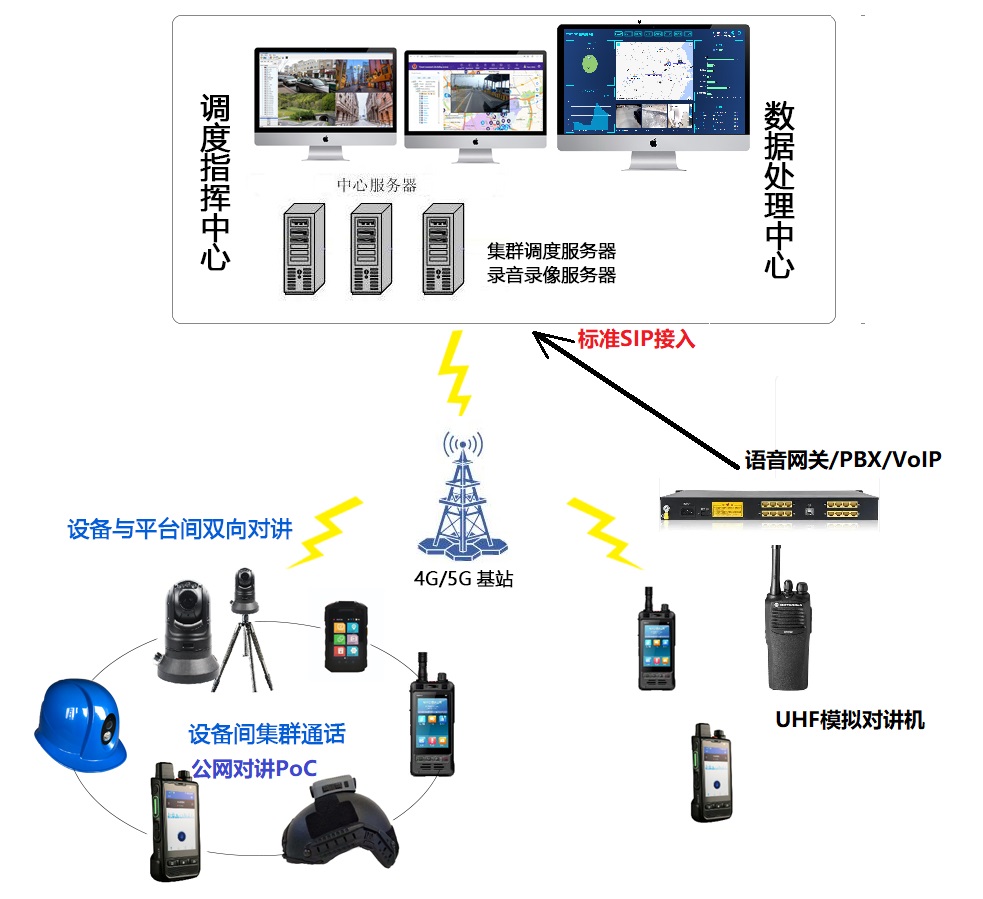
4G执法记录仪在大型安保集团,保安集团、蓝天救援队中的 应用,行为规范化,人员定位,考勤打卡,应急指挥调度
【智能化升级】揭秘4G/5G执法记录仪在安保与救援领域如何重塑行业标准与效率 在快速发展的社会当中,大型安保集团、保安集团和蓝天救援队所肩负的任务日益繁重与复杂。无论是在平时的治安巡查、安保执勤,还是在突发公共事件的应急响应中,如何…...

分布式事务,一致性理论, 两阶段提交(2PC), 三阶段提交(3PC),Seata分布式事务方案
文章目录 分布式事务:1、一致性理论2、两阶段提交(2PC)3、三阶段提交(3PC)4、Seata分布式事务方案 上一篇降到了 分布式锁,先来和大家聊一聊分布式事务, 分布式锁的链接如下: http…...
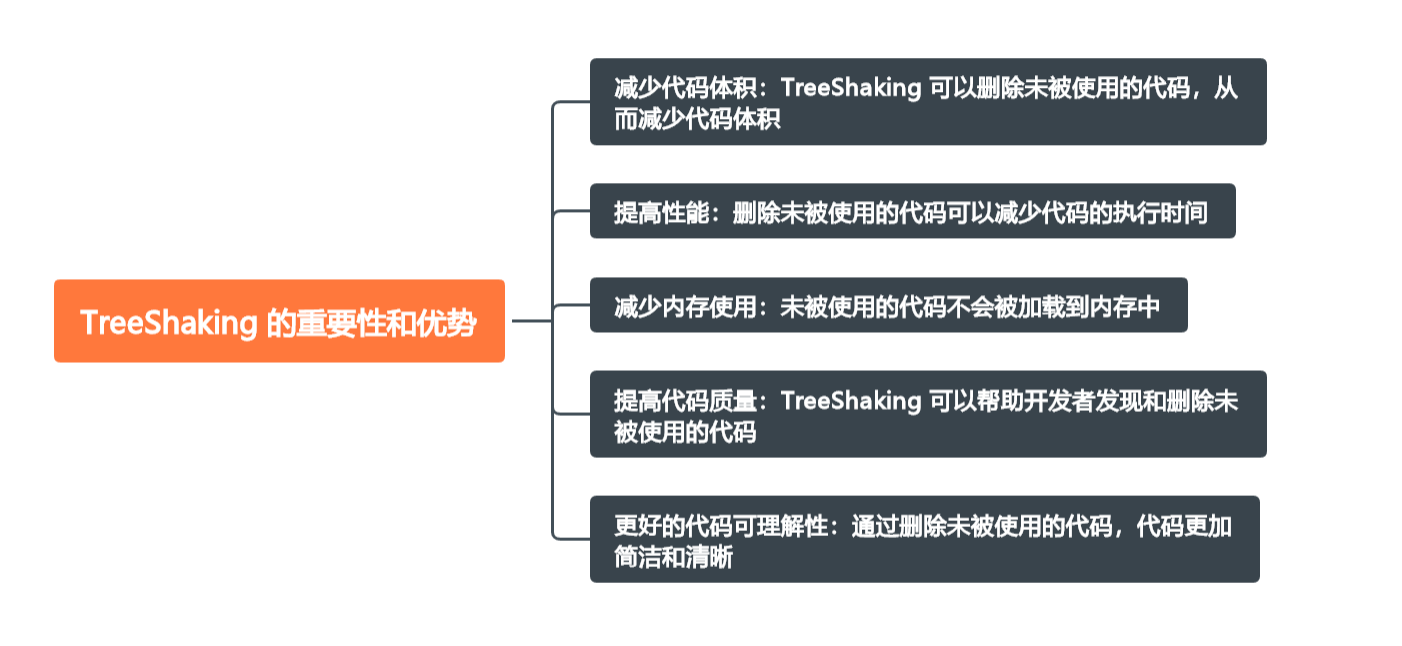
摆脱无用代码的负担:TreeShaking 的魔力
🤍 前端开发工程师(主业)、技术博主(副业)、已过CET6 🍨 阿珊和她的猫_CSDN个人主页 🕠 牛客高级专题作者、在牛客打造高质量专栏《前端面试必备》 🍚 蓝桥云课签约作者、已在蓝桥云…...
)
A-莲子的软件工程学【算法必会题目】(JavaPythonC++实现)
文章目录 A-莲子的软件工程学题目背景解题思路Python题解代码Java题解代码C++题解代码代码OJ评判结果代码讲解Python 代码解释:Java 代码解释:C++ 代码解释:寄语A-莲子的软件工程学 题目背景 在宇宙射线的轰击下,莲子电脑里的一些她自己预定义的函数被损坏了。 对于一名…...
STM32-SPI1控制AD7705(Sigma-Delta-ADC芯片)
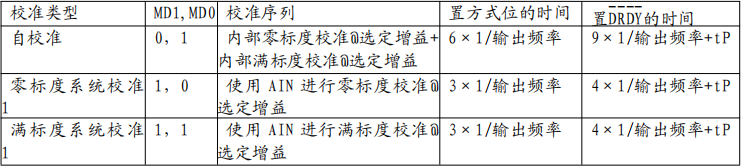
STM32-SPI1控制AD7705(Sigma-Delta-ADC芯片) 原理图手册说明功能方框图引脚功能 片内寄存器通信寄存器(RS2、RS1、RS00、0、0)设置寄存器时钟寄存器数据寄存器(RS2、RS1、RS00、1、1)测试寄存器(…...

13年老鸟总结,性能测试方法汇总+性能响应很慢排查方法(详全)
目录:导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜) 前言 1、性能测试包含哪…...

[网络] 3. HTTP 3 与 HTTP 2 有什么区别
协议不同 HTTP2 是基于 TCP 协议实现的 HTTP3 是基于 UDP 协议实现的QUIC HTTP3 新增了 QUIC 协议来实现可靠性的传输握手次数 HTTP2 是基于 HTTPS 实现的,建立连接需要先进行 TCP 3次握手,然后再进行 TLS 3次握手,总共6次握手。 HTTP3 只需要…...
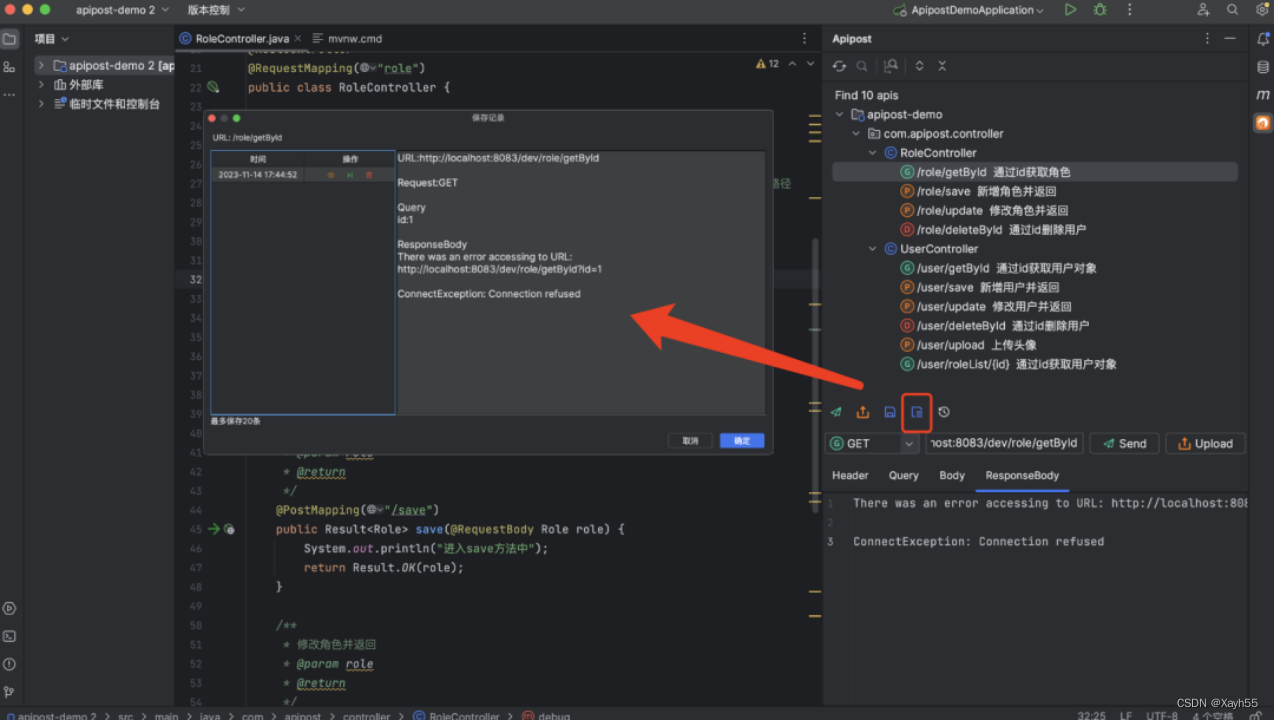
IDEA中的Postman?完全免费!
Postman是大家最常用的API调试工具,那么有没有一种方法可以不用手动写入接口到Postman,即可进行接口调试操作?今天给大家推荐一款IDEA插件:Apipost Helper,写完代码就可以调试接口并一键生成接口文档!而且还…...

用JAVA编程解决数位和相等问题
如果一个正整数转化成二进制与转换成八进制后所有数位的数字之和相等,则称为数位和相等的数。 前几个数位和相等的正整数为 1, 8, 9, 64, …… 请问第 23 个数位和相等的正整数是多少?用JAVA编程解决 可以通过编程计算第 23 个数位和相等的正整…...
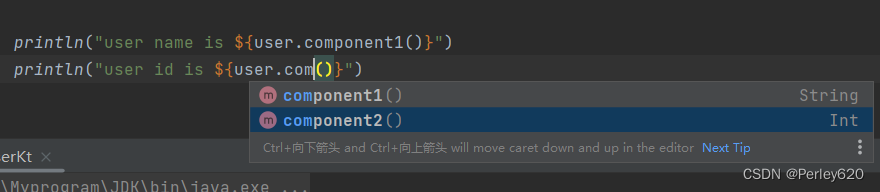
Kotlin学习——kt中的类,数据类 枚举类 密封类,以及对象
Kotlin 是一门现代但已成熟的编程语言,旨在让开发人员更幸福快乐。 它简洁、安全、可与 Java 及其他语言互操作,并提供了多种方式在多个平台间复用代码,以实现高效编程。 https://play.kotlinlang.org/byExample/01_introduction/02_Functio…...

XUbuntu22.04之解决gpg keyserver receive failed no data(一百九十三)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 人生格言: 人生…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...
