【代码随想录刷题】Day18 二叉树05

文章目录
- 1.【513】找树左下角的值
- 1.1题目描述
- 1.2 解题思路
- 1.2.1 迭代法思路
- 1.2.2 递归法思路
- 1.3 java代码实现
- 1.3.1 迭代法java代码实现
- 1.3.2 递归法java代码实现
- 2. 【112】路径总和
- 2.1题目描述
- 2.2 解题思路
- 2.3 java代码实现
- 3.【106】从中序与后序遍历序列构造二叉树
- 3.1题目描述
- 3.2 解题思路
- 3.3 java代码实现
【513】找树左下角的值
【112】路径总和
【106】从中序与后序遍历序列构造二叉树
1.【513】找树左下角的值
1.1题目描述
给定一个二叉树的 根节点 root,请找出该二叉树的 最底层 最左边 节点的值。
假设二叉树中至少有一个节点。
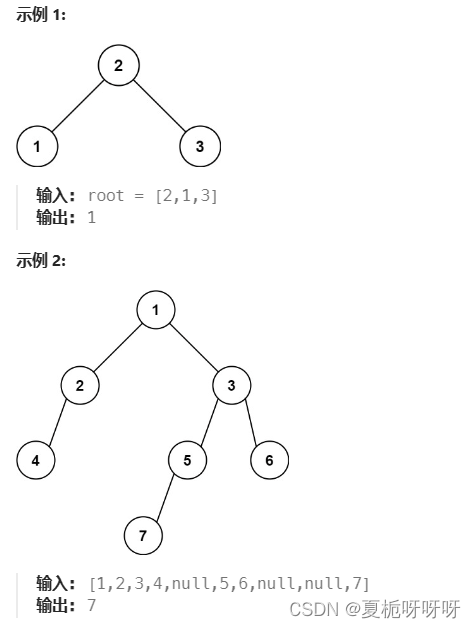
提示:
- 二叉树的节点个数的范围是 [1,104]
- -231 <= Node.val <= 231 - 1
1.2 解题思路
1.2.1 迭代法思路
本题要找出树的最后一行的最左边的值,使用层序遍历是非常简单的,只需要记录最后一行第一个节点的数值就可以了。
1.2.2 递归法思路
题目:在树的最后一行找到最左边的值。
首先要是最后一行,然后是最左边的值。
如果使用递归法,如何判断是最后一行呢?其实就是深度最大的叶子节点一定是最后一行。所以要找深度最大的叶子节点。
那么如何找最左边的呢?可以使用前序遍历(当然中序,后序都可以,因为本题没有 根节点的处理逻辑,只要左优先就行),保证优先左边搜索,然后记录深度最大的叶子节点,此时就是树的最后一行最左边的值。
递归三部曲
-
- 确定递归函数的参数和返回值
参数必须有要遍历的树的根节点,还有就是一个int型的变量用来记录最长深度。 这里就不需要返回值了,所以递归函数的返回类型为void。
本题还需要类里的两个全局变量,maxDepth用来记录最大深度,result记录最大深度最左节点的数值。
int result;// 全局变量 记录最大深度int maxDepth=-1;// 全局变量 最大深度最左节点的数值public void traversal(TreeNode root,int depth)
-
- 确定终止条件
当遇到叶子节点的时候,就需要统计一下最大的深度了,所以需要遇到叶子节点来更新最大深度。
if (root.left==null && root.right==null){if (depth>maxDepth){maxDepth=depth;// 更新最大深度result=root.val;// 最大深度最左面的数值}return;}
-
- 确定单层递归的逻辑
在找最大深度的时候,递归的过程中依然要使用回溯
if (root.left!=null){//左depth++;traversal(root.left,depth);//回溯depth--;}if (root.right!=null){//右depth++;traversal(root.right,depth);//回溯depth--;}return;
1.3 java代码实现
1.3.1 迭代法java代码实现
class Solution {public int findBottomLeftValue(TreeNode root) {//迭代法 层次遍历Queue<TreeNode> que=new LinkedList<>();que.offer(root);int res=0;while (!que.isEmpty()){int len=que.size();for (int i = 0; i < len; i++) {TreeNode tempNode=que.poll();// 记录最后一行第一个元素if (i==0){res=tempNode.val;}if (tempNode.left!=null){que.offer(tempNode.left);}if (tempNode.right!=null){que.offer(tempNode.right);}}}return res;}
}
1.3.2 递归法java代码实现
class Solution {int result;// 全局变量 记录最大深度int maxDepth=-1;// 全局变量 最大深度最左节点的数值public int findBottomLeftValue(TreeNode root) {//递归traversal(root,0);return result;}public void traversal(TreeNode root,int depth){if (root.left==null && root.right==null){if (depth>maxDepth){maxDepth=depth;// 更新最大深度result=root.val;// 最大深度最左面的数值}return;}if (root.left!=null){//左depth++;traversal(root.left,depth);//回溯depth--;}if (root.right!=null){//右depth++;traversal(root.right,depth);//回溯depth--;}return;}
}
递归函数简写:
public void traversal(TreeNode root,int depth){if (root.left==null && root.right==null){if (depth>maxDepth){maxDepth=depth;// 更新最大深度result=root.val;// 最大深度最左面的数值}return;}if (root.left!=null){//左traversal(root.left,depth+1);// 隐藏着回溯}if (root.right!=null){//右traversal(root.right,depth+1);// 隐藏着回溯}return;}
2. 【112】路径总和
2.1题目描述
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。
叶子节点 是指没有子节点的节点。
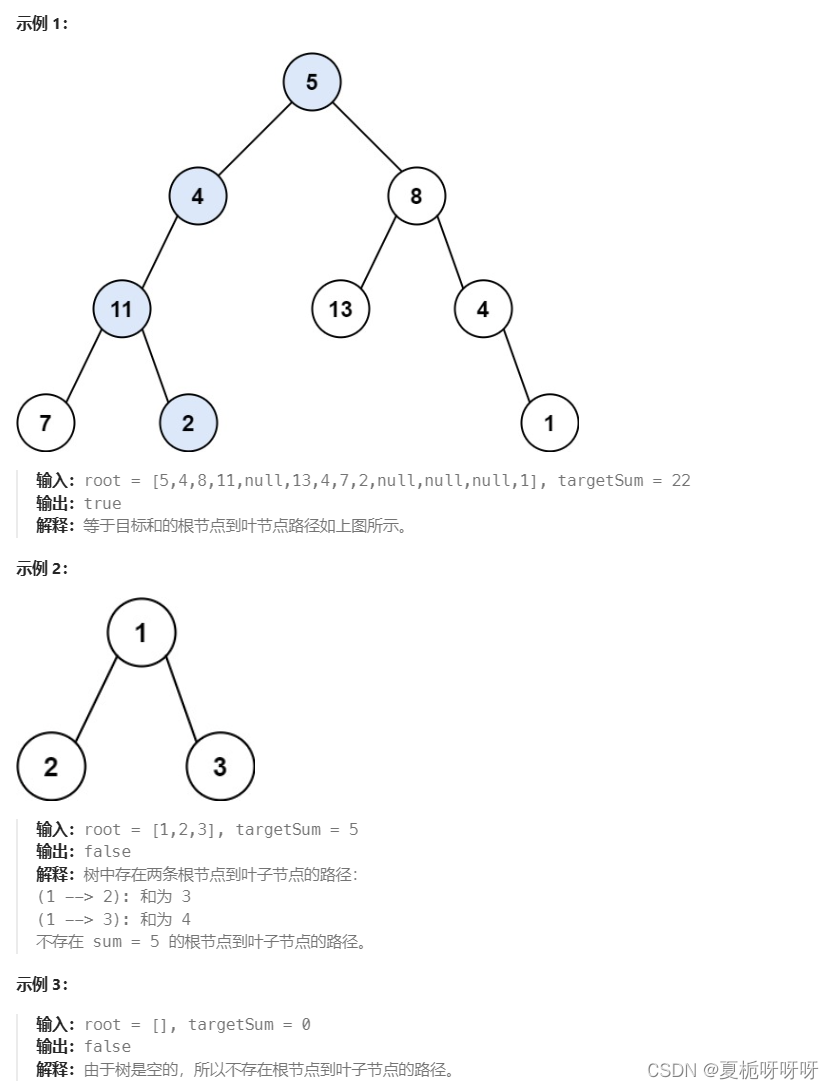
提示:
- 树中节点的数目在范围 [0, 5000] 内
- -1000 <= Node.val <= 1000
- -1000 <= targetSum <= 1000
2.2 解题思路
本题可以采用深度遍历的方式来遍历(本题前中后序都可以,无所谓,因为根节点也没有处理逻辑)。,递归法
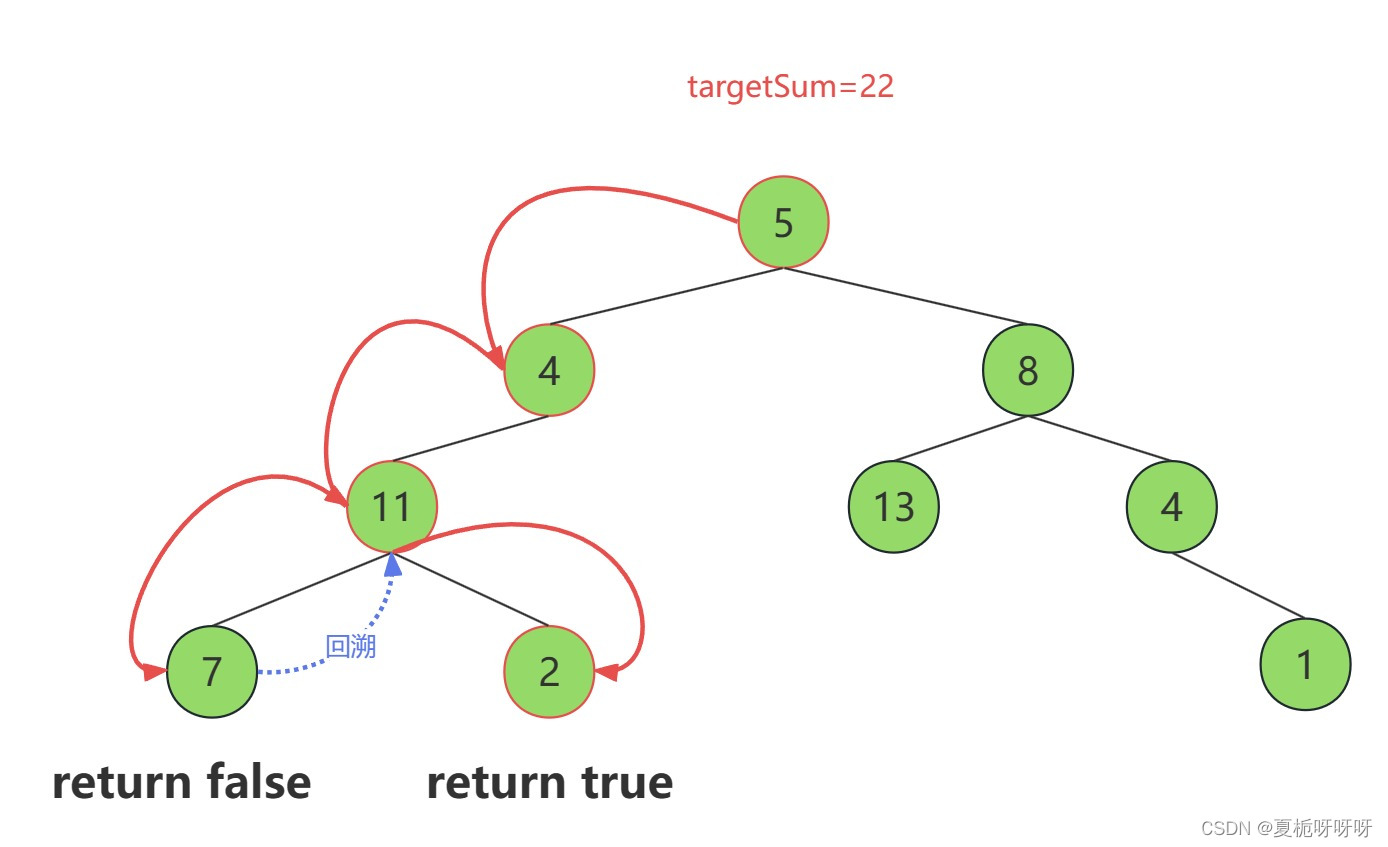
2.3 java代码实现
class Solution {public boolean hasPathSum(TreeNode root, int targetSum) {if (root==null){return false;}targetSum -= root.val;//叶子结点if (root.left==null && root.right==null){return targetSum==0;}if (root.left!=null){boolean left=hasPathSum(root.left,targetSum);//已经找到if (left){return true;}}if (root.right!=null){boolean right=hasPathSum(root.right,targetSum);//已经找到if (right){return true;}}return false;}
}
3.【106】从中序与后序遍历序列构造二叉树
3.1题目描述
给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。
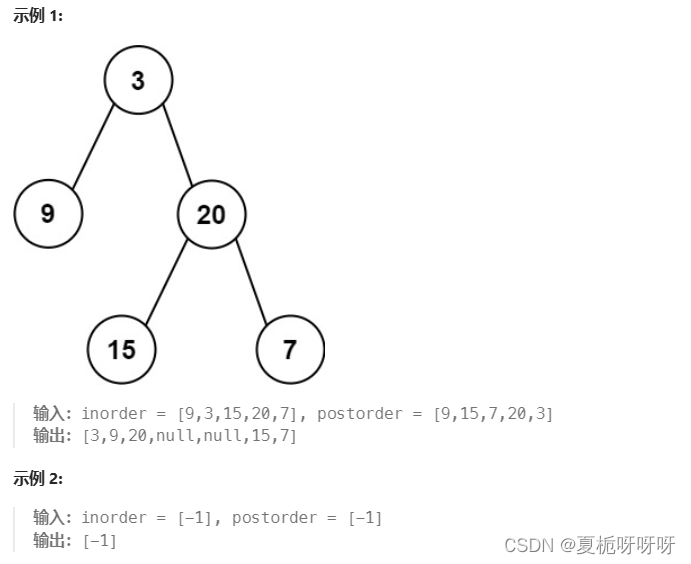
提示:
- 1 <= inorder.length <= 3000
- postorder.length == inorder.length
- -3000 <= inorder[i], postorder[i] <= 3000
- inorder 和 postorder 都由 不同 的值组成
- postorder 中每一个值都在 inorder 中
- inorder 保证是树的中序遍历
- postorder 保证是树的后序遍历
3.2 解题思路
中序遍历与后序遍历构造二叉树的理论知识
以 后续数组的最后一个元素为切割点,先切中序数组,根据中序数组,反过来再切后续数组。一层一层的切下去,每次后续数组的最后一个元素就是节点元素。
流程如下:
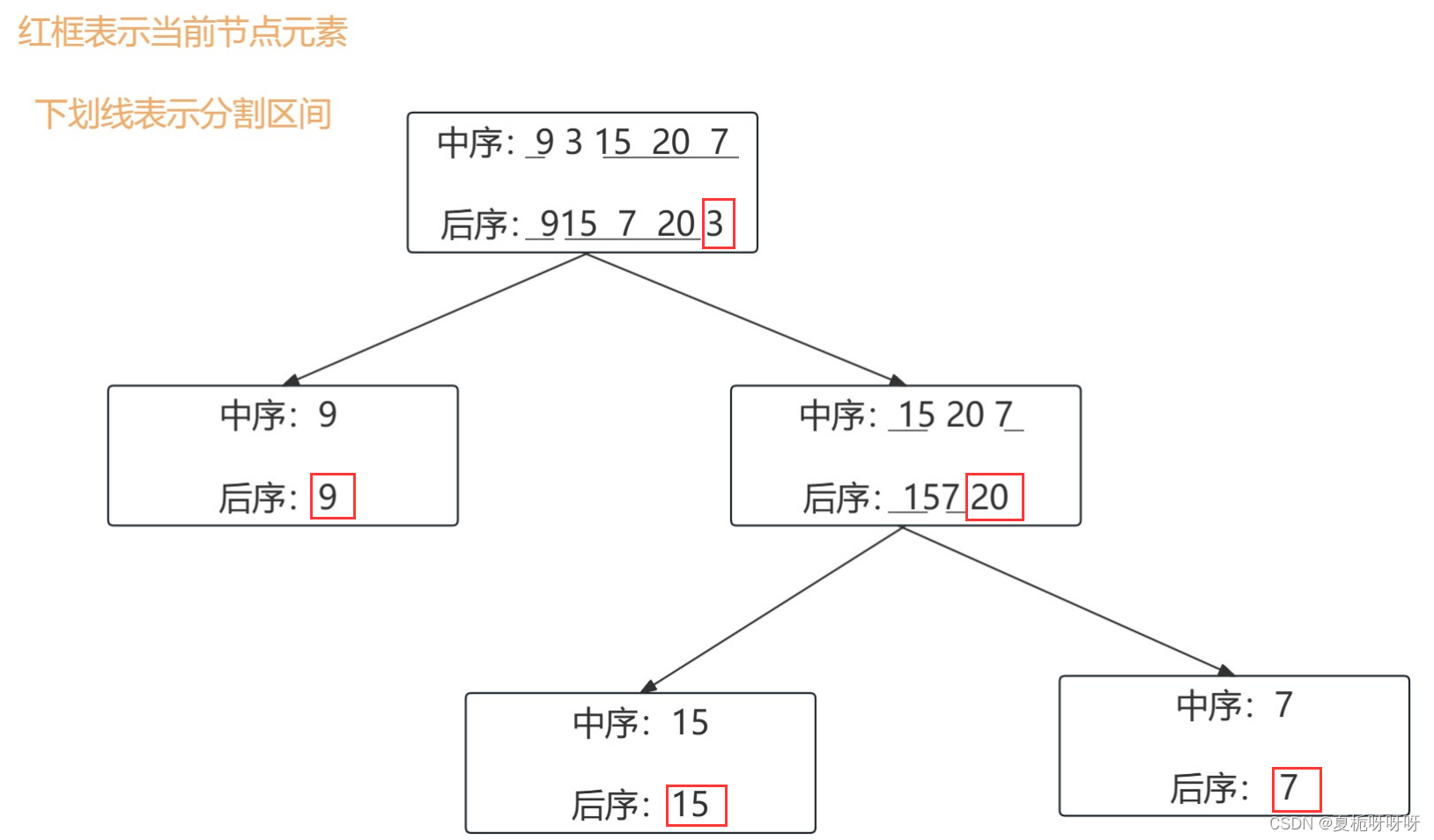
代码该怎样写呢?提到一层一层切割,就应该想到了递归
-
- 如果数组大小为0的话,说明是空节点了
-
- 如果不为空,那么取后序数组的最后一个元素作为节点元素
-
- 找到后序数组最后一个元素在中序数组中的位置,作为切割点
-
- 切割中序数组,切成中序左数组和中序右数组(顺序一定不能弄反了,一定要先切中序数组)
-
- 切割后序数组,切成后序左数组和后序右数组
-
- 递归处理左区间和右区间
3.3 java代码实现
class Solution {public TreeNode buildTree(int[] inorder, int[] postorder) {if (postorder.length==0 || inorder.length==0){return null;}return buildHelper(inorder,0,inorder.length,postorder,0, postorder.length);}public TreeNode buildHelper(int[] inorder,int inorderBegin,int inorderEnd,int[] postorder,int postBegin,int postEnd){if (postBegin==postEnd){return null;}//根节点int rootVal=postorder[postEnd-1];TreeNode root=new TreeNode(rootVal);//切割点int middleIndex;for (middleIndex=inorderBegin;middleIndex<inorderEnd;middleIndex++){if (inorder[middleIndex]==rootVal){break;}}//切割中序数组//左中序数组,左闭右开[leftInorderBegin,leftInoderEnd)int leftInorderBegin=inorderBegin;int leftInoderEnd=middleIndex;//右中序数组,左闭右开[rightInorderBegin,leftInoderEnd)int rightInorderBegin=middleIndex+1;int rightInoderEnd=inorderEnd;//切割后序数组//左后序数组,左闭右开[leftPostorderBegin,leftPostoderEnd)int leftPostorderBegin=postBegin;//终止位置是 需要加上 中序区间的大小sizeint leftPostoderEnd=postBegin+(middleIndex-inorderBegin);//右后序数组,左闭右开[rightPostorderBegin,leftPostoderEnd)int rightPostorderBegin=leftPostoderEnd;int rightPostoderEnd=postEnd-1;//排除最后一个元素,已经作为节点了root.left=buildHelper(inorder,leftInorderBegin,leftInoderEnd,postorder,leftPostorderBegin,leftPostoderEnd);root.right=buildHelper(inorder,rightInorderBegin,rightInoderEnd,postorder,leftPostorderBegin,rightPostoderEnd);return root;}
}
class Solution {Map<Integer,Integer> map;//方便根据数值查找位置public TreeNode buildTree(int[] inorder, int[] postorder) {map=new HashMap<>();// 用map保存中序序列的数值对应位置for (int i=0;i<inorder.length;i++){map.put(inorder[i],i );}return findNode(inorder,0,inorder.length,postorder,0,postorder.length);}public TreeNode findNode(int[] inorder,int inorderBegin,int inorderEnd,int[] postorder,int postBegin,int postEnd){//参数里的范围都是左闭右开if (inorderBegin>=inorderEnd || postBegin>=postEnd){return null;}// 找到后序遍历的最后一个元素在中序遍历中的位置int rootIndex=map.get(postorder[postEnd-1]);TreeNode root=new TreeNode(inorder[rootIndex]);//构造节点//保存中序左子树个数,用来确定后序数列的个数int lenOfleft=rootIndex-inorderBegin;root.left=findNode(inorder,inorderBegin,rootIndex,postorder,postBegin,postBegin+lenOfleft);root.right=findNode(inorder,rootIndex+1,inorderEnd,postorder,postBegin+lenOfleft,postEnd-1);return root;}}
相关文章:

【代码随想录刷题】Day18 二叉树05
文章目录 1.【513】找树左下角的值1.1题目描述1.2 解题思路1.2.1 迭代法思路1.2.2 递归法思路 1.3 java代码实现1.3.1 迭代法java代码实现1.3.2 递归法java代码实现 2. 【112】路径总和2.1题目描述2.2 解题思路2.3 java代码实现 3.【106】从中序与后序遍历序列构造二叉树3.1题目…...
2023.11.25更新关于mac开发APP(flutter)的笔记与整理(实机开发一)
我自己写的笔记很杂,下面的笔记是我在chatgpt4的帮助下完成的,希望可以帮到正在踩坑mac开发APP(flutter)的小伙伴 目标:通过MAC电脑使用flutter框架开发一款适用于苹果手机的一个APP应用 本博客的阅读顺序是…...

万宾科技可燃气体监测仪的功能有哪些?
随着城市人口的持续增长和智慧城市不断发展,燃气作为一种重要的能源供应方式,已经广泛地应用于居民生活和工业生产的各个领域。然而燃气泄漏和安全事故的风险也随之增加,对城市的安全和社会的稳定构成了潜在的威胁。我国燃气管道安全事故的频…...

Binlog vs. Redo Log:数据库日志的较劲【高级】
🎏:你只管努力,剩下的交给时间 🏠 :小破站 Binlog vs. Redo Log:数据库日志的较劲【高级】 前言第一:事务的生命周期事务的生命周期Binlog和Redo Log记录事务的一致性和持久性Binlog的记录过程R…...
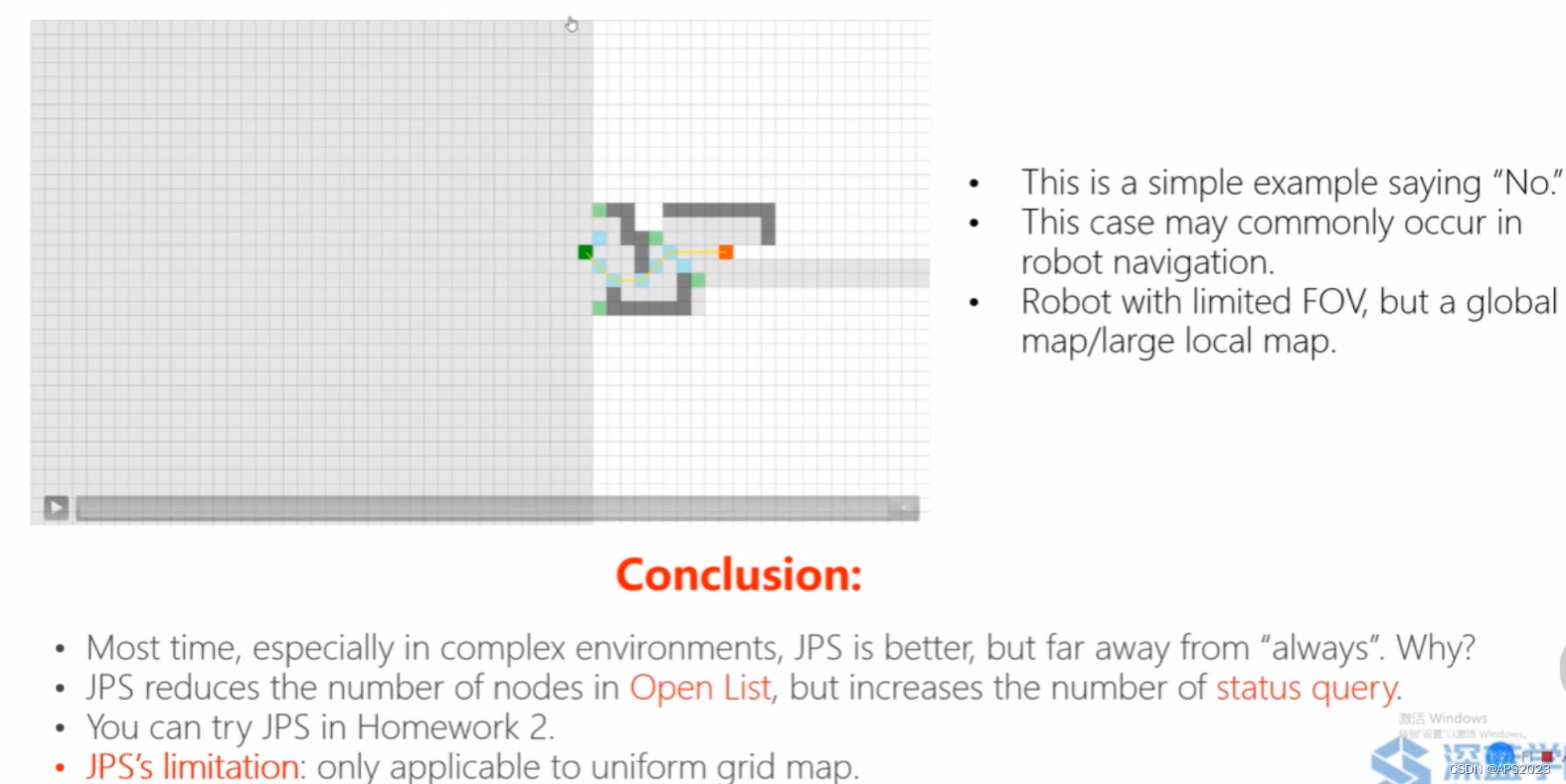
移动机器人路径规划(二)--- 图搜索基础,Dijkstra,A*,JPS
目录 1 图搜索基础 1.1 机器人规划的配置空间 Configuration Space 1.2 图搜索算法的基本概念 1.3 启发式的搜索算法 Heuristic search 2 A* Dijkstra算法 2.1 Dijkstra算法 2.2 A*&&Weighted A*算法 2.3 A* 算法的工程实践中的应用 3 JPS 1 图搜索基础 1.1…...
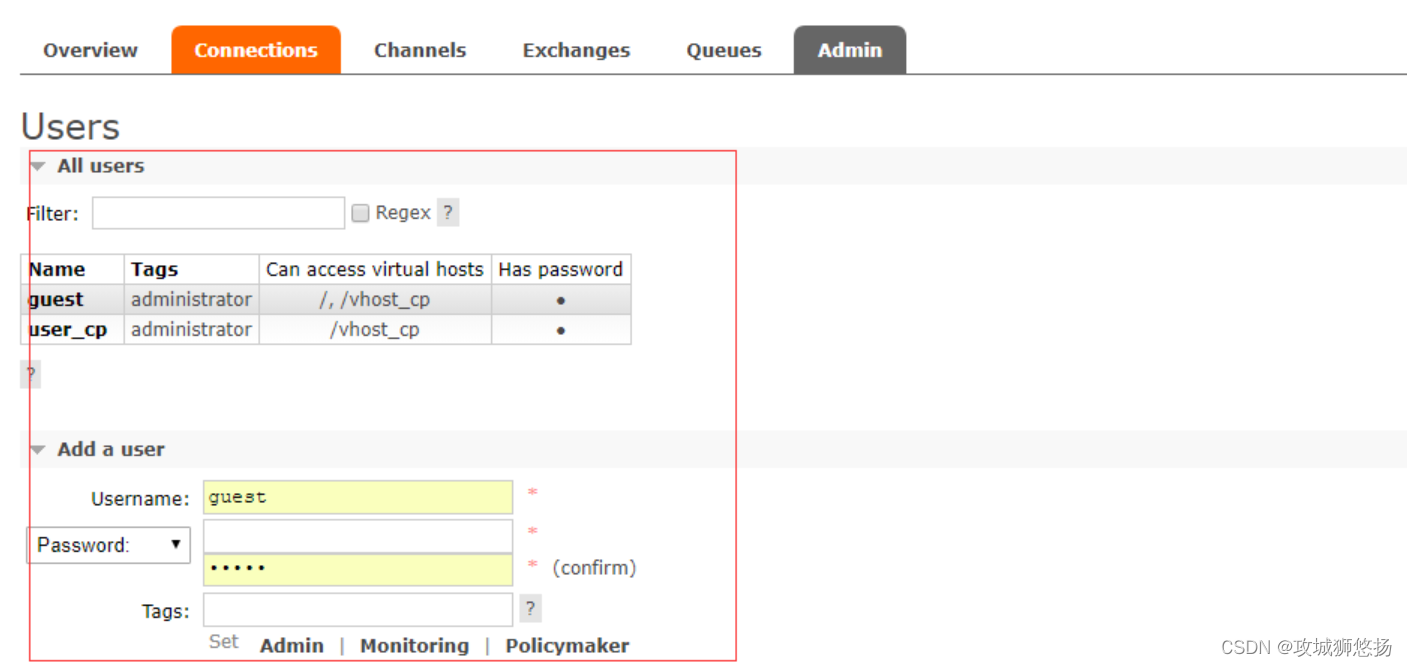
消息中间件——RabbitMQ(四)命令行与管控台的基本操作!
前言 在前面的文章中我们介绍过RabbitMQ的搭建:RabbitMQ的安装过以及各大主流消息中间件的对比:,本章就主要来介绍下我们之前安装的管控台是如何使用以及如何通过命令行进行操作。 1. 命令行操作 1.1 基础服务的命令操作 rabbitmqctl sto…...

性能压测工具:wrk
一般我们压测的时候,需要了解衡量系统性能的一些参数指标,比如。 1、性能指标简介 1.1 延迟 简单易懂。green:一般指响应时间 95线:P95。平均100%的请求中95%已经响应的时间 99线:P99。平均100%的请求中99%已经响应的时间 平…...
[Matlab有限元分析] 2.杆单元有限元分析
1. 一维杆单元有限元分析程序 一维刚单元的局部坐标系(单元坐标系)与全局坐标系相同。 1.1 线性杆单元 如图所示是一个杆单元,由两个节点i和j,局部坐标系的X轴沿着杆的方向,由i节点指向j节点,每个节点有…...
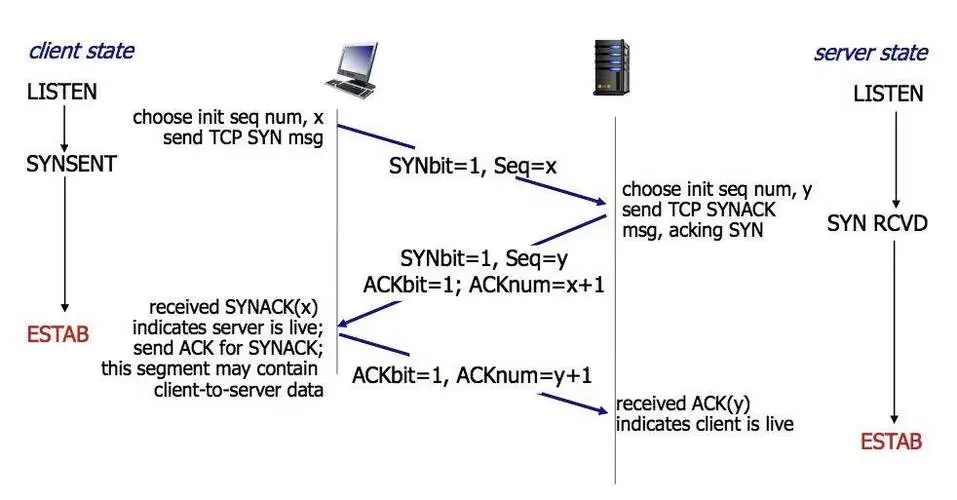
透过对话聊天聊网络tcp三次握手四次挥手
序 说起来网络,就让我想起的就是一张图。我在网上可以为所欲为,反正你又不能顺着网线来打我。接下来我们来详细说一下网络到底是怎么连接的。 TCP三次打招呼 首先我会用男女生之间的聊天方式,来举一个例子。 从tcp三次握手来说,…...
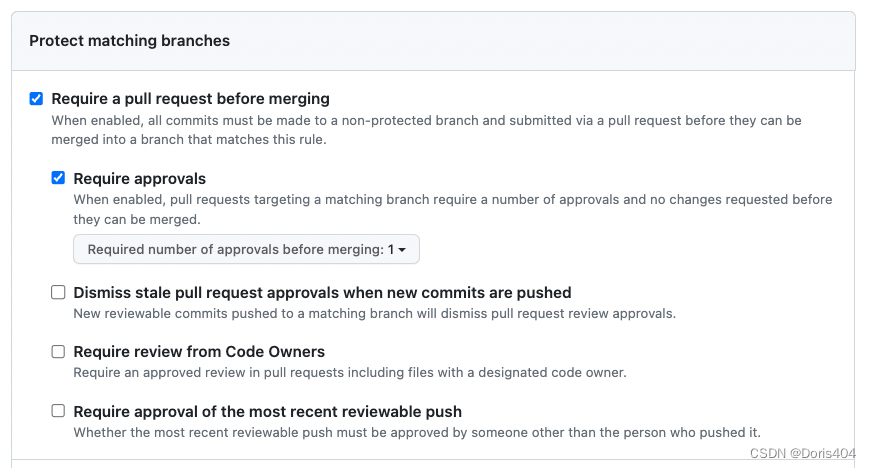
项目管理套路:看这一篇绝对够用❤️
写论文必不可少的,就是创建代码并进行实验。好的项目管理可以让实验进行得更加顺利。本篇博客以一次项目实践为例,介绍项目管理的方法,以及可能遇到的问题,并提供一些可行的解决方案。 目录 项目管理工具开始第一步版本管理十分关…...

华为-算法---测试开发工程师----摘要牛客网
Java面试题---摘要牛客网-CSDN博客package extendNiuKeWang;import java.util.Scanner;public class GoodHuaWei {public static void main(String[] args) {Scanner sc = new Scanner(System.in);int money = sc.nextInt();System.out.println("n值总金额:"+money)…...
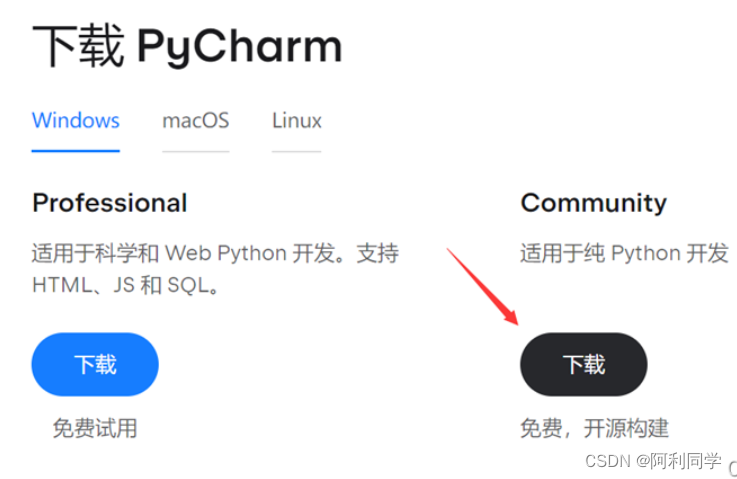
python环境搭建-yolo代码跑通-呕心沥血制作(告别报错no module named torch)
安装软件 安装过的可以查看有没有添加环境变量 好的! 我们发车! 如果你想方便快捷的跑通大型项目,那么必须安装以下两个软件: 1.pycharm2.anaconda对应作用: pycharm:专门用来跑通python项目的软件,相当于一个编辑器,可以debug调试,可以接受远程链接调试!anaconda:专…...
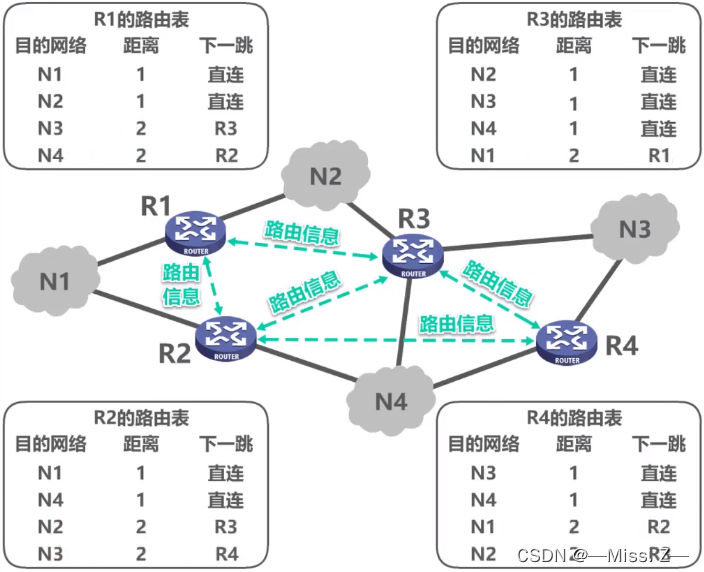
Cisco Packet Tracer配置命令——路由器篇
路由基础 路由器用于互联两个或多个网络,具有两项功能:为要转发的数据包选择最佳路径以及将数据包交换到正确的端口,概括为路由选择和分组转发。 路由选择 路由选择就是路由器根据目的IP地址的网络地址部分,通过路由选择算法确…...
) 是 QWidget 类的成员函数,用于设置小部件的内容边距(Contents Margins))
setContentsMargins(QMargins()) 是 QWidget 类的成员函数,用于设置小部件的内容边距(Contents Margins)
setContentsMargins(QMargins()) 是 QWidget 类的成员函数,用于设置小部件的内容边距(Contents Margins)。 在 Qt 中,内容边距指的是小部件内部内容与小部件边界之间的空白区域。通过设置内容边距,可以控制和调整小部…...

Redis key 过期监听实现
1.技术背景,想知道 redis 设置了TTL时间的key 过期,且有后续的业务处理的场景可以使用。 bug点: 使用redis 缓存失效监听会有一定的延迟, 过期事件是在redis服务器删除键的时候生成的,而不是在理论上生存时间到达0值得…...
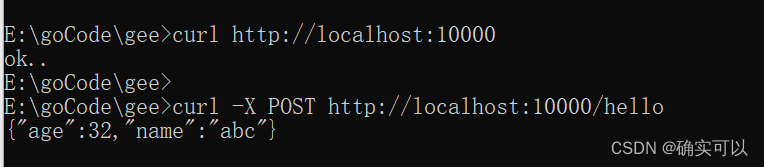
Gee教程2.上下文Context
先来看看Gin框架的简单例子 func main() {engine : gin.Default()engine.GET("/", func(c *gin.Context) {c.String(http.StatusOK, "hello World!")})//监听并启动服务,默认 http://localhost:8080/engine.Run() }//我们自己写的 func main()…...
【从浅识到熟知Linux】基本指定之cat、more和less
🎈归属专栏:从浅学到熟知Linux 🚗个人主页:Jammingpro 🐟每日一句:写完这篇我要去吃晚饭啦!! 文章前言:本文介绍cat、more和less指令三种查看文件的用法并给出示例和截图…...

2018年7月24日 Go生态洞察:Go Cloud实现便携式云编程
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...
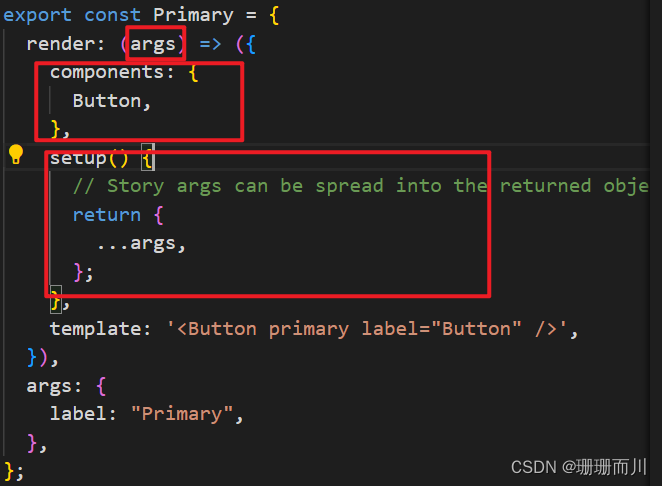
storyBook常见踩坑报错 和 解决
用StoryBook官网的代码,但报错,Unexpected token’<’ 在js文件中// Button.stories.js|jsx import { Button } from ‘./Button’; export default { component: Button, }; /* *👇 Render functions are a framework specific featur…...

python 笔记 根据用户轨迹+基站位置,估计基站轨迹+RSRP
1 问题描述 已知用户实际的轨迹,和基站的位置,能不能得到用户所连接的基站,以及基站的信号强度RSRP? 1.1 几个假设 这里我们做几个假设: 每个用户有80%的概率连接最近的基站,有20%的概率选择其他的基站连…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...
