2017年五一杯数学建模B题自媒体时代的消息传播问题解题全过程文档及程序
2017年五一杯数学建模
B题 自媒体时代的消息传播问题
原题再现
电视剧《人民的名义》中人物侯亮平说:“现在是自媒体时代,任何突发性事件几分钟就传播到全世界。”相对于传统媒体,以互联网技术为基础的自媒体以其信息传播的即时性、交往方式的平等性和交往身份的虚拟性等特点,已经成为公民获取信息、表达情感与思想、参与社会公共生活的重要载体,并逐渐渗透到政治、经济、文化、社会等诸多领域。
结合实际情况,建立数学模型,解决以下问题:
问题 1:建立一条消息在自媒体平台上传播的数学模型,并以“中共中央、国务院决定设立河北雄安新区”这条消息为例,分析其传播过程。
问题 2:某条消息在自媒体传播的过程中,如果出现了新的与之高度关联的消息(例如相关单位或知名人士发布了新的消息),建立数学模型,分析并说明新消息出现后传播过程的变化情况。
问题 3:请建立数学模型分析(1)不同类型的消息在自媒体传播过程中是否存在差异?(2) 同一消息在不同自媒体平台上传播是否存在差异?并通过数值算例进行验证。
问题 4:结合所建立的模型,写一份分析报告,阐述你对自媒体时代消息传播的见解或看法,并进一步提出自媒体平台管理的建议。
整体求解过程概述(摘要)
新媒体的诞生标志着信息的传递进入了一个全新的时代,各类信息间的相互渗透,媒体平台间的交叉传递,拉近人与人间的距离,无时无刻地影响着人们生活方式。
本文就信息的传递方式及过程展开研究,主要解决了信息如何在实际生活中传递的问题,并针对与之高度关联信息出现时的对其传播带来的影响,给出了其最优化影响的处理方案,同时考虑信息自身的类型及媒体平台的差异,结合数据分别分析了其各自影响,最后依据所得结论,提出了一份关于新媒体消息传播及管理的报告。
针对问题一,我们基于传统传染病传播模型,就 SNS 网络建立一种新型 SEIR模型,将消息传播过程中不同职能的媒体平台化作不同节点,分别分析其在实际传播过程中的变化过程,多角度地揭示了实际消息传播的过程。
针对问题二,依据高度相似消息的出现,我们沿用问题一传染病传播的思想,建立基于节点属性和信息内容等多个因素,对信息传播概率和传播延迟两个目标变量建立细粒度的模型,具体分析了新消息对原消息传播带来的影响并求解出最大化影响的条件。
针对问题三,我们建立元胞自动机模型仿真不同信息类型对传播带来的影响,并给出两者间的关系,结果表明受用户欢迎度高的消息具备更广泛的辐射范围及更快的传播速率。对于不同类型的媒体平台,我们建立一种新型 LWCS 模型考量平台类型与消息传播的关系,经数据分析得出平台的类型仅与传播过程中速率相关,同时我们还证明了该指标相对于其他指标的正确性及优越性。
针对问题四,我们梳理前三问中所得结论,就自媒体平台管理的现状,给出切实可行的改进建议。
模型假设:
1.假设在某条消息传播过程不受自然因素影响;
2.假设消息传播过程不受政策的影响;
3.假设各个自媒体平台之间相互独立;
4.假设不同类型信息间不存在竞争;
5.假设网络中每个节点本身具有一定的权重。
问题分析:
问题一的分析
新媒体时代的信息传播的不是简单的图论网络,还要实际情况,显然鉴于信息的特殊性质,可以将信息类比于流行性传染疾病的传播。但这还是远远不够的,所以在此基础上我们建立一种新型的 SEIR 模型,更加细分传播过程中媒体平台的职能,最后利用 MATLAB 对设立的偏微分方程进行求解。
问题二的分析
为探究新高度关联消息对原信息的影响,我们必须先分析新信息的特征,为此,沿用问题一的思想我们建立了基于节点和信息传播特征的网络信息的传播模型,鉴于问题二的情况提取出两个主影响因子,得出节点间传播速率与新信息的关系,并利用问题一中的模型得出了节点间传播速率与整体信息传播点密度的关系,进行分析比较可得出影响其重要因素。
问题三的分析
针对不同类型的数据,必然有着不同的节点传播速率,在此基础上我们利用元胞自动机进行仿真,改变每次仿真时的节点传播速率,并对数据数据分析。对于不同类型的媒体平台,我们没有选用传统的单一指标,而是建立了一符合LWCS 模型作为评价标准,我们利用问题一中的模型对其进行检验的一方面验证了其正确性,另一方面证明其较与其他指标的优越性,并利用所得的结果进行分析。
问题四的分析
对于问题四,可根据前三个问题所建立的模型及其结论,针对其存在的问题对自媒体平台管理提出切实可行的建议。
模型的建立与求解整体论文缩略图

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
程序代码:(代码和文档not free)
function y=prsir(t,x,theta,eta,alpha,k)
theta=0.5;lambda=0.5;h=2;d=0.5;
eta=theta*(1-(1-lambda).^(h*d));
w=0.5;rho=2;epsilon=1;
alpha=w./(1+exp(rho-epsilon*t));
k=14;
y=[-theta*k*x(1)*x(2),eta*k*x(1)*x(2)-alpha*k*x(2)*(x(2)+x(3)),al
pha*k*x(2)*(x(2)+x(3))+(theta-eta)*k*x(1)*x(2)]';
% Command Window
ts=0:0.5:10;
x0=[4999/5000,1/5000,0];
[t,x]=ode45('prsir',ts,x0);[t,x]
plot(t,x(:,1),'rs-',t,x(:,2),'b*-',t,x(:,3),'go-'),grid,
xlabel('t');ylabel('PR-SIR模型中三类节点密度
');legend('I(t)','S(t)','R(t)');
title('\theta=0.5,\lambda=0.5,h=2,d=0.5,w=0.5,\rho=2,\epsilon=1')
分析 d 变化对传播节点的影响:
% prsira.m
function y=prsira(t,x,theta,eta,alpha,k)
w=0.5;rho=2;epsilon=1;
alpha=w./(1+exp(rho-epsilon*t));
y=[-theta*k*x(1)*x(2),eta*k*x(1)*x(2)-alpha*k*x(2)*(x(2)+x(3)),al
pha*k*x(2)*(x(2)+x(3))+(theta-eta)*k*x(1)*x(2)]';
% Command Window
ts=0:0.5:10;
theta=0.5;
lambda=0.5;
h=2;
d=0.2;
eta=theta*(1-(1-lambda).^(h*d));
k=14;
x0=[4999/5000,1/5000,0];
[t,x]=ode45(@(t,x) prsira(t,x,theta,eta,alpha,k),ts,x0);[t,x]
plot(t,x(:,2),'g*-'),grid,
hold on
ts=0:0.5:10;
theta=0.5;
lambda=0.5;
h=2;
d=0.4;
eta=theta*(1-(1-lambda).^(h*d));
k=14;
x0=[4999/5000,1/5000,0];
[t,x]=ode45(@(t,x) prsira(t,x,theta,eta,alpha,k),ts,x0);[t,x]
plot(t,x(:,2),'r*-'),grid,
hold on
ts=0:0.5:10;
theta=0.5;
lambda=0.5;
h=2;
d=0.6;
eta=theta*(1-(1-lambda).^(h*d));
k=14;
x0=[4999/5000,1/5000,0];
[t,x]=ode45(@(t,x) prsira(t,x,theta,eta,alpha,k),ts,x0);[t,x]
plot(t,x(:,2),'c*-'),grid,
hold on
ts=0:0.5:10;
theta=0.5;
lambda=0.5;
h=2;
d=0.8;
eta=theta*(1-(1-lambda).^(h*d));
k=14;
x0=[4999/5000,1/5000,0];
[t,x]=ode45(@(t,x) prsira(t,x,theta,eta,alpha,k),ts,x0);[t,x]
plot(t,x(:,2),'m*-'),grid,
grid on
xlabel('t');ylabel('传播节点密度
S(t)');legend('d=0.2','d=0.4','d=06','d=0.8');
title('\theta=0.5,\lambda=0.5,h=2,w=0.5,\rho=2,\epsilon=1')
function y=prsir(t,x,theta,eta,alpha,k)
w=0.5;rho=2;epsilon=1;
alpha=w./(1+exp(rho-epsilon*t));
k=14;
y=[-theta*k*x(1)*x(2),eta*k*x(1)*x(2)-alpha*k*x(2)*(x(2)+x(3)),al
pha*k*x(2)*(x(2)+x(3))+(theta-eta)*k*x(1)*x(2)]';
% Command Window
ts1=0:0.5:2;
theta=0.5;lambda=0.5;h=2;d=0.5;
eta=theta*(1-(1-lambda).^(h*d));
x0=[4999/5000,1/5000,0];
[t,x]=ode45('prsir',ts1,x0);[t,x]
plot(t,x(:,2),'b*-','linewidth',2),grid,
hold on
ts2=2:0.5:8;
theta=0.5;lambda=0.5;h=4;d=0.5;
eta=theta*(1-(1-lambda).^(h*d));
x0=[4999/5000,1/5000,0];
[t,x]=ode45('prsir',ts2,x0);[t,x]
plot(t,x(:,2),'r*-','linewidth',2),grid,
grid on
xlabel('t');ylabel('传播节点密度S(t)');legend('h=2','h=4');
title('\theta=0.5,\lambda=0.5,d=0.5,w=0.5,\rho=2,\epsilon=1')
全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
相关文章:

2017年五一杯数学建模B题自媒体时代的消息传播问题解题全过程文档及程序
2017年五一杯数学建模 B题 自媒体时代的消息传播问题 原题再现 电视剧《人民的名义》中人物侯亮平说:“现在是自媒体时代,任何突发性事件几分钟就传播到全世界。”相对于传统媒体,以互联网技术为基础的自媒体以其信息传播的即时性、交往方式…...

虹科分享 | AR世界揭秘:从二维码的起源到数据识别与位姿技术的奇妙融合!
引言:探索AR的神奇世界,我们将从二维码的诞生谈起。在这个科技的海洋中,二维码是如何帮助AR实现数据获取与位姿识别的呢?让我们一起揭开这层神秘的面纱! 一、二维码的由来 二维码是将数据存储在图形中的技术ÿ…...

基于helm部署并配置StorageClass
此类方法适用于测试环境或者小型的集群环境,因为nfs是网络文件系统,在io性能上并不能有所保证。 前置条件: 已部署k8s集群已安装helm 工具 step1: 安装nfs服务 yum install nfs-utils -ystep2: 配置nfs # 编辑/etc/exports /data/nfs *(r…...

Python基础:字符串详解(需补充完善)
1. 字符串定义 在Python中,字符串是一种数据类型,用于表示文本数据。字符串是由字符组成的序列,可以包含字母、数字、符号和空格等字符。在Python中,你可以使用单引号()或双引号("&#x…...

做直播服务器要什么样的配置呢?
现在直播行业越来越火爆,大大小小的平台或者企业都选择通过直播卖货的方式出售产品,直播的内容还有观看直播的人数等等都影响了服务器的配置需求,今天小编就给大家讲一讲吧! 1、内存:直播服务器需要足够的内存才能支持…...

⑥【bitmap 】Redis数据类型: bitmap [使用手册]
个人简介:Java领域新星创作者;阿里云技术博主、星级博主、专家博主;正在Java学习的路上摸爬滚打,记录学习的过程~ 个人主页:.29.的博客 学习社区:进去逛一逛~ Redis bitmap ⑥Redis bitmap 基本操作命令1. …...

CentOS升级GCC
背景 CentOS 7默认自带GCC版本4.8,而目前工作中开发环境需要用到GCC8和GCC12,这里记录一下如何升级GCC版本,以及如何多版本并存。参考: CentOS升级gcc-知乎 Redhat7上安装Red Hat Developer Toolset并自由切换gcc和g的版本 Cent…...
CodeWhisperer 体验总结
CodeWhisperer 体验总结 | CodeWhisperer 是一款亚马逊新推出的通用代码生成器 可以实时进行代码数据的提供 还可以定义安全问题 CodeWhisperer 对个人用户是免费使用 企业用户需要订阅使用 亚马逊云科技开发者社区为开发者们提供全球的开发技术资源。这里有技术文档、开发案例…...
)
Apache换行解析漏洞(CVE-2017-15715)
漏洞简介 Apache換行解析漏洞(CVE-2017-15715)是一种解析漏洞,可以影响httpd 2.4.0至2.4.29版本中的PHP解析。攻击者可以通过在上传的文件名中添加特定的换行符,绕过服务器的安全策略,使其被解析成PHP文件而不是普通文件。此漏洞会影响具有以下条件的服务器: 未正确配置…...

人工智能时代的内容写作
内容不再只是王道,正如俗话所说:它是一种流动的货币,推动了巨大的在线信息和影响力经济。 每个品牌都是一个故事,通过其服务和商品讲述自己。尽管如此,大多数客户还是会通过您的在线内容最了解您。 但随着我们进入人…...
ASM字节码操作类库(打开java语言世界通往字节码世界的大门) | 京东云技术团队
前言:授人以鱼不如授人以渔,应用asm的文章有很多,简单demo的也很多,那么ASM都具备哪些能力呢?如何去学习编写ASM代码呢?什么样的情景需要用到ASM呢?让我们带着这些问题阅读这篇文章吧。 这里由…...
SpringBoot 拦截器高级篇
Springboot 拦截器 定义使用场景拦截器与过滤器的区别实现步骤全局拦截器的局限性全局拦截器VS局部拦截器局部拦截器自定义局部拦截器使用多个局部拦截器 定义 拦截器是Spring MVC框架中的一个重要组件,它是一种AOP(面向切面编程)的实现方式&…...
)
Android frameworks 开发总结之十(lock screen message Battery Last full charge)
1.設置lock screen message後不显示 XXXt設備設置lock screen message後,發現鎖頻界面不顯示內容,像時間日期都不顯示。只在右上角顯示一個鎖圖標,需要向下滑動一下才能顯示出來。布局文件位置: frameworks/base/packages/SystemUI/res-keygu…...

[建议收藏] 一个网站集合所有最新最全的AI工具
今天给大家推荐一个宝藏的AI工具合集网站,有了这个网站,你们再也不用去其他地方找AI工具了。 名称:AI-BOT工具集 这个网站精选1000AI工具,并持续每天更新添加,包括AI写作、AI绘画、AI音视频处理、AI平面设计、AI自动编…...

嵌入式硬件基础知识——1
目录 SOC、MCU、MPU、CPU SPI STM32的时钟系统 can是什么 串口和并口 传感器输出引脚高阻抗好还是低阻抗好? iic 运算放大器特点 MOS管和三极管 同步电路和异步电路 SOC、MCU、MPU、CPU SOC 片上系统 手机的核心芯片 MCU 微控系统 单片机 MPU 嵌入式微处…...

Spring如何在多线程下保持事务的一致性
Spring如何在多线程下保持事务的一致性 方法:每个线程都开启各自的事务去执行相关业务,等待所有线程的业务执行完成,统一提交或回滚。 下面我们通过具体的案例来演示Spring如何在多线程下保持事务的一致性。 1、项目结构 2、数据库SQL CR…...

外部中断为什么会误触发?
今天在写外部中断的程序的时候,发现中断特别容易受到干扰,我把手放在对应的中断引脚上,中断就一直触发,没有停过。经过一天的学习,找到了几个解决方法,所以写了这篇笔记。如果你的中断也时不时会误触发&…...
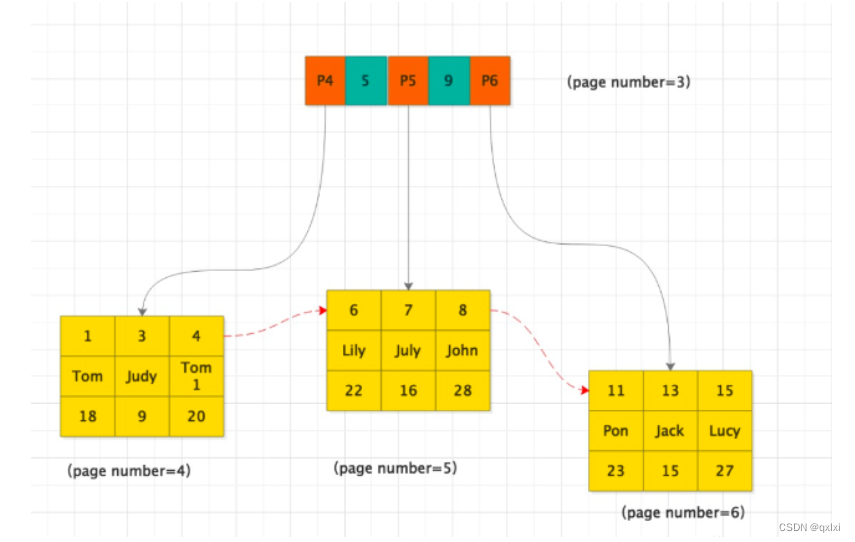
【数据库】聊聊一颗B+树 可以存储多少数据
我们知道数据库使用的数据结构是B树,但是B树可以存储多少数据呢,在面试中也是经常会问的问题,所以我们从根上理解这个问题。 操作系统层面 数据都是存储在磁盘中的,而磁盘中的数据都是以最新单位扇区进行分割。一个扇区的大小是…...

【机器学习 | ARIMA】经典时间序列模型ARIMA定阶最佳实践,确定不来看看?
🤵♂️ 个人主页: AI_magician 📡主页地址: 作者简介:CSDN内容合伙人,全栈领域优质创作者。 👨💻景愿:旨在于能和更多的热爱计算机的伙伴一起成长!!&…...
Python web自动化测试 —— 文件上传
文件上传三种方式: (一)查看元素标签,如果是input,则可以参照文本框输入的形式进行文件上传 方法:和用户输入是一样的,使用send_keys 步骤:1、找到定位元素,2&#…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...
