HTTP协议发展
HTTP 1.0 -> HTTP 1.1 -> HTTP 2.0 -> HTTP 3.0 (QUIC)
每一代HTTP解决了什么问题?
下图说明了主要功能。
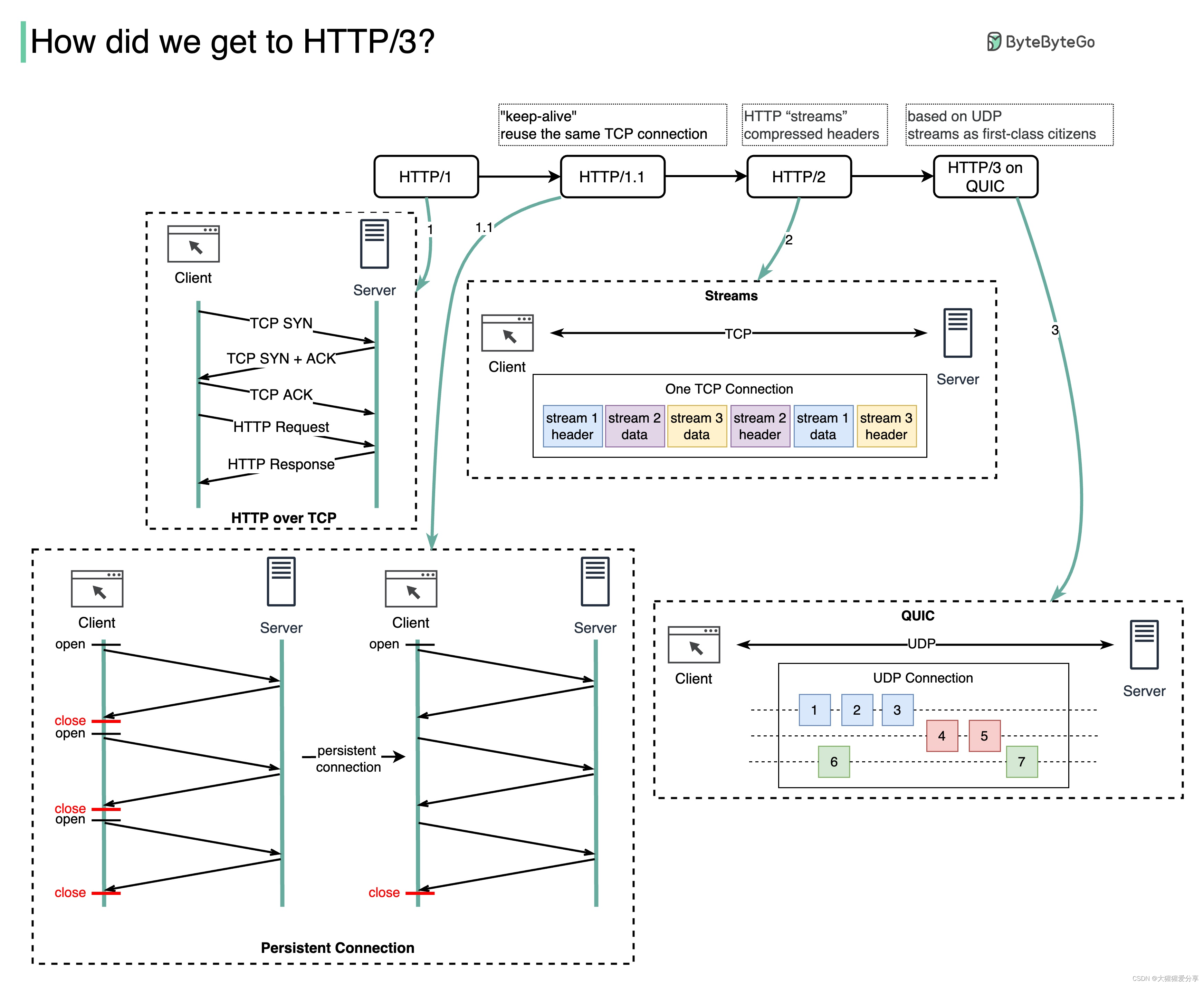
-
HTTP 1.0 于 1996 年最终确定并完整记录。对同一服务器的每个请求都需要单独的 TCP 连接。
-
HTTP 1.1 于 1997 年发布。TCP 连接可以保持打开状态以供重用(持久连接),但它并没有解决 HOL(队头)阻塞问题。
HOL阻塞——当浏览器允许的并行请求数用完时,后续请求需要等待前面的请求完成。
-
HTTP 2.0于2015年发布,通过请求复用解决了HOL问题,消除了应用层的HOL阻塞,但传输层(TCP)仍然存在HOL。
如图所示,HTTP 2.0 引入了 HTTP“流”的概念:一种允许将不同的 HTTP 交换复用到同一个 TCP 连接上的抽象。每个流不需要按顺序发送。
-
HTTP 3.0 第一稿于 2020 年发布。它是 HTTP 2.0 的拟议后继者。它使用 QUIC 而不是 TCP 作为底层传输协议,从而消除了传输层的 HOL 阻塞。
QUIC 基于 UDP。它将流作为传输层的一等公民引入。QUIC 流共享相同的 QUIC 连接,因此创建新流不需要额外的握手和缓慢启动,但 QUIC 流是独立交付的,因此在大多数情况下,影响一个流的数据包丢失不会影响其他流。
HTTP 状态代码
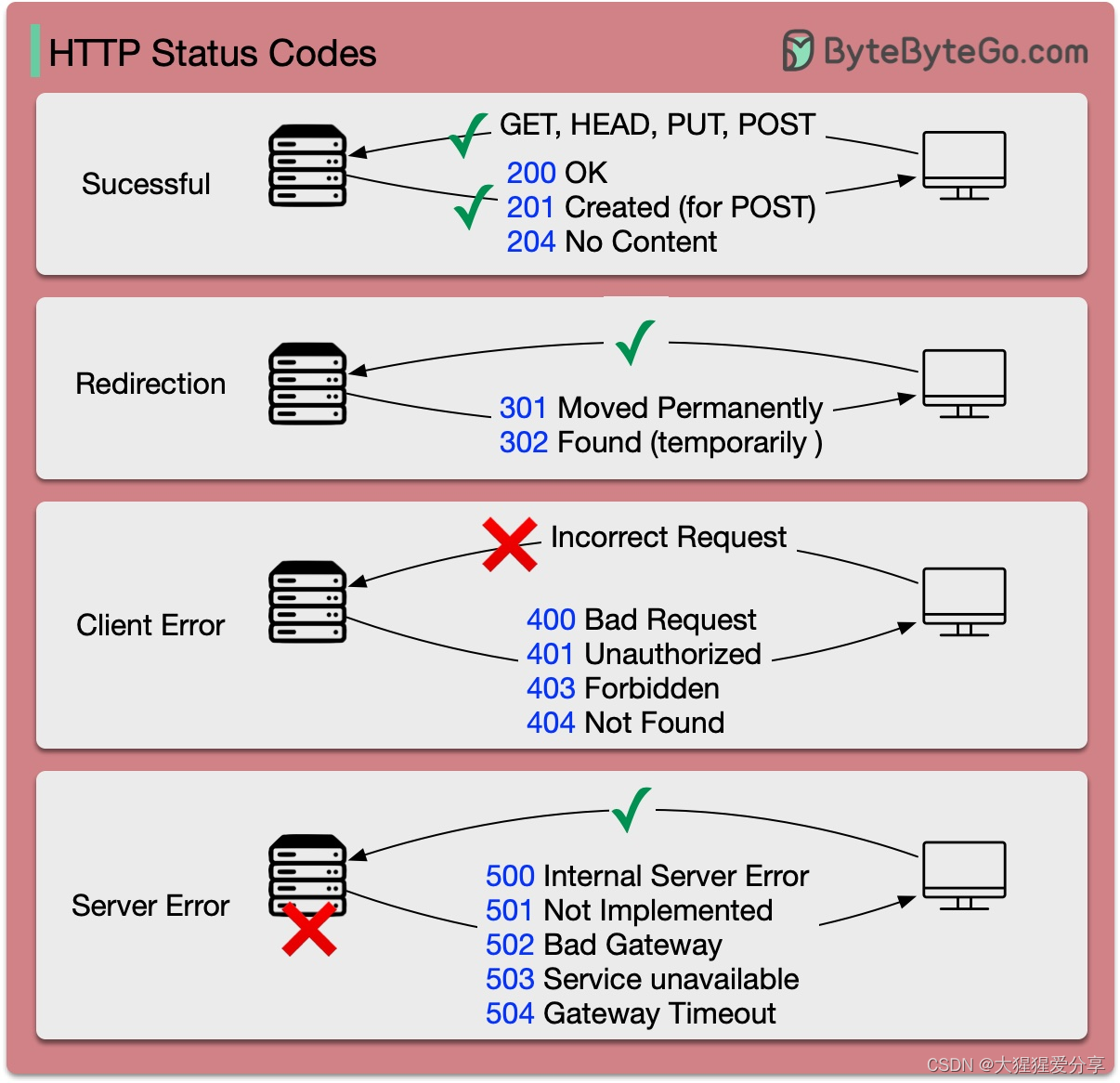
HTTP 的响应代码分为五类:
信息性 (100-199) 成功 (200-299) 重定向 (300-399) 客户端错误 (400-499) 服务器错误 (500-599)
相关文章:

HTTP协议发展
HTTP 1.0 -> HTTP 1.1 -> HTTP 2.0 -> HTTP 3.0 (QUIC) 每一代HTTP解决了什么问题? 下图说明了主要功能。 HTTP 1.0 于 1996 年最终确定并完整记录。对同一服务器的每个请求都需要单独的 TCP 连接。 HTTP 1.1 于 1997 年发布。TCP 连接可以保持打开状态…...

杰发科技AC7801——ADC软件触发的简单使用
前言 7801资料读起来不是很好理解,大概率是之前MTK的大佬写的。在此以简单的方式进行描述。我们做一个简单的规则组软件触发Demo。因为规则组通道只有一个数据寄存器,因此还需要用上DMA方式搬运数据到内存。 AC7801的ADC简介 7801的ADC是一种 12 位 逐…...

佳易王个体诊所门诊电子处方软件试用版下载,佳易王电子处方软件的配方模板功能作用与教程
佳易王个体诊所门诊电子处方软件试用版下载,佳易王电子处方软件的配方模板功能作用与教程 1、软件试用版及教程可以点击下方的官网卡片 2、软件中有一个实用的功能,配方模板功能,在开处方单时候可以一键导入配方,节省时间。 而…...

FFmpeg零基础学习(二)——视频文件信息获取
目录 前言正文一、获取宽高信息1、核心代码2、AVFormatContext3、avformat_alloc_context4、avformat_open_input5、avformat_find_stream_info6、av_dump_format7、av_find_best_stream End、遇到的问题1、Qt Debug模式avformat_alloc_context 无法分配对象,而Rele…...
探索 Vue 中的 bus.$emit:实现组件通信的强大工具
🤍 前端开发工程师(主业)、技术博主(副业)、已过CET6 🍨 阿珊和她的猫_CSDN个人主页 🕠 牛客高级专题作者、在牛客打造高质量专栏《前端面试必备》 🍚 蓝桥云课签约作者、已在蓝桥云…...

2017年五一杯数学建模A题公交车排班问题解题全过程文档及程序
2017年五一杯数学建模 A题 公交车排班问题 原题再现 随着徐州市经济的快速发展,公交车系统对于人们的出行扮演着越来越重要的角色。在公交车资源有限的情况下,合理的编排公交车的行车计划成为公交公司亟待解决的问题。以下给出公交车排班问题中的部分名…...
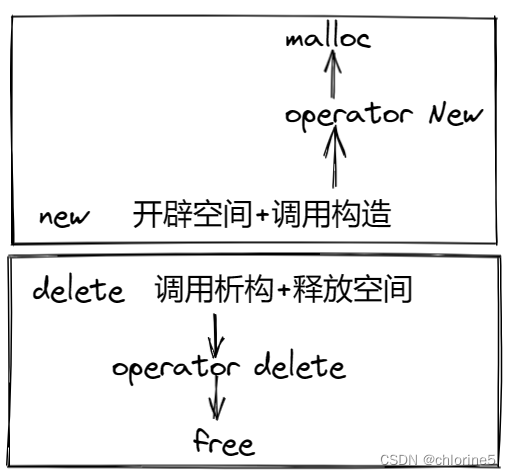
【c++】——类和对象(下) ——内存管理
作者:chlorine 专栏:c专栏 目录 💻 C/C内存分布 💻C语言中动态内存管理方式:malloc/calloc/realloc/free 编辑 💻C内存管理方式 👉new/delete操作内置类型 👉new和delete操作自定义类型 …...
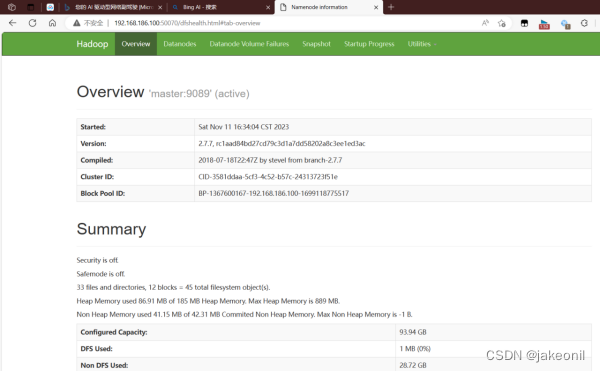
大数据平台/大数据技术与原理-实验报告--部署全分布模式Hadoop集群
实验名称 部署全分布模式Hadoop集群 实验性质 (必修、选修) 必修 实验类型(验证、设计、创新、综合) 综合 实验课时 2 实验日期 2023.10.16-2023.10.20 实验仪器设备以及实验软硬件要求 专业实验室(配有cen…...

Android Gradle 升级到7.x及Maven推送问题
7.0以下的Android插件工程使用Maven上传时脚本如下所示。 plugins {id com.android.libraryid kotlin-androidid maven }// 源代码一起打包 task androidSourcesJar(type: Jar) {archiveClassifier.set(sources)from android.sourceSets.main.java.sourceFiles }uploadArchive…...
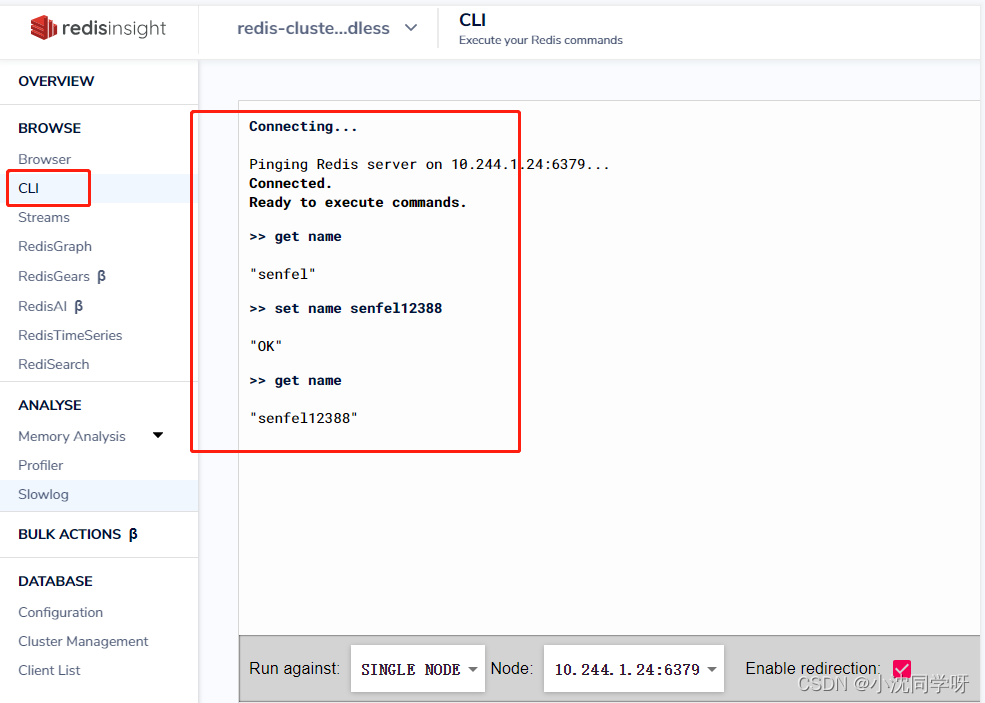
【实战】K8S Helm部署Redis Cluster Redisinsight
文章目录 前言部署Redis Cluster安装Redis Insight写在最后 前言 在Web服务的开发过程中,Redis一直以来都有着举足轻重的作用。基本上所有的后端服务都会用这个中间件实现具体的业务场景,比如常作为系统缓存、分布式锁,也可以实现排名、定位…...

3.前端--HTML标签-文本图像链接【2023.11.25】
1.HTML常用标签(文本图像链接) 文本标签 标题 <h1> - <h6> 段落<p> 我是一个段落标签 </p> 换行 <br /> <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta ht…...
ctfshow刷题web入门--1--ljcsd
文章目录 ctf.show。信息搜集web1web2web3web4web5web6web7web8web9web10web11web12web13web14web15web16web17web18web19web20。爆破。知识1.1 播种随机数生成器-mt_srand。参考web21--重点web22--做不出来web23web24web25web26web27web28。。。命令执行。知识1 绕过正则表达式…...
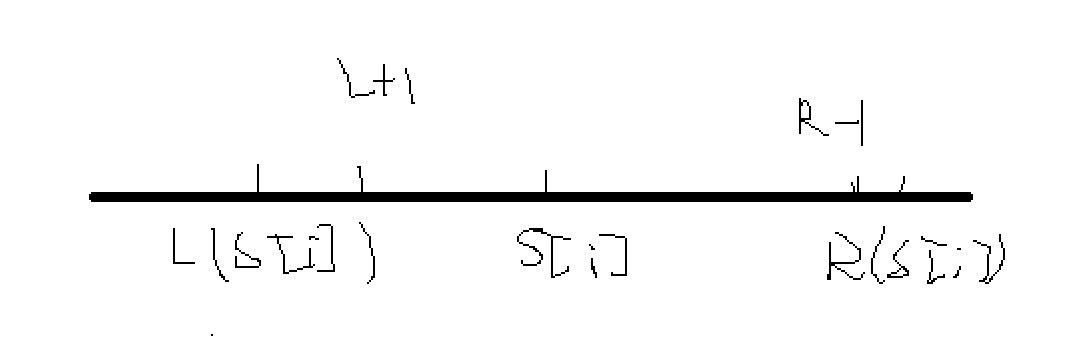
乘法原理 LeetCode 828. 统计子串中的唯一字符
我们定义了一个函数 countUniqueChars(s) 来统计字符串 s 中的唯一字符,并返回唯一字符的个数。 例如:s "LEETCODE" ,则其中 "L", "T","C","O","D" 都是唯一字符,…...
python桌面开发PyQt6库和工具库QTDesigner安装和配置
一、安装PyQt6 二、安装pyqt6-tools 三、安装外部工具 四、创建QTDesigner 1.首先查找designer.exe的路径(可以自己在窗口中选择,也可以使用Everything搜索) 2.使用Everything搜索后会出现多个designer.exe,选中,OpenPath 3.选择…...

火柴棒等式
枚举 只要在保证等式正确的基础上判断火柴棒有没有用完就可以 因为数比较小,而且我不知道最大的等式中的数是多少,索性就设置为999了 还好对效率要求不大(doge) 要不然就得自己慢慢改最大数来试了 代码如下: #in…...

给定两个字符串 s 和 t ,找不同
题意: 给定两个字符串 s 和 t ,它们只包含小写字母。 字符串 t 由字符串 s 随机重排,然后在随机位置添加一个字母。 请找出在 t 中被添加的字母。 示例 1: 输入:s “abcd”, t “abcde” 输出:“e”…...

从权限跳转看Activity的data android:scheme
在应用申请悬浮窗权限的时候,可以跳转到相应的设置界面,并且自动切换到应用的条目,高亮显示一下, android悬浮窗权限怎么申请 在Android中,要申请悬浮窗权限,需要以下步骤: 在 AndroidManifes…...

C++ Qt QFile用法介绍与代码演示
作者:令狐掌门 技术交流QQ群:675120140 csdn博客:https://mingshiqiang.blog.csdn.net/ 文章目录 打开和关闭文件读取文件写入文件示例代码自定义格式文件解析在Qt 中 QFile 的类用于读写本地文件系统中的文件。它继承自 QIODevice,所以它包含了许多用于数据输入和输出的功…...

Redis面试题:Redis的数据过期策略有哪些?
目录 面试官:Redis的数据过期策略有哪些 ? 惰性删除 定期删除 面试官:Redis的数据过期策略有哪些 ? 候选人: 嗯~,在redis中提供了两种数据过期删除策略 第一种是惰性删除,在设置该key过期时间后,我们…...

1.2.1 C语言结构体初始化方法总结
文章目录 结构体定义通用定义注册事项结构体初始化方法一简述示例方法二简述示例方法三简述示例方法四简述示例方法五简述示例结构体定义 通用定义 常用的结构体定义,有2种形式, 一种是关键字struct 结构体形式,如下...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
