数据结构-树-二叉树-堆的实现
1.树概念及结构
树是一种 非线性 的数据结构,它是由 n ( n>=0 )个有限结点组成一个具有层次关系的集合。 把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的 。
- 有一个特殊的结点,称为根结点,根节点没有前驱结点
- 除根节点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1<= i
- <= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继
- 因此,树是递归定义的。
注意:树形结构中,子树之间不能有交集,否则就不是树形结构
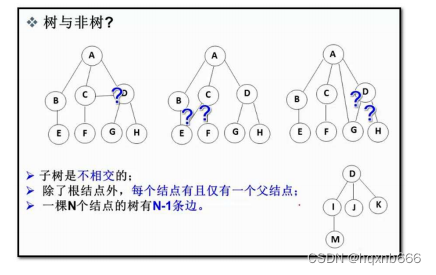
1.2 树的相关概念
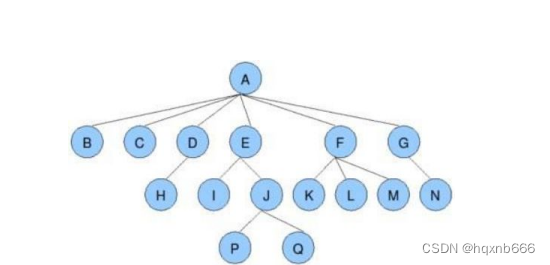
- 节点的度:一个节点含有的子树的个数称为该节点的度;如上图:A的为6
- 叶节点或终端节点:度为0的节点称为叶节点;如上图:B、C、H、I...等节点为叶节点
- 非终端节点或分支节点:度不为0的节点;如上图:D、E、F、G...等节点为分支节点
- 双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点;如上图:A是B的父节点
- 孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点;如上图:B是A的孩子节点
- 兄弟节点:具有相同父节点的节点互称为兄弟节点;如上图:B、C是兄弟节点
- 树的度:一棵树中,最大的节点的度称为树的度;如上图:树的度为6
- 节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
- 树的高度或深度:树中节点的最大层次;如上图:树的高度为4
- 堂兄弟节点:双亲在同一层的节点互为堂兄弟;如上图:H、I互为兄弟节点
- 节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先
- 子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙
- 森林:由m(m>0)棵互不相交的树的集合称为森林;
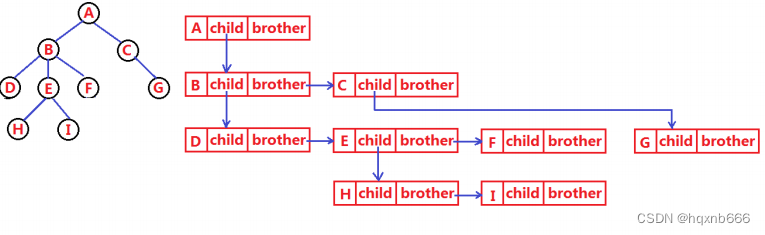
1.3 树的表示
树结构相对线性表就比较复杂了,要存储表示起来就比较麻烦了,既然保存值域,也要保存结点和结点之间
typedefintDataType;structNode
{
structNode*_firstChild1; // 第一个孩子结点
structNode*_pNextBrother; // 指向其下一个兄弟结点
DataType_data; // 结点中的数据域
};
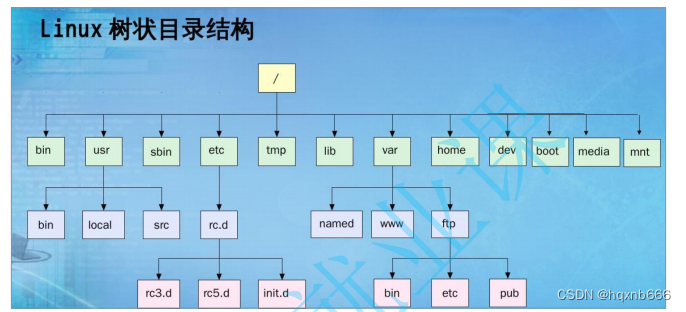
1.4 树在实际中的运用(表示文件系统的目录树结构)
2.二叉树概念及结构
2.1概念
一棵二叉树是结点的一个有限集合,该集合
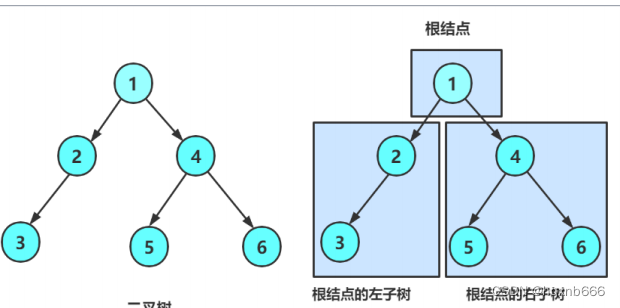
从上图可以看出:
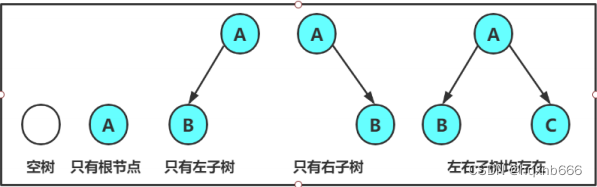
2.2 特殊的二叉树
1. 满二叉树 :一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为 K ,且结点总数是,则它就是满二叉树。2. 完全二叉树 :完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为 K的,有 n 个结点的二叉树,当且仅当其每一个结点都与深度为 K 的满二叉树中编号从 1 至 n 的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。
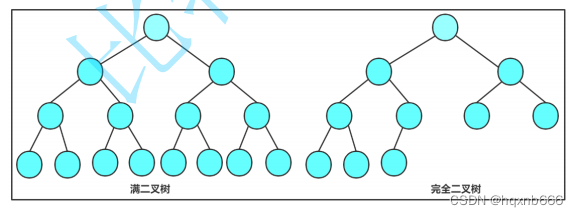
2.3 二叉树的性质
1. 若规定根节点的层数为 1 ,则一棵非空二叉树的 第 i 层上最多有2^i-1个结点 .2. 若规定根节点的层数为 1 ,则 深度为 h 的二叉树的最大结点数是2^h -1.3. 对任何一棵二叉树 , 如果度为 0 其叶结点个数为n0 , 度为 2 的分支结点个数为 n2 , 则有 n0=n2 + 14. 若规定根节点的层数为 1 ,具有 n 个结点的满二叉树的深度 , h=log2 ^(n+1). (ps :是 log 以 2为底, n+1 为对数 )5. 对于具有 n 个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从 0 开始编号,则对于序号为 i的结点有:1. 若 i>0 , i 位置节点的双亲序号: (i-1)/2 ; i=0 , i 为根节点编号,无双亲节点2. 若 2i+1<n ,左孩子序号: 2i+1 , 2i+1>=n 否则无左孩子3. 若 2i+2<n ,右孩子序号: 2i+2 , 2i+2>=n 否则无右孩子
2.4 二叉树的存储结构
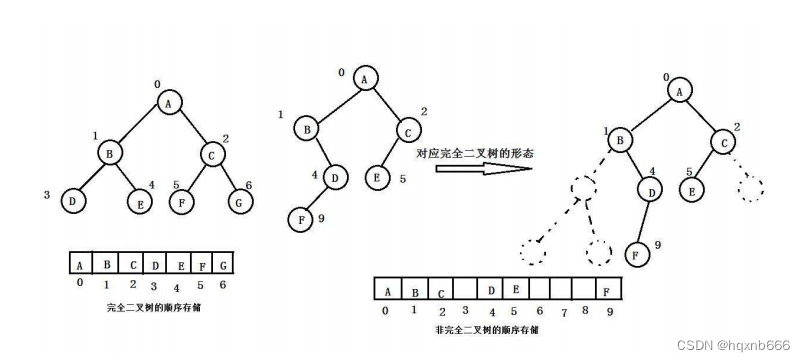
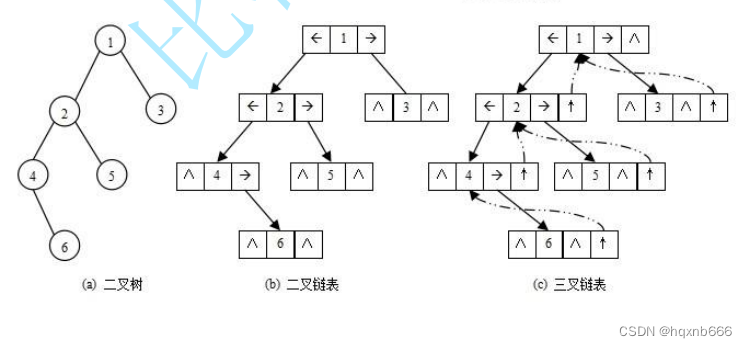
3.二叉树的顺序结构及实现
3.1 二叉树的顺序结构
普通的二叉树是不适合用数组来存储的,因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结 构存储。现实中我们通常把堆 ( 一种二叉树 ) 使用顺序结构的数组来存储,需要注意的是这里的堆和操作系统虚拟进程地址空间中的堆是两回事,一个是数据结构,一个是操作系统中管理内存的一块区域分段。
3.2 堆的概念及结构
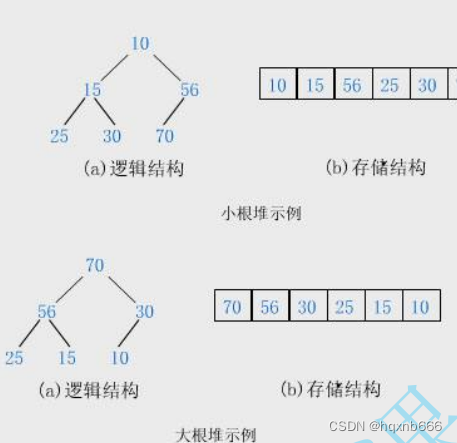
4. 堆的实现
4.1 堆向下调整算法

4.2堆的创建

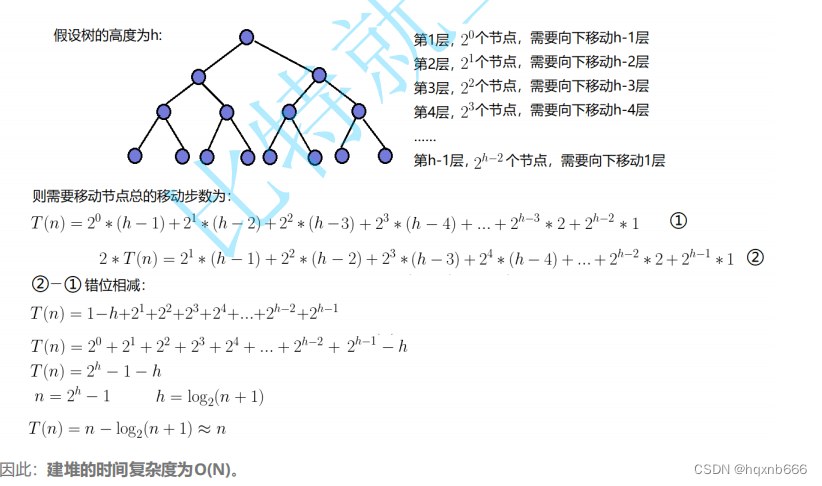
4.3 建堆时间复杂度
 4.4 堆的插入
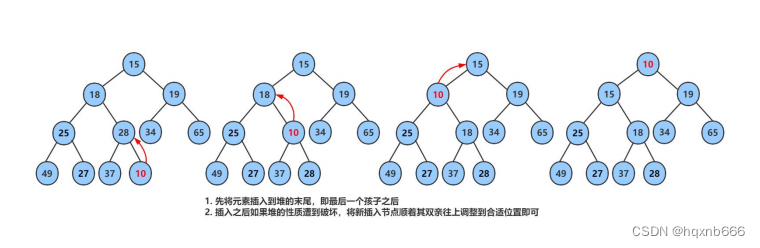
4.4 堆的插入
先插入一个10到数组的尾上,再进行向上调整算法,直到满足堆。
4.5 堆的删除
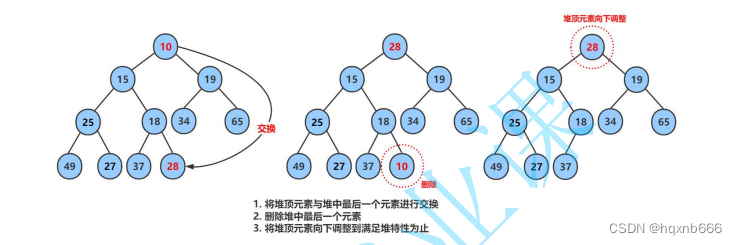
typedef int HPDataType;
typedef struct Heap
{HPDataType* _a;int _size;int _capacity;
}Heap;
// 堆的构建
void HeapCreate(Heap* hp, HPDataType* a, int n);
// 堆的销毁
void HeapDestory(Heap* hp);
// 堆的插入
void HeapPush(Heap* hp, HPDataType x);
// 堆的删除
void HeapPop(Heap* hp);
// 取堆顶的数据
HPDataType HeapTop(Heap* hp);
// 堆的数据个数
int HeapSize(Heap* hp);
// 堆的判空
int HeapEmpty(Heap* hp);通过以上的代码详解,我们了解了基于数组实现的二叉树-堆的基本操作,包括初始化、销毁、入堆、出堆等操作,并深入探讨了如何通过上浮和下沉操作来维护堆的性质。这些操作使得堆成为一种高效的数据结构,特别适用于需要频繁获取最大或最小元素的场景。希望通过这篇博客,读者能够更加深入地理解二叉树-堆的实现原理。
相关文章:

数据结构-树-二叉树-堆的实现
1.树概念及结构 树是一种 非线性 的数据结构,它是由 n ( n>0 )个有限结点组成一个具有层次关系的集合。 把它叫做树是因 为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的 。 有一个特殊的结点ÿ…...
两巨头Facebook 和 GitHub 联手推出 Atom-IDE
9月13日,GitHub 宣布与 Facebook 合作推出了 Atom-IDE —— 它包括一系列将类 IDE 功能带到 Atom 的可选工具包。初次发布的版本包括更智能、感知上下文的自动完成;导航功能,如大纲视图和定义跳转(outline view and goto-definition)…...

python生成邀请码,手机验证码
python生成邀请码,手机验证码 使用python生成邀请码,手机验证码,大小写字母,数字等,示例代码如下。 1、获取随机码 import randomdef get_random_code(is_digit=False, num=6):获取随机码:param is_digit: 是否为全数字:param num: 长度:return:if is_digit:sequence =…...

分布式链路追踪入门篇-基础原理与快速应用
为什么需要链路追踪? 我们程序员在日常工作中,最常做事情之一就是修bug了。如果程序只是运行在单机上,我们最常用的方式就是在程序上打日志,然后程序运行的过程中将日志输出到文件上,然后我们根据日志去推断程序是哪一…...
新的centos7.9安装jenkins—(一)
更多ruoyi-nbcio功能请看演示系统 gitee源代码地址 前后端代码: https://gitee.com/nbacheng/ruoyi-nbcio 演示地址:RuoYi-Nbcio后台管理系统 因为是用java8,所以还是要最后java8版本的jenkins,版本号是2.346.3,后…...

Go语言初始化已有环境,跟踪已有依赖环境
在Go语言中,go.mod文件是Go模块的管理文件,用于跟踪和管理项目的依赖关系。go.sum 文件是 Go 语言模块的另一个关键文件,它记录了项目依赖的确切版本以及相应的哈希值。如果你得到了一个包含go.mod和go.sum文件的Go代码,ÿ…...

短视频获客系统成功分享,与其开发流程与涉及到的技术
先来看实操成果,↑↑需要的同学可看我名字↖↖↖↖↖,或评论888无偿分享 一、短视频获客系统的开发流程 1. 需求分析:首先需要对目标用户进行深入了解,明确系统的功能和目标,制定详细的需求文档。 2. 系统设计&#…...
antv/g6的学习总结
新建一个简单实例 1、使用命令行在项目目录下执行以下命令 cnpm install --save antv/g6 2、创建容器 <div id"mountNode"></div> 3、在需要用的 G6 的 JS 文件中导入 import G6 from antv/g6; 4、 数据准备 引入 G6 的数据源为 JSON 格式的对象。…...
带你用uniapp从零开发一个仿小米商场_6. 配置uniapp项目底部导航栏tabbar
uniapp底部tabbar介绍 在uni-app中,底部tabbar是一种常见的导航方式,它可以让用户在应用的不同页面之间进行切换。通过tabBar配置项,开发者可以指定一级导航栏和tab切换时显示的对应页。 在底部tabbar中,每个tab都有一个页面路径…...

curl添加https服务
CURL支持的通信协议有FTP、FTPS、HTTP、HTTPS、TFTP、SFTP、Gopher、SCP、Telnet、DICT、FILE、LDAP、LDAPS、IMAP、POP3、SMTP和RTSP。 首选删除系统自带的openssl,因为他只有可执行程序和库,没有头文件。 sudo apt-get remove openssl openssl官网&am…...
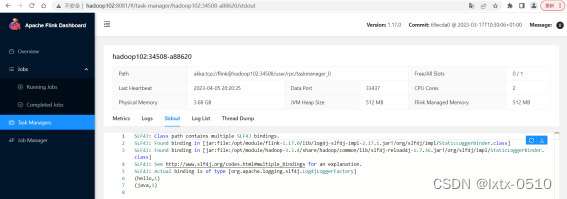
【Flink】Standalone运行模式
独立模式是独立运行的,不依赖任何外部的资源管理平台;当然独立也是有代价的:如果资源不足,或者出现故障,没有自动扩展或重分配资源的保证,必须手动处理。所以独立模式一般只用在开发测试或作业非常少的场景…...

Kotlin学习——流程控制,when,循环,range工具 kt里的equals if实现类似三元表达式的效果
Kotlin 是一门现代但已成熟的编程语言,旨在让开发人员更幸福快乐。 它简洁、安全、可与 Java 及其他语言互操作,并提供了多种方式在多个平台间复用代码,以实现高效编程。 https://play.kotlinlang.org/byExample/01_introduction/02_Functio…...

利用STM32CubeMX解读时钟树
1,低速时钟 LSE是外部晶振作时钟源,主要提供给实时时钟模块,所以一般采用32.768KHz。LSI是由内部RC振荡器产生,也主要提供给实时时钟模块,频率大约为40KHz。(LSE和LSI)只是提供给芯片中的RTC(实时时钟)及IWDG(独立看门…...
Unity-链接MySql8.0
链接MySql8.0 1.准备dll 一、找到l18N相关的dll 这里给出一个参考地址 D:\Unity\2020.3.48f1c1\Editor\Data\MonoBleedingEdge\lib\mono\unityjit在里面找到如下图的四个dll 二、下载数据库链接dll https://downloads.mysql.com/archives/c-net/在这里搜索历史版本(Archiv…...

Hive csv文件导入Hive
一、如何把csv文件导入Hive (1) 在Hive中建立与csv相对应的表 create table if not exists tmp.tmp_wenxin_20231123 (redeem_code_id string comment ) ROW FORMAT DELIMITED FIELDS TERMINATED BY , STORED AS TEXTFILE;创建了一张名为tmp_wenxin_20231123的hive表&am…...
嵌入式的学习需要合理规划时间
低级的欲望放纵即可获得,高级的欲望只有克制才能达成。——卡耐基1、粉丝的误会 很多粉丝,问我, "胡老师我想报您的培训班。" ... 得知我知识业余时间写文章,紧接着又会问, "jg单位这么清闲啊&#…...
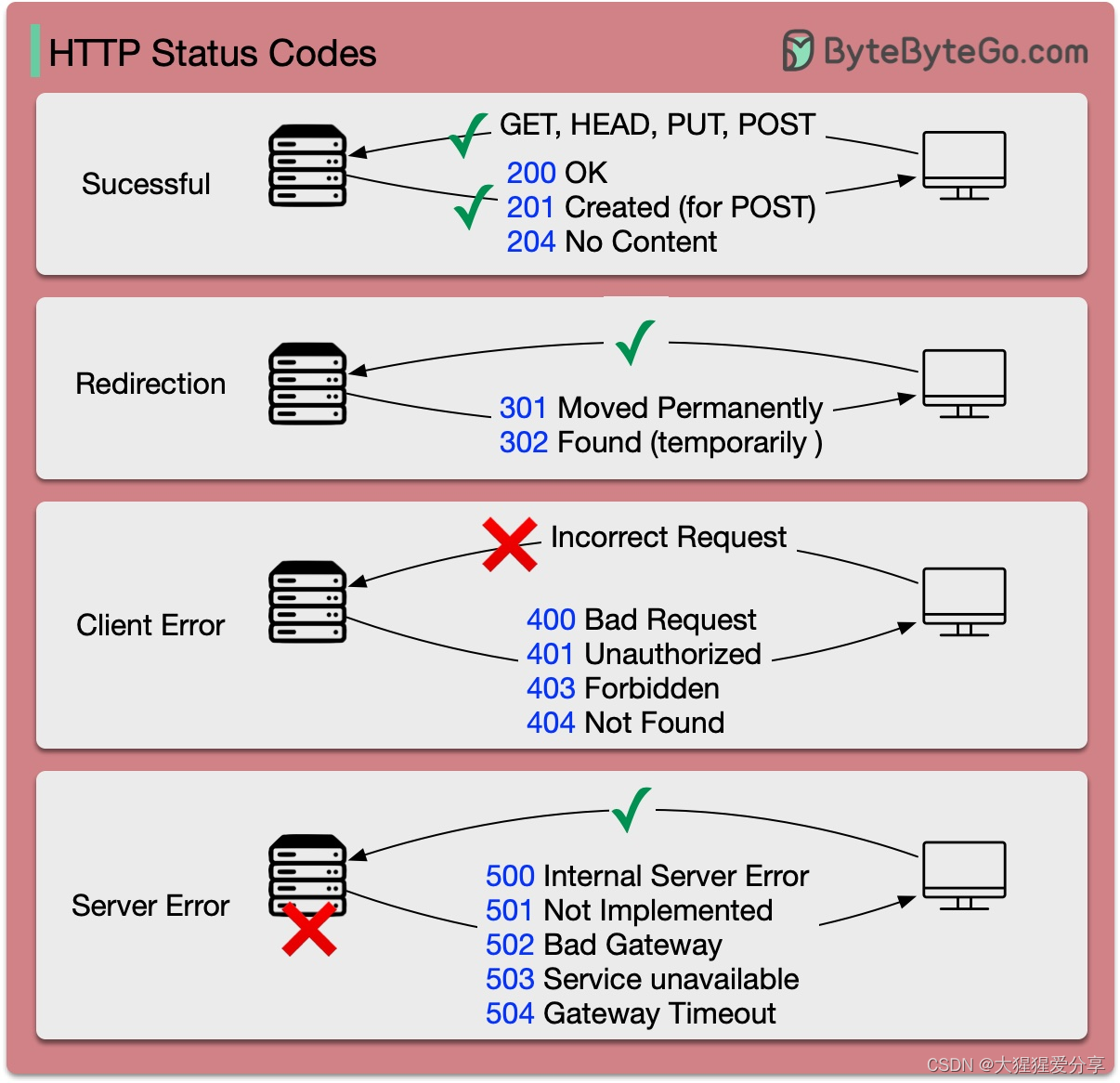
HTTP协议发展
HTTP 1.0 -> HTTP 1.1 -> HTTP 2.0 -> HTTP 3.0 (QUIC) 每一代HTTP解决了什么问题? 下图说明了主要功能。 HTTP 1.0 于 1996 年最终确定并完整记录。对同一服务器的每个请求都需要单独的 TCP 连接。 HTTP 1.1 于 1997 年发布。TCP 连接可以保持打开状态…...

杰发科技AC7801——ADC软件触发的简单使用
前言 7801资料读起来不是很好理解,大概率是之前MTK的大佬写的。在此以简单的方式进行描述。我们做一个简单的规则组软件触发Demo。因为规则组通道只有一个数据寄存器,因此还需要用上DMA方式搬运数据到内存。 AC7801的ADC简介 7801的ADC是一种 12 位 逐…...

佳易王个体诊所门诊电子处方软件试用版下载,佳易王电子处方软件的配方模板功能作用与教程
佳易王个体诊所门诊电子处方软件试用版下载,佳易王电子处方软件的配方模板功能作用与教程 1、软件试用版及教程可以点击下方的官网卡片 2、软件中有一个实用的功能,配方模板功能,在开处方单时候可以一键导入配方,节省时间。 而…...

FFmpeg零基础学习(二)——视频文件信息获取
目录 前言正文一、获取宽高信息1、核心代码2、AVFormatContext3、avformat_alloc_context4、avformat_open_input5、avformat_find_stream_info6、av_dump_format7、av_find_best_stream End、遇到的问题1、Qt Debug模式avformat_alloc_context 无法分配对象,而Rele…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

水泥厂自动化升级利器:Devicenet转Modbus rtu协议转换网关
在水泥厂的生产流程中,工业自动化网关起着至关重要的作用,尤其是JH-DVN-RTU疆鸿智能Devicenet转Modbus rtu协议转换网关,为水泥厂实现高效生产与精准控制提供了有力支持。 水泥厂设备众多,其中不少设备采用Devicenet协议。Devicen…...

Android写一个捕获全局异常的工具类
项目开发和实际运行过程中难免会遇到异常发生,系统提供了一个可以捕获全局异常的工具Uncaughtexceptionhandler,它是Thread的子类(就是package java.lang;里线程的Thread)。本文将利用它将设备信息、报错信息以及错误的发生时间都…...

如何在Windows本机安装Python并确保与Python.NET兼容
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

TJCTF 2025
还以为是天津的。这个比较容易,虽然绕了点弯,可还是把CP AK了,不过我会的别人也会,还是没啥名次。记录一下吧。 Crypto bacon-bits with open(flag.txt) as f: flag f.read().strip() with open(text.txt) as t: text t.read…...

js 设置3秒后执行
如何在JavaScript中延迟3秒执行操作 在JavaScript中,要设置一个操作在指定延迟后(例如3秒)执行,可以使用 setTimeout 函数。setTimeout 是JavaScript的核心计时器方法,它接受两个参数: 要执行的函数&…...
