算法基础一
两数之和
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。
解题思路:这道题最优的做法时间复杂度是O(n),顺序扫描数组,对每一个元素在map中找能组合给定值的另一半数字,如果找到了直接返回2个数字的下标。如果找不到就把数字放入map,进入下一次循环。
class Solution {public int[] twoSum(int[] nums, int target) {if (nums == null) {return null;}if (nums.length <= 1) {return null;}Map<Integer, Integer> map = new HashMap<>();for (int i = 0; i < nums.length; i++) {int res = target - nums[i];if (map.get(res) != null) {return new int[]{map.get(res), i};}map.put(nums[i], i);}return null;}}
两数相加
给你两个 非空 的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储 一位数字。请你将两个数相加,并以相同形式返回一个表示和的链表。
解题思路:为了处理方法统一,可以先建立一个虚拟头节点,这个虚拟头结点的next指向真正的head,这样head不需要单独处理,直接while循环即可。另外判断循环终止的条件不是p.next !=null ,这样最后一位还需要额外计算,循环条件应该是p != null。
public ListNode addTwoNumbers(ListNode l1, ListNode l2) {if (l1 == null || l2 == null) {return null;}// 进位的数,要么0要么1int carry = 0;ListNode res = new ListNode();ListNode pre = res;while(l1 != null ||l2 != null) {int v1 = l1 == null ? 0 : l1.val;int v2 = l2 == null ? 0 : l2.val;// 求和int sum = v1 + v2 + carry;// 计算进位carry = sum / 10;// 求和排除大于10的情况sum = sum % 10;res.next = new ListNode(sum);res = res.next;if (l1 != null) {l1 = l1.next;}if (l2 != null) {l2 = l2.next;}}if (carry == 1) {// 进位了res.next = new ListNode(carry);}return pre.next;}
无重复字符的最长子串
给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。
示例 1:
输入: s = "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
示例 2:
输入: s = "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b",所以其长度为 1。
示例 3:
输入: s = "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke",所以其长度为 3。
请注意,你的答案必须是 子串 的长度,"pwke" 是一个子序列,不是子串。
解题思路: 思想是滑动窗口,滑动窗口的右边界不断地右移,只要没有重复的字符,就持续向右扩大窗口边界。一旦出现重复字符,就需要缩小左边界,然后继续移动滑动窗口的右边界。以此类推,每次移动需要计算当前长度,并判断是否需要更新最大长度。
public int lengthOfLongestSubstring(String s) {int len = s.length();Set<Character> temp = new HashSet<Character>();int rk = -1;int res = 0;for(int i = 0; i < len; ++i) {if (i != 0) {// 从第二个开始,移除前一个temp.remove(s.charAt(i - 1));}while(rk + 1 < len && !temp.contains(s.charAt(rk + 1))) {// 持续向右移动temp.add(s.charAt(rk + 1));++rk;}res = Math.max(res, rk - i + 1);}return res;}求两个正序数组的中位数
给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的中位数 。算法的时间复杂度应该为 O(log (m+n)) 。
示例 1:
输入:nums1 = [1,3], nums2 = [2]
输出:2.00000
解释:合并数组 = [1,2,3] ,中位数 2示例 2:
输入:nums1 = [1,2], nums2 = [3,4]
输出:2.50000
解释:合并数组 = [1,2,3,4] ,中位数 (2 + 3) / 2 = 2.5
解题思路:
- 给出两个有序数组,要求找出这两个数组合并以后的有序数组中的中位数。要求时间复杂度为 O(log (m+n))
- 最容易想到的就是把两个数组合并,然后取出中位数。但是合并数组的复杂度是O(max(m+n)),所以可以考虑使用二分搜索
- 由于要找到最终合并以后数组的中位数,两个数组的总⼤⼩也知道,所以中间这个位置也是知道的。只需要⼆分搜索⼀个数组中切分的位置,另⼀个数组中切分的位置也能得到。为了使得时间复 杂度最⼩,所以⼆分搜索两个数组中⻓度较⼩的那个数组
- 关键的问题是如何切分两个数组。其实就是如何切分数组 1 。先随便⼆分产⽣⼀个 midA,切分的线何时算满⾜了中位数的条件呢?即,线左边的数都⼩于右边的数,即, nums1[midA-1] ≤ nums2[midB] && nums2[midB-1] ≤ nums1[midA] 。如果这些条件都不满 ⾜,切分线就需要调整。如果 nums1[midA] < nums2[midB-1] ,说明 midA 这条线划分出来左 边的数⼩了,切分线应该右移;如果 nums1[midA-1] > nums2[midB] ,说明 midA 这条线划分 出来左边的数⼤了,切分线应该左移。经过多次调整以后,切分线总能找到满⾜条件的解
- 假设现在找到了切分的两条线了, 数组 1 在切分线两边的下标分别是 midA - 1 和 midA 。 数 组 2在切分线两边的下标分别是 midB - 1 和 midB 。最终合并成最终数组,如果数组⻓度是奇 数,那么中位数就是 max(nums1[midA-1], nums2[midB-1]) 。如果数组⻓度是偶数,那么中间 位置的两个数依次是: max(nums1[midA-1], nums2[midB-1]) 和 min(nums1[midA], nums2[midB]) ,那么中位数就是 (max(nums1[midA-1], nums2[midB-1]) + min(nums1[midA], nums2[midB])) / 2 。
public double findMedianSortedArrays(int[] nums1, int[] nums2) {int m = nums1.length;int n = nums2.length;int len = m + n;int left = -1;int right = -1;int aStart = 0;int bStart = 0;for(int i = 0; i <= len / 2; i++) {left = right;if (aStart < m && (bStart >= n || nums1[aStart] < nums2[bStart])) {right = nums1[aStart++];} else {right = nums2[bStart++];}}if ((len & 1 ) == 0) {return (left + right) / 2.0;} else {return right;}}
整数反转
给你一个 32 位的有符号整数 x ,返回将 x 中的数字部分反转后的结果。如果反转后整数超过 32 位的有符号整数的范围 [−231, 231 − 1] ,就返回 0。
假设环境不允许存储 64 位整数(有符号或无符号)。
解题思路:只需要注意一点,反转以后的数字要求在 [−2^31, 2^31 − 1] 范围内,超过这个范围的数字都要输出0。
public int reverse(int x) {int res = 0;while(x != 0) {//每次取末尾数字int tmp = x % 10;//判断是否 大于 最大32位整数if (res > 214748364 || (res == 214748364 && tmp > 7)) {return 0;}//判断是否 小于 最小32位整数if (res < -214748364 || (res == -214748364 && tmp < -8)) {return 0;}res = res * 10 + tmp;x /= 10;}return res;}
相关文章:

算法基础一
两数之和 给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。 解题思路:这道题最优的做法时间复杂度是O(n),顺序扫描数组,对每一个元素在…...
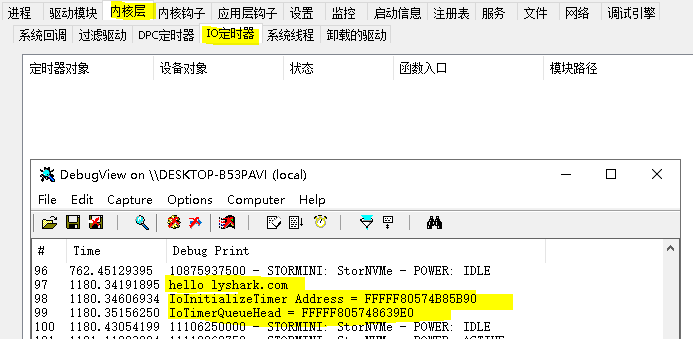
6.3 Windows驱动开发:内核枚举IoTimer定时器
内核I/O定时器(Kernel I/O Timer)是Windows内核中的一个对象,它允许内核或驱动程序设置一个定时器,以便在指定的时间间隔内调用一个回调函数。通常,内核I/O定时器用于周期性地执行某个任务,例如检查驱动程序…...
)
大数据-之LibrA数据库系统告警处理(ALM-37005 GTM进程异常)
告警解释 当出现如下情况时,产生该告警: GTM实例数据目录中的gtm.conf配置文件不存在或者其中某个配置参数不正确时。GTM实例服务线程无法监听IP,或者无法绑定监听端口。GTM实例进程没有其数据目录读写权限时。 告警属性 告警ID 告警级别…...

一种LED驱动专用控制电路
一、基本概述 TM1620是一种LED(发光二极管显示器)驱动控制专用IC,内部集成有MCU数字接口、数据锁存 器、LED驱动等电路。本产品质量可靠、稳定性好、抗干扰能力强。主要适用于家电设备(智能热 水器、微波炉、洗衣机、空调、电磁炉)、机顶盒、电子称、…...
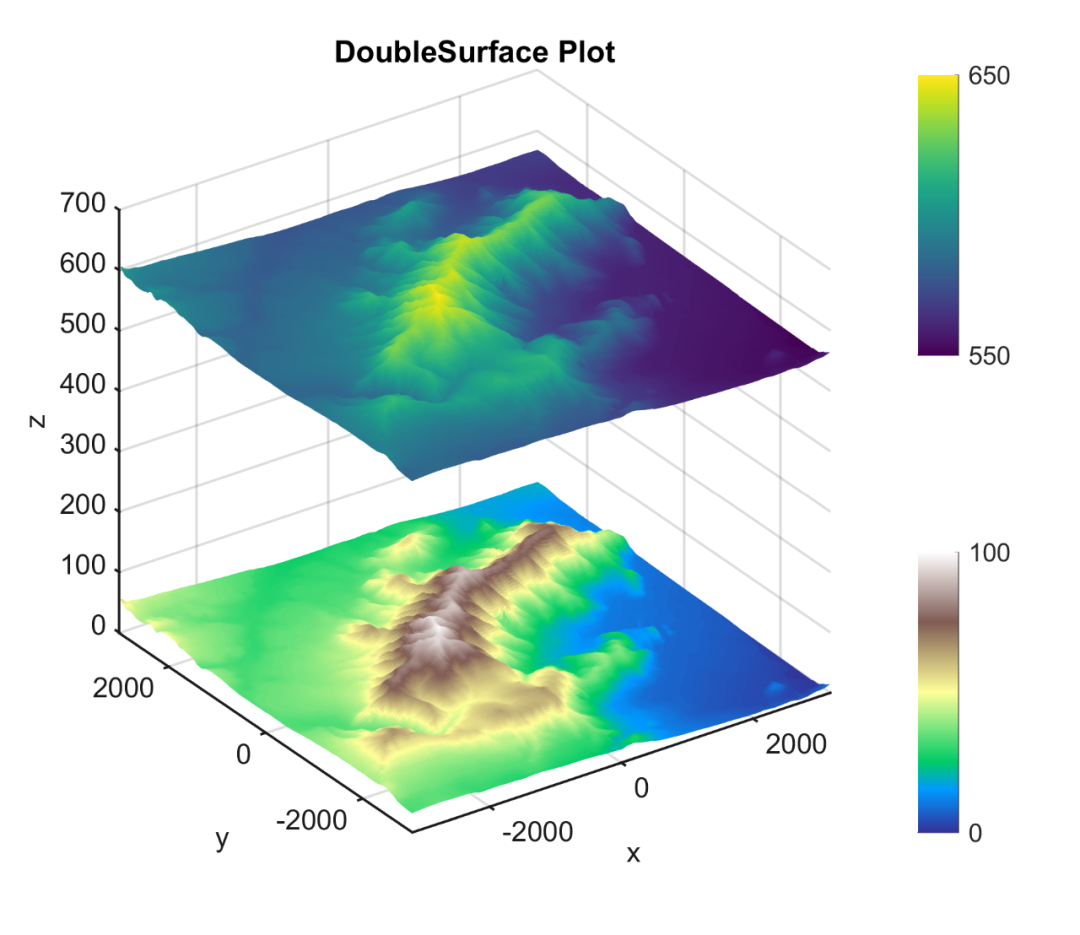
Matlab进阶绘图第33期—双曲面图
在《Matlab论文插图绘制模板第56期—曲面图(Surf)》中,我分享过曲面图的绘制模板。 然而,有的时候,需要在一张图上绘制两个及以上的曲面图,且每个曲面图使用不同的配色方案。 在Matlab中,一张…...
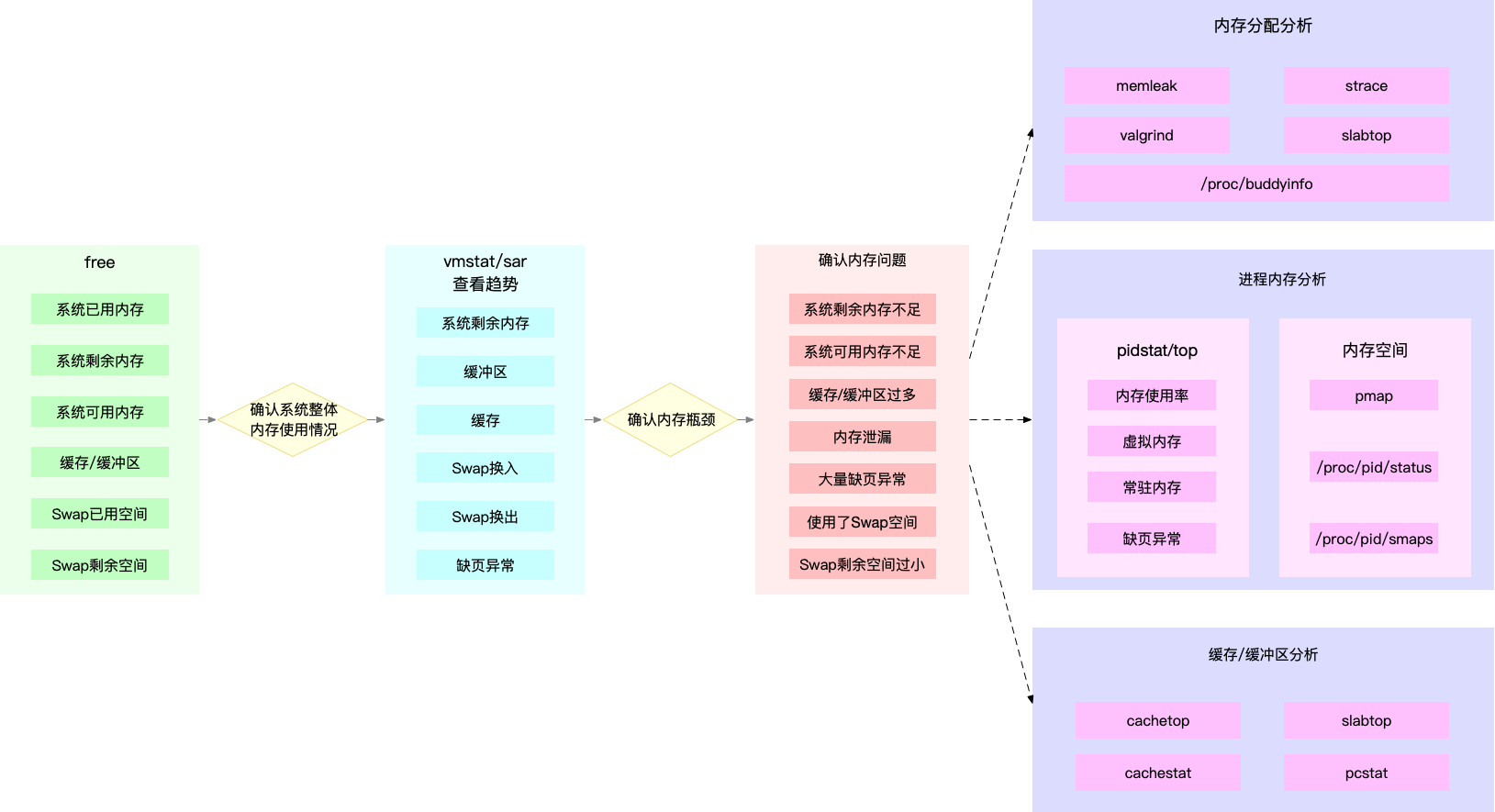
【Linux】23、内存超详细介绍
文章目录 零、资料一、内存映射1.1 TLB1.2 多级页表1.3 大页 二、虚拟内存空间分布2.1 用户空间的段2.2 内存分配和回收2.2.1 小对象2.2.2 释放 三、查看内存使用情况3.1 Buffer 和 Cache3.1.1 proc 文件系统3.1.2 案例3.1.2.1 场景 1:磁盘和文件写案例3.1.2.2 场景…...
官网IDM下载和安装的详细步骤
目录 一、IDM是什么 二、下载安装 三、解决下载超时的问题 四、谷歌浏览器打开IDM插件 谷歌浏览器下载官网👇 五、测试 六、资源包获取 一、IDM是什么 IDM(internet download manager)是一个互联网下载工具插件,常见于用…...
)
【面经八股】搜广推方向:常见面试题(三)
【面经&八股】搜广推方向:常见面试题(三) 文章目录 【面经&八股】搜广推方向:常见面试题(三)1. 如何解决数据不平衡2. 假设检验的两类错误3. 为什么快排比堆排快4. RMSE、MSE、MAE5. 双塔模型的应用6. XGBoost如果损失函数没有二阶导,该怎么办7. AUC是如何实现的…...
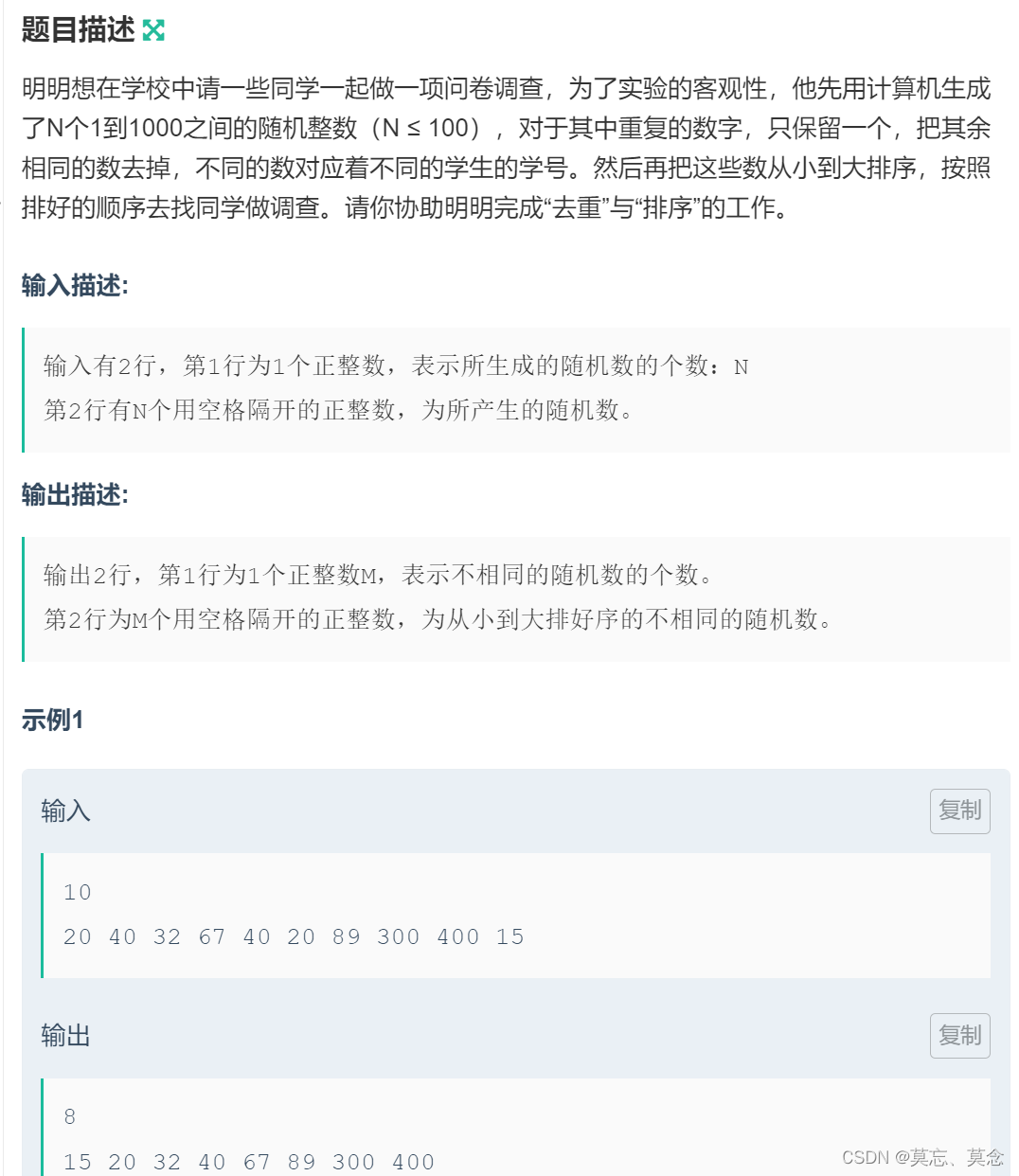
[NOIP2006]明明的随机数
一、题目 登录—专业IT笔试面试备考平台_牛客网 二、代码 set去重,再利用vector进行排序 std::set是一个自带排序功能的容器,它已经按照一定的规则(默认是元素的小于比较)对元素进行了排序。因此,你不能直接对std::s…...

auth模块
一. auth模块前戏 # 引入:其实我们在创建好一个django项目之后直接执行数据库迁移命令会自动生成很多表 例如:django_sessionauth_user我们知道django在启动之后就可以直接访问admin路由,需要输入用户名和密码,数据参考的就是auth_user表,并且还必须是管…...

H5ke12--3--iframe--编辑邮箱的制作
下面我们来window.iframes[] frames是一个全局变量,它是一个对象数组,其中包含当前窗口中的所有框架(如果存在)。 在这段代码中,let frameframes[0];是将第一个框架赋值给变量frame。通过frame.document.designMode&q…...

Python面经【3】
零、可迭代对象 可迭代对象是迭代器和生成器的基础,简单来说,可以使用for循环遍历的对象就是可迭代对象,比如常见的list、set和dict。在python中,可迭代对象是指实现了__iter__()方法的对象,当我们使用for循环遍历一个…...
Python集合类型
目录 目标 版本 官方文档 集合分类 实战 创建 循环 常用方法 目标 掌握set和frozenset两种集合的使用方法,包括:创建、交集、并集、差集等操作。 版本 Python 3.12.0 官方文档 Set Types — set, frozensethttps://docs.python.org/3/library/s…...

npm install报错常用解题思路
最近刚接手一个“新”项目,让我很无语。明明是去年起的项目,但是它所用的部分技术栈非常旧,我启动项目,控制台一堆warning报错,然后项目结构也很让我不适应,很多地方都可以用文件夹包一下来方便定位。哎&am…...

conda: error: argument COMMAND: invalid choice
简介 使用conda activate 时,可能会报:conda: error: argument COMMAND: invalid choice: ‘activate’ (choose from ‘clean’, ‘compare’, ‘config’, ‘create’, ‘info’, ‘init’, ‘install’, ‘list’, ‘notices’, ‘package’, ‘remo…...
数仓成本下降近一半,StarRocks 存算分离助力云览科技业务出海
成都云览科技有限公司倾力打造了凤凰浏览器,专注于为海外用户提供服务,公司致力于构建一个全球性的数字内容连接入口,为用户带来更为优质、高效、个性化的浏览体验。 作为数据驱动的高科技公司,从数据中挖掘价值一直是公司核心任务…...

Apache基线检查
一、确保对OS根目录禁用覆盖 当 AllowOverride 指令设置为 None 时,Apache 将禁止在该目录下使用 .htaccess 文件来覆盖任何配置项。这意味着,除非您在主配置文件中显式地指定,否则该目录下的任何 .htaccess 文件都将被忽略。 禁用 .htaccess 文件可以提高服务器的安全性,因…...

flink的集成测试
背景 日常测试中我们使用flink的TestHarness只能测试单个算子,很多情况下我们需要集成测试来测试真正的问题,所以在flink中进行集成测试还是非常有必要的,本文就来记录下如何在flink中进行集成测试 flink中进行集成测试 flink中进行集成测…...

gitee推荐-1Panel
以下内容来源于gitee。 gitee地址:1Panel: 🔥 🔥 🔥 现代化、开源的 Linux 服务器运维管理面板。 大概和宝塔类似,但支持docker。在线体验:https://demo.1panel.cn/ 稍微试了下,没找到apache,…...
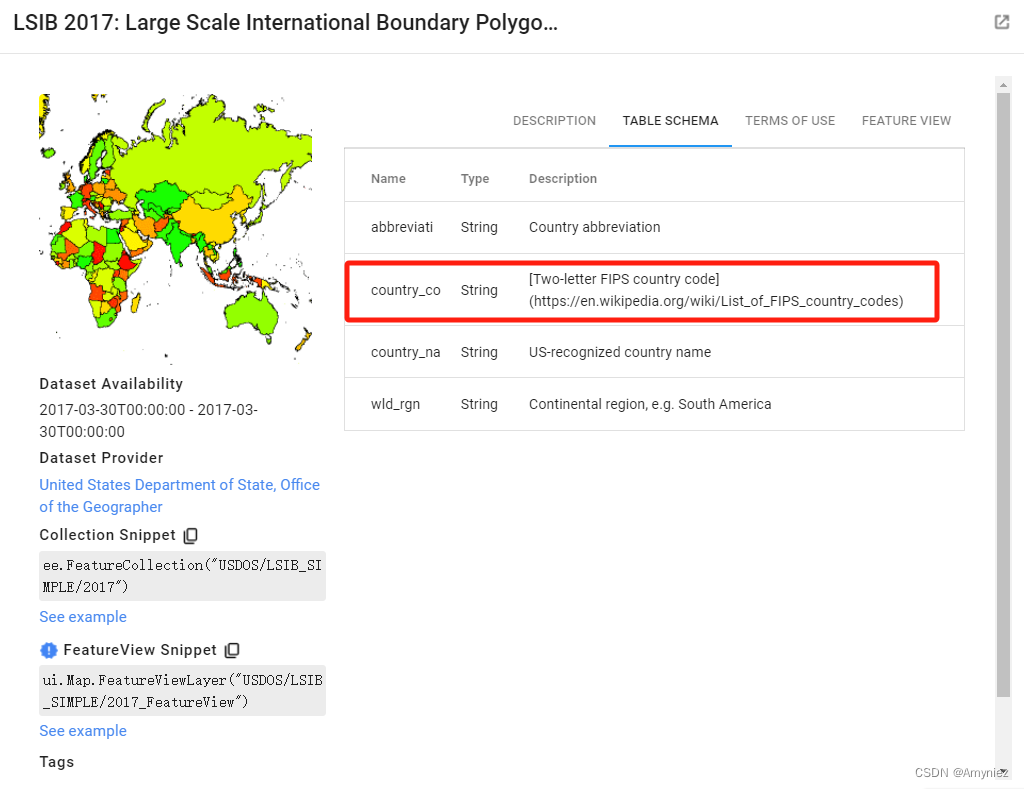
GEE 22:基于GEE实现物种分布模型(更新中。。。。。。)
物种分布模型 1. 数据点准备1.1 数据加载1.2 去除指定距离内的重复点1.3 定义研究区范围1.4 选择预测因子 1. 数据点准备 1.1 数据加载 首先需要将CSV文件导入到GEE平台中,同样也可以导入shp格式文件。 // 1.Loading and cleaning your species data *************…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...
