87-96-多维动态规划、技巧
LeetCode 热题 100
文章目录
- LeetCode 热题 100
- 多维动态规划
- 87. 中等-不同路径
- 88. 中等-最小路径和
- 89. 中等-最长回文子串
- 90. 中等-最长公共子序列
- 91. 困难-编辑距离
- 技巧
- 92. 简单-只出现一次的数字
- 93. 简单-多数元素
- 94. 中等-颜色分类
- 95. 中等-下一个排列
- 96. 中等-寻找重复数
本文存储我刷题的笔记。
多维动态规划
87. 中等-不同路径
88. 中等-最小路径和
89. 中等-最长回文子串
90. 中等-最长公共子序列
91. 困难-编辑距离
技巧
92. 简单-只出现一次的数字

我的思路:哈希表
- 思路:用哈希集合
std::unordered_set,遍历所有元素,没遇过就存起来,遇到了就删除哈希集合对应元素,最后哈希集合中剩下的元素就是。- 时间复杂度: O ( n ) O(n) O(n),其中 n n n 是数组长度。只需要对数组遍历一次。
- 空间复杂度: O ( n ) O(n) O(n),最多可能会存储 n / 2 n/2 n/2 个元素。
- 时间24ms(20.69%),内存19.81MB(8.87%)。
class Solution {
public:int singleNumber(std::vector<int>& nums) {int len = nums.size();std::unordered_set<int> s_num;for(int i=0; i<len; i++){// 遇到有的就擦除if(s_num.count(nums[i])){s_num.erase(nums[i]); }// 遇到没有的就存起来else{s_num.emplace(nums[i]);}}// 返回只剩下的最后一个元素return *s_num.begin();}
};
官方思路一:位运算
- 思路:因为只有一个数和其他的都不一样,所以将所有数字都进行异或运算,最后就只剩下那个单独的数字。
- 时间复杂度: O ( n ) O(n) O(n),其中 n n n 是数组长度。只需要对数组遍历一次。
- 空间复杂度: O ( 1 ) O(1) O(1)。
- 时间8ms(98.78%),内存16.89MB(37.16%)。
class Solution {
public:int singleNumber(vector<int>& nums) {int ret = 0;for (auto e: nums) ret ^= e;return ret;}
};
93. 简单-多数元素

我的思路:哈希表
- 思路:先统计,再遍历。
- 时间复杂度: O ( n ) O(n) O(n),其中 n n n 是数组
nums的长度。我们遍历数组nums一次,又至多遍历一次哈希表(最多包含 n − ⌊ n 2 ⌋ n - \lfloor \dfrac{n}{2} \rfloor n−⌊2n⌋ 个键值对)。因此总时间复杂度为 O ( n ) O(n) O(n)。- 空间复杂度: O ( n ) O(n) O(n)。哈希表最多包含 n − ⌊ n 2 ⌋ n - \lfloor \dfrac{n}{2} \rfloor n−⌊2n⌋ 个键值对,所以占用的空间为 O ( n ) O(n) O(n)。
- 时间20ms(45.10%),内存19.69MB(8.36%)。
注:由于题目保证会出现多数元素,所以也可以将这两个循环放在一起。
class Solution {
public:int majorityElement(std::vector<int>& nums) {// 使用哈希表统计所有信息// 哈希表:键-元素的大小、值-出现的次数std::unordered_map<int,int> m_data;for(auto num : nums){m_data[num] += 1;}// 找出符合要求的值int target = nums.size()/2;for(auto it=m_data.begin(); it!=m_data.end(); it++){if(it->second > target){return it->first;}}return -1;}
};
官方思路二:排序
- 思路:将数组
nums排序,那么下标为 ⌊ n 2 ⌋ \lfloor \dfrac{n}{2} \rfloor ⌊2n⌋ 的元素一定是“多数元素”。- 时间复杂度: O ( n log n ) O(n\log n) O(nlogn)。将数组排序的时间复杂度为 O ( n log n ) O(n\log n) O(nlogn)。
- 空间复杂度: O ( log n ) O(\log n) O(logn)。如果使用语言自带的排序算法,需要使用 O ( log n ) O(\log n) O(logn) 的栈空间。如果自己编写堆排序,则只需要使用 O ( 1 ) O(1) O(1) 的额外空间。
- 时间20ms(45.10%),内存19.66MB(10.82%)。
class Solution {
public:int majorityElement(vector<int>& nums) {sort(nums.begin(), nums.end());return nums[nums.size() / 2];}
};
官方思路三:随机化
- 思路:由于“多数元素”过半,那么随机挑选一个是“多数元素”的概率很大。于是代码逻辑为,随机生成一个下标,检查它是否是“多数元素”,如果是就返回,否则继续随机挑选。
- 时间复杂度:理论上最坏情况下的时间复杂度为 O ( ∞ ) O(\infty) O(∞),但实际上期望的时间复杂度为 O ( n ) O(n) O(n)。
- 空间复杂度: O ( 1 ) O(1) O(1)。随机方法只需要常数级别的额外空间。
- 时间16ms(75.52%),内存19.63MB(14.46%)。
class Solution {
public:int majorityElement(vector<int>& nums) {while (true) {int candidate = nums[rand() % nums.size()];int count = 0;for (int num : nums)if (num == candidate)++count;if (count > nums.size() / 2)return candidate;}return -1;}
};
官方思路四:分治
- 思路:分治算法递归求解。将数组分成左右两部分,分别求出左半部分的众数
a1以及右半部分的众数a2,随后在a1和a2中选出正确的众数。最后的的子问题都是长度为1的数组。- 时间复杂度: O ( n log n ) O(n\log n) O(nlogn)。推导见原文“方法四:分治”。
- 空间复杂度: O ( log n ) O(\log n) O(logn)。尽管分治算法没有直接分配额外的数组空间,但在递归的过程中使用了额外的栈空间。算法每次将数组从中间分成两部分,所以数组长度变为
1之前需要进行 O ( log n ) O(\log n) O(logn) 次递归,即空间复杂度为 O ( log n ) O(\log n) O(logn)。- 时间28ms(9.03%),内存19.58MB(21.58%)。
class Solution {// 统计目标值在指定范围内的次数int count_in_range(vector<int>& nums, int target, int lo, int hi) {int count = 0;for (int i = lo; i <= hi; ++i)if (nums[i] == target)++count;return count;}// 分治算法int majority_element_rec(vector<int>& nums, int lo, int hi) {// 递归最小的子问题:长度为1的数组if (lo == hi)return nums[lo];// 统计左右两部分的“多数元素”int mid = (lo + hi) / 2;int left_majority = majority_element_rec(nums, lo, mid);int right_majority = majority_element_rec(nums, mid + 1, hi);// 检查哪个符合出现次数标准if (count_in_range(nums, left_majority, lo, hi) > (hi - lo + 1) / 2)return left_majority;if (count_in_range(nums, right_majority, lo, hi) > (hi - lo + 1) / 2)return right_majority;return -1;}
public:int majorityElement(vector<int>& nums) {return majority_element_rec(nums, 0, nums.size() - 1);}
};
官方思路五:Boyer-Moore 投票算法
- 思路: 如果我们把众数记为 +1+1+1,把其他数记为 −1-1−1,将它们全部加起来,显然和大于 0,从结果本身我们可以看出众数比其他数多。于是,Boyer-Moore 算法的详细步骤:
- 维护一个候选众数
candidate和它出现的次数count。初始时candidate为任意值,count为0;- 遍历数组
nums中的所有元素,对于每个元素x,在判断x之前,如果count的值为0,我们先将x的值赋予candidate,随后我们判断x:如果
x与candidate相等,那么计数器count的值增加1;
如果x与candidate不等,那么计数器count的值减少1。
- 在遍历完成后,
candidate即为整个数组的众数。
- 时间复杂度: O ( n ) O(n) O(n)。Boyer-Moore 算法只对数组进行了一次遍历。
- 空间复杂度: O ( 1 ) O(1) O(1)。Boyer-Moore 算法只需要常数级别的额外空间。
- 时间12ms(93.37%),内存19.70MB(6.31%)。
class Solution {
public:int majorityElement(vector<int>& nums) {int candidate = -1;int count = 0;for (int num : nums) {if (num == candidate)++count;else if (--count < 0) {candidate = num;count = 1;}}return candidate;}
};
94. 中等-颜色分类
95. 中等-下一个排列
96. 中等-寻找重复数
我的思路
思路:
时间??ms(??%),内存??MB(??%)。
官方思路:
思路:
时间??ms(??%),内存??MB(??%)。
相关文章:

87-96-多维动态规划、技巧
LeetCode 热题 100 文章目录 LeetCode 热题 100多维动态规划87. 中等-不同路径88. 中等-最小路径和89. 中等-最长回文子串90. 中等-最长公共子序列91. 困难-编辑距离 技巧92. 简单-只出现一次的数字93. 简单-多数元素94. 中等-颜色分类95. 中等-下一个排列96. 中等-寻找重复数 …...

NX二次开发UF_CURVE_ask_wrap_curve_parents 函数介绍
文章作者:里海 来源网站:https://blog.csdn.net/WangPaiFeiXingYuan UF_CURVE_ask_wrap_curve_parents Defined in: uf_curve.h int UF_CURVE_ask_wrap_curve_parents(tag_t curve_tag, tag_t * defining_face, tag_t * defining_plane, tag_t * defin…...

使用 HTML、CSS 和 JavaScript 创建图像滑块
使用 HTML、CSS 和 JavaScript 创建轮播图 在本文中,我们将讨论如何使用 HTML、CSS 和 JavaScript 构建轮播图。我们将演示两种不同的创建滑块的方法,一种是基于opacity的滑块,另一种是基于transform的。 创建 HTML 我们首先从 HTML 代码开…...
ubuntu环境删除qtcreator方法
文章目录 方法1方法2方法3参考不同的安装方法,对应不同的删除方法 方法1 apt-get或者dpkg 方法2 QtCreatorUninstaller 方法3 MaintenanceTool...

软件测试基础知识
软件测试基本概念 1、软件程序文档,软件测试程序测试文档测试。 “程序”是指能够实现某种功能的指令的集合,“文档”是指软件在开发、使用和维护过程中产生的图文集合。; 2、软件的分类 按功能分:系统软件、应用软件 按技术架构分…...
 方法生成当前时间的ISO格式字符串,解决UTC时区差问题)
使用 .toISOString() 方法生成当前时间的ISO格式字符串,解决UTC时区差问题
方法分析: 日常开发中,有时我们需要向后端传递的时间值可能并非一个时间对象,而是字符串格式。 例 1:[2023-08-16T08:07:25.577Z] 但是我们通过 new Date() 之后直接使用 .toString() 方法得到的却并非这种格式。 例 2࿱…...
“BMP转PNG一键转换,批量处理图片,迈入高效图片管理新时代“
你是否曾经为了转换图片格式而烦恼?是否曾经因为一张一张地手动转换而感到无奈?现在,我们的全新工具将为你解决这些问题,开启高效图片管理新时代! 首先,我们进入首助编辑高手主页面,会看到有多种…...

解决Vue编程式导航路由跳转不显示目标路径问题
我们配置一个编程式导航的路由跳转,跳转到 /search 页面,并且携带categoryName和categoryId两个query参数。 this.$router.push({path: "/search",query: {categoryName: dataset.categoryname,categoryId: dataset.categoryid} }) 如果我们…...

Android studio 引用framework.jar
framework.jar 引用目录 N/O: out/target/common/obj/JAVA_LIBRARY/framework_interminate/classes.jarAndroid 9/10: out/soong/.intermediates/frameworks/base/framework/android_common/combined/framework.jarAndroid 11: out/soong/.intermediates/framewo…...
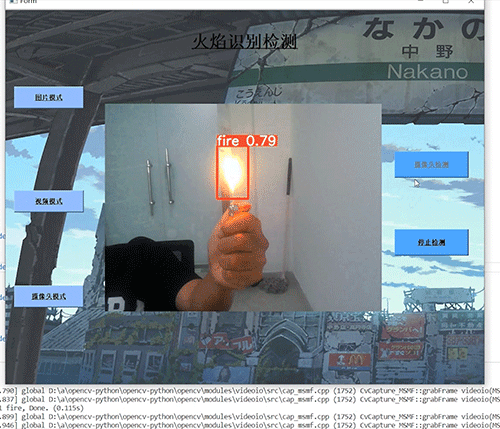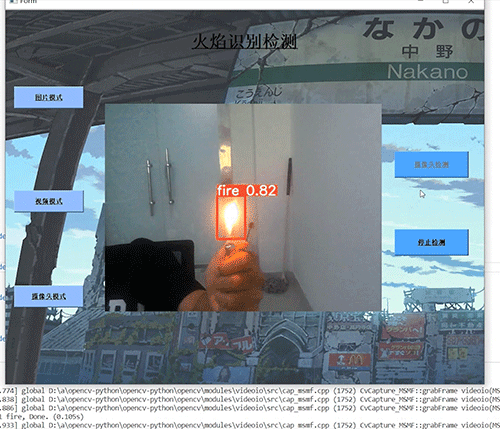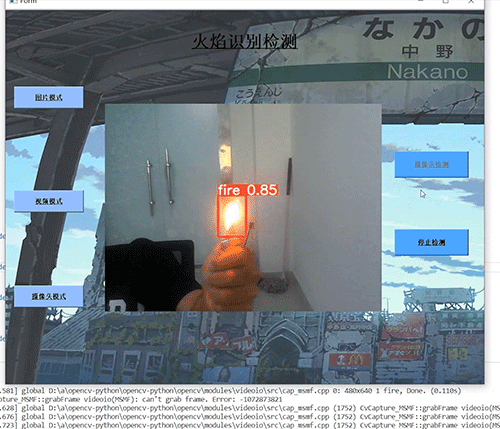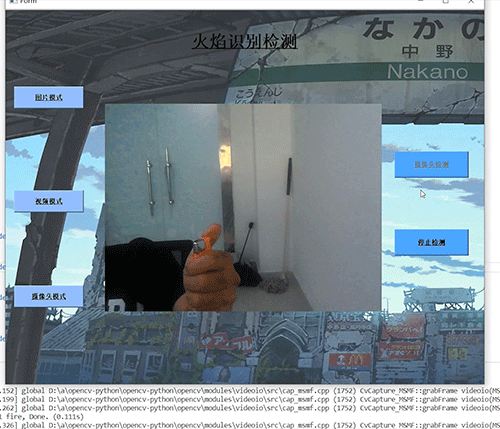
软著项目推荐 深度学习 python opencv 火焰检测识别 火灾检测
文章目录 0 前言1 基于YOLO的火焰检测与识别2 课题背景3 卷积神经网络3.1 卷积层3.2 池化层3.3 激活函数:3.4 全连接层3.5 使用tensorflow中keras模块实现卷积神经网络 4 YOLOV54.1 网络架构图4.2 输入端4.3 基准网络4.4 Neck网络4.5 Head输出层 5 数据集准备5.1 数…...

宝塔面板安装搭建DiscuzQ论坛教程与小程序上架发布后的展示效果
DiscuzQ论坛小程序上架发布后的展示效果: 1、需要用到的环境: php7.2 mysql5.7或者MariaDB 10.2(我安装用的mysql8.0) php除了必要的一些扩展外,还需要启用readlink、symlink函数等,具体看官方说明,安装的时候也会提醒…...
交换机配置与管理
文档以国产迈普交换机为例,各厂家交换机配置有少许不同,仅供参考。 交换机命令行模式: 普通用户模式Hostname>() exit 输入enable命令 特权用户模式Hostname#() exit 输入configu…...

python每日一题——7接雨水
题目 给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。 示例 1: 输入:height [0,1,0,2,1,0,1,3,2,1,2,1] 输出:6 解释:由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表…...

Ubuntu20安装ssh服务
Ubuntu20上执行如下命令查看是否存在ssh服务 #ps -e | grep ssh 只有ssh-agent,没有sshd; 因此要安装openssh-server. 搜索openssh-server,得到下载链接: openssh-server 复制这个Binary Package链接即可下载,然后使用如下命令安装 sudo…...

linux LVM /dev/sdb mount dir /data【linux LVM 磁盘挂载目录】
添加磁盘 /dev/sdb rootregistry01 ~]# fdisk -lDisk /dev/sda: 53.7 GB, 53687091200 bytes, 104857600 sectors Units sectors of 1 * 512 512 bytes Sector size (logical/physical): 512 bytes / 512 bytes I/O size (minimum/optimal): 512 bytes / 512 bytes Disk lab…...

由于找不到msvcp120.dll无法继续执行代码是什么原因怎么修复
今天我想和大家分享的是关于“msvcp120.dll丢失的解决方法”。或许有些同学在平时使用电脑的过程中会遇到这个问题,但是并不知道该如何解决。那么,接下来我将从三个方面为大家介绍:msvcp120.dll丢失的原因、msvcp120.dll是什么以及msvcp120.d…...

为你的项目加上微信登录(个人开发)
当我们开发个人项目的时候,为了用户登录的便捷性,经常会给我们的项目加上一些除了注册之外的方式,其中最常见的就是微信登录,但作为个人开发者,是无法使用微信的授权登录的,但是通过微信公众号可以获得同样…...

Pinia的使用技巧
一、安装 npm install pinia 二、main.ts引入 import { createApp } from vue import App from ./App.vue import { createPinia } from piniaconst app createApp(App) app.use(createPinia()) app.mount(#app)三、定义参数 import { defineStore } from piniatype User …...

『亚马逊云科技产品测评』活动征文|AWS 数据库产品类别及其适用场景详细说明
授权声明:本篇文章授权活动官方亚马逊云科技文章转发、改写权,包括不限于在 Developer Centre, 知乎,自媒体平台,第三方开发者媒体等亚马逊云科技官方渠道 目录 前言、AWS 数据库产品类别 01、Amazon Aurora 02、Amazon Docum…...
)
S32K324 UDS Bootloader开发-下位机篇-Bootload软件(3)
文章目录 前言校验算法34服务响应的字节字节对齐问题跳转问题Boot Delay功能重要配置跳转标志FLASH DRIVER和APP区域CAN ID配置中断使能与禁止CAN TP配置总结前言 上一篇文章介绍了S32K324 UDS Bootlodaer开发中的UDS相关的更改,本文总结一下调试过程中出现的一些问题,及解决…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...
