基本数据结构二叉树(1)
目录
1.树概念及结构
1.1树的概念
1.2 树的相关概念
1.3 树的表示
1.4 树在实际中的运用(表示文件系统的目录树结构)
2.二叉树概念及结构
2.1概念
2.2现实中的二叉树:
2.3 特殊的二叉树:
2.5 二叉树的存储结构
2. 链式存储
1.树概念及结构
1.1树的概念
树是一种 非线性 的数据结构,它是由 n ( n>=0 )个有限结点组成一个具有层次关系的集合。 把它叫做树是因 为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的 。• 有一个特殊的结点,称为根结点,根节点没有前驱结点• 除根节点外,其余结点被分成M(M>0) 个互不相交的集合 T1 、 T2 、 …… 、 Tm ,其中每一个集合 Ti(1<= i<= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有 0个或多个后继• 因此,树是递归定义的。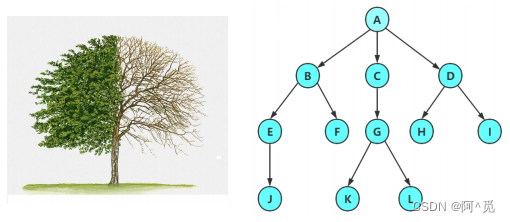
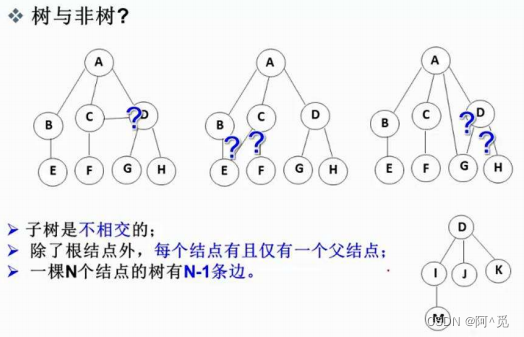
1.2 树的相关概念
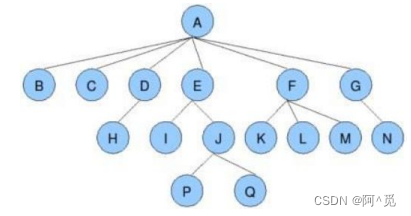
节点的度 :一个节点含有的子树的个数称为该节点的度; 如上图: A 的为 6叶节点或终端节点 :度为 0 的节点称为叶节点; 如上图: B 、 C 、 H 、 I... 等节点为叶节点非终端节点或分支节点 :度不为 0 的节点; 如上图: D 、 E 、 F 、 G... 等节点为分支节点双亲节点或父节点 :若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图: A 是 B 的父节点孩子节点或子节点 :一个节点含有的子树的根节点称为该节点的子节点; 如上图: B 是 A 的孩子节点兄弟节点 :具有相同父节点的节点互称为兄弟节点; 如上图: B 、 C 是兄弟节点树的度 :一棵树中,最大的节点的度称为树的度; 如上图:树的度为 6节点的层次 :从根开始定义起,根为第 1 层,根的子节点为第 2 层,以此类推;树的高度或深度 :树中节点的最大层次; 如上图:树的高度为 4堂兄弟节点 :双亲在同一层的节点互为堂兄弟;如上图: H 、 I 互为兄弟节点节点的祖先 :从根到该节点所经分支上的所有节点;如上图: A 是所有节点的祖先子孙 :以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是 A 的子孙森林 :由 m ( m>0 )棵互不相交的树的集合称为森林;
1.3 树的表示
typedef int DataType;
struct Node
{struct Node* firstChild1; // 第一个孩子结点struct Node* pNextBrother; // 指向其下一个兄弟结点DataType data; // 结点中的数据域
};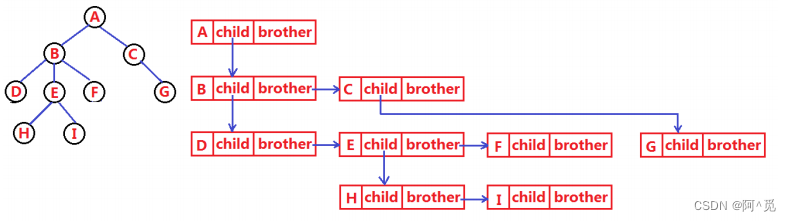
用这个方法,便能方便的表示出所有的节点(俗称左孩子右兄弟)
1.4 树在实际中的运用(表示文件系统的目录树结构)

2.二叉树概念及结构
2.1概念
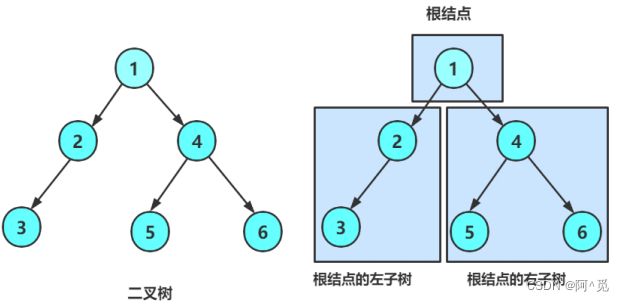
一棵二叉树是结点的一个有限集合,该集合 :1. 要么 为空2. 要么 由一个根节点加上两棵别称为左子树和右子树的二叉树组成
从上图可以看出:1. 二叉树不存在度大于 2 的结点2. 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树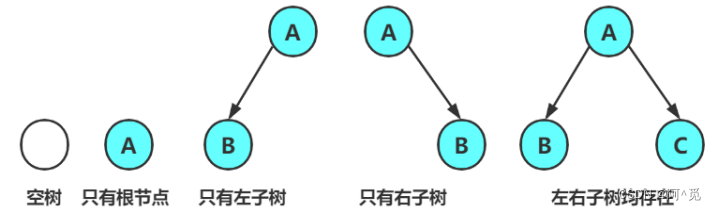 注意 :对于任意的二叉树都是由以上几种情况 复合而成 的
注意 :对于任意的二叉树都是由以上几种情况 复合而成 的
2.2现实中的二叉树:

(我愿称这几棵树为程序员之树)
2.3 特殊的二叉树:
1. 满二叉树 :一个二叉树,如果 每一个层的结点数都达到最大值 ,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K ,且结点总数是,则它就是满二叉树。2. 完全二叉树 :完全二叉树是 效率很高 的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为 K的,有n 个结点的二叉树,当且仅当其每一个结点都与深度为 K 的满二叉树中编号从 1 至n的结点一一对应时称之为完全二叉树。
要注意的是满二叉树是一种特殊的完全二叉树。
2.4 二叉树的性质
1. 若规定根节点的层数为 1 ,则一棵非空二叉树的 第 i 层上最多有2^(i-1)个结点.2. 若规定根节点的层数为 1 ,则 深度为 h 的二叉树的最大结点数是2^h-1.3. 对任何一棵二叉树 , 如果度为0其叶结点个数为, 度为2的分支结点个数为
,则有n0 = n2 +1
4. 若规定根节点的层数为 1 ,具有 n 个结点的满二叉树的深度 , h=. (ps:是log 以 2为底,n+1 为对数 )5. 对于具有 n 个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从 0 开始编号,则对于序号为i 的结点有:1. 若 i>0 , i 位置节点的双亲序号: (i-1)/2 ; i=0 , i 为根节点编号,无双亲节点2. 若 2i+1<n ,左孩子序号: 2i+1 , 2i+1>=n 否则无左孩子3. 若 2i+2<n ,右孩子序号: 2i+2 , 2i+2>=n 否则无右孩子
2.5 二叉树的存储结构
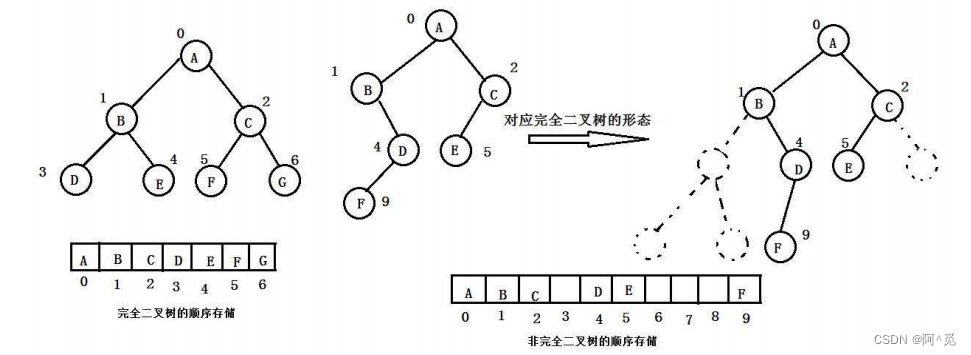
2. 链式存储
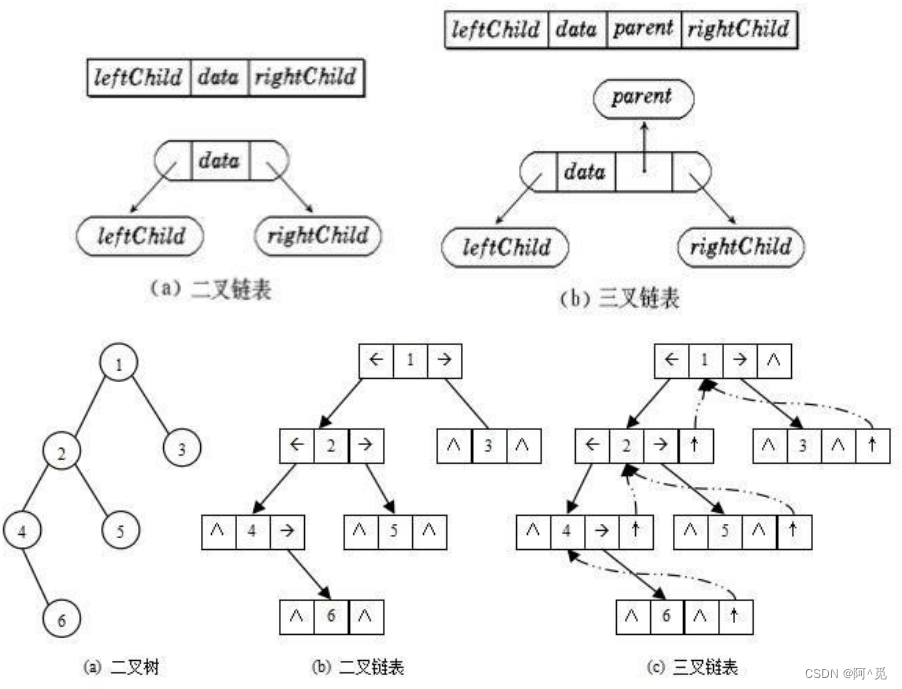
typedef int BTDataType;
// 二叉链
struct BinaryTreeNode
{struct BinTreeNode* pLeft; // 指向当前节点左孩子struct BinTreeNode* pRight; // 指向当前节点右孩子BTDataType data; // 当前节点值域
}// 三叉链
struct BinaryTreeNode
{struct BinTreeNode* pParent; // 指向当前节点的双亲struct BinTreeNode* pLeft; // 指向当前节点左孩子struct BinTreeNode* pRight; // 指向当前节点右孩子BTDataType data; // 当前节点值域
};相关文章:

基本数据结构二叉树(1)
目录 1.树概念及结构 1.1树的概念 1.2 树的相关概念 1.3 树的表示 1.4 树在实际中的运用(表示文件系统的目录树结构) 2.二叉树概念及结构 2.1概念 2.2现实中的二叉树: 2.3 特殊的二叉树: 2.5 二叉树的存储结构 2. 链式存…...
【python】Python将100个PDF文件对应的json文件存储到MySql数据库(源码)【独一无二】
👉博__主👈:米码收割机 👉技__能👈:C/Python语言 👉公众号👈:测试开发自动化【获取源码商业合作】 👉荣__誉👈:阿里云博客专家博主、5…...

Android:Google三方库之Adjust集成详细步骤
通过 Adjust 安卓 SDK,您可以在自己的安卓应用中跟踪归因、事件及更多数据。请按照本指南中说明的步骤操作,在应用内设置 Adjust SDK 1、添加依赖 //adjustimplementation("com.adjust.sdk:adjust-android:4.33.5")implementation("com.…...
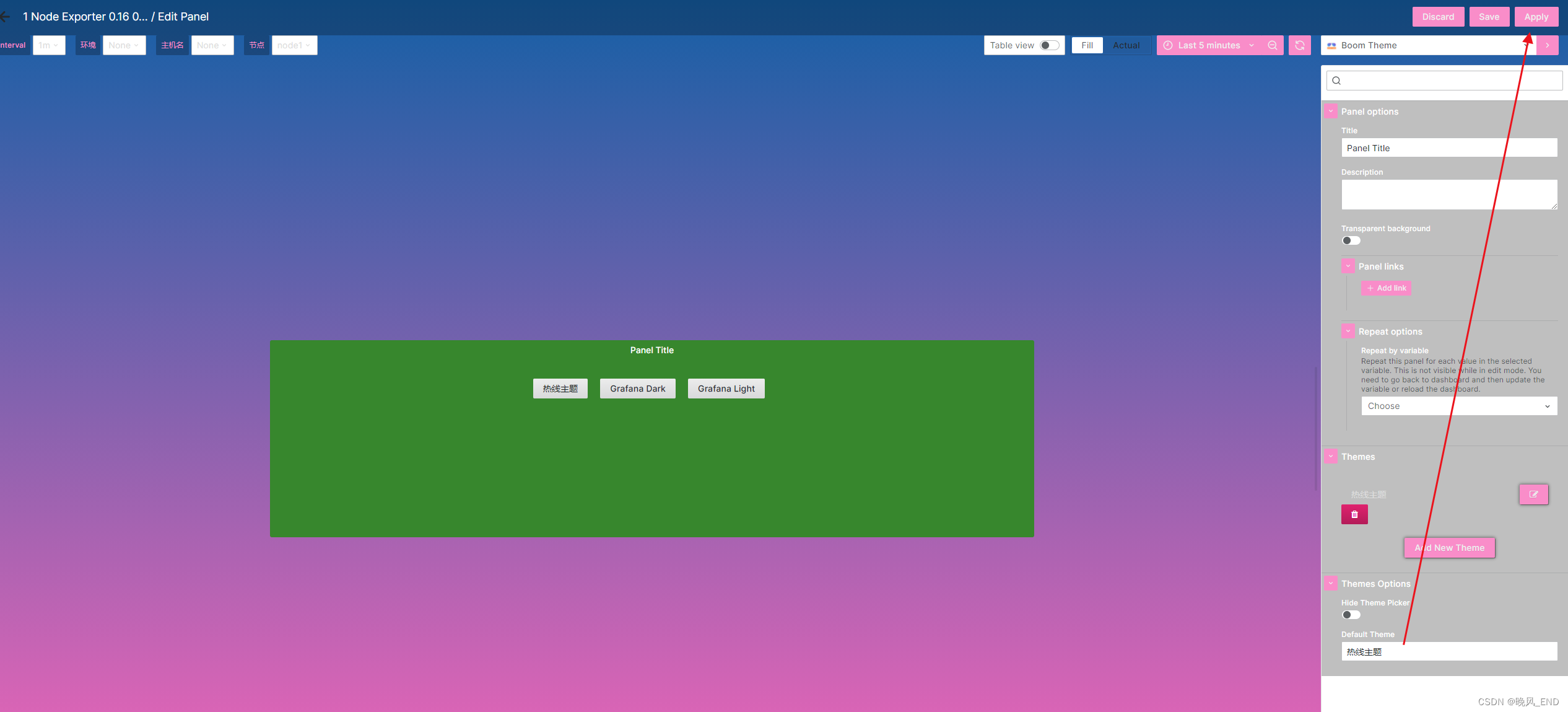
prometheus|云原生|grafana-9.4.3版本的主题更改
一, grafana-9.4.3版本的主题更改 grafana-9.4.3版本应该是目前比较高的版本了,但不知道是什么原因,grafana的主题界面并不多,只有暗色,亮色和系统色三种 配置管理----首选项里可以看到 亮色: 暗色&…...

B033-Servlet交互 JSP
目录 ServletServlet的三大职责跳转:请求转发和重定向请求转发重定向汇总请求转发与重定向的区别用请求转发和重定向完善登录 JSP第一个JSP概述注释设置创建JSP文件默认字符编码集 JSP的java代码书写JSP的原理三大指令九大内置对象改造动态web工程进行示例内置对象名…...
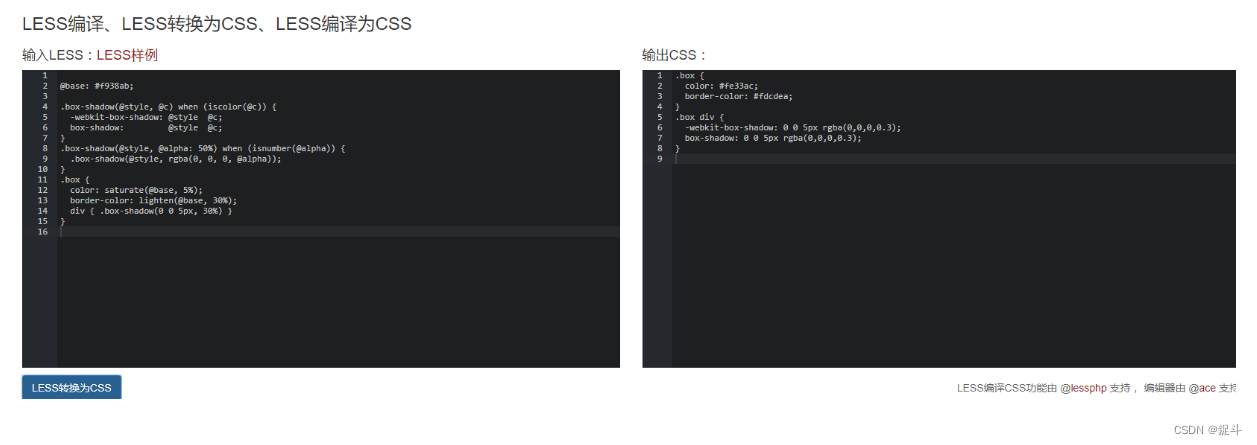
Less 安装教程
文章目录 前言LESS的系统要求安装LESS例子输出Less编译css工具后言 前言 hello world欢迎来到前端的新世界 😜当前文章系列专栏:Sass和Less 🐱👓博主在前端领域还有很多知识和技术需要掌握,正在不断努力填补技术短板…...
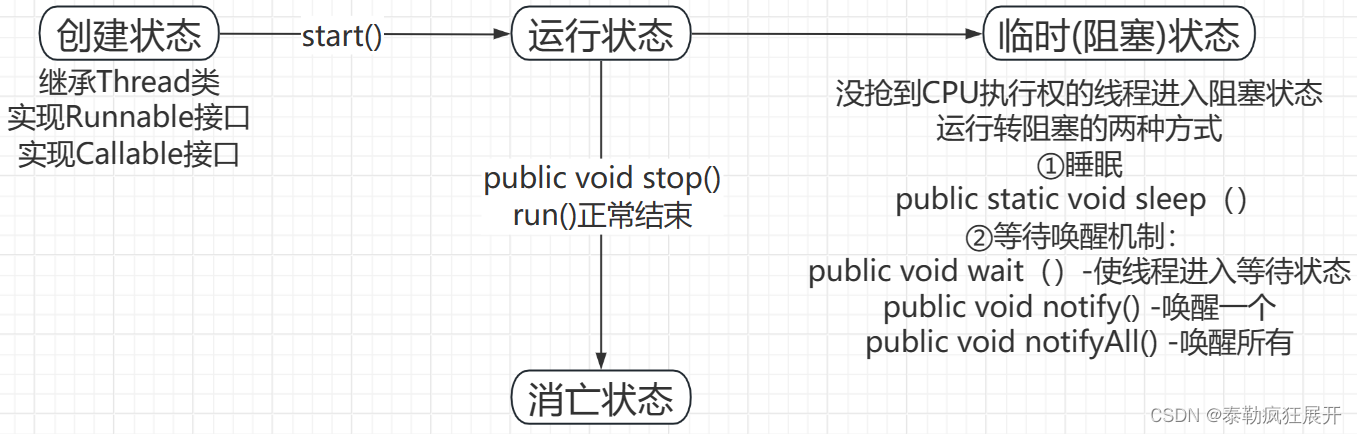
Java研学-多线程
一 名词解析 1 线程 : 控制指定APP(进程)执行的最基本单元(最小单位) 2 进程 : 硬件设备上的每一个应用程序 3 单线程 : 一个进程中只有一个线程执行,实际上基本没有这种情况 4 多线程 : 一个进程中至少有两个或两个以上的线程在执行 二 创建方式 1 共有三种:Thread类. R…...
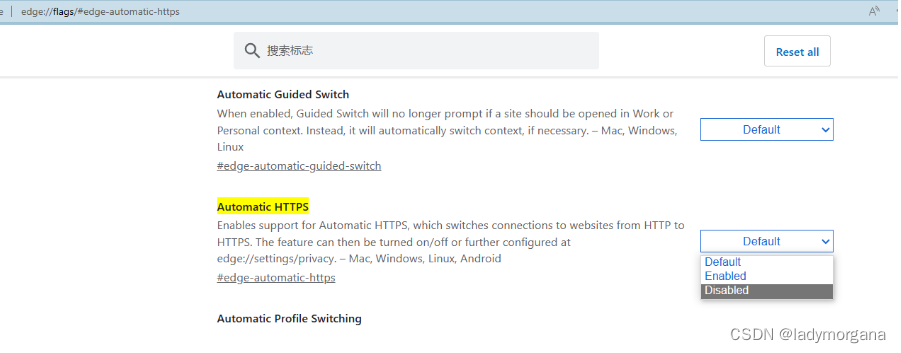
【日常总结】如何禁止浏览器 http自动跳转成https
一、场景 二、问题 三、解决方案 3.1 chrome 浏览器 3.2 edge 浏览器: 3.3 Safari 浏览器 3.4 Firefox 浏览器 3.5 Microsoft Edge 一、场景 公司网站 http:// 谷歌浏览器中自动转换成 https:// 导致无法访问 二、问题 nginx配置ssl 443接口, ht…...
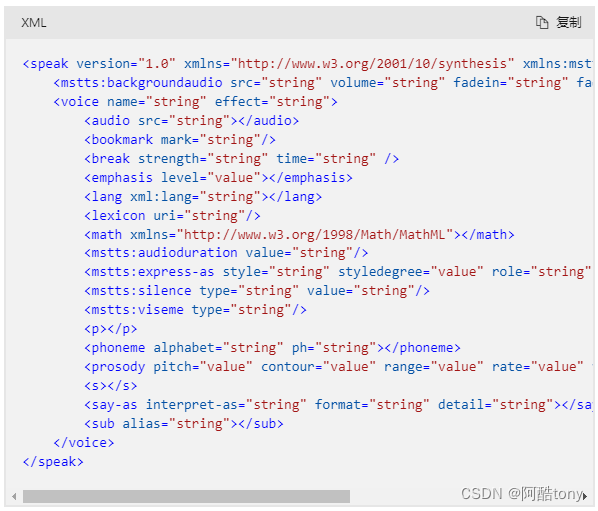
文本转语音:微软语音合成标记语言 (SSML) 文本结构和事件
SSML 的语音服务实现基于万维网联合会的语音合成标记语言版本 1.0。 语音服务支持的元素可能与 W3C 标准不同。 每个 SSML 文档是使用 SSML 元素(或标记)创建的。 这些元素用于调整语音、风格、音节、韵律、音量等。 下面是 SSML 文档的基本结构…...

计算机网络之物理层(数据通信有关)
一、概述 1.1物理层引入的目的 屏蔽掉传输介质的多样性,导致数据传输方式的不同;物理层的引入使得高层看到的数据都是统一的0,1构成的比特流 1.2.物理层如何实现屏蔽 物理层靠定义的不同的通信协议(一般称通信规程) 这些协议…...
)
安卓开发之HTTP API服务接口设计(基于okhttp3请求)
安卓中的请求 OkHttp3 是一个开源的 Java/Android HTTP 客户端库,由 Square 公司开发。它提供了简洁和高效 的 API ,用于进行 HTTP 请求、处理响应以及与服务器进行通信。 以下是 OkHttp3 的一些主要特点和功能: 简单易用: OkHttp3 提供了简洁的 API ,使得发送 HTTP 请求变…...

我的第一次SACC之旅
今年有很多第一次,第一次作为“游客”参加DTCC(中国数据库大会),第一次作为讲师参与ACDU中国行(成都站),第一次参加OB年度发布会(包含DBA老友会),而这次是第一…...
)
Codeforces Round 908 (Div. 2)
Codeforces Round 908 (Div. 2) 文章目录 Codeforces Round 908 (Div. 2)ABCD A 获取对战的最后一个即为胜者 #include <bits/stdc.h>using namespace std;void solve() {int n;cin >> n;string s;cin >> s;cout << s[n-1] << endl; }int main…...
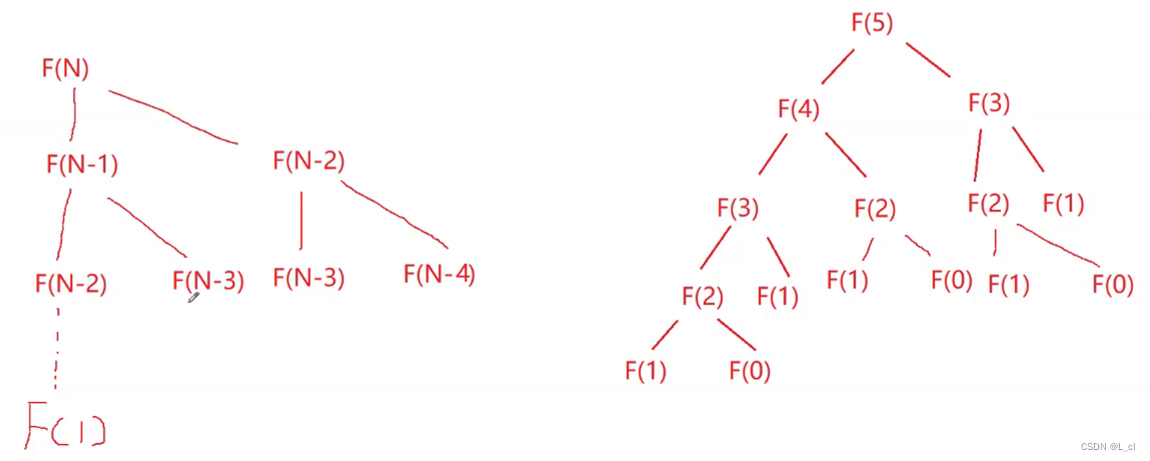
Java实现-数据结构 2.时间和空间复杂度
.如何衡量一个算法的好坏:时间复杂度和空间复杂度 算法效率分为时间效率和空间效率,时间效率称为时间复杂度,空间效率称为空间复杂度 时间复杂度 算法的时间复杂度是一个数学函数,它描述了算法的运行时间,一个算法执…...

Docker exec命令
docker exec :在运行的容器中执行命令。 语法: docker exec [OPTIONS] CONTAINER COMMAND [ARG...]OPTIONS说明: -d:分离模式: 在后台运行 -i:即使没有附加也保持STDIN打开 -t:分配一个伪终…...

可燃气体监测仪助力燃气管网安全监测,效果一览
城市地下管线是指城市范围内供应水、排放水、燃气等各类管线及其附属设施,它们是保障城市正常运转的重要基础设施且影响着城市生命线。其中燃气引发的事故近些年不断增加,由于燃气管线深埋地下环境复杂,所以仅仅依赖人工巡查难以全面有效地防…...
在WSL搭建Schema Registry)
Kafka(二)在WSL搭建Schema Registry
目录 1 Avro与Schema Registry2 搭建Schema Registry2.1 下载Confluent并解压2.2 设置环境变量2.3 修改配置2.4 启动服务 3 API列表 1 Avro与Schema Registry Apache Avro 是一种高效的数据序列化系统,用于在不同的应用程序和平台之间传输和存储数据。它提供了一种…...
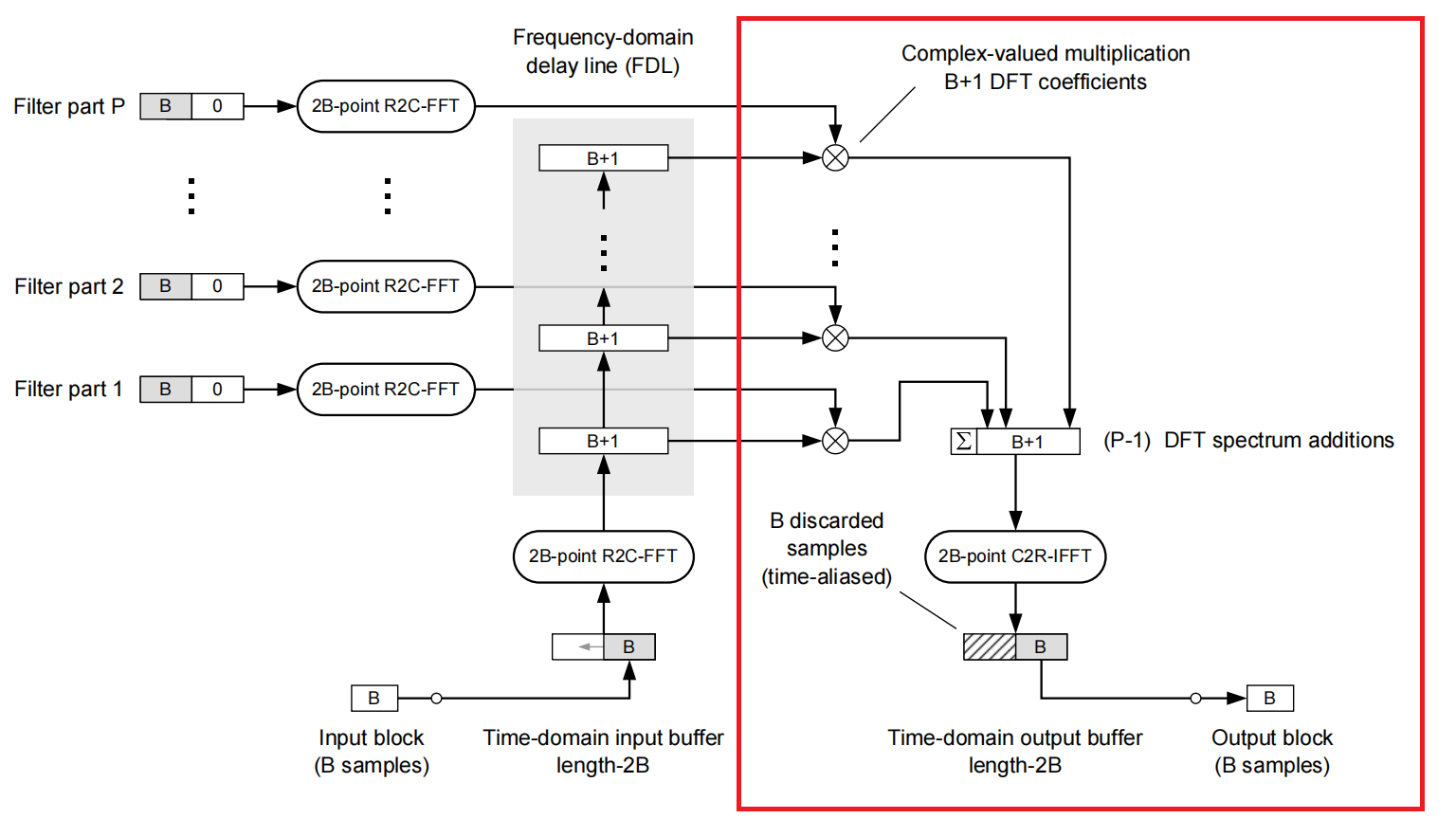
webrtc AEC 线性滤波 PBFDAF(均匀分块频域自适应滤波)介绍
计算一个脉冲响应和输入信号的卷积,除了使用原始的时域卷积以外,还有如下方法: FFT卷积的方法:对输入信号(长度M)和脉冲响应(长度N)分别补零到K(K>MN-1),…...

开源vs闭源,处在大模型洪流中,向何处去?
文章目录 一、开源和闭源的优劣势比较1.1 开源优势1.2 闭源的优势 二、开源和闭源对大模型技术发展的影响2.1 数据共享2.2 算法创新2.3 业务拓展2.4 安全性和隐私2.5 社会责任和伦理 三、开源与闭源的商业模式比较3.1 盈利模式3.2 市场竞争3.3 用户生态3.4 创新速度 四…...

web前端之vue和echarts的堆叠柱状图顶部显示总数、鼠标悬浮工具提示、设置图例的显示与隐藏、label、legend、tooltip
MENU 效果图htmlJavaScripstyle解析 效果图 html <template><div><div><div id"idStackedColumnChart" style"width: 100%; height: 680px"></div></div></div> </template>JavaScrip export default {…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...