python:傅里叶分析,傅里叶变换 FFT
使用python进行傅里叶分析,傅里叶变换 FFT 的一些关键概念的引入:
1.1.离散傅里叶变换(DFT)
离散傅里叶变换(discrete Fourier transform) 傅里叶分析方法是信号分析的最基本方法,傅里叶变换是傅里叶分析的核心,经过它把信号从时间域变换到频率域,进而研究信号的频谱结构和变化规律。可是它的致命缺点是:计算量太大,时间复杂度过高,当采样点数过高的时候,计算缓慢,由此出现了DFT的快速实现,即下面的快速傅里叶变换FFT。
1.2.快速傅里叶变换(FFT)
计算量更小的离散傅里叶的一种实现方法。快速傅氏变换(FFT),是离散傅氏变换的快速算法,它是根据离散傅氏变换的奇、偶、虚、实等特性,对离散傅立叶变换的算法进行改进获得的。
1.3.采样频率以及采样定率
采样频率,也称为采样速度或者采样率,定义了每秒从连续信号中提取并组成离散信号的采样个数,它用赫兹(Hz)来表示。采样频率的倒数是采样周期或者叫做采样时间,它是采样之间的时间间隔。通俗的讲采样频率是指计算机每秒钟采集多少个信号样本。
采样定理 ,又称香农采样定理,奈奎斯特采样定理,是信息论,特别是通信与信号处理学科中的一个重要基本结论。采样定理指出,若是信号是带限的,而且采样频率高于信号带宽的两倍,那么,原来的连续信号能够从采样样本中彻底重建出来。
1.4.如何理解采样定理
在对连续信号进行离散化的过程当中,不免会损失不少信息,就拿一个简单地正弦波而言,若是我1秒内就选择一个点,很显然,损失的信号太多了,光着一个点我根本不知道这个正弦信号究竟是什么样子的,天然也没有办法根据这一个采样点进行正弦波的还原,很明显,我采样的点越密集,那越接近原来的正弦波原始的样子,天然损失的信息越少,越方便还原正弦波。
采样定理说明采样频率与信号频率之间的关系,是连续信号离散化的基本依据。 它为采样率创建了一个足够的条件,该采样率容许离散采样序列从有限带宽的连续时间信号中捕获全部信息。
编写 test_fft_1.py 如下
# -*- coding: utf-8 -*-
""" 使用scipy包实现快速傅里叶变换 """
import numpy as np
from scipy.fftpack import fft, ifft
import matplotlib.pyplot as plt
from matplotlib.pylab import mpl
mpl.rcParams['font.sans-serif'] = ['SimHei'] #显示中文
mpl.rcParams['axes.unicode_minus'] = False #显示负号# 采样点选择1400个,由于设置的信号频率份量最高为600赫兹,根据采样定理知采样频率要大于信号频率2倍,
# 因此这里设置采样频率为1400赫兹(即一秒内有1400个采样点,同样意思的)
x = np.linspace(0,1,1400)
#设置须要采样的信号,频率份量有200,400和600
y = 7*np.sin(2*np.pi*200*x) + 5*np.sin(2*np.pi*400*x) + 3*np.sin(2*np.pi*600*x)
fft_y = fft(y) #快速傅里叶变换
N= 1400
x = np.arange(N) # 频率个数
half_x = x[range(int(N/2))] #取一半区间
abs_y = np.abs(fft_y) # 取复数的绝对值,即复数的模(双边频谱)
angle_y = np.angle(fft_y) #取复数的角度
normalization_y = abs_y/N #归一化处理(双边频谱)
normalization_half_y = normalization_y[range(int(N/2))] #因为对称性,只取一半区间(单边频谱)
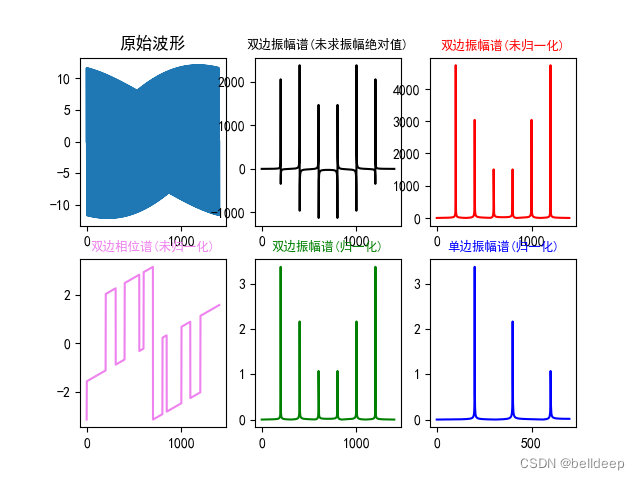
plt.subplot(231)
plt.plot(x,y)
plt.title('原始波形')
plt.subplot(232)
plt.plot(x,fft_y,'black')
plt.title('双边振幅谱(未求振幅绝对值)',fontsize=9,color='black')
plt.subplot(233)
plt.plot(x,abs_y,'r')
plt.title('双边振幅谱(未归一化)',fontsize=9,color='red')
plt.subplot(234)
plt.plot(x,angle_y,'violet')
plt.title('双边相位谱(未归一化)',fontsize=9,color='violet')
plt.subplot(235)
plt.plot(x,normalization_y,'g')
plt.title('双边振幅谱(归一化)',fontsize=9,color='green')
plt.subplot(236)
plt.plot(half_x,normalization_half_y,'blue')
plt.title('单边振幅谱(归一化)',fontsize=9,color='blue')
plt.show()
运行 python test_fft_1.py
傅里叶定理指出,任何频率为f0的周期信号都可以通过将频率为f0,2f0,3f0,4f0,5f0等的“正弦波”(正弦波)相加而精确地构建。将周期时域信号分割为正弦波称为傅里叶分析。
“傅里叶级数”中的每个正弦曲线的特征在于频率振幅,以及阶段f0被称为基频。
2f0、3f0、4f0等被称为谐波。
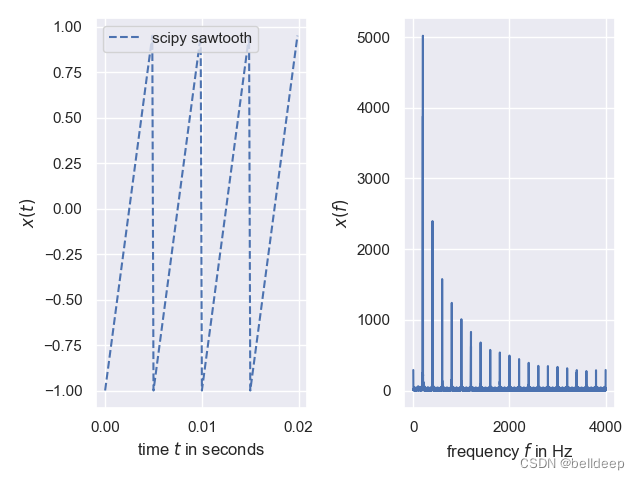
编写 test_sawtooth.py 如下
# -*- coding: utf-8 -*-
"""使用scipy中的 sawtooth()生成了频率为f=200Hz的锯齿信号,持续时间为2秒。"""
import matplotlib.pyplot as plt # plotting
import seaborn as sns # styling (uncomment if you want)
import numpy as np
from scipy import signal as sig # for easy sawtooth signal generationsns.set()
fs=8000 # sampling frequency
t = np.arange(0, 2, 1/fs) # time vector
f = 200 # frequency in Hz for scipy sawtooth
saw_tooth = sig.sawtooth(2 * np.pi * f * t)
# plot first 20 ms (=160 samples at sampling frequency of 8000 Hz)
plt.subplot(1,2,1)
plt.plot(t[0:160], saw_tooth[0:160], '--', label='scipy sawtooth')
plt.xlabel('time $t$ in seconds')
plt.ylabel('$x(t)$')
plt.legend()# calculate the spectum (frequency domain representation)
FFT_length = 2**15 # take a power of two which is larger than the signal length
f = np.linspace(0, fs/2, num=int(FFT_length/2+1))
spectrum = np.abs(np.fft.rfft(saw_tooth, n=FFT_length))
# plot the spectrum
plt.subplot(1,2,2)
plt.plot(f,spectrum)
plt.xlabel('frequency $f$ in Hz')
plt.ylabel('$x(f)$')
plt.tight_layout() # this allowes for some space for the title text.
plt.show()运行 pytho test_sawtooth.py
相关文章:

python:傅里叶分析,傅里叶变换 FFT
使用python进行傅里叶分析,傅里叶变换 FFT 的一些关键概念的引入: 1.1.离散傅里叶变换(DFT) 离散傅里叶变换(discrete Fourier transform) 傅里叶分析方法是信号分析的最基本方法,傅里叶变换是傅里叶分析的核心&…...

云原生系列Go语言篇-编写测试Part 2
基准测试 确定代码是快或慢非常复杂。我们不用自己计算,应使用Go测试框架内置的基准测试。下面来看第15章的GitHub代码库sample_code/bench目录下的函数: func FileLen(f string, bufsize int) (int, error) {file, err : os.Open(f)if err ! …...

CMake Error:No targets specified and no makefile found
在适用cmake构建项目的时候,突然遇到了这个报错 Make Error at CMakeLists.txt:1 (project): VERSION not allowed unless CMP0048 is set to NEW – Configuring incomplete, errors occurred! make: *** No targets specified and no makefile found. Stop. CMake…...

常见树种(贵州省):019滇白珠、杜茎山、苍山越桔、黄背越桔、贵州毛柃、半齿柃、钝叶柃、细枝柃、细齿叶柃木、土蜜树、山矾、胡颓子、檵木
摘要:本专栏树种介绍图片来源于PPBC中国植物图像库(下附网址),本文整理仅做交流学习使用,同时便于查找,如有侵权请联系删除。 图片网址:PPBC中国植物图像库——最大的植物分类图片库 一、滇白珠…...

java - 定时器
一、什么是定时器 定时器是指可以通过 Java 中的 Timer 类和 TimerTask 类所提供的功能来实现定期执行某些任务的工具。 标准库中提供了一个 Timer 类 . Timer 类的核心方法为 schedule . schedule 包含两个参数 . 第一个参数指定即将要执行的任务代码 , 第二个参数指定多…...

jQuery【菜单功能、淡入淡出轮播图(上)、淡入淡出轮播图(下)、折叠面板】(五)-全面详解(学习总结---从入门到深化)
目录 菜单功能 淡入淡出轮播图(上) 淡入淡出轮播图(下) 折叠面板 菜单功能 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEedge"><…...

攻防非对称问题| 当前企业面临的网络攻防非对称问题及其解决途径
随着信息技术的不断发展,网络已经成为我们日常生活和商业活动中不可或缺的一部分。然而,随之而来的是网络安全问题的不断升级。网络攻防非对称问题是当前亟待解决的一个复杂而严峻的挑战。其主要的表现是攻击成本远低于防御成本以及相同投入带来的攻击能…...

Java多线程二-线程安全
1、线程安全问题 多个线程,同时操作同一个共享资源的时候,可能会出现业务安全问题。 2、实例:取钱的线程安全问题 2.1、场景 小明和小红是夫妻,他们有个共同账户,余额是十万元,如果两人同时取钱并且各自取…...

Rust个人学习之结构体
第一反应,Rust结构体跟python的很像,不知道感觉对不对; 书中提到第一反应,Rust结构体跟python的很像,不知道感觉对不对; 书中提到:结构体是一种自定义数据类型,它允许命名多个相关的…...

kafka详细讲解与安装
Kafka是一种分布式流处理平台,具有高吞吐量、可扩展性和容错性。它最初由LinkedIn开发,现已成为Apache软件基金会的顶级项目。Kafka广泛应用于实时数据流处理、日志收集、消息队列等场景。 以下是关于Kafka的简要讲解和安装步骤: 一、Kafka…...

在我国干独立游戏开发有多难?
游戏独立开发在中国,一直以来都是一条充满挑战的道路。尽管有着无限的激情和创意,但面对市场、资金、政策等多方面的困难,许多独立开发者在这条路上艰难前行。 首先,市场竞争激烈是中国游戏独立开发者面临的首要挑战。随着游戏产…...

不可错过的网上宝藏:2023年必看的顶级资源大盘点!
亲爱的“AI uTools”读者们,大家好! 在这个信息爆炸的时代,互联网上充满了无数的资源,但如何从这海量信息中挑选出真正有用的宝藏呢?今天,我为大家精心挑选了一系列优质网站资源,涵盖了从文本处…...

日本服务器访问速度和带宽有没有直接关系?
对于许多网站和应用程序来说,服务器的访问速度是至关重要的。用户希望能够快速加载页面、上传和下载文件,而这些都与服务器的带宽有关。那么,日本服务器的访问速度和带宽之间是否存在直接关系呢? 我们需要了解什么是带宽。带宽是指网络…...

[vxe-table] vxe-table-column配合v-if导致列样式与位置错乱
<vxe-table-column v-if"pageInfo.id 4 ||pageInfo.id 8" title"上报类型" width"100" key1><template v-slot"{row}"><span>咨询工具</span></template> </vxe-table-column>//或者<vxe-ta…...

C# 忽略大小写
在 C# 中,你可以通过以下几种方式来忽略大小写: 使用 ToLower 或 ToUpper 方法将字符串转换为全小写或全大写,然后进行比较。使用 Compare 或 CompareOrdinal 方法,并传入正确的 StringComparer 实例以指示比较应该忽略大小写。使…...

大数据技术之数据安全与网络安全——CMS靶场(文章管理系统)实训
大数据技术之数据安全与网络安全——CMS靶场(文章管理系统)实训 在当今数字化时代,大数据技术的迅猛发展带来了前所未有的数据增长,同时也催生了对数据安全和网络安全的更为迫切的需求。本篇博客将聚焦于大数据技术背景下的数据安全与网络安全ÿ…...

[datastore@cyberfear.com].Elbie、[thekeyishere@cock.li].Elbie勒索病毒数据怎么处理|数据解密恢复
引言: 随着科技的进步,勒索病毒变得越来越复杂,而[datastorecyberfear.com].Elbie、[thekeyisherecock.li].Elbie勒索病毒是其中的一种令人头疼的威胁。本文将深入介绍[datastorecyberfear.com].Elbie、[thekeyisherecock.li].Elbie勒索病毒…...

【咕咕送书 | 第六期】深入浅出阐述嵌入式虚拟机原理,实现“小而能”嵌入式虚拟机!
🎬 鸽芷咕:个人主页 🔥 个人专栏:《粉丝福利》 《linux深造日志》 ⛺️生活的理想,就是为了理想的生活! 文章目录 ⛳️ 写在前面参与规则引言一、为什么嵌入式系统需要虚拟化技术?1.1 专家推荐 二、本书适合谁&#x…...
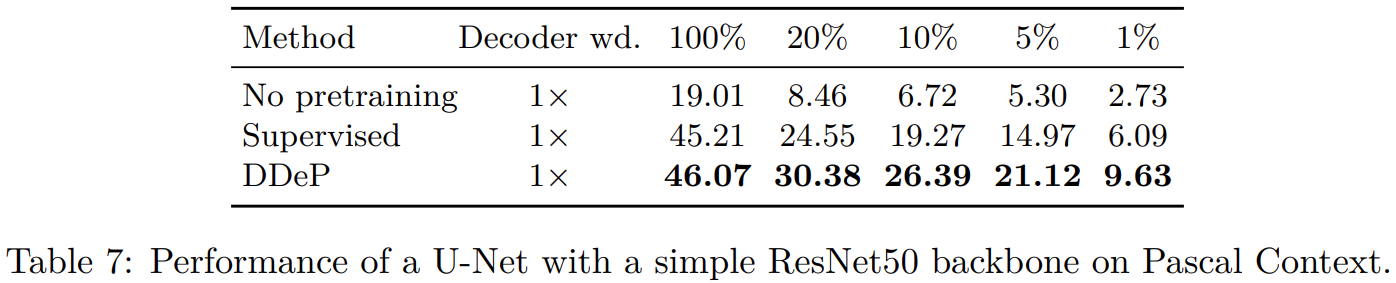
论文阅读——DDeP(cvpr2023)
分割标签耗时且贵,所以常常使用预训练提高分割模型标签有效性,反正就是,需要一个预训练分割模型。典型的分割模型encoder部分通过分类任务预训练,decoder部分参数随机初始化。作者认为这个方法次优,尤其标签比较少的情…...

Docker | Docker常用命令
Docker | Docker常用命令 ✅作者简介:大家好,我是Leo,热爱Java后端开发者,一个想要与大家共同进步的男人😉😉 🍎个人主页:Leo的博客 💞当前专栏:Docker系列 ✨…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...

0x-3-Oracle 23 ai-sqlcl 25.1 集成安装-配置和优化
是不是受够了安装了oracle database之后sqlplus的简陋,无法删除无法上下翻页的苦恼。 可以安装readline和rlwrap插件的话,配置.bahs_profile后也能解决上下翻页这些,但是很多生产环境无法安装rpm包。 oracle提供了sqlcl免费许可,…...
