C# 忽略大小写
在 C# 中,你可以通过以下几种方式来忽略大小写:
- 使用 ToLower 或 ToUpper 方法将字符串转换为全小写或全大写,然后进行比较。
- 使用 Compare 或 CompareOrdinal 方法,并传入正确的 StringComparer 实例以指示比较应该忽略大小写。
- 使用 Equals 方法并将 StringComparison.CurrentCultureIgnoreCase 或 StringComparison.OrdinalIgnoreCase 作为参数传递给它。
- 如果你在使用 LINQ 进行查询,你可以使用 .ToLower() 或 .ToUpper() 方法在查询语句中忽略大小写。
- 在使用正则表达式时,可以使用 RegexOptions.IgnoreCase 标志来忽略大小写。
另外,还有一些内置的方法,例如 Contains 和 StartsWith 等,它们也提供了忽略大小写的重载版本。
例如1:
使用String.Equals方法并设置其ignoreCase参数为true。
string str1 = "Hello World";
string str2 = "hello world"; if (String.Equals(str1, str2, StringComparison.OrdinalIgnoreCase))
{ Console.WriteLine("Strings are equal.");
}
else
{ Console.WriteLine("Strings are not equal.");
}在上述代码中,StringComparison.OrdinalIgnoreCase是一个枚举值,它告诉String.Equals方法忽略大小写。如果两个字符串在忽略大小写的情况下相等,那么这个方法就会返回true。
此外,如果你想在字符串操作中普遍忽略大小写,你可能需要将所有字符串都转化为大写或小写,然后再进行比较。
例如2:
string str1 = "Hello World".ToUpper();
string str2 = "hello world".ToUpper(); if (str1 == str2)
{ Console.WriteLine("Strings are equal.");
}
else
{ Console.WriteLine("Strings are not equal.");
}在这个例子中,我们使用ToUpper方法将所有字符串转化为大写,然后再进行比较。这样就可以在不考虑大小写的情况下比较字符串了。
相关文章:

C# 忽略大小写
在 C# 中,你可以通过以下几种方式来忽略大小写: 使用 ToLower 或 ToUpper 方法将字符串转换为全小写或全大写,然后进行比较。使用 Compare 或 CompareOrdinal 方法,并传入正确的 StringComparer 实例以指示比较应该忽略大小写。使…...

大数据技术之数据安全与网络安全——CMS靶场(文章管理系统)实训
大数据技术之数据安全与网络安全——CMS靶场(文章管理系统)实训 在当今数字化时代,大数据技术的迅猛发展带来了前所未有的数据增长,同时也催生了对数据安全和网络安全的更为迫切的需求。本篇博客将聚焦于大数据技术背景下的数据安全与网络安全ÿ…...

[datastore@cyberfear.com].Elbie、[thekeyishere@cock.li].Elbie勒索病毒数据怎么处理|数据解密恢复
引言: 随着科技的进步,勒索病毒变得越来越复杂,而[datastorecyberfear.com].Elbie、[thekeyisherecock.li].Elbie勒索病毒是其中的一种令人头疼的威胁。本文将深入介绍[datastorecyberfear.com].Elbie、[thekeyisherecock.li].Elbie勒索病毒…...

【咕咕送书 | 第六期】深入浅出阐述嵌入式虚拟机原理,实现“小而能”嵌入式虚拟机!
🎬 鸽芷咕:个人主页 🔥 个人专栏:《粉丝福利》 《linux深造日志》 ⛺️生活的理想,就是为了理想的生活! 文章目录 ⛳️ 写在前面参与规则引言一、为什么嵌入式系统需要虚拟化技术?1.1 专家推荐 二、本书适合谁&#x…...
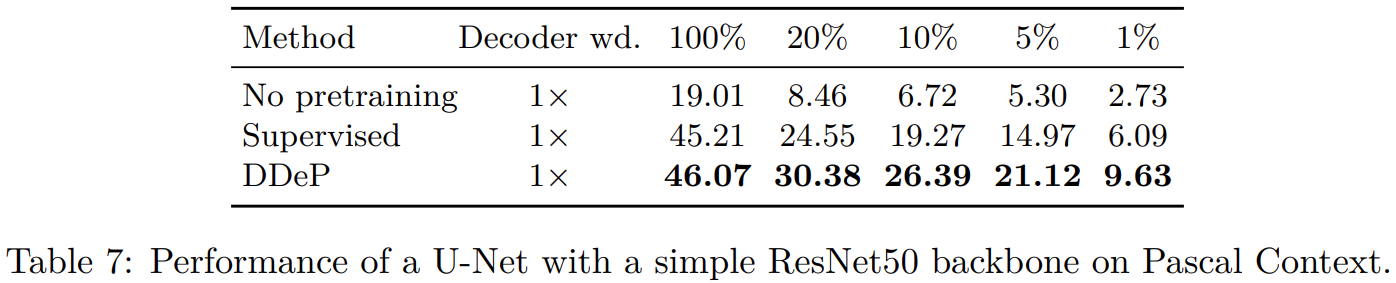
论文阅读——DDeP(cvpr2023)
分割标签耗时且贵,所以常常使用预训练提高分割模型标签有效性,反正就是,需要一个预训练分割模型。典型的分割模型encoder部分通过分类任务预训练,decoder部分参数随机初始化。作者认为这个方法次优,尤其标签比较少的情…...

Docker | Docker常用命令
Docker | Docker常用命令 ✅作者简介:大家好,我是Leo,热爱Java后端开发者,一个想要与大家共同进步的男人😉😉 🍎个人主页:Leo的博客 💞当前专栏:Docker系列 ✨…...

精进:简单聊聊华为战略与DSTE
首发:麦子禾 作者:石头 在以前专题文中,石头聊华为市场管理MM、基于价值驱动的业务设计VDBD、轻量级战略流程五看三定、业务领先模型BLM、业务执行力模型BEM比较多,印象中石头没有具体谈过DSTE(从战略规划到执行&…...
强制删除文件
DEL /F /A /Q \\?\%1 RD /S /Q \\?\%1 强制删除文件,新建一个文本文件,将以上代码复制到文档中,保存,将文档重命名为delete.bat 如果弹窗提示修改后缀名可能导致文件不可用,也点击确认修改文件名称. 将需要强制删除的文件拖拽到这个delete.bat文件上,显示使用delete.bat打…...

Vue+ElementUI+C#技巧分享:周数选择器
文章目录 前言一、周数的计算逻辑1.1 周数的定义1.2 年初周数的确定1.3 周数的计算方法 二、VueElementUI代码实现2.1 计算周数2.2 获取周的日期范围2.3 根据周数获取日期范围2.4 控件引用2.4.1 控件引用代码分析2.4.2 初始化变量代码分析 2.5 周数选择器完整代码 三、C#后端代…...
【算法】FFT-1(递归实现)(不包括IFFT)
FFT 多项式多项式乘法复数及运算导数泰勒公式及展开式欧拉公式单位根 FFTCode IFFT 多项式 我们从课本中可以知道,一个 n − 1 n-1 n−1 次的多项式可以写成 a 0 a 1 x a 2 x 2 a 3 x 3 ⋯ a n − 1 x n − 1 a_{0}a_{1}xa_{2}x^2a_{3}x^3\dotsa_{n-1}x^{n-…...

大模型训练效率提升至2.6倍,腾讯Angel机器学习框架升级
在算力紧缺的背景下,如何提升大模型训练和推理的效率,并降低成本,成为业界关注的焦点。 11月23日,腾讯披露,腾讯混元大模型背后的自研机器学习框架Angel再次升级,大模型训练效率提升至主流开源框架的2.6倍…...

【方块消消乐】方块消除游戏-微信小程序开发流程详解
有做过俄罗斯方块游戏小程序的经验,这次有做了一个消灭方块的游戏,实现过程很顺利,游戏看着和之前做的俄罗斯方块游戏很像,这里调整了玩法,试玩感觉还可以,接下来给大家讲一讲消灭方块游戏开发过程。 俄罗斯…...

mybatis配置文件中配置类型别名的方式
在MyBatis配置文件(通常是mybatis-config.xml)中,可以通过以下方式配置类型别名: 1. 使用typeAliases元素配置全局类型别名 <configuration> <typeAliases> <typeAlias alias"YourAlias" type"…...

leetcode目标和
给你一个非负整数数组 nums 和一个整数 target 。 向数组中的每个整数前添加 ‘’ 或 ‘-’ ,然后串联起所有整数,可以构造一个 表达式 : 例如,nums [2, 1] ,可以在 2 之前添加 ‘’ ,在 1 之前添加 ‘-…...
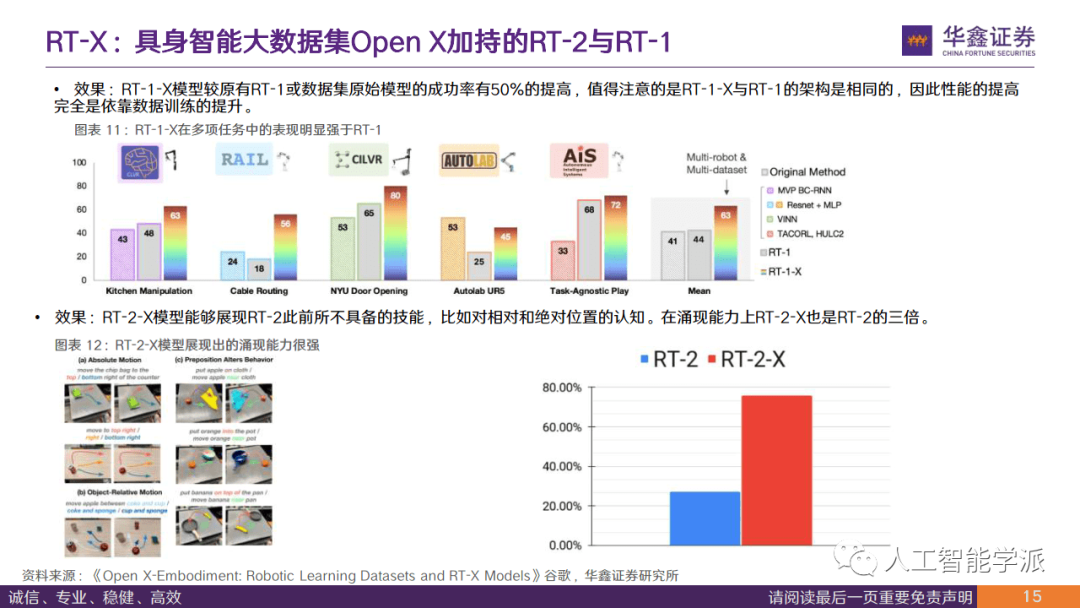
2023人形机器人行业海外科技研究:从谷歌看机器人大模型进展
今天分享的是人形机器人系列深度研究报告:《2023人形机器人行业海外科技研究:从谷歌看机器人大模型进展》。 (报告出品方:华鑫证券) 报告共计:26页 大模型是人形机器人的必备要素 长期来看,人…...

【深度学习笔记】01 数据操作与预处理
01 数据操作与预处理 一、数据操作1.1 基本数据操作1.2 广播机制1.3 索引和切片1.4 节省内存1.5 转换为其他Python对象 二、数据预处理读取数据集处理缺失值转换为张量格式练习 一、数据操作 1.1 基本数据操作 导入torch import torch张量表示一个由数值组成的数组ÿ…...

Python与设计模式--门面模式
8-Python与设计模式–门面模式 一、火警报警器(1) 假设有一组火警报警系统,由三个子元件构成:一个警报器,一个喷水器, 一个自动拨打电话的装置。其抽象如下: class AlarmSensor:def run(self):…...
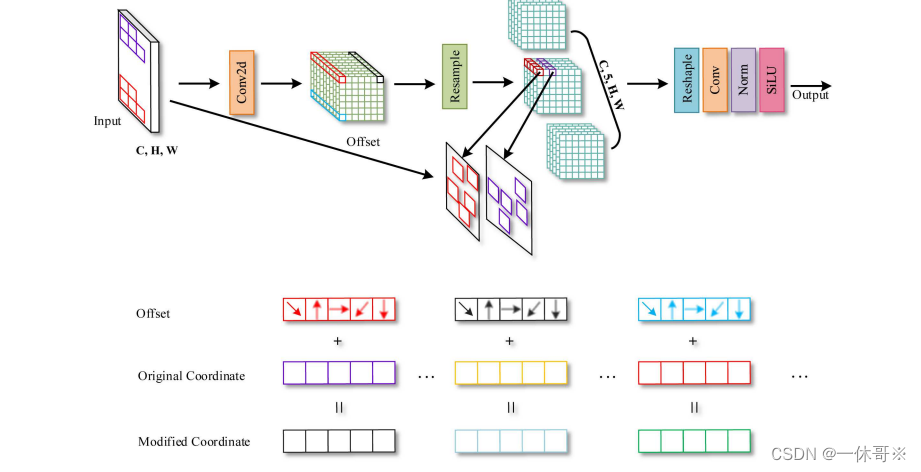
改进YOLOv8 | YOLOv5系列:RFAConv续作,即插即用具有任意采样形状和任意数目参数的卷积核AKCOnv
RFAConv续作,构建具有任意采样形状的卷积AKConv 一、论文yolov5加入的方式论文 源代码 一、论文 基于卷积运算的神经网络在深度学习领域取得了显著的成果,但标准卷积运算存在两个固有缺陷:一方面,卷积运算被限制在一个局部窗口,不能从其他位置捕获信息,并且其采样形状是…...
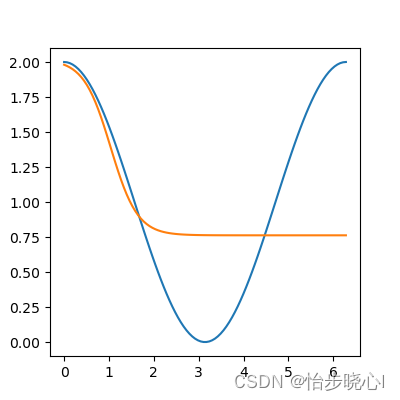
机器学习-激活函数的直观理解
机器学习-激活函数的直观理解 在机器学习中,激活函数(Activation Function)是用于引入非线性特性的一种函数,它在神经网络的每个神经元上被应用。 如果不使用任何的激活函数,那么神经元的响应就是wxb,相当…...
Fedora 36 ARM 镜像源更换与软件安装
1、什么是Fedora Fedora Linux是较具知名度的Linux发行套件之一,由Fedora专案社群开发、红帽公司赞助,目标是建立一套新颖、多功能并且自由的作业系统。 Fedora是商业化的Red Hat Enterprise Linux发行版的上游原始码。 2、Fedora软件安装 64 位 .deb&a…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

6️⃣Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙
Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙 一、前言:离区块链还有多远? 区块链听起来可能遥不可及,似乎是只有密码学专家和资深工程师才能涉足的领域。但事实上,构建一个区块链的核心并不复杂,尤其当你已经掌握了一门系统编程语言,比如 Go。 要真正理解区…...
