leetcode目标和
给你一个非负整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 ‘+’ 或 ‘-’ ,然后串联起所有整数,可以构造一个 表达式 :
例如,nums = [2, 1] ,可以在 2 之前添加 ‘+’ ,在 1 之前添加 ‘-’ ,然后串联起来得到表达式 “+2-1” 。
返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。
示例 1:
输入:nums = [1,1,1,1,1], target = 3
输出:5
解释:一共有 5 种方法让最终目标和为 3 。
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3
示例 2:
输入:nums = [1], target = 1
输出:1
提示:
1 <= nums.length <= 20
0 <= nums[i] <= 1000
0 <= sum(nums[i]) <= 1000
-1000 <= target <= 1000
设dp[i][j]为前i个数字组合为j的个数,则易知前i个字母组合的结果只是在前i-1个字母的组合结果上加减nums[i],所以存在dp[i][j]+=dp[i-1][j-nums[i]];dp[i][j]+=dp[i-1][j-nums[i]]
最优子结构:dp[i][j]
状态转移方程:dp[i][j]+=dp[i-1][j-nums[i]];dp[i][j]+=dp[i-1][j-nums[i]]
注意:因为j不能为负数,所以需要通过加上nums的累加值
int findTargetSumWays(vector<int> &nums, int target) {int l = nums.size(), sum = 0;for (int i = 0; i < l; ++i) {sum += nums[i];}if (target>sum||target<-sum){return 0;}int dp[25][2020] = {0};//dp[i][j] 前i个数组成j的方法个数int len = sum * 2 + 1;dp[0][nums[0] + sum] += 1;dp[0][-nums[0] + sum] += 1;for (int i = 1; i < l; ++i) {for (int j = 0; j <= len; ++j) {if (dp[i - 1][j] != 0) {dp[i][j + nums[i]] += dp[i - 1][j];dp[i][j - nums[i]] += dp[i - 1][j];}}}return dp[l - 1][target + sum];
}
相关文章:

leetcode目标和
给你一个非负整数数组 nums 和一个整数 target 。 向数组中的每个整数前添加 ‘’ 或 ‘-’ ,然后串联起所有整数,可以构造一个 表达式 : 例如,nums [2, 1] ,可以在 2 之前添加 ‘’ ,在 1 之前添加 ‘-…...
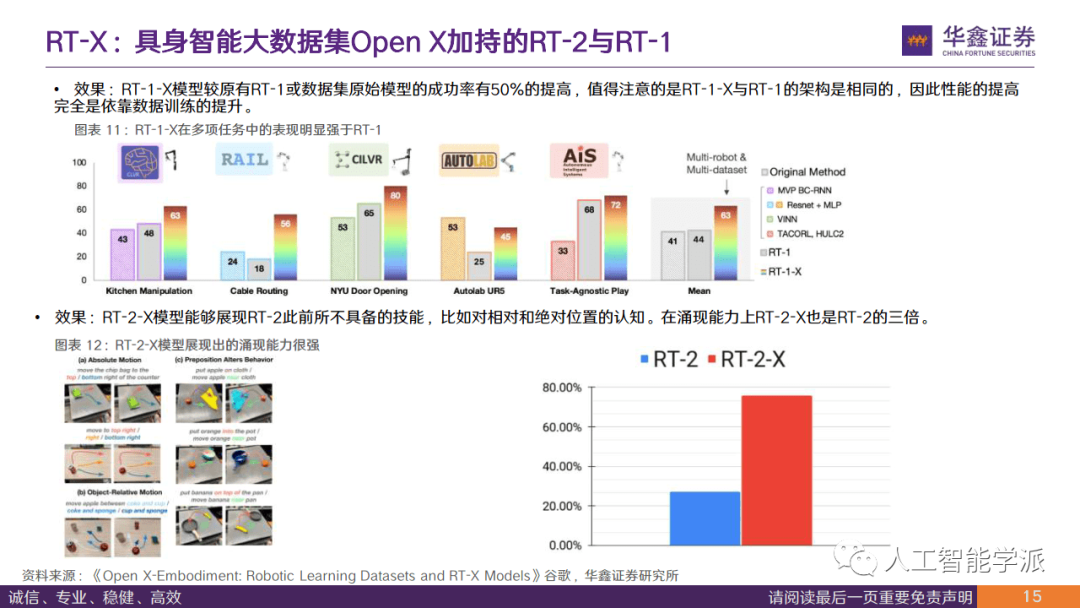
2023人形机器人行业海外科技研究:从谷歌看机器人大模型进展
今天分享的是人形机器人系列深度研究报告:《2023人形机器人行业海外科技研究:从谷歌看机器人大模型进展》。 (报告出品方:华鑫证券) 报告共计:26页 大模型是人形机器人的必备要素 长期来看,人…...

【深度学习笔记】01 数据操作与预处理
01 数据操作与预处理 一、数据操作1.1 基本数据操作1.2 广播机制1.3 索引和切片1.4 节省内存1.5 转换为其他Python对象 二、数据预处理读取数据集处理缺失值转换为张量格式练习 一、数据操作 1.1 基本数据操作 导入torch import torch张量表示一个由数值组成的数组ÿ…...

Python与设计模式--门面模式
8-Python与设计模式–门面模式 一、火警报警器(1) 假设有一组火警报警系统,由三个子元件构成:一个警报器,一个喷水器, 一个自动拨打电话的装置。其抽象如下: class AlarmSensor:def run(self):…...
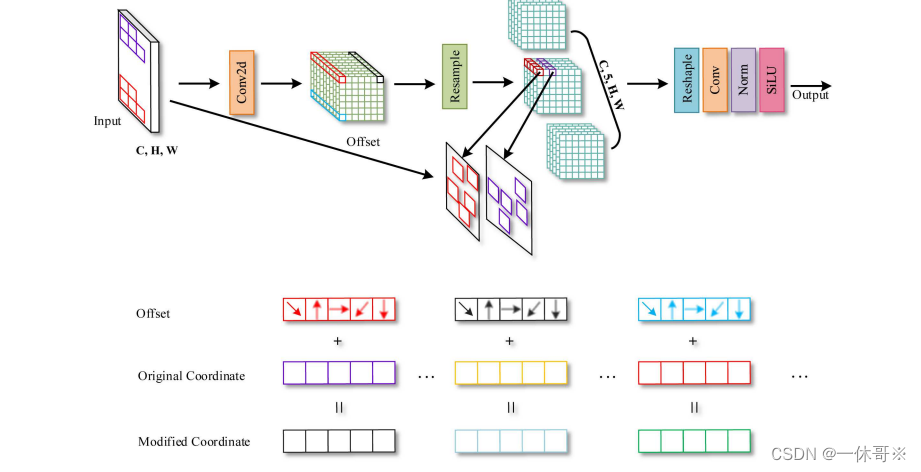
改进YOLOv8 | YOLOv5系列:RFAConv续作,即插即用具有任意采样形状和任意数目参数的卷积核AKCOnv
RFAConv续作,构建具有任意采样形状的卷积AKConv 一、论文yolov5加入的方式论文 源代码 一、论文 基于卷积运算的神经网络在深度学习领域取得了显著的成果,但标准卷积运算存在两个固有缺陷:一方面,卷积运算被限制在一个局部窗口,不能从其他位置捕获信息,并且其采样形状是…...
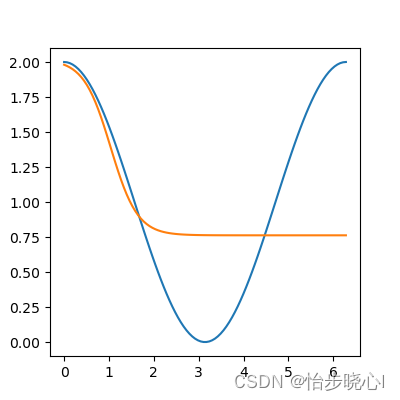
机器学习-激活函数的直观理解
机器学习-激活函数的直观理解 在机器学习中,激活函数(Activation Function)是用于引入非线性特性的一种函数,它在神经网络的每个神经元上被应用。 如果不使用任何的激活函数,那么神经元的响应就是wxb,相当…...
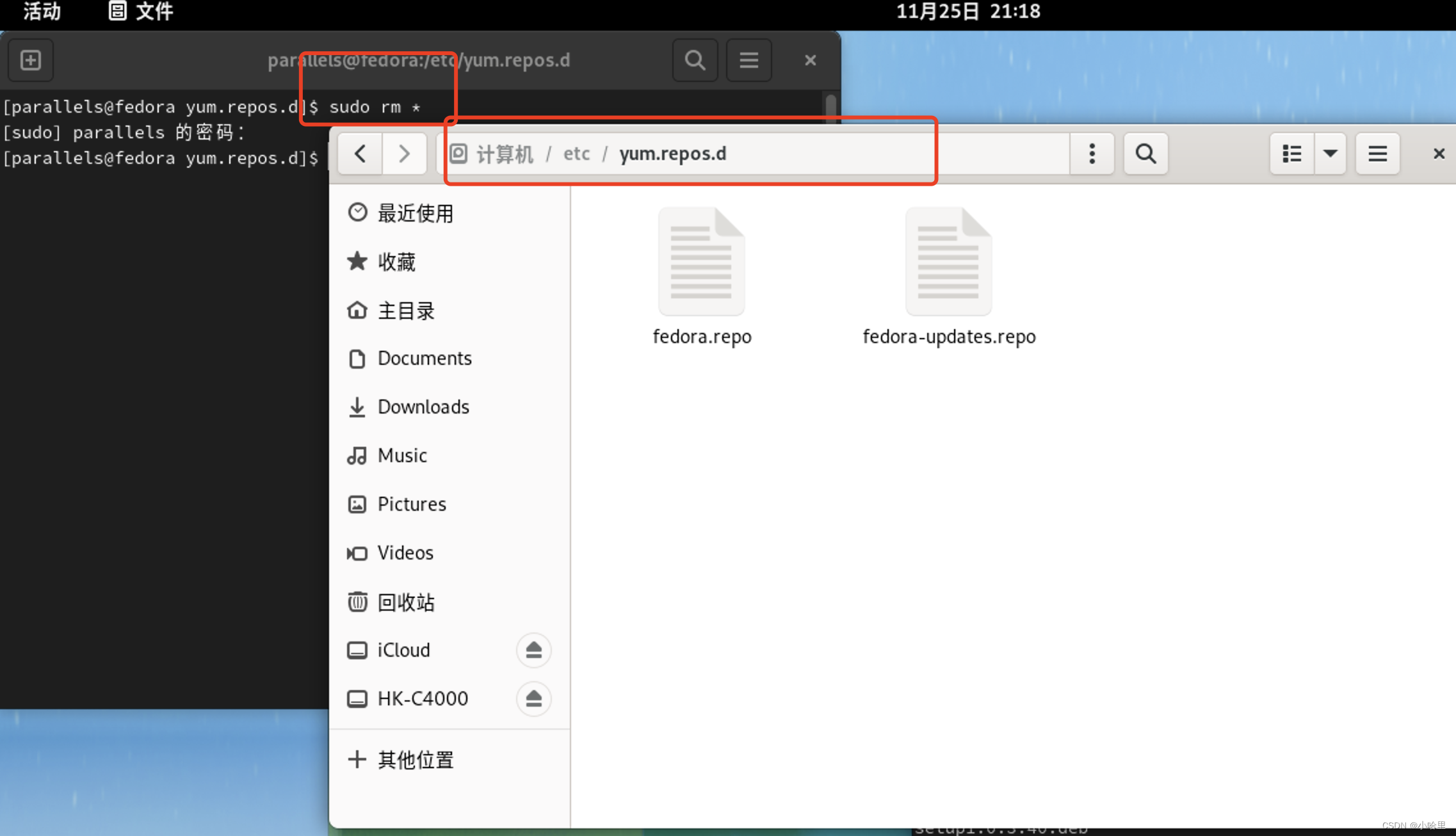
Fedora 36 ARM 镜像源更换与软件安装
1、什么是Fedora Fedora Linux是较具知名度的Linux发行套件之一,由Fedora专案社群开发、红帽公司赞助,目标是建立一套新颖、多功能并且自由的作业系统。 Fedora是商业化的Red Hat Enterprise Linux发行版的上游原始码。 2、Fedora软件安装 64 位 .deb&a…...

多级缓存快速上手
哈喽~大家好,这篇来看看多级缓存。 🥇个人主页:个人主页 🥈 系列专栏:【微服务】 🥉与这篇相关的文章: JAVA进程和线程JAVA进程和线程-CSDN博客Http…...

初始React
<!DOCTYPE html> <html> <head> <meta charset"UTF-8" /> <title>React</title> </head> <body> 了解React <!-- React是一个用于构建web和原生态交互界面的库 相对于传统DOM开发优势:组件化开发…...

2.5 逆矩阵
一、逆矩阵的注释 假设 A A A 是一个方阵,其逆矩阵 A − 1 A^{-1} A−1 与它的大小相同, A − 1 A I A^{-1}AI A−1AI。 A A A 与 A − 1 A^{-1} A−1 会做相反的事情。它们的乘积是单位矩阵 —— 对向量无影响,所以 A − 1 A x x A^{…...
物流实时数仓:数仓搭建(ODS)
系列文章目录 物流实时数仓:采集通道搭建 物流实时数仓:数仓搭建 文章目录 系列文章目录前言一、IDEA环境准备1.pom.xml2.目录创建 二、代码编写1.log4j.properties2.CreateEnvUtil.java3.KafkaUtil.java4.OdsApp.java 三、代码测试总结 前言 现在我们…...

【ARM 嵌入式 编译 Makefile 系列 18 -- Makefile 中的 export 命令详细介绍】
文章目录 Makefile 中的 export 命令详细介绍Makefile 使用 export导出与未导出变量的区别示例:导出变量以供子 Makefile 使用 Makefile 中的 export 命令详细介绍 在 Makefile 中,export 命令用于将变量从 Makefile 导出到由 Makefile 启动的子进程的环…...

【opencv】计算机视觉:停车场车位实时识别
目录 目标 整体流程 背景 详细讲解 目标 我们想要在一个实时的停车场监控视频中,看看要有多少个车以及有多少个空缺车位。然后我们可以标记空的,然后来车之后,实时告诉应该停在那里最方便、最近!!!实现…...
:FFmpeg与SDL环境配置)
播放器开发(三):FFmpeg与SDL环境配置
学习课题:逐步构建开发播放器【QT5 FFmpeg6 SDL2】 环境配置 我这边的是使用macOS;IDE用的是CLion;CMake构建,除了创建项目步骤、CMakeLists文件有区别之外的代码层面不会有太大区别。 配置上只添加一下CMakeLists中FFmpeg和SD…...
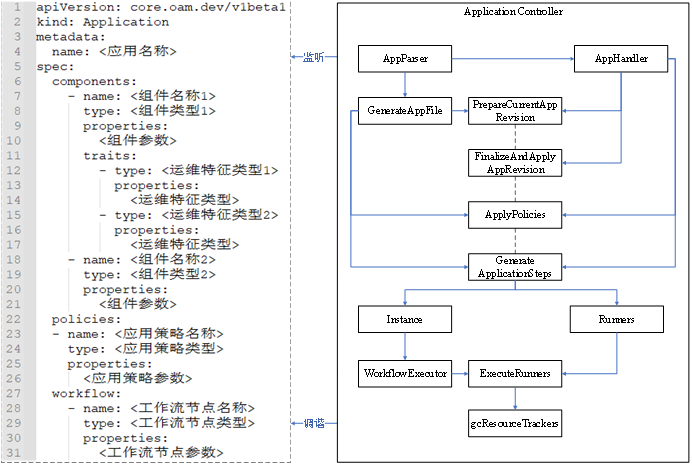
KubeVela核心控制器原理浅析
前言 在学习 KubeVela 的核心控制器之前,我们先简单了解一下 KubeVela 的相关知识。 KubeVela 本身是一个应用交付与管理控制平面,它架在 Kubernetes 集群、云平台等基础设施之上,通过开放应用模型来对组件、云服务、运维能力、交付工作流进…...

迎接“全全闪”时代 XSKY星辰天合发布星海架构和星飞产品
11 月 17 日消息,北京市星辰天合科技股份有限公司(简称:XSKY星辰天合)在北京首钢园举办了主题为“星星之火”的 XSKY 星海全闪架构暨星飞存储发布会。 (图注:XSKY星辰天合 CEO 胥昕) XSKY星辰天…...

[架构相关]基础架构设计原则
基础架构设计原则 文章目录 基础架构设计原则一、可用性(Availability)1.1、引入冗余1.2、负载均衡1.3、故障转移1.4、备份和恢复策略 二、可扩展性(Scalability)2.1 水平扩展2.2 垂直扩展2.3 弹性扩展 三、可靠性(Rel…...

测试在 Oracle 下直接 rm dbf 数据文件并重启数据库
创建一个新的表空间并创建新的用户,指定新表空间为新用户的默认表空间 create tablespace zzw datafile /oradata/cesdb/zzw01.dbf size 10m;zzw用户已经创建过,这里修改其默认表空间 alter user zzw quota unlimited on zzw; alter user zzw default …...

【开源】基于JAVA的计算机机房作业管理系统
项目编号: S 017 ,文末获取源码。 \color{red}{项目编号:S017,文末获取源码。} 项目编号:S017,文末获取源码。 目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 登录注册模块2.2 课程管理模块2.3 课…...

Ubuntu 配置静态 IP
Ubuntu 18 开始可以使用netplan配置网络。配置文件位于/etc/netplan/xxx.yaml中,netplan默认是使用NetworkManager来配置网卡信息的。 修改配置文件: 1、打开文件编辑:sudo vi 01-network-manager-all.yaml原文件内容如下:netwo…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

mac:大模型系列测试
0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何,是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试,是可以跑通文章里面的代码。训练速度也是很快的。 注意…...

Python竞赛环境搭建全攻略
Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型(算法、数据分析、机器学习等)不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...

归并排序:分治思想的高效排序
目录 基本原理 流程图解 实现方法 递归实现 非递归实现 演示过程 时间复杂度 基本原理 归并排序(Merge Sort)是一种基于分治思想的排序算法,由约翰冯诺伊曼在1945年提出。其核心思想包括: 分割(Divide):将待排序数组递归地分成两个子…...
