2.5 逆矩阵
一、逆矩阵的注释
假设 A A A 是一个方阵,其逆矩阵 A − 1 A^{-1} A−1 与它的大小相同, A − 1 A = I A^{-1}A=I A−1A=I。 A A A 与 A − 1 A^{-1} A−1 会做相反的事情。它们的乘积是单位矩阵 —— 对向量无影响,所以 A − 1 A x = x A^{-1}A\boldsymbol x=\boldsymbol x A−1Ax=x,但是 A − 1 A^{-1} A−1 也可能不存在。
矩阵最常见的就是乘一个向量 x \boldsymbol x x, A x = b A\boldsymbol x =\boldsymbol b Ax=b 两边同时乘 A − 1 A^{-1} A−1 得到 A − 1 A x = A − 1 b A^{-1}A\boldsymbol x=A^{-1}\boldsymbol b A−1Ax=A−1b,所以 x = A − 1 b \boldsymbol x=A^{-1}\boldsymbol b x=A−1b。 A − 1 A A^{-1}A A−1A 的乘积就像一个乘一个数再除一个数。如果一个数非零,则必然存在倒数,矩阵会更复杂一些。 A − 1 A^{-1} A−1 称为 A A A 的逆矩阵。
定义 如果存在一个矩阵 A − 1 “逆反” A ,则矩阵 A 可逆: 两边逆反 A − 1 A = I 且 A A − 1 = I ( 2.5.1 ) \pmb{定义}\kern 8pt如果存在一个矩阵\,A^{-1}\,“逆反”\,A,则矩阵\,A\,可逆:\\\pmb{两边逆反}\kern 10ptA^{-1}A=I\,且\,AA^{-1}=I\kern 15pt(2.5.1) 定义如果存在一个矩阵A−1“逆反”A,则矩阵A可逆:两边逆反A−1A=I且AA−1=I(2.5.1)
并不是所有矩阵都有逆矩阵。方阵 A A A 第一个需要讨论的问题是: A A A 是否可逆?这里先不计算 A − 1 A^{-1} A−1,大部分情况下,并不需要计算逆矩阵,下面是逆矩阵的 6 点注释:
Note 1: 矩阵可逆当且仅当消元法可以得到 n n n 个主元(允许行交换)。消元法求解 A x = b A\boldsymbol x=\boldsymbol b Ax=b 时不需要明确使用 A − 1 A^{-1} A−1。
Note 2: 矩阵 A A A 不可能存在两个不同的逆矩阵。假设 B A = I BA=I BA=I 且 A C = I AC=I AC=I,由结合律可得 B = C B=C B=C: B ( A C ) = ( B A ) C 得 B I = I C 或 B = C ( 2.5.2 ) B(AC)=(BA)C\kern 4pt得\kern 4ptBI=IC\kern 4pt或\kern 4ptB=C\kern 15pt(2.5.2) B(AC)=(BA)C得BI=IC或B=C(2.5.2)上式证明了左逆矩阵 B B B(从左边乘)和右逆矩阵 C C C(从右边乘)是相等的。
Note 3: 若矩阵 A A A 可逆, A x = b A\boldsymbol x=\boldsymbol b Ax=b 有唯一解 x = A − 1 b \boldsymbol x=A^{-1}\boldsymbol b x=A−1b:
A − 1 乘 A x = b 得 x = A − 1 A x = A − 1 b A^{-1}\,乘\,A\boldsymbol x=\boldsymbol b\kern 5pt得\kern 5pt\boldsymbol x=A^{-1}A\boldsymbol x=A^{-1}\boldsymbol b A−1乘Ax=b得x=A−1Ax=A−1b
Note 4:(重要)若有一个非零向量 x \boldsymbol x x 使得 A x = 0 A\boldsymbol x=\boldsymbol 0 Ax=0,则 A A A 不可逆。没有这样的矩阵可以将 0 \boldsymbol 0 0 变成 x \boldsymbol x x。
若 A 可逆,则 A x = 0 仅存在零解 x = A − 1 0 = 0 若\,A\,可逆,则\,A\boldsymbol x=\boldsymbol 0\,仅存在零解\,\boldsymbol x=A^{-1}\boldsymbol 0=\boldsymbol 0 若A可逆,则Ax=0仅存在零解x=A−10=0
Note 5: 若 2 × 2 2\times2 2×2 的矩阵 A A A 可逆,当且仅当 a d − b c ≠ 0 ad-bc\neq0 ad−bc=0: 2 × 2 逆矩阵: [ a b c d ] − 1 = 1 a d − b c [ d − b − c a ] ( 2.5.3 ) 2\times2\,逆矩阵:\begin{bmatrix}a&b\\c&d\end{bmatrix}^{-1}=\frac{1}{ad-bc}\begin{bmatrix}\kern 7ptd&-b\\-c&\kern 7pta\end{bmatrix}\kern 15pt(2.5.3) 2×2逆矩阵:[acbd]−1=ad−bc1[d−c−ba](2.5.3) a d − b c ad-bc ad−bc 是 A A A 的行列式,若矩阵的行列式不为零,则矩阵可逆。
Note 6: 若对角线矩阵的对角线元素都不为零,则对角线矩阵可逆:

【例1】 2 × 2 2\times2 2×2 的矩阵 A = [ 1 2 1 2 ] A=\begin{bmatrix}1&2\\1&2\end{bmatrix} A=[1122] 不可逆。因为 a d − b c = 2 − 2 = 0 ad-bc=2-2=0 ad−bc=2−2=0,所以 Note 5 的测试失败。当 x = ( 2 , − 1 ) \boldsymbol x=(2,-1) x=(2,−1) 时 A x = 0 A\boldsymbol x=\boldsymbol 0 Ax=0,所以 Note 3 的测试失败。没有两个主元,所以 Note 1 的测试失败。
消元法会使得矩阵 A A A 的第二行变成零行。
二、AB 乘积的逆矩阵
两个非零数 a a a 和 b b b,它们都有倒数,但它们的和不一定有倒数。例如 a = 3 a=3 a=3, b = − 3 b=-3 b=−3,则 a a a 的倒数是 1 3 \displaystyle\frac{1}{3} 31, b b b 的倒数是 − 1 3 -\displaystyle\frac{1}{3} −31,它们的和 a + b = 0 a+b=0 a+b=0, 0 0 0 没有倒数。但是它们的乘积 a b = − 9 ab=-9 ab=−9 是有倒数的,其倒数是 1 3 × ( − 1 3 ) = − 1 9 \displaystyle\frac{1}{3}\times(-\frac{1}{3})=-\frac{1}{9} 31×(−31)=−91。
对于两个矩阵 A A A 和 B B B 和上面的情况类似,它们的和不一定可逆,但是如果这两个矩阵均可逆,那么它们的乘积 A B AB AB 也可逆。只是 A − 1 A^{-1} A−1 与 B − 1 B^{-1} B−1 需要反序相乘:
如果 A 和 B 均可逆,则 A B 也可逆。 A B 的逆矩阵是: ( A B ) − 1 = B − 1 A − 1 ( 2.5.4 ) 如果\,A\,和\,B\,均可逆,则\,AB\,也可逆。AB\,的逆矩阵是:\\(AB)^{-1}=B^{-1}A^{-1}\kern 18pt(2.5.4) 如果A和B均可逆,则AB也可逆。AB的逆矩阵是:(AB)−1=B−1A−1(2.5.4)
为什么需要反序相乘呢?我们计算 A B AB AB 乘 B − 1 A − 1 B^{-1}A^{-1} B−1A−1,中间会有 B B − 1 = I BB^{-1}=I BB−1=I: A B 的逆矩阵 ( A B ) ( B − 1 A − 1 ) = A I A − 1 = A A − 1 = I AB\,的逆矩阵\kern 20pt(AB)(B^{-1}A^{-1})=AIA^{-1}=AA^{-1}=I AB的逆矩阵(AB)(B−1A−1)=AIA−1=AA−1=I去掉括号,先求 B B − 1 BB^{-1} BB−1。同样的 B − 1 A − 1 B^{-1}A^{-1} B−1A−1 乘 A B AB AB 等于 I I I。
B − 1 A − 1 B^{-1}A^{-1} B−1A−1 说明了一个基本的数学法则,逆矩阵就是逆序。例如先穿袜子再穿鞋子,逆序就是先脱鞋子再脱袜子。三个及三个以上的矩阵同样遵循这样的反序:
反序 ( A B C ) − 1 = C − 1 B − 1 A − 1 ( 2.5.5 ) \pmb{反序}\kern 10pt(ABC)^{-1}=C^{-1}B^{-1}A^{-1}\kern 20pt(2.5.5) 反序(ABC)−1=C−1B−1A−1(2.5.5)
【例2】消元矩阵的逆矩阵。如果 E E E 从行 2 2 2 减去 5 5 5 倍的行 1 1 1,那么 E − 1 E^{-1} E−1 就会将 5 5 5 倍的行 1 1 1 加到行 2 2 2: E 减去 E − 1 加上 E = [ 1 0 0 − 5 1 0 0 0 1 ] , E − 1 = [ 1 0 0 5 1 0 0 0 1 ] \begin{matrix}E\,减去\\E^{-1}\,加上\end{matrix}\kern 10ptE=\begin{bmatrix}\kern 7pt1&0&0\\-5&1&0\\\kern 7pt0&0&1\end{bmatrix},\kern 10ptE^{-1}=\begin{bmatrix}1&0&0\\5&1&0\\0&0&1\end{bmatrix} E减去E−1加上E= 1−50010001 ,E−1= 150010001 E E − 1 EE^{-1} EE−1 将得到单位矩阵 I I I。 E − 1 E E^{-1}E E−1E 也会得到 I I I,它是先加上再减去的 5 5 5 倍的行 1 1 1。如果 A C = I AC=I AC=I,则 C A = I CA=I CA=I。
对于方阵来说,一侧的逆矩阵也是另一侧的逆矩阵。
【例3】假设 F F F 从行 3 3 3 减去 4 4 4 倍的行 2 2 2,则 F − 1 F^{-1} F−1 会将其加回去: F = [ 1 0 0 0 1 0 0 − 4 1 ] , F − 1 = [ 1 0 0 0 1 0 0 4 1 ] F=\begin{bmatrix}1&\kern 7pt0&0\\0&\kern 7pt1&0\\0&-4&1\end{bmatrix},\kern 10ptF^{-1}=\begin{bmatrix}1&0&0\\0&1&0\\0&4&1\end{bmatrix} F= 10001−4001 ,F−1= 100014001 现在用 F F F 乘上例 2 中的 E E E,求出 F E FE FE,同时求出 E − 1 F − 1 E^{-1}F^{-1} E−1F−1。注意 F E FE FE 与 E − 1 F − 1 E^{-1}F^{-1} E−1F−1 的顺序! F E = [ 1 0 0 − 5 1 0 20 − 4 0 ] , E − 1 F − 1 = [ 1 0 0 5 1 0 0 4 1 ] ( 2.5.6 ) FE=\begin{bmatrix}\kern 7pt1&\kern 7pt0&0\\-5&\kern 7pt1&0\\\pmb{20}&-4&0\end{bmatrix},\kern 10ptE^{-1}F^{-1}=\begin{bmatrix}1&0&0\\5&1&0\\0&4&1\end{bmatrix}\kern 15pt(2.5.6) FE= 1−52001−4000 ,E−1F−1= 150014001 (2.5.6)逆矩阵 E − 1 F − 1 E^{-1}F^{-1} E−1F−1 是一个美丽又正确的矩阵, E F EF EF 含有 20 20 20,但是它的逆矩阵却没有。 E E E 从行 2 2 2 减去 5 5 5 倍的行 1 1 1,然后 F F F 从行 3 3 3 中减去 4 4 4 倍新的行 2 2 2 (此时的行 2 2 2 已经被行 1 1 1 改变了)。所以 F E FE FE 会使得行 3 3 3 受到行 1 1 1 的影响。
而按照 E − 1 F − 1 E^{-1}F^{-1} E−1F−1 的顺序,上述影响并没有出现。 F − 1 F^{-1} F−1 将 4 4 4 倍的行 2 2 2 加到行 3 3 3,然后 E − 1 E^{-1} E−1 又将 5 5 5 倍的行 1 1 1 加到行 2 2 2 上,此过程中行 3 3 3 没有再被改变,所以就不再含有 20 20 20。所以 E − 1 F − 1 E^{-1}F^{-1} E−1F−1 不会使行 3 3 3 受到行 1 1 1 的影响。
这也就是为什么会有 A = L U A=LU A=LU,它可以从三角矩阵 U U U 回到 A A A,其乘数将会完美的出现在下三角矩阵 L L L 中。
消元的顺序是先 E 后 F ,逆序是先 F − 1 后 E − 1 E − 1 F − 1 比较快,乘数 5 , 4 落在对角线元素 1 的下方 消元的顺序是先\,E\,后\,F,逆序是先\,F^{-1}\,后\,E^{-1}\\E^{-1}F^{-1}\,比较快,乘数\,5,4\,落在对角线元素\,1\,的下方 消元的顺序是先E后F,逆序是先F−1后E−1E−1F−1比较快,乘数5,4落在对角线元素1的下方
三、高斯-若尔当(Gauss-Jordan)消元法
方程 A x = b A\boldsymbol x=\boldsymbol b Ax=b 的解是 x = A − 1 b \boldsymbol x=A^{-1}\boldsymbol b x=A−1b。使用消元法可以直接求出 x \boldsymbol x x,消元法也可以求出 A − 1 A^{-1} A−1。高斯 - 若尔当的思想就是求解 A A − 1 = I AA^{-1}=I AA−1=I,找到 A − 1 A^{-1} A−1 的每一列。
A A A 乘 A − 1 A^{-1} A−1 的第一列(称为 x 1 \boldsymbol x_1 x1),得到 I I I 的第一列(称为 e 1 \boldsymbol e_1 e1),假设 A A A 的 3 × 3 3\times 3 3×3 的方阵,则方程是 A x 1 = e 1 = ( 1 , 0 , 0 ) A\boldsymbol x_1=\boldsymbol e_1=(1,0,0) Ax1=e1=(1,0,0),同样的还有两个方程。 A A A 乘上 A − 1 A^{-1} A−1 的每一列 x 1 , x 2 , x 3 \boldsymbol x_1,\boldsymbol x_2,\boldsymbol x_3 x1,x2,x3 得到 I I I 的列:
A − 1 的三列 A A − 1 = A [ x 1 x 2 x 3 ] = [ e 1 e 2 e 3 ] = I ( 2.5.7 ) A^{-1}\,的三列\kern 10ptAA^{-1}=A\begin{bmatrix}\boldsymbol x_1&\boldsymbol x_2&\boldsymbol x_3\end{bmatrix}=\begin{bmatrix}\boldsymbol e_1&\boldsymbol e_2&\boldsymbol e_3\end{bmatrix}=I\kern 18pt(2.5.7) A−1的三列AA−1=A[x1x2x3]=[e1e2e3]=I(2.5.7)
要得到 A A A 的逆矩阵,我们需要求解三个方程: A x 1 = e 1 = ( 1 , 0 , 0 ) 、 A x 2 = e 2 = ( 0 , 1 , 0 ) 、 A x 3 = e 3 = ( 0 , 0 , 1 ) A\boldsymbol x_1=\boldsymbol e_1=(1,0,0) 、A\boldsymbol x_2=\boldsymbol e_2=(0,1,0)、A\boldsymbol x_3=\boldsymbol e_3=(0,0,1) Ax1=e1=(1,0,0)、Ax2=e2=(0,1,0)、Ax3=e3=(0,0,1)。高斯 - 若尔当消元法就是用这个方法求逆矩阵 A − 1 A^{-1} A−1。
高斯 - 若尔当消元法是通过同时求解 n n n 个方程来计算 A − 1 A^{-1} A−1。一般来说增广矩阵 [ A b ] \begin{bmatrix}A&\boldsymbol b\end{bmatrix} [Ab] 会多一列 b \boldsymbol b b。当 A A A 是 3 × 3 3\times3 3×3 的矩阵时,会在右侧多 3 3 3 列 e 1 , e 2 , e 3 \boldsymbol e_1,\boldsymbol e_2,\boldsymbol e_3 e1,e2,e3,它们是 I I I 的列,因此增广矩阵就是分块矩阵 [ A I ] \begin{bmatrix}A&I\end{bmatrix} [AI]。下面以矩阵 K K K 为例,它的对角线元素都是 2 2 2, 2 2 2 旁边全是 − 1 -1 −1,其它元素均为 0 0 0: [ K e 1 e 2 e 3 ] = [ 2 − 1 0 1 0 0 − 1 2 − 1 0 1 0 0 − 1 2 0 0 1 ] 开始对 K 进行高斯 − 若尔当消元 → [ 2 − 1 0 1 0 0 0 3 2 − 1 1 2 1 0 0 − 1 2 0 0 1 ] ( 1 2 r o w 1 + r o w 2 ) → [ 2 − 1 0 1 0 0 0 3 2 − 1 1 2 1 0 0 0 4 3 1 3 2 3 1 ] ( 2 3 r o w 2 + r o w 3 ) \begin{bmatrix}K&\boldsymbol e_1&\boldsymbol e_2&\boldsymbol e_3\end{bmatrix}=\begin{bmatrix}\kern 7pt\pmb 2&\pmb{-1}&\kern 7pt\pmb0&1&0&0\\\pmb{-1}&\kern 7pt\pmb2&\pmb{-1}&0&1&0\\\kern 7pt\pmb0&\pmb{-1}&\kern 7pt\pmb2&0&0&1\end{bmatrix}\kern 10pt开始对K进行高斯-若尔当消元\\\kern 13pt\rightarrow\begin{bmatrix}2&-1&\kern 7pt0&1&0&0\\\pmb0&\kern 7pt\displaystyle\pmb{\frac{3}{2}}&\pmb{-1}&\displaystyle\pmb{\frac{1}{2}}&\pmb1&\pmb0\\0&-1&\kern 7pt2&0&0&1\end{bmatrix}\kern 10pt(\frac{1}{2}row1+row2)\\\kern 19pt\rightarrow\begin{bmatrix}2&-1&\kern 7pt0&1&0&0\\0&\kern 7pt\displaystyle\frac{3}{2}&-1&\displaystyle\frac{1}{2}&1&0\\[1.ex]\pmb0&\kern 7pt\pmb0&\kern 7pt\displaystyle\pmb{\frac{4}{3}}&\displaystyle\pmb{\frac{1}{3}}&\displaystyle\pmb{\frac{2}{3}}&\pmb1\end{bmatrix}\kern 10pt(\frac{2}{3}row2+row3) [Ke1e2e3]= 2−10−12−10−12100010001 开始对K进行高斯−若尔当消元→ 200−123−10−121210010001 (21row1+row2)→ 200−12300−134121310132001 (32row2+row3)到这一步只完成了求 K − 1 K^{-1} K−1 的一半,矩阵的前 3 3 3 列是 U U U(上三角),主元 2 , 3 2 , 4 3 2,\displaystyle\frac{3}{2},\frac{4}{3} 2,23,34 在对角线上。高斯在这里会利用回代,而若尔当会继续执行消元!他会一直进行到简化阶梯形式 R = I R=I R=I。通过下面的行继续进行消元,使得主元上方都是零。 ( 第三主元上都为零 ) → [ 2 − 1 0 1 0 0 0 3 2 0 3 4 3 2 3 4 0 0 4 3 1 3 2 3 1 ] ( 3 4 r o w 3 + r o w 2 ) (第三主元上都为零)\rightarrow\begin{bmatrix}2&-1&0&1&0&0\\[1.ex]\pmb0&\kern 7pt\displaystyle\pmb{\frac{3}{2}}&\pmb0&\displaystyle\pmb{\frac{3}{4}}&\displaystyle\pmb{\frac{3}{2}}&\displaystyle\pmb{\frac{3}{4}}\\[2.ex]0&\kern 7pt0&\displaystyle\frac{4}{3}&\displaystyle\frac{1}{3}&\displaystyle\frac{2}{3}&1\end{bmatrix}\kern 10pt(\frac{3}{4}row3+row2) (第三主元上都为零)→ 200−1230003414331023320431 (43row3+row2) ( 第二主元上都为零 ) → [ 2 0 0 3 2 1 1 2 0 3 2 0 3 4 3 2 3 4 0 0 4 3 1 3 2 3 1 ] ( 2 3 r o w 2 + r o w 1 ) (第二主元上都为零)\rightarrow\begin{bmatrix}\pmb2&\pmb0&\pmb0&\displaystyle\pmb{\frac{3}{2}}&\pmb1&\displaystyle\pmb{\frac{1}{2}}\\[1.5ex]0&\displaystyle\frac{3}{2}&0&\displaystyle\frac{3}{4}&\displaystyle\frac{3}{2}&\displaystyle\frac{3}{4}\\[1.5ex]0&0&\displaystyle\frac{4}{3}&\displaystyle\frac{1}{3}&\displaystyle\frac{2}{3}&1\end{bmatrix}\kern 10pt(\frac{2}{3}row2+row1) (第二主元上都为零)→ 200023000342343311233221431 (32row2+row1)高斯 - 若尔当的最后一步是将每行除以改行的主元,使新的主元全部为 1 1 1。
因为 K K K 是可逆的,所以矩阵 [ I K − 1 ] \begin{bmatrix}I&K^{-1}\end{bmatrix} [IK−1] 的左半部分是 I I I,右半部分就是 K − 1 K^{-1} K−1: ( 除以 2 ) ( 除以 3 2 ) ( 除以 4 3 ) [ 1 0 0 3 4 1 2 1 4 0 1 0 1 2 1 1 2 0 0 1 1 4 1 2 3 4 ] = [ I x 1 x 2 x 3 ] = [ I K − 1 ] \begin{matrix}(除以\,2)\\[1.5ex](除以\displaystyle\frac{3}{2})\\[1.5ex](除以\displaystyle\frac{4}{3})\end{matrix}\kern 8pt\begin{bmatrix}\pmb1&0&0&\displaystyle\pmb{\frac{3}{4}}&\displaystyle\pmb{\frac{1}{2}}&\displaystyle\pmb{\frac{1}{4}}\\[1.5ex]0&\pmb1&0&\displaystyle\pmb{\frac{1}{2}}&\pmb1&\displaystyle\pmb{\frac{1}{2}}\\[1.5ex]0&0&\pmb1&\displaystyle\pmb{\frac{1}{4}}&\displaystyle\pmb{\frac{1}{2}}&\displaystyle\pmb{\frac{3}{4}}\end{bmatrix}=\begin{bmatrix}I&\boldsymbol x_1&\boldsymbol x_2&\boldsymbol x_3\end{bmatrix}=\begin{bmatrix}I&K^{-1}\end{bmatrix} (除以2)(除以23)(除以34) 10001000143214121121412143 =[Ix1x2x3]=[IK−1]从 3 × 6 3\times6 3×6 的矩阵 [ K I ] \begin{bmatrix}K&I\end{bmatrix} [KI] 开始,以 [ I K − 1 ] \begin{bmatrix}I&K^{-1}\end{bmatrix} [IK−1] 结束。对于任意的可逆矩阵 A A A,应用高斯 - 若尔当消元法:
Gauss-Jordan A − 1 乘 [ A I ] 得到 [ I A − 1 ] \textrm{Gauss-Jordan}\kern15ptA^{-1}乘\begin{bmatrix}A&I\end{bmatrix}得到\begin{bmatrix}I&A^{-1}\end{bmatrix} Gauss-JordanA−1乘[AI]得到[IA−1]
消元步骤在将 A A A 变为 I I I 过程中会得到逆矩阵。对于大型矩阵,我们可能并不想要 A − 1 A^{-1} A−1,但是对于小型矩阵,得到逆矩阵可能会很重要。下面是关于 K − 1 K^{-1} K−1 的三条观察结果:
- K K K 是关于主对角线对称, K − 1 K^{-1} K−1 也是对称的。
- K K K 是三对角(tridiagonal)矩阵(只有 3 3 3 个非零对角线),但是 K − 1 K^{-1} K−1 是一个没有 0 0 0 的稠密(dense)矩阵。这也是另一个不常计算逆矩阵的原因。带状(band)矩阵通常都是稠密矩阵。
- 主元的乘积是 2 ( 3 2 ) ( 4 3 ) = 4 2(\displaystyle\frac{3}{2})(\frac{4}{3})=4 2(23)(34)=4。 4 4 4 就是 K K K 的行列式。 K − 1 与 K 的行列式做除数有关 K − 1 = 1 4 [ 3 2 1 2 4 2 1 2 3 ] ( 2.5.8 ) K^{-1}与K的行列式做除数有关\kern 15ptK^{-1}=\frac{1}{4}\begin{bmatrix}3&2&1\\2&4&2\\1&2&3\end{bmatrix}\kern 14pt(2.5.8) K−1与K的行列式做除数有关K−1=41 321242123 (2.5.8)这就是可逆矩阵的行列式不为零的原因:因为要除以行列式。
【例4】使用高斯 - 若尔当消元法求 A − 1 A^{-1} A−1, A = [ 2 3 4 7 ] A=\begin{bmatrix}2&3\\4&7\end{bmatrix} A=[2437]。
解: [ A I ] = [ 2 3 1 0 4 7 0 1 ] → [ 2 3 1 0 0 1 − 2 1 ] ( 这是 [ U L − 1 ] ) \begin{bmatrix}A&I\end{bmatrix}=\begin{bmatrix}\pmb2&\pmb3&1&0\\\pmb4&\pmb7&0&1\end{bmatrix}\rightarrow\begin{bmatrix}2&3&\kern 7pt1&0\\\pmb0&\pmb1&\pmb{-2}&\pmb1\end{bmatrix}\kern 38pt(这是\begin{bmatrix}U&L^{-1}\end{bmatrix}) [AI]=[24371001]→[20311−201](这是[UL−1]) → [ 2 0 7 − 3 0 1 − 2 1 ] → [ 1 0 7 2 − 3 2 0 1 − 2 1 ] ( 这是 [ I A − 1 ] ) \kern 32pt\rightarrow\begin{bmatrix}\pmb2&\pmb0&\kern 7pt\pmb7&\pmb{-3}\\0&1&-2&1\end{bmatrix}\rightarrow\begin{bmatrix}1&0&\kern 7pt\displaystyle\pmb{\frac{7}{2}}&\displaystyle\pmb{-\frac{3}{2}}\\0&1&\pmb{-2}&\kern 7pt\pmb1\end{bmatrix}\kern 10pt(这是\begin{bmatrix}I&A^{-1}\end{bmatrix}) →[20017−2−31]→[100127−2−231](这是[IA−1])【例5】如果 A A A 是可逆的上三角矩阵,那么 A − 1 A^{-1} A−1 也是。从 A A − 1 = I AA^{-1}=I AA−1=I 开始。
- A A A 乘 A − 1 A^{-1} A−1 的第 j j j 列等于 I I I 的第 j j j 列,该列后面有 n − j n-j n−j 个零。
- 使用回代可以得到 A − 1 A^{-1} A−1 的第 j j j 列后面有 n − j n-j n−j 个零。
- 将这些列 [ ∗ ⋯ ∗ ⋯ ∗ ] T \begin{bmatrix}*\cdots*\cdots*\end{bmatrix}^T [∗⋯∗⋯∗]T 都放进 A − 1 A^{-1} A−1 中,就可得到 A − 1 A^{-1} A−1 是也是一个上三角矩阵。
A − 1 = [ 1 − 1 0 0 1 − 1 0 0 1 ] − 1 = [ 1 1 1 0 1 1 0 0 1 ] 列 j = 1 和 2 后面有 3 − j = 2 和 1 个 0 A^{-1}=\begin{bmatrix}1&-1&\kern 7pt0\\\pmb0&\kern 7pt1&-1\\\pmb0&\kern 7pt\pmb0&\kern 7pt1\end{bmatrix}^{-1}=\begin{bmatrix}1&1&1\\\pmb0&1&1\\\pmb0&\pmb0&1\end{bmatrix}\kern 5pt\begin{matrix}列\,j=1\,和\,2\,后面有\\3-j=2\,和\,1个\,0\end{matrix} A−1= 100−1100−11 −1= 100110111 列j=1和2后面有3−j=2和1个0在 MATLAB 中使用 X = inv(A) 求 A A A 的逆矩阵,该函数是利用 rref(reduced row echelon form)将矩阵简化为行阶梯形式
I = eye(n); % 定义 n×n 的单位矩阵
R = rref([A I]); % 对增广矩阵 [A I] 执行消元法
X = R(:, n+1:n+n); % 取出 R 后面的 n 列 X 就是 A 的逆矩阵

这里的 A A A 必须可逆,否则消元法不能将 A A A 变成 I I I( R R R 的左半部分)。
从高斯 - 若尔当消元法可以看出,要计算一个 A − 1 A^{-1} A−1 需要大量的计算,若有 n n n 列,则需要 n n n 个方程,但是每个方程都有左侧的 A A A 相关(这是工作量最大的地方), A − 1 A^{-1} A−1 整体需要 n 3 n^3 n3 次乘法和减法,求解一个 A x = b A\boldsymbol x=\boldsymbol b Ax=b 需要 n 3 / 3 n^3/3 n3/3 次乘法和加法。
不用 A − 1 A^{-1} A−1 去求解 A x = b A\boldsymbol x=\boldsymbol b Ax=b,我们用一个列 b \boldsymbol b b 去求一个列 x \boldsymbol x x。
四、奇异与可逆的对比
什么样的矩阵可逆?若 A A A 存在一整组主元(允许行交换),则 A − 1 A^{-1} A−1 存在。 我们可以使用高斯 - 若尔当消元法来证明:
- 有 n n n 个主元时,消元法求解所有的方程 A x i = e i A\boldsymbol x_i=\boldsymbol e_i Axi=ei,列 x i \boldsymbol x_i xi 进入 A − 1 A^{-1} A−1,则 A A − 1 = I AA^{-1}=I AA−1=I 并且 A − 1 A^{-1} A−1 至少是右逆矩阵。
- 消元法是用一系列矩阵 E ′ s E's E′s, P ′ s P's P′s 和 D − 1 D^{-1} D−1 的乘法: 左逆矩阵 C C A = ( D − 1 ⋯ E ⋯ P ⋯ E ) A = I ( 2.5.9 ) 左逆矩阵\,C\kern 15ptCA=(D^{-1}\cdots E\cdots P\cdots E)A=I\kern 10pt(2.5.9) 左逆矩阵CCA=(D−1⋯E⋯P⋯E)A=I(2.5.9)
D − 1 D^{-1} D−1 是除以主元,矩阵 E E E 使得主元上方和下方的元素变为 0 0 0, P P P 是在需要时进行行交换。式(9)中这些矩阵的乘积就是 A A A 的左逆矩阵。使用 n n n 个主元得到 A − 1 A = I A^{-1}A=I A−1A=I。
由 Note2 知:左逆矩阵等于右逆矩阵,所以有一整组主元的方阵两边都存在逆矩阵,且相等。
下面证明若 A C = I AC=I AC=I,则 A A A 一定有 n n n 个主元。
- 如果 A A A 没有 n n n 个主元,则消元法会得到一个零行。
- 这些消元步骤可以用可逆矩阵 M M M 实现,所以 M A MA MA 也有一个零行。
- 因为 A C = I AC=I AC=I,所以 M A C = M MAC=M MAC=M, M A MA MA 的零行乘 C C C 也会得到一个零行。
- 可逆矩阵 M M M 不可能存在零行!所以若 A C = I AC=I AC=I,则 A A A 一定有 n n n 个主元。 C C C 就是 A − 1 A^{-1} A−1。
消元法提供了方阵可逆的完整测试。当 A A A 有 n n n 个主元时, A − 1 A^{-1} A−1 一定存在(可通过高斯 - 若尔当消元法找到):
如果 A C = I ,则 C A = I 且 C = A − 1 ( 2.5.10 ) 如果\, AC=I,则\,CA=I\,且\,C=A^{-1}\kern 15pt(2.5.10) 如果AC=I,则CA=I且C=A−1(2.5.10)
【例6】如果 L L L 是下三角矩阵且对角线元素都是 1 1 1,则 L − 1 L^{-1} L−1 也是。
使用高斯 - 若尔当消元法从 E 32 , E 31 , E 21 E_{32},E_{31},E_{21} E32,E31,E21 创建 L − 1 L^{-1} L−1。 [ 1 0 0 1 0 0 3 1 0 0 1 0 4 5 1 0 0 1 ] = [ L I ] → [ 1 0 0 1 0 0 0 1 0 − 3 1 0 0 5 1 − 4 0 1 ] 逆矩阵 仍是三角形 → [ 1 0 0 1 0 0 0 1 0 − 3 1 0 0 0 1 11 − 5 1 ] = [ I L − 1 ] \kern 50pt\begin{bmatrix}\pmb1&\pmb0&\pmb0&1&0&0\\\pmb3&\pmb1&\pmb0&0&1&0\\\pmb4&\pmb5&\pmb1&0&0&1\end{bmatrix}=\begin{bmatrix}L&I\end{bmatrix}\\\rightarrow\begin{bmatrix}1&0&0&\kern 7pt1&0&0\\0&1&0&-3&1&0\\0&5&1&-4&0&1\end{bmatrix}\\\begin{matrix}逆矩阵\\仍是三角形\end{matrix}\kern 10pt\rightarrow\begin{bmatrix}1&0&0&\kern 7pt\pmb1&\kern 7pt\pmb0&\pmb0\\0&1&0&\pmb{-3}&\kern 7pt\pmb1&\pmb0\\0&0&1&\kern 4pt\pmb{11}&\pmb{-5}&\pmb1\end{bmatrix}=\begin{bmatrix}I&L^{-1}\end{bmatrix} 134015001100010001 =[LI]→ 1000150011−3−4010001 逆矩阵仍是三角形→ 1000100011−31101−5001 =[IL−1]
五、分辨逆矩阵
正常情况下,若要判断一个矩阵是否可逆,需要做很多工作。通常是使用消元法去找它是否存在一整组的非零主元。但是有些矩阵可以很快速的判断出它是否可逆,例如它是一个严格对角线优势(diagonally dominant)矩阵。
严格对角线优势矩阵是可逆的。这种矩阵的对角线元素 a i i a_{ii} aii 的绝对值比改行其它所有元素绝对值的和还要大,对于每一行都有: ∣ a i i ∣ > ∑ j ≠ i ∣ a i j ∣ ,即 ∣ a i i ∣ = ∣ a i 1 ∣ + ⋯ + ( 跳过 ∣ a i i ∣ ) + ⋯ ∣ a i n ∣ ( 2.5.11 ) |a_{ii}|>\sum_{j\neq i}|a_{ij}|,即\,|a_{ii}|=|a_{i1}|+\cdots+(跳过|a_{ii}|)+\cdots |a_{in}|\kern 10pt(2.5.11) ∣aii∣>j=i∑∣aij∣,即∣aii∣=∣ai1∣+⋯+(跳过∣aii∣)+⋯∣ain∣(2.5.11)下面三个矩阵 A A A 是严格对角线优势矩阵 ( 3 > 2 ) (3>2) (3>2), B B B 不是(但仍然可逆), C C C 是奇异矩阵。 A = [ 3 1 1 1 3 1 1 1 3 ] , B = [ 2 1 1 1 2 1 1 1 3 ] , C = [ 1 1 1 1 1 1 1 1 3 ] A=\begin{bmatrix}3&1&1\\1&3&1\\1&1&3\end{bmatrix},\kern 10ptB=\begin{bmatrix}2&1&1\\1&2&1\\1&1&3\end{bmatrix},\kern 10ptC=\begin{bmatrix}1&1&1\\1&1&1\\1&1&3\end{bmatrix} A= 311131113 ,B= 211121113 ,C= 111111113 原因: 对于任意的非零向量 x \boldsymbol x x,假设它最大的分量是 ∣ x i ∣ |x_i| ∣xi∣。那么不可能有 A x = 0 A\boldsymbol x=\boldsymbol 0 Ax=0。此时选择 A A A 的行 i i i,则若要 A x A\boldsymbol x Ax 的行 i i i 为 0 0 0,则有: a i 1 x 1 + ⋯ a i i x i + ⋯ + a i n x n = 0 a_{i1}x_1+\cdots a_{ii}x_i+\cdots+a_{in}x_n=0 ai1x1+⋯aiixi+⋯+ainxn=0而上述不可能为零。因为 ∣ a i i x i ∣ |a_{ii}x_i| ∣aiixi∣ 比其他所有的和还要大。 所有的 ∣ x j ∣ < ∣ x i ∣ ∑ j ≠ i ∣ a i j x j ∣ ≤ ∑ j ≠ i ∣ a i j ∣ ∣ x j ∣ < ∣ a i i ∣ ∣ x i ∣ 因为 a i i 占优势 所有的|x_j|<|x_i|\kern 10pt\sum_{j\neq i}|a_{ij}x_j|\leq\sum_{j\neq i}|a_{ij}||x_j|<|a_{ii}||x_i|\kern 10pt因为a_{ii}占优势 所有的∣xj∣<∣xi∣j=i∑∣aijxj∣≤j=i∑∣aij∣∣xj∣<∣aii∣∣xi∣因为aii占优势因此只有当 x = 0 \boldsymbol x=\boldsymbol 0 x=0 时 A x = 0 A\boldsymbol x=\boldsymbol 0 Ax=0 才成立,所有 A A A 可逆。需要注意的是,若不是对角线优势矩阵也不一定不可逆,例如 B B B 不是对角线优势矩阵,它仍然可逆。
六、主要内容总结
- 逆矩阵有 A A − 1 = I AA^{-1}=I AA−1=I 且 A − 1 A = I A^{-1}A=I A−1A=I。
- A A A 可逆当且仅当它有 n n n 个主元(允许行交换)。
- (重要)。如果存在非零向量 x \boldsymbol x x 使得 A x = 0 A\boldsymbol x=\boldsymbol 0 Ax=0,则 A A A 不可逆。
- A B AB AB 的逆矩阵是反序乘积 B − 1 A − 1 B^{-1}A^{-1} B−1A−1, ( A B C ) − 1 = C − 1 B − 1 A − 1 (ABC)^{-1}=C^{-1}B^{-1}A^{-1} (ABC)−1=C−1B−1A−1。
- 高斯 - 若尔当消元法求解 A A − 1 = I AA^{-1}=I AA−1=I 可以得到 A − 1 A^{-1} A−1 的 n n n 个列。增广矩阵 [ A I ] \begin{bmatrix}A&I\end{bmatrix} [AI] 使用行简化得到 [ I A − 1 ] \begin{bmatrix}I&A^{-1}\end{bmatrix} [IA−1]。
- 严格对角线优势矩阵是可逆的。每个 ∣ a i i ∣ |a_{ii}| ∣aii∣ 在它所在的行站主导地位。
七、例题
【例7】三角形差分矩阵 A A A 的逆矩阵是三角形求和矩阵 S S S: [ A I ] = [ 1 0 0 1 0 0 − 1 1 0 0 1 0 0 − 1 1 0 0 1 ] → [ 1 0 0 1 0 0 0 1 0 1 1 0 0 − 1 1 0 0 1 ] → [ 1 0 0 1 0 0 0 1 0 1 1 0 0 0 1 1 1 1 ] = [ I A − 1 ] = [ I 求和矩阵 ] \begin{bmatrix}A&I\end{bmatrix}=\left[\begin{array}{ccc|c}\kern 7pt1&\kern 7pt0&0&1&0&0\\-1&\kern 7pt1&0&0&1&0\\\kern 7pt0&-1&1&0&0&1\end{array}\right]\rightarrow\left[\begin{array}{ccc|c}1&\kern 7pt0&0&1&0&0\\0&\kern 7pt1&0&1&1&0\\0&-1&1&0&0&1\end{array}\right]\kern 18pt\\\rightarrow\left[\begin{array}{ccc|c}1&0&0&1&0&0\\0&1&0&1&1&0\\0&0&1&1&1&1\end{array}\right]=\begin{bmatrix}I&A^{-1}\end{bmatrix}=\begin{bmatrix}I&求和矩阵\end{bmatrix} [AI]= 1−1001−1001100010001 → 10001−1001110010001 → 100010001111011001 =[IA−1]=[I求和矩阵]如果将 a 13 a_{13} a13 改为 − 1 -1 −1,则 A A A 所有的行加起来都是 0 0 0,方程 A x = 0 A\boldsymbol x=\boldsymbol 0 Ax=0 将会存在非零解 ( 1 , 1 , 1 ) (1,1,1) (1,1,1),所以新的矩阵 A A A 将不可逆。
【例8】下列矩阵有 3 3 3 个可逆, 3 3 3 个不可逆。如果可逆,找出其逆矩阵,若不可逆,说明原因(零行列式,主元太少, A x = 0 A\boldsymbol x=\boldsymbol 0 Ax=0 有非零解)。下列矩阵按顺序为 A , B , C , D , S , E A,B,C,D,S,E A,B,C,D,S,E。
[ 4 3 8 6 ] [ 4 3 8 7 ] [ 6 6 6 0 ] [ 6 6 6 6 ] [ 1 0 0 1 1 0 1 1 1 ] [ 1 1 1 1 1 0 1 1 1 ] \begin{bmatrix}4&3\\8&6\end{bmatrix}\kern 10pt\begin{bmatrix}4&3\\8&7\end{bmatrix}\kern 10pt\begin{bmatrix}6&6\\6&0\end{bmatrix}\kern 10pt\begin{bmatrix}6&6\\6&6\end{bmatrix}\kern 10pt\begin{bmatrix}1&0&0\\1&1&0\\1&1&1\end{bmatrix}\kern 10pt\begin{bmatrix}1&1&1\\1&1&0\\1&1&1\end{bmatrix} [4836][4837][6660][6666] 111011001 111111101
解: B − 1 = 1 4 [ 7 − 3 − 8 4 ] C − 1 = 1 36 [ 0 6 6 − 6 ] S − 1 = [ 1 0 0 − 1 1 0 1 − 1 1 ] B^{-1}=\frac{1}{4}\begin{bmatrix}7&-3\\-8&4\end{bmatrix}\kern 10ptC^{-1}=\frac{1}{36}\begin{bmatrix}0&6\\6&-6\end{bmatrix}\kern 10ptS^{-1}=\begin{bmatrix}\kern 7pt1&\kern 7pt0&0\\-1&\kern 7pt1&0\\\kern 7pt1&-1&1\end{bmatrix} B−1=41[7−8−34]C−1=361[066−6]S−1= 1−1101−1001 A A A 不可逆,因为其行列式为 4 ⋅ 6 − 3 ⋅ 8 = 24 − 24 = 0 4\cdot6-3\cdot8=24-24=0 4⋅6−3⋅8=24−24=0。 D D D 不可逆,因为它仅有一个主元;行 2 2 2 减去行 1 1 1 变成了零行。 E E E 有两个相等的列,或者说 E x = 0 E\boldsymbol x=\boldsymbol 0 Ex=0 有非零解 ( − 1 , 1 , 0 ) (-1,1,0) (−1,1,0)。
不可逆的矩阵均可使用这三个原因。
【例9】使用高斯 - 若尔当消元法求三角帕斯卡(Pascal)矩阵。帕斯卡三角–每个元素加上其左侧元素等于它下面的元素。矩阵 L L L 的元素是二项式系数。下一行将会是 1 , 4 , 6 , 4 , 1 1,4,6,4,1 1,4,6,4,1。 三角帕斯卡矩阵 L = [ 1 0 0 0 1 1 0 0 1 2 1 0 1 3 3 1 ] = abs(pascal(4,1)) 三角帕斯卡矩阵\kern 10ptL=\begin{bmatrix}\pmb1&0&0&0\\\pmb1&\pmb1&0&0\\\pmb1&\pmb2&\pmb1&0\\\pmb1&\pmb3&\pmb3&\pmb1\end{bmatrix}=\textrm{abs(pascal(4,1))} 三角帕斯卡矩阵L= 1111012300130001 =abs(pascal(4,1))解: 高斯 - 若尔当消元法从 [ L I ] \begin{bmatrix}L&I\end{bmatrix} [LI] 开始,通过减去行 1 1 1 使得第一主元下方都为 0 0 0 [ L I ] = [ 1 0 0 0 1 0 0 0 1 1 0 0 0 1 0 0 1 2 1 0 0 0 1 0 1 3 3 1 0 0 0 1 ] → [ 1 0 0 0 1 0 0 0 0 1 0 0 − 1 1 0 0 0 2 1 0 − 1 0 1 0 0 3 3 1 − 1 0 0 1 ] \begin{bmatrix}L&I\end{bmatrix}=\left[\begin{array}{cccc|}\pmb1&0&0&0&1&0&0&0\\\pmb1&\pmb1&0&0&0&1&0&0\\\pmb1&\pmb2&\pmb1&0&0&0&1&0\\\pmb1&\pmb3&\pmb3&\pmb1&0&0&0&1\end{array}\right]\rightarrow\left[\begin{array}{cccc|}1&0&0&0&\kern 7pt1&0&0&0\\\pmb0&1&0&0&\pmb{-1}&1&0&0\\\pmb0&2&1&0&\pmb{-1}&0&1&0\\\pmb0&3&3&1&\pmb{-1}&0&0&1\end{array}\right] [LI]= 11110123001300011000010000100001 → 10000123001300011−1−1−1010000100001 下一步会使第二主元下方都变为 0 0 0,乘数是 2 2 2 和 3 3 3。然后使第三主元下方变为 0 0 0,乘数是 3 3 3 → [ 1 0 0 0 1 0 0 0 0 1 0 0 − 1 1 0 0 0 0 1 0 1 − 2 1 0 0 0 3 1 2 − 3 0 1 ] → [ 1 0 0 0 1 0 0 0 0 1 0 0 − 1 1 0 0 0 0 1 0 1 − 2 1 0 0 0 0 1 − 1 3 − 3 1 ] = [ I L − 1 ] \rightarrow\left[\begin{array}{cccc|}1&0&0&0&\kern 7pt1&\kern 7pt0&0&0\\0&1&0&0&-1&\kern 7pt1&0&0\\0&\pmb0&1&0&\kern 7pt\pmb1&\pmb{-2}&1&0\\0&\pmb0&3&1&\kern 7pt\pmb2&\pmb{-3}&0&1\end{array}\right]\rightarrow\left[\begin{array}{cccc|}1&0&0&0&\kern 7pt\pmb1&\kern 7pt0&\kern 7pt0&0\\0&1&0&0&\pmb{-1}&\kern 7pt\pmb1&\kern 7pt0&0\\0&0&1&0&\kern 7pt\pmb1&\pmb{-2}&\kern 7pt\pmb1&0\\0&0&\pmb0&1&\pmb{-1}&\kern 7pt\pmb3&\pmb{-3}&\pmb1\end{array}\right]=\begin{bmatrix}I&L^{-1}\end{bmatrix} → 10000100001300011−11201−2−300100001 → 10000100001000011−11−101−23001−30001 =[IL−1]由于所有的主元都是 1 1 1,所有没有必要再让每行除以主元得到 I I I。逆矩阵 L − 1 L^{-1} L−1 和 L L L 很像,只是奇对角线处是负号。
同样可以扩展到 n × n n\times n n×n 的帕斯卡矩阵, L − 1 L^{-1} L−1 的对角线交替符号。
相关文章:

2.5 逆矩阵
一、逆矩阵的注释 假设 A A A 是一个方阵,其逆矩阵 A − 1 A^{-1} A−1 与它的大小相同, A − 1 A I A^{-1}AI A−1AI。 A A A 与 A − 1 A^{-1} A−1 会做相反的事情。它们的乘积是单位矩阵 —— 对向量无影响,所以 A − 1 A x x A^{…...
物流实时数仓:数仓搭建(ODS)
系列文章目录 物流实时数仓:采集通道搭建 物流实时数仓:数仓搭建 文章目录 系列文章目录前言一、IDEA环境准备1.pom.xml2.目录创建 二、代码编写1.log4j.properties2.CreateEnvUtil.java3.KafkaUtil.java4.OdsApp.java 三、代码测试总结 前言 现在我们…...

【ARM 嵌入式 编译 Makefile 系列 18 -- Makefile 中的 export 命令详细介绍】
文章目录 Makefile 中的 export 命令详细介绍Makefile 使用 export导出与未导出变量的区别示例:导出变量以供子 Makefile 使用 Makefile 中的 export 命令详细介绍 在 Makefile 中,export 命令用于将变量从 Makefile 导出到由 Makefile 启动的子进程的环…...

【opencv】计算机视觉:停车场车位实时识别
目录 目标 整体流程 背景 详细讲解 目标 我们想要在一个实时的停车场监控视频中,看看要有多少个车以及有多少个空缺车位。然后我们可以标记空的,然后来车之后,实时告诉应该停在那里最方便、最近!!!实现…...
:FFmpeg与SDL环境配置)
播放器开发(三):FFmpeg与SDL环境配置
学习课题:逐步构建开发播放器【QT5 FFmpeg6 SDL2】 环境配置 我这边的是使用macOS;IDE用的是CLion;CMake构建,除了创建项目步骤、CMakeLists文件有区别之外的代码层面不会有太大区别。 配置上只添加一下CMakeLists中FFmpeg和SD…...
KubeVela核心控制器原理浅析
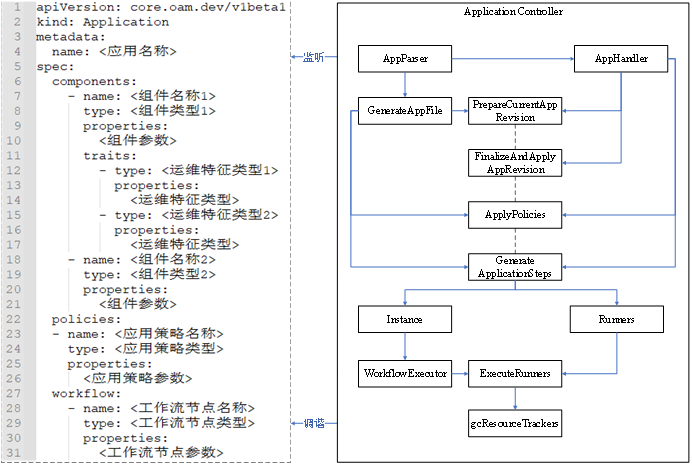
前言 在学习 KubeVela 的核心控制器之前,我们先简单了解一下 KubeVela 的相关知识。 KubeVela 本身是一个应用交付与管理控制平面,它架在 Kubernetes 集群、云平台等基础设施之上,通过开放应用模型来对组件、云服务、运维能力、交付工作流进…...

迎接“全全闪”时代 XSKY星辰天合发布星海架构和星飞产品
11 月 17 日消息,北京市星辰天合科技股份有限公司(简称:XSKY星辰天合)在北京首钢园举办了主题为“星星之火”的 XSKY 星海全闪架构暨星飞存储发布会。 (图注:XSKY星辰天合 CEO 胥昕) XSKY星辰天…...

[架构相关]基础架构设计原则
基础架构设计原则 文章目录 基础架构设计原则一、可用性(Availability)1.1、引入冗余1.2、负载均衡1.3、故障转移1.4、备份和恢复策略 二、可扩展性(Scalability)2.1 水平扩展2.2 垂直扩展2.3 弹性扩展 三、可靠性(Rel…...

测试在 Oracle 下直接 rm dbf 数据文件并重启数据库
创建一个新的表空间并创建新的用户,指定新表空间为新用户的默认表空间 create tablespace zzw datafile /oradata/cesdb/zzw01.dbf size 10m;zzw用户已经创建过,这里修改其默认表空间 alter user zzw quota unlimited on zzw; alter user zzw default …...

【开源】基于JAVA的计算机机房作业管理系统
项目编号: S 017 ,文末获取源码。 \color{red}{项目编号:S017,文末获取源码。} 项目编号:S017,文末获取源码。 目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 登录注册模块2.2 课程管理模块2.3 课…...

Ubuntu 配置静态 IP
Ubuntu 18 开始可以使用netplan配置网络。配置文件位于/etc/netplan/xxx.yaml中,netplan默认是使用NetworkManager来配置网卡信息的。 修改配置文件: 1、打开文件编辑:sudo vi 01-network-manager-all.yaml原文件内容如下:netwo…...

Spring Cloud实战 |分布式系统的流量控制、熔断降级组件Sentinel如何使用
专栏集锦,大佬们可以收藏以备不时之需 Spring Cloud实战专栏:https://blog.csdn.net/superdangbo/category_9270827.html Python 实战专栏:https://blog.csdn.net/superdangbo/category_9271194.html Logback 详解专栏:https:/…...
第六届 传智杯初赛B组
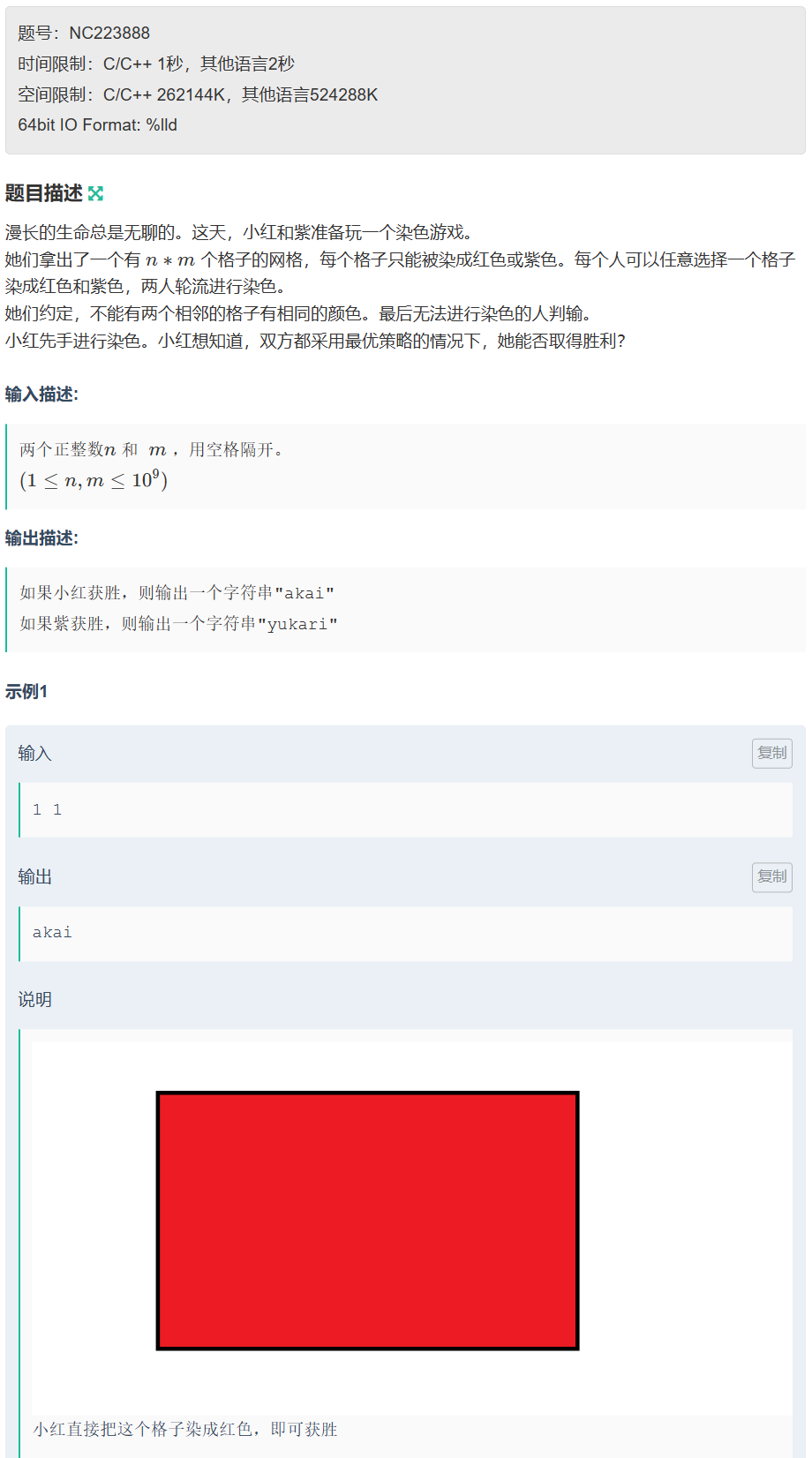
文章目录 A. 字符串拼接🍻 AC code B. 最小差值🍻 AC code C. 红色和紫色🍻 AC code D. abb🍻 AC code E. kotori和素因子🍻 AC code F. 红和蓝🍻 AC code 🥰 Tips:AI可以把代码从 j…...
文档向量化工具(二):text2vec介绍
目录 前言 text2vec开源项目 核心能力 文本向量表示模型 本地试用 安装依赖 下载模型到本地(如果你的网络能直接从huggingface上拉取文件,可跳过) 运行试验代码 前言 在上一篇文章中介绍了,如何从不同格式的文件里提取…...

vscode中pylance无法显示outline无法跳转
当打开的workspce中有较多的文件时,pylance需要分析的文件太多,导致卡住,无法分析到对应的python文件 常见的情况是,当我们在workspace中包含了data文件夹(通常是通过软连接方式把数据集链接过来)…...

番外篇之通讯录
前言:用到的知识点有枚举、结构体、数组,快速排序(用的名字排序) 下面是测试函数: test.c #define _CRT_SECURE_NO_WARNINGS 1 #include"contact.h" void menu() {printf("*************************…...
学生信息管理系统程序Python
系统主界面 在该界面中可以选择要使用功能对应的菜单进行不同的操作。在选择功能菜单时,有两种方法, 一种是输入1,另一种是按下键盘上的↑或↓方向键进行选择。这两种方法的结果是一样的,所以使用哪种方法都可以。 (…...

[js] for forEach for of 循环里await关键字的用法
1、for:循环中使用await的写法(生效) async function loop(){for( let i0; i<array.length; i ){let datas await getDatas()break} }2、forEach:循环中使用await的写法(不生效): array.f…...

Linux面试题(二)
目录 17、怎么使一个命令在后台运行? 18、利用 ps 怎么显示所有的进程? 怎么利用 ps 查看指定进程的信息? 19、哪个命令专门用来查看后台任务? 20、把后台任务调到前台执行使用什么命令?把停下的后台任务在后台执行起来用什么命令? 21、终止进程用什么命令…...
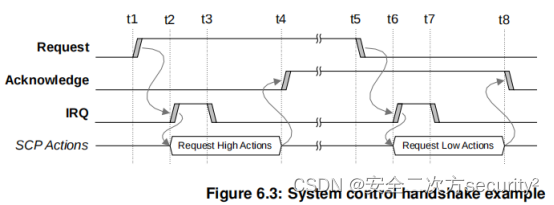
电源控制系统架构(PCSA)之系统控制处理器组件
目录 6.4 系统控制处理器 6.4.1 SCP组件 SCP处理器Core SCP处理器Core选择 SCP处理器核内存 系统计数器和通用计时器 看门狗 电压调节器控制 时钟控制 系统控制 信息接口 电源策略单元 传感器控制 外设访问 系统访问 6.4 系统控制处理器 系统控制处理器(SCP)是…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...
