【算法】FFT-1(递归实现)(不包括IFFT)
FFT
- 多项式
- 多项式乘法
- 复数及运算
- 导数
- 泰勒公式及展开式
- 欧拉公式
- 单位根
- FFT
- Code
- IFFT
多项式
我们从课本中可以知道,一个 n − 1 n-1 n−1 次的多项式可以写成 a 0 + a 1 x + a 2 x 2 + a 3 x 3 + ⋯ + a n − 1 x n − 1 a_{0}+a_{1}x+a_{2}x^2+a_{3}x^3+\dots+a_{n-1}x^{n-1} a0+a1x+a2x2+a3x3+⋯+an−1xn−1
用高级一点的表示法就是:
一个 n − 1 n-1 n−1 次 n n n 项多项式 f ( x ) f(x) f(x) 可以表示为:
f ( x ) = ∑ i = 0 n − 1 a i x i f(x)=\sum_{i=0}^{n-1}a_ix^i f(x)=∑i=0n−1aixi
所以我们可以用每一项的系数来表示 f ( x ) f(x) f(x),即
f ( x ) = { a 0 , a 1 , a 2 , … , a n − 1 } f(x)=\{a_0,a_1,a_2,\dots,a_{n-1}\} f(x)={a0,a1,a2,…,an−1}
俗称系数表示法。
但是,当我们把这个多项式看成一个函数时,我们将 n n n 个不同的 x x x 带入,会得到 n n n 个不一样的 y y y,而我们就得到了 n n n 个点的坐标,它们确定唯一的多项式 f ( x ) f(x) f(x)
证明很简单,直接待定系数法就可以解决。
那么 f ( x ) f(x) f(x) 还可以用这 n n n 个点表示:
f ( x ) = { ( x 0 , y 0 ) , ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x n − 1 , y n − 1 ) } f(x)=\{(x_0,y_0),(x_1,y_1),(x_2,y_2),\dots,(x_{n-1},y_{n-1})\} f(x)={(x0,y0),(x1,y1),(x2,y2),…,(xn−1,yn−1)}
(其中 y i = f ( x i ) y_i=f(x_i) yi=f(xi))
俗称点值表示法。
多项式乘法
对于两个系数表示法表示的多项式 f ( x ) f(x) f(x) 和 g ( x ) g(x) g(x),如果要计算它们的乘积 h ( x ) h(x) h(x),我们需要枚举 f ( x ) f(x) f(x) 的每一项和 g ( x ) g(x) g(x) 的每一项相乘,最后累计,时间复杂度 O ( n 2 ) O(n^2) O(n2)
那么换成点值表示呢?时间复杂度为 O ( n ) O(n) O(n)
Why?
设两个多项式 f ( x ) f(x) f(x) 和 g ( x ) g(x) g(x) 分别为:
f ( x ) = { ( x 0 , y 1 0 ) , ( x 1 , y 1 1 ) , ( x 2 , y 1 2 ) , … , ( x n − 1 , y 1 n − 1 ) } f(x)=\{(x_0,y1_0),(x_1,y1_1),(x_2,y1_2),\dots,(x_{n-1},y1_{n-1})\} f(x)={(x0,y10),(x1,y11),(x2,y12),…,(xn−1,y1n−1)}
(其中 y 1 i = f ( x i ) y1_i=f(x_i) y1i=f(xi))
g ( x ) = { ( x 0 , y 2 0 ) , ( x 1 , y 2 1 ) , ( x 2 , y 2 2 ) , … , ( x n − 1 , y 2 n − 1 ) } g(x)=\{(x_0,y2_0),(x_1,y2_1),(x_2,y2_2),\dots,(x_{n-1},y2_{n-1})\} g(x)={(x0,y20),(x1,y21),(x2,y22),…,(xn−1,y2n−1)}
(其中 y 2 i = g ( x i ) y2_i=g(x_i) y2i=g(xi))
那么结果 h ( x ) h(x) h(x) 为:
h ( x ) = { ( x 0 , y 2 0 ⋅ y 1 0 ) , ( x 1 , y 2 1 ⋅ y 1 1 ) , ( x 2 , y 2 2 ⋅ y 1 2 ) , … , ( x n − 1 , y 2 n − 1 ⋅ y 1 n − 1 ) } h(x)=\{(x_0,y2_0 \cdot y1_0),(x_1,y2_1 \cdot y1_1),(x_2,y2_2 \cdot y1_2),\dots,(x_{n-1},y2_{n-1} \cdot y1_{n-1})\} h(x)={(x0,y20⋅y10),(x1,y21⋅y11),(x2,y22⋅y12),…,(xn−1,y2n−1⋅y1n−1)}
好,我们就结束了
但是怎么将系数表示法转换为点值表示法呢?
复数及运算
高中课本里讲过复数,不过不知道也没关系,这里会讲。
定义:复数单位 i i i 满足 i 2 = − 1 i^2=-1 i2=−1,则形如 a + b i a+bi a+bi 的数为复数。 ( a , b ∈ R ) (a,b\in R) (a,b∈R)
其中 a a a 叫做实部, b b b 叫做虚部, i i i 为虚数单位。
所以有 − 7 = 7 i \sqrt{-7}=\sqrt7i −7=7i
类似平面直角坐标系,在复平面直角坐标系中,复数为其中的一个点。
如下图:
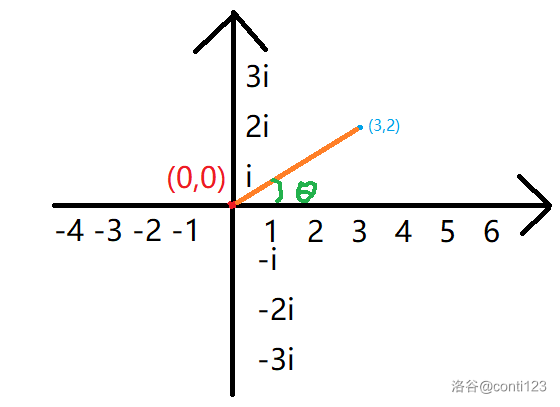
点(3,2)表示的复数为 3 + 2 i 3+2i 3+2i
它也可以表示为( 1 3 , θ \sqrt 13,\theta 13,θ)
定义:一个复数的模为它到原点的距离。
及复数 z = a + b i z=a+bi z=a+bi 的模记为 ∣ z ∣ = a 2 + b 2 |z|=\sqrt{a^2+b^2} ∣z∣=a2+b2
一个复数的共轭复数为其虚部取反。
及复数 z = a + b i z=a+bi z=a+bi 的共轭复数为 z ˉ = a − b i \bar{z}=a-bi zˉ=a−bi, z z ˉ = a 2 + b 2 z \bar{z} = a^2 +b^2 zzˉ=a2+b2
其实就跟共轭根式差不多。
复数的运算其实跟实数的运算差不多。
设 z 1 = a + b i z_1 = a + bi z1=a+bi, z 2 = c + d i z_2 = c + di z2=c+di
加减法:实部和虚部分别相加减:
z 1 ± z 2 = ( a ± c ) + ( b ± d ) i z_1 \pm z_2 = (a \pm c) + (b \pm d)i z1±z2=(a±c)+(b±d)i
乘法:硬算出奇迹(拆完后合并同类项)
z 1 z 2 = ( a c − b d ) + ( b c + a d ) i z_1z_2 = (ac - bd) + (bc + ad)i z1z2=(ac−bd)+(bc+ad)i
( a 1 , θ 1 ) ( a 2 , θ 2 ) = ( a 1 a 2 , θ 1 + θ 2 ) (a_1,\theta_1)(a_2,\theta_2)=(a_1a_2,\theta_1+\theta_2) (a1,θ1)(a2,θ2)=(a1a2,θ1+θ2)
除法:化简
z 1 z 2 = a + b i c + d i = ( a + b i ) ( c − d i ) ( c + d i ) ( c − d i ) = a c − b d i 2 + b c i − a d i c 2 − d 2 i 2 = ( a c + b d ) + ( b c − a d ) i c 2 + d 2 \dfrac{z_1}{z_2} = \dfrac{a+bi}{c+di}=\dfrac{(a+bi)(c-di)}{(c+di)(c-di)}=\dfrac{ac-bdi^2+bci-adi}{c^2-d^2i^2}=\dfrac{(ac+bd)+(bc-ad)i}{c^2+d^2} z2z1=c+dia+bi=(c+di)(c−di)(a+bi)(c−di)=c2−d2i2ac−bdi2+bci−adi=c2+d2(ac+bd)+(bc−ad)i
导数
和初中的 y = … y=\dots y=… 不一样,我们用 f ( x ) f(x) f(x) 来表示一个关于 x x x 的函数。
一般地,已知函数 y = f ( x ) y=f(x) y=f(x), x 0 , x 1 x_0,x_1 x0,x1 是其定义域内不同两点,记 Δ x = x 1 − x 0 , Δ y = y 1 − y 0 = f ( x 1 ) − f ( x 0 ) = f ( x 0 + Δ x ) − f ( x 0 ) \Delta x=x_1-x_0,\Delta y=y_1-y_0=f(x_1)-f(x_0)=f(x_0+\Delta x)-f(x_0) Δx=x1−x0,Δy=y1−y0=f(x1)−f(x0)=f(x0+Δx)−f(x0),则当 Δ x ≠ 0 \Delta x\neq 0 Δx=0 时,商 f ( x 0 + Δ x ) − f ( x 0 ) Δ x = Δ y Δ x \frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}=\frac{\Delta y}{\Delta x} Δxf(x0+Δx)−f(x0)=ΔxΔy 称作函数 y = f ( x ) y=f(x) y=f(x)在区间 $[x_0,x_0 +_\Delta x] $ 上的平均变化率。
当 Δ x \Delta x Δx 趋近于 0 0 0 时,平均变化率 Δ y Δ x = f ( x 0 + Δ x ) − f ( x 0 ) Δ x \frac{\Delta y}{\Delta x}=\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x} ΔxΔy=Δxf(x0+Δx)−f(x0) 趋近于一个常数 l l l,那么常数 l l l 称为函数 f ( x ) f(x) f(x) 在点 x 0 x_0 x0 的瞬时变化率。
趋近于可以用符号 → \to → 表示,所以上面那句话可以这样表示:
当 Δ x → 0 \Delta x \to 0 Δx→0 时, f ( x 0 + Δ x ) − f ( x 0 ) Δ x → l \frac{f(x_0+\Delta x)-f(x_0)}{\Delta x} \to l Δxf(x0+Δx)−f(x0)→l
或记作:
lim Δ x → 0 f ( x 0 + Δ x ) − f ( x 0 ) Δ x = l \lim_{\Delta x \to 0} \frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}=l limΔx→0Δxf(x0+Δx)−f(x0)=l
函数在 x 0 x_0 x0 的瞬时变化率,通常称为 f ( x ) f(x) f(x) 在 x = x 0 x=x_0 x=x0 处的导数,并记作 f ′ ( x 0 ) f'(x_0) f′(x0)。
注意,是 f ′ f' f′。
那么对于函数 f ( x ) f(x) f(x) 怎么求导呢?
如下:
{ ( x a ) ′ = a x a − 1 ( c ) ′ = 0 ( e x ) ′ = e x ( ln x ) ′ = 1 x ( sin x ) ′ = cos x ( cos x ) ′ = sin x } \begin{Bmatrix} (x^a)'=ax^{a-1} \\ (c)'=0 \\ (e^x)'=e^x \\ (\ln x)'=\frac{1}{x} \\ (\sin x)'=\cos x \\ (\cos x)'=\sin x \end{Bmatrix} ⎩ ⎨ ⎧(xa)′=axa−1(c)′=0(ex)′=ex(lnx)′=x1(sinx)′=cosx(cosx)′=sinx⎭ ⎬ ⎫
例如 f ( x ) = x 2 f(x)=x^2 f(x)=x2,则 f ′ ( x ) = 2 x f'(x)=2x f′(x)=2x
最后再说一点 f ′ ( x ) f'(x) f′(x) 表示函数 f ( x ) f(x) f(x) 在 x x x 取值为几时切线的斜率。
泰勒公式及展开式
泰勒公式:
f ( x ) = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) + f ′ ′ ( x 0 ) 2 ! ( x − x 0 ) 2 + ⋯ + f ( n ) ( x 0 ) n ! ( x − x 0 ) n + R n + 1 ( x ) f(x)=f(x_0)+f'(x_0)(x-x_0)+\frac{f''(x_0)}{2!}(x-x_0)^2+\dotsb +\frac{f^{(n)}(x_0)}{n!}(x-x_0)^n+R_{n+1}(x) f(x)=f(x0)+f′(x0)(x−x0)+2!f′′(x0)(x−x0)2+⋯+n!f(n)(x0)(x−x0)n+Rn+1(x)
其中 R R R 为误差。
那么当 x 0 = 0 x_0=0 x0=0 时,得到麦克劳林公式:
f ( x ) = f ( 0 ) + f ′ ( 0 ) x + f ′ ′ ( 0 ) 2 ! x 2 + ⋯ + f ( n ) ( 0 ) n ! x n + R n + 1 ( x ) f(x)=f(0)+f'(0)x+\frac{f''(0)}{2!}x^2+\dotsb +\frac{f^{(n)}(0)}{n!}x^n+R_{n+1}(x) f(x)=f(0)+f′(0)x+2!f′′(0)x2+⋯+n!f(n)(0)xn+Rn+1(x)
所以我们就有了以下几个展开式:
{ e x = 1 + x + x 2 2 ! + x 3 3 ! + ⋯ + x n n ! + ⋯ ln ( 1 + x ) = x − x 2 2 + x 3 3 + ⋯ + ( − 1 ) n − 1 x n n + ⋯ sin x = ∑ k = 0 ∞ ( − 1 ) k x 2 k + 1 ( 2 k + 1 ) ! cos x = ∑ k = 0 ∞ ( − 1 ) k x 2 k ( 2 k ) ! } \begin{Bmatrix} e^x=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\dotsb+\frac{x^n}{n!}+\dotsb \\ \ln(1+x)=x-\frac{x^2}{2}+\frac{x^3}{3}+\dotsb+(-1)^{n-1}\frac{x^n}{n}+\dotsb \\ \sin x=\sum_{k=0}^{\infty}(-1)^k\frac{x^{2k+1}}{(2k+1)!} \\ \cos x=\sum_{k=0}^{\infty}(-1)^k\frac{x^{2k}}{(2k)!} \end{Bmatrix} ⎩ ⎨ ⎧ex=1+x+2!x2+3!x3+⋯+n!xn+⋯ln(1+x)=x−2x2+3x3+⋯+(−1)n−1nxn+⋯sinx=∑k=0∞(−1)k(2k+1)!x2k+1cosx=∑k=0∞(−1)k(2k)!x2k⎭ ⎬ ⎫
欧拉公式
接上文,展开 e i x e^{ix} eix,得:
e i x = 1 + i x − x 2 2 ! − i x 3 3 ! + x 4 4 ! + i x 5 5 ! − x 6 6 ! − i x 7 7 ! + ⋯ ) e^{ix}=1+ix-\frac{x^2}{2!}-i\frac{x^3}{3!}+\frac{x^4}{4!}+i\frac{x^5}{5!}-\frac{x^6}{6!}-i\frac{x^7}{7!}+\dotsb) eix=1+ix−2!x2−i3!x3+4!x4+i5!x5−6!x6−i7!x7+⋯)
e i x = ( 1 − x 2 2 ! + x 4 4 ! − x 6 6 ! + ⋯ ) + i ( x − x 3 3 ! + x 5 5 ! − 7 3 7 ! + ⋯ ) e^{ix}=(1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\dotsb) +i(x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{7^3}{7!}+\dotsb) eix=(1−2!x2+4!x4−6!x6+⋯)+i(x−3!x3+5!x5−7!73+⋯)
e i x = cos x + i sin x e^{ix}=\cos x+i\sin x eix=cosx+isinx
将 x = π x=\pi x=π 带入:
e i π = cos π + i sin π = − 1 e^{i\pi}=\cos \pi + i\sin \pi=-1 eiπ=cosπ+isinπ=−1
所以欧拉恒等式出来:
e i π + 1 = 0 e^{i\pi}+1=0 eiπ+1=0
单位根
设 n n n 为正整数,若 x n = 1 x^n=1 xn=1 ,则 x x x 是 n n n 次单位根。
下文默认 n = 2 m , m n=2^m,m n=2m,m为正整数。
根据上文的欧拉公式,我们可知 e 2 k π i = cos 2 k π + i sin 2 k π = 1 e^{2k \pi i}=\cos 2k\pi+i\sin 2k\pi=1 e2kπi=cos2kπ+isin2kπ=1,故 n n n 次单位根分别是: e 2 k π i n = cos 2 k π n + i sin 2 k π n , ( k = 0 , 1 , 2 , … , n − 1 ) e^{\frac{2k\pi i}{n}}=\cos \frac{2k\pi}{n}+i\sin \frac{2k\pi}{n},(k=0,1,2,\dots,n-1) en2kπi=cosn2kπ+isinn2kπ,(k=0,1,2,…,n−1)。
接上文复数的知识,每个单位根在复平面上的坐标为 ( cos 2 k π n , sin 2 k π n ) (\cos \frac{2k\pi}{n},\sin \frac{2k\pi}{n}) (cosn2kπ,sinn2kπ)。
如图: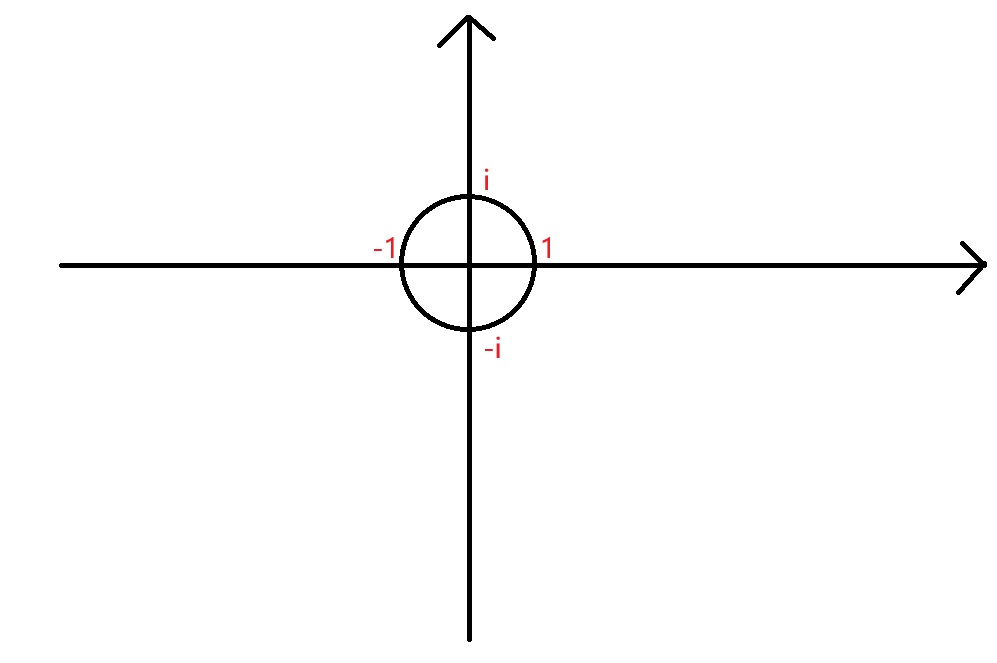
在一个标准复平面坐标系上,以 1 1 1 为半径画一个圆, n n n次单位根可以想象为把这个圆平分为 n n n 分中每一个点。
我们用 ω n 1 , ω n 2 , ω n 3 , … , ω n n \omega_n^1,\omega_n^2,\omega_n^3,\dots,\omega_n^n ωn1,ωn2,ωn3,…,ωnn 来表示 n n n 次单位根的每一个根,及方程的每一个解。
所以有 ω n k = cos k 2 π n + i sin k 2 π n \omega_n^k=\cos k\frac{2\pi}{n}+i\sin k\frac{2\pi}{n} ωnk=coskn2π+isinkn2π
如当 n = 4 n=4 n=4时, ω 4 = 1 , − 1 , i , − 1 \omega_4=1,-1,i,-1 ω4=1,−1,i,−1
如当 n = 1 n=1 n=1 时, ω 1 = 1 \omega_1=1 ω1=1
单位根的性质:
ω 2 n 2 k = ω n k = − ω n k + n 2 \omega_{2n}^{2k}=\omega_{n}^{k}=-\omega _n^{k+\frac{n}{2}} ω2n2k=ωnk=−ωnk+2n
ω n 0 = ω n n = 1 \omega_n^0=\omega_n^n=1 ωn0=ωnn=1
ω 2 n 2 k = cos 2 k 2 π 2 n + i sin 2 k 2 π 2 n = ω n k \omega_{2n}^{2k}=\cos 2k \frac{2\pi}{2n}+i\sin 2k \frac{2\pi}{2n}=\omega_n^k ω2n2k=cos2k2n2π+isin2k2n2π=ωnk
ω n n 2 = cos n 2 ⋅ 2 π n + i sin n 2 ⋅ 2 π n = cos π + i sin π = − 1 \omega_n^{\frac{n}{2}}=\cos \frac{n}{2}\cdot \frac{2\pi}{n}+i\sin \frac{n}{2}\cdot \frac{2\pi}{n}=\cos \pi+i\sin \pi=-1 ωn2n=cos2n⋅n2π+isin2n⋅n2π=cosπ+isinπ=−1
FFT
设 n n n 为偶数, k < n 2 k<\frac{n}{2} k<2n。
设
A ( x ) = a 0 + a 1 x + a 2 x 2 + a 3 x 3 + ⋯ + a n − 1 x n − 1 A(x)=a_{0}+a_{1}x+a_{2}x^2+a_{3}x^3+\dots+a_{n-1}x^{n-1} A(x)=a0+a1x+a2x2+a3x3+⋯+an−1xn−1
A 1 ( x ) = a 0 + a 2 x + a 4 x 2 + ⋯ + a n − 2 x n 2 − 1 A_1(x)=a_0+a_2x+a_4x^2+\cdots+a_{n-2}x^{\frac{n}{2}-1} A1(x)=a0+a2x+a4x2+⋯+an−2x2n−1
A 2 ( x ) = a 1 + a 3 x + a 5 x 2 + ⋯ + a n − 1 x n 2 − 1 A_2(x)=a_1+a_3x+a_5x^2+\cdots+a_{n-1}x^{\frac{n}{2}-1} A2(x)=a1+a3x+a5x2+⋯+an−1x2n−1
所以有:
A ( x ) = A 1 ( x 2 ) + x A 2 ( x 2 ) A(x)=A_1(x^2)+xA_2(x^2) A(x)=A1(x2)+xA2(x2)
A ( ω n k ) = A 1 ( ω n 2 k ) + ω n k A 2 ( ω n 2 k ) A(\omega_n^k)=A_1(\omega_n^{2k})+\omega_n^kA_2(\omega_n^{2k}) A(ωnk)=A1(ωn2k)+ωnkA2(ωn2k)
A ( ω n k + n 2 ) = A 1 ( ω n 2 k + n ) + ω n k + n 2 A 2 ( ω n 2 k + n ) = A 1 ( ω n 2 k ) − ω n k A 2 ( ω n 2 k ) A(\omega_n^{k+\frac{n}{2}})=A_1(\omega_n^{2k+n})+\omega_n^{k+\frac{n}{2}}A_2(\omega_n^{2k+n})=A_1(\omega_n^{2k})-\omega_n^kA_2(\omega_n^{2k}) A(ωnk+2n)=A1(ωn2k+n)+ωnk+2nA2(ωn2k+n)=A1(ωn2k)−ωnkA2(ωn2k)
发现了什么?没错,只有后面一坨是相反的,这说明我们可以 O ( 1 ) O(1) O(1) 通过第一个式子得出第二个式子
所以 k k k 只要枚举前 n 2 \frac{n}{2} 2n 个数就可以了,问题缩小了一半,而缩小后还能继续缩小,所以我们用类似线段树的分治(递归)来解决它,时间复杂度 O ( n log n ) O(n\log n) O(nlogn)
Code
void fft(int limit,complex *a,int type)
{if(limit==1) return ;complex a1[limit>>1],a2[limit>>1];for(int i=0;i<=limit;i+=2)a1[i>>1]=a[i],a2[i>>1]=a[i+1];fft(limit>>1,a1,type);fft(limit>>1,a2,type);complex Wn=complex(cos(2.0*Pi/limit),type*sin(2.0*Pi/limit)),w=complex(1,0);for(int i=0;i<(limit>>1);i++,w=w*Wn)a[i]=a1[i]+w*a2[i],a[i+(limit>>1)]=a1[i]-w*a2[i];
}
IFFT
但是光有点值还是不够的,我们还要转换为数值,这就是 IFFT。
至于还有一个迭代优化。
我们下篇博客再讲。
相关文章:

【算法】FFT-1(递归实现)(不包括IFFT)
FFT 多项式多项式乘法复数及运算导数泰勒公式及展开式欧拉公式单位根 FFTCode IFFT 多项式 我们从课本中可以知道,一个 n − 1 n-1 n−1 次的多项式可以写成 a 0 a 1 x a 2 x 2 a 3 x 3 ⋯ a n − 1 x n − 1 a_{0}a_{1}xa_{2}x^2a_{3}x^3\dotsa_{n-1}x^{n-…...

大模型训练效率提升至2.6倍,腾讯Angel机器学习框架升级
在算力紧缺的背景下,如何提升大模型训练和推理的效率,并降低成本,成为业界关注的焦点。 11月23日,腾讯披露,腾讯混元大模型背后的自研机器学习框架Angel再次升级,大模型训练效率提升至主流开源框架的2.6倍…...

【方块消消乐】方块消除游戏-微信小程序开发流程详解
有做过俄罗斯方块游戏小程序的经验,这次有做了一个消灭方块的游戏,实现过程很顺利,游戏看着和之前做的俄罗斯方块游戏很像,这里调整了玩法,试玩感觉还可以,接下来给大家讲一讲消灭方块游戏开发过程。 俄罗斯…...

mybatis配置文件中配置类型别名的方式
在MyBatis配置文件(通常是mybatis-config.xml)中,可以通过以下方式配置类型别名: 1. 使用typeAliases元素配置全局类型别名 <configuration> <typeAliases> <typeAlias alias"YourAlias" type"…...

leetcode目标和
给你一个非负整数数组 nums 和一个整数 target 。 向数组中的每个整数前添加 ‘’ 或 ‘-’ ,然后串联起所有整数,可以构造一个 表达式 : 例如,nums [2, 1] ,可以在 2 之前添加 ‘’ ,在 1 之前添加 ‘-…...
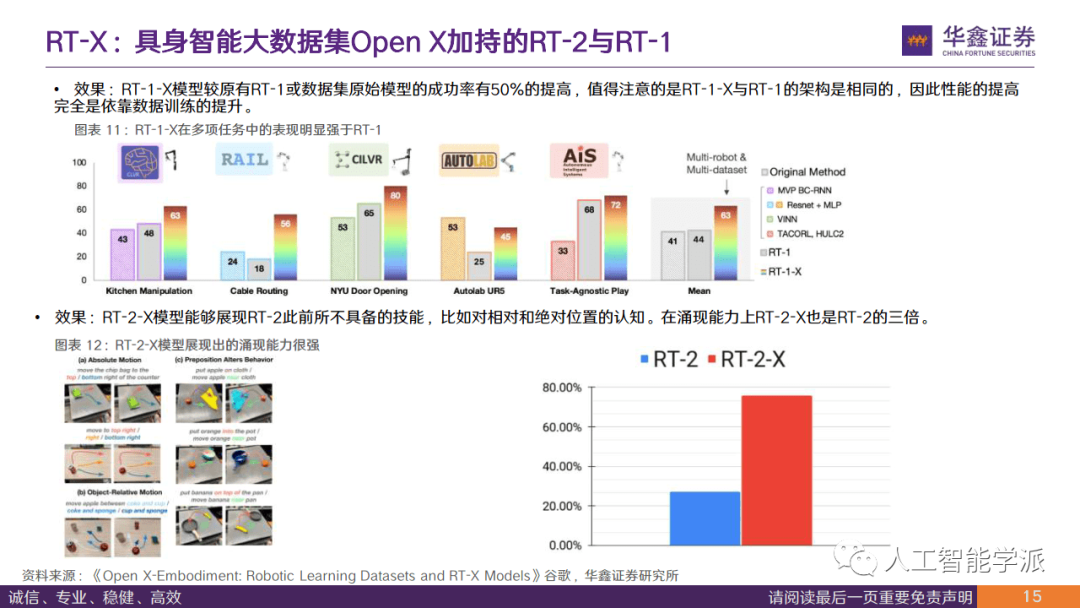
2023人形机器人行业海外科技研究:从谷歌看机器人大模型进展
今天分享的是人形机器人系列深度研究报告:《2023人形机器人行业海外科技研究:从谷歌看机器人大模型进展》。 (报告出品方:华鑫证券) 报告共计:26页 大模型是人形机器人的必备要素 长期来看,人…...

【深度学习笔记】01 数据操作与预处理
01 数据操作与预处理 一、数据操作1.1 基本数据操作1.2 广播机制1.3 索引和切片1.4 节省内存1.5 转换为其他Python对象 二、数据预处理读取数据集处理缺失值转换为张量格式练习 一、数据操作 1.1 基本数据操作 导入torch import torch张量表示一个由数值组成的数组ÿ…...

Python与设计模式--门面模式
8-Python与设计模式–门面模式 一、火警报警器(1) 假设有一组火警报警系统,由三个子元件构成:一个警报器,一个喷水器, 一个自动拨打电话的装置。其抽象如下: class AlarmSensor:def run(self):…...
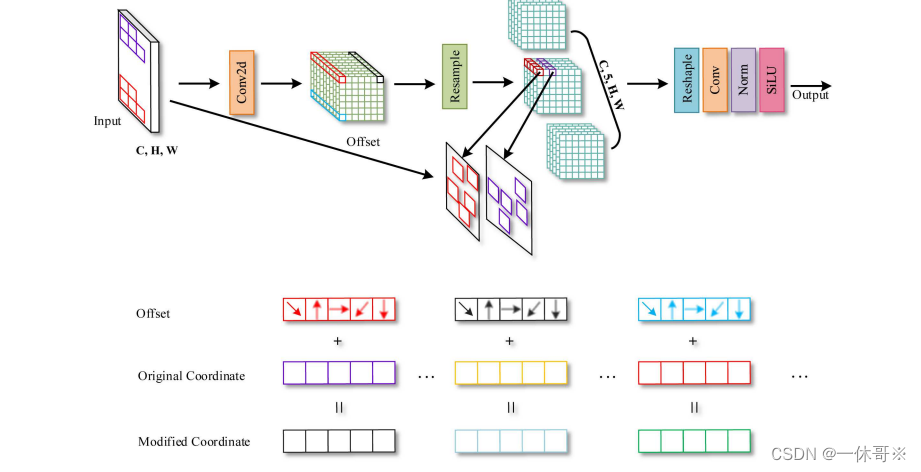
改进YOLOv8 | YOLOv5系列:RFAConv续作,即插即用具有任意采样形状和任意数目参数的卷积核AKCOnv
RFAConv续作,构建具有任意采样形状的卷积AKConv 一、论文yolov5加入的方式论文 源代码 一、论文 基于卷积运算的神经网络在深度学习领域取得了显著的成果,但标准卷积运算存在两个固有缺陷:一方面,卷积运算被限制在一个局部窗口,不能从其他位置捕获信息,并且其采样形状是…...
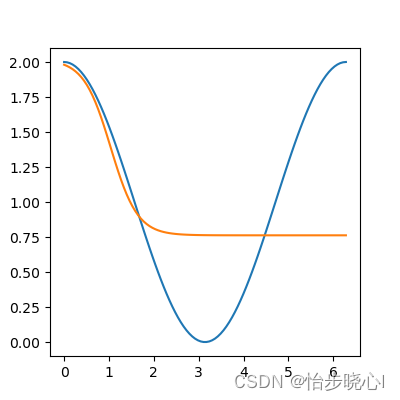
机器学习-激活函数的直观理解
机器学习-激活函数的直观理解 在机器学习中,激活函数(Activation Function)是用于引入非线性特性的一种函数,它在神经网络的每个神经元上被应用。 如果不使用任何的激活函数,那么神经元的响应就是wxb,相当…...
Fedora 36 ARM 镜像源更换与软件安装
1、什么是Fedora Fedora Linux是较具知名度的Linux发行套件之一,由Fedora专案社群开发、红帽公司赞助,目标是建立一套新颖、多功能并且自由的作业系统。 Fedora是商业化的Red Hat Enterprise Linux发行版的上游原始码。 2、Fedora软件安装 64 位 .deb&a…...

多级缓存快速上手
哈喽~大家好,这篇来看看多级缓存。 🥇个人主页:个人主页 🥈 系列专栏:【微服务】 🥉与这篇相关的文章: JAVA进程和线程JAVA进程和线程-CSDN博客Http…...

初始React
<!DOCTYPE html> <html> <head> <meta charset"UTF-8" /> <title>React</title> </head> <body> 了解React <!-- React是一个用于构建web和原生态交互界面的库 相对于传统DOM开发优势:组件化开发…...

2.5 逆矩阵
一、逆矩阵的注释 假设 A A A 是一个方阵,其逆矩阵 A − 1 A^{-1} A−1 与它的大小相同, A − 1 A I A^{-1}AI A−1AI。 A A A 与 A − 1 A^{-1} A−1 会做相反的事情。它们的乘积是单位矩阵 —— 对向量无影响,所以 A − 1 A x x A^{…...
物流实时数仓:数仓搭建(ODS)
系列文章目录 物流实时数仓:采集通道搭建 物流实时数仓:数仓搭建 文章目录 系列文章目录前言一、IDEA环境准备1.pom.xml2.目录创建 二、代码编写1.log4j.properties2.CreateEnvUtil.java3.KafkaUtil.java4.OdsApp.java 三、代码测试总结 前言 现在我们…...

【ARM 嵌入式 编译 Makefile 系列 18 -- Makefile 中的 export 命令详细介绍】
文章目录 Makefile 中的 export 命令详细介绍Makefile 使用 export导出与未导出变量的区别示例:导出变量以供子 Makefile 使用 Makefile 中的 export 命令详细介绍 在 Makefile 中,export 命令用于将变量从 Makefile 导出到由 Makefile 启动的子进程的环…...

【opencv】计算机视觉:停车场车位实时识别
目录 目标 整体流程 背景 详细讲解 目标 我们想要在一个实时的停车场监控视频中,看看要有多少个车以及有多少个空缺车位。然后我们可以标记空的,然后来车之后,实时告诉应该停在那里最方便、最近!!!实现…...
:FFmpeg与SDL环境配置)
播放器开发(三):FFmpeg与SDL环境配置
学习课题:逐步构建开发播放器【QT5 FFmpeg6 SDL2】 环境配置 我这边的是使用macOS;IDE用的是CLion;CMake构建,除了创建项目步骤、CMakeLists文件有区别之外的代码层面不会有太大区别。 配置上只添加一下CMakeLists中FFmpeg和SD…...
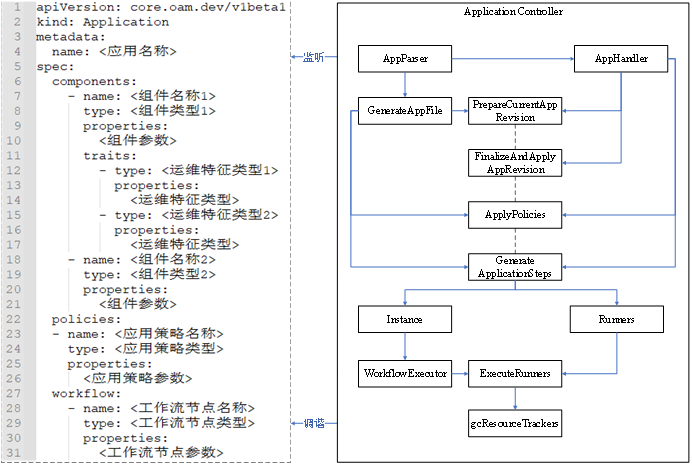
KubeVela核心控制器原理浅析
前言 在学习 KubeVela 的核心控制器之前,我们先简单了解一下 KubeVela 的相关知识。 KubeVela 本身是一个应用交付与管理控制平面,它架在 Kubernetes 集群、云平台等基础设施之上,通过开放应用模型来对组件、云服务、运维能力、交付工作流进…...

迎接“全全闪”时代 XSKY星辰天合发布星海架构和星飞产品
11 月 17 日消息,北京市星辰天合科技股份有限公司(简称:XSKY星辰天合)在北京首钢园举办了主题为“星星之火”的 XSKY 星海全闪架构暨星飞存储发布会。 (图注:XSKY星辰天合 CEO 胥昕) XSKY星辰天…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...
