LeetCode 统计美丽子字符串 II【质因子分解,前缀和,哈希表】困难
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章中,我不仅会讲解多种解题思路及其优化,还会用多种编程语言实现题解,涉及到通用解法时更将归纳总结出相应的算法模板。
为了方便在PC上运行调试、分享代码文件,我还建立了相关的仓库:https://github.com/memcpy0/LeetCode-Conquest。在这一仓库中,你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等,还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解,还可以一同分享给他人。
由于本系列文章的内容随时可能发生更新变动,欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。
给你一个字符串 s 和一个正整数 k 。
用 vowels 和 consonants 分别表示字符串中元音字母和辅音字母的数量。
如果某个字符串满足以下条件,则称其为 美丽字符串 :
vowels == consonants,即元音字母和辅音字母的数量相等。(vowels * consonants) % k == 0,即元音字母和辅音字母的数量的乘积能被k整除。
返回字符串 s 中 非空美丽子字符串 的数量。
子字符串是字符串中的一个连续字符序列。
英语中的 元音字母 为 'a'、'e'、'i'、'o' 和 'u' 。
英语中的 辅音字母 为除了元音字母之外的所有字母。
示例 1:
输入:s = "baeyh", k = 2
输出:2
解释:字符串 s 中有 2 个美丽子字符串。
- 子字符串 "b_aeyh_",vowels = 2(["a","e"]),consonants = 2(["y","h"])。
可以看出字符串 "aeyh" 是美丽字符串,因为 vowels == consonants 且 vowels * consonants % k == 0 。
- 子字符串 "_baey_h",vowels = 2(["a","e"]),consonants = 2(["b","y"])。
可以看出字符串 "baey" 是美丽字符串,因为 vowels == consonants 且 vowels * consonants % k == 0 。
可以证明字符串 s 中只有 2 个美丽子字符串。
示例 2:
输入:s = "abba", k = 1
输出:3
解释:字符串 s 中有 3 个美丽子字符串。
- 子字符串 "_ab_ba",vowels = 1(["a"]),consonants = 1(["b"])。
- 子字符串 "ab_ba_",vowels = 1(["a"]),consonants = 1(["b"])。
- 子字符串 "_abba_",vowels = 2(["a","a"]),consonants = 2(["b","b"])。
可以证明字符串 s 中只有 3 个美丽子字符串。
示例 3:
输入:s = "bcdf", k = 1
输出:0
解释:字符串 s 中没有美丽子字符串。
提示:
1 <= s.length <= 5 * 10^41 <= k <= 1$0$s仅由小写英文字母组成。
解法 分解质因子+前缀和+哈希表
把元音视作 1 1 1,辅音视作 − 1 -1 −1 。「元音字母和辅音字母的数量相等」就等价于:找到一个和为 0 0 0 的连续子数组。注意这种子数组的长度一定是偶数,因为元音辅音数量相等。
设子数组的长度为 L L L 。由于元音辅音数量相等,所以元音辅音数量都等于 L 2 \dfrac{L}{2} 2L ,所以「元音字母和辅音字母的数量的乘积能被 k k k 整除」等价于
( L 2 ) 2 m o d k = 0 \left(\dfrac{L}{2}\right)^2 \bmod k = 0 (2L)2modk=0
这等价于
L 2 m o d ( 4 k ) = 0 L^2 \bmod (4k) = 0 L2mod(4k)=0
这个平方很烦人,如果能去掉平方就好做了。
这里得来点数学。我们来研究下,如果一个数 L L L 的平方能被 n n n 整除,意味着什么?
- 假设 n n n 是一个质数,例如 3 3 3,那么 L L L 必须包含质因子 3 3 3 ,此时问题就变成了:判断 L L L 能不能被 3 3 3 整除。我们把平方去掉了!
- 如果 n n n 是一个质数 $p 的 e e e 次幂呢?分类讨论:
- 如果 e e e是偶数,比如 n = 3 4 n=3^4 n=34 ,那么 L L L 必须包含因子 3 2 3^2 32 ,才能使得 L 2 L^2 L2 能被 n n n 整除。此时问题就变成了:判断 L L L 能不能被 3 2 3^2 32 整除。
- 如果 e e e 是奇数,比如 n = 3 5 n=3^5 n=35 ,那么 L L L 必须包含因子 3 3 3^3 33 ,才能使得 L 2 L^2 L2 能被 n n n 整除。此时问题就变成了:判断 L L L 能不能被 3 3 3^3 33 整除。
所以 L L L 必须包含因子 p r p^r pr ,其中 r = ⌈ e 2 ⌉ = ⌊ e + 1 2 ⌋ r=\left\lceil\dfrac{e}{2}\right\rceil = \left\lfloor\dfrac{e+1}{2}\right\rfloor r=⌈2e⌉=⌊2e+1⌋ 。
- 如果 n n n 可以分解出多个质因子,只需要把每个质因子及其幂次按照上面的方法处理,然后再相乘,就得到 L L L 必须包含什么因子。
继续
把 4 4 4 按照上述方法计算,设 L L L 必须包含因子 k ′ k' k′ 。现在问题变成,有多少个和为 0 0 0 的子数组,其长度是 k ′ k' k′ 的倍数?
设子数组的下标范围为 [ j , i ) [j,i) [j,i) ,那么其长度 L = i − j L=i-j L=i−j ,则有
( i − j ) m o d k ′ = 0 (i-j)\bmod k' = 0 (i−j)modk′=0
等价于
i m o d k ′ = j m o d k ′ i \bmod k' = j\bmod k' imodk′=jmodk′
对于元素和来说,相当于 s [ i ] − s [ j ] = 0 s[i]-s[j] = 0 s[i]−s[j]=0 ,即
s [ i ] = s [ j ] s[i] = s[j] s[i]=s[j]
我们需要同时满足这两个条件(下标模 k ′ k' k′ 相等, s s s 值相等),这可以一并用哈希表解决。哈希表的 k e y key key 是一个 p a i r pair pair : ( i m o d k ′ , s [ i ] ) (i\bmod k', s[i]) (imodk′,s[i]) ,哈希表的 v a l u e value value 是这个 p a i r pair pair 的出现次数。
代码实现时,前缀和数组可以用一个变量表示。
代码实现时,可以把 aeiou 压缩成一个二进制数,从而快速判断字母是否为元音。
问:为什么哈希表要在一开始插入一个 ( k ′ − 1 , 0 ) (k'-1, 0) (k′−1,0) ?
答:前缀和的第一项是 0 0 0,由于代码中是从下标 0 0 0 开始算第二个前缀和,所以相当于 s [ − 1 ] = 0 s[−1]=0 s[−1]=0 ,而 k ′ − 1 k'-1 k′−1 和 − 1 -1 −1 关于 k ′ k' k′ 同余,所以插入 ( k ′ − 1 , 0 ) (k′−1,0) (k′−1,0) 。
class Solution {
private:int pSqrt(int n) {int ans = 1;for (int i = 2; i * i <= n; ++i) {int i2 = i * i;while (n % i2 == 0) { // 质因数分解ans *= i; // L必须包含一个i^1n /= i2;}if (n % i == 0) { // 如果n包含某个质数的奇次幂ans *= i;n /= i;}}if (n > 1) ans *= n; // 剩下的最后1个质因子return ans;}struct PairHash {template<typename T1, typename T2>size_t operator() (const pair<T1, T2> &p) const {auto v1 = std::hash<T1>{}(p.first);auto v2 = std::hash<T2>{}(p.second);return v1 ^ v2;}};unordered_map<pair<int, int>, int, PairHash> cnt; //ok
public:int beautifulSubstrings(string s, int k) {k = pSqrt(k * 4); // 4k的质因数分解,求出L必须包含的因子值(多个质因子的幂次的乘积)const int aeiouMask = 1065233;cnt[ pair<int, int>{ k - 1, 0} ] = 1; // k-1和1同余int sum = 0;int ans = 0;for (int i = 0; i < s.size(); ++i) {char c = s[i];int bit = aeiouMask >> (c - 'a') & 1;sum += bit * 2 - 1; // 1->1, 0->-1auto p = pair{i % k, sum};ans += (long long)cnt[p];++cnt[p];}return ans;}
};
复杂度分析:
- 时间复杂度: O ( n + k ) \mathcal{O}(n + \sqrt k) O(n+k) ,其中 n n n 为 nums \textit{nums} nums 的长度。
- 空间复杂度: O ( n ) \mathcal{O}(n) O(n) 。
相关文章:

LeetCode 统计美丽子字符串 II【质因子分解,前缀和,哈希表】困难
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...

第一百八十一回 如何绘制阴影效果
文章目录 1. 概念介绍2. 使用方法2.1 SegmentedButton2.2 ButtonSegment 3. 代码与效果3.1 示例代码3.2 运行效果 4. 内容总结 1. 概念介绍 我们在本章回中介绍的SegmentedButton组件是一种分段式按钮,它把多个按钮连接成一组显示,组内再对不同的按钮进…...
Qt5.15.2静态编译 VS2017 with static OpenSSL
几年前编译过一次Qt静态库:VS2015编译Qt5.7.0生成支持XP的静态库,再次编译,毫无压力。 一.环境 系统:Windows 10 专业版 64位 编译器:visual studio 2017 第三方工具:perl,ruby和python python用最新的3.x.x版本也是可以的 这三个工具都需要添加到环境变量,安装时勾选…...
试用 13 -- 数据时效性)
AIGC(生成式AI)试用 13 -- 数据时效性
数据时效性? 最新的数据,代表最新的状态,使用最新的数据也应该最有说服力。 学习需要时间,AIGC学习并接收最新数据的效果如何? 问题很简单,如何验证?这个需要找点更新快的对像进行验证。…...

Sass的嵌套CSS 规则详细教程
文章目录 前言父选择器的标识符&群组选择器的嵌套子组合选择器和同层组合选择器:>、和~嵌套属性后言 前言 hello world欢迎来到前端的新世界 😜当前文章系列专栏:Sass和Less 🐱👓博主在前端领域还有很多知识和…...
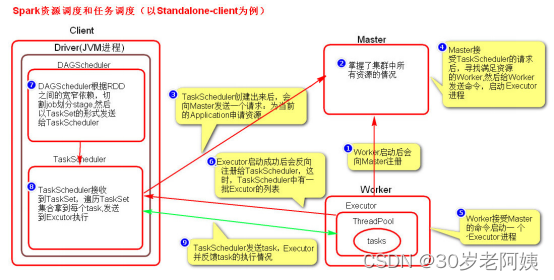
Spark---SparkCore(一)
一、术语与宽窄依赖 1、术语解释 1、Master(standalone):资源管理的主节点(进程) 2、Cluster Manager:在集群上获取资源的外部服务(例如:standalone,Mesos,Yarn) 3、Worker Node(standalone):资源管理的从节点(进程)或者说管理本机资源的…...

单链表原来是这样实现的!
文章目录 前言1. 链表的概念及结构1.1在链表里,每节“车厢”是什么样的呢?1.2为什么还需要指针变量来保存下⼀个节点的位置? 2. 单链表的实现1. 定义结构体(Seqlist)2. 打印函数(SLTPrint)小插曲,创建节点函数CreateNode3. 尾插函…...
excel一个单元格换行方法
要是在同一个单元格内输入文字输入不下的话,我们是可以进行同一个单元格换行设置的,而且换行的方法也是有很多种,下面我们就一起来看一下有哪些方法吧。 excel一个单元格换行方法: 方法一: 1、我们可以直接按下alte…...
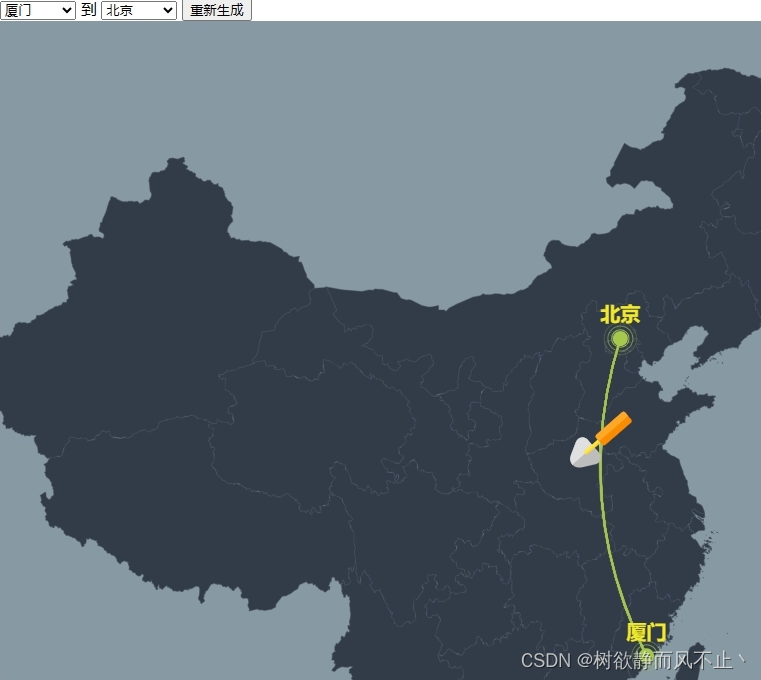
echart一键生成迁徙图
echart_move 介绍 echart迁徙图,选择起点和目的地生成迁徙图 软件架构 html echarts js 使用说明 将文件放到同一目录下打开index.html即可 默认是小飞机图标,如果想修改图标,将图片放到同一目录,如1.svg 代码修改为对应位…...

开发、测试、生产环境
开发环境:开发环境是程序猿们专门用于开发的服务器,配置可以比较随意, 为了开发调试方便,一般打开全部错误报告。简单讲就是项目尚且处于编码阶段,一般这时候会把代码放在开发环境中,不会放在生产环境中。 …...

红队攻防文库文章集锦
再救你一次,不要让欲望击溃你的意志 0.红队攻防 1.红队实战 红队攻防之特殊场景上线cs和msf CVE-2021-42287&CVE-2021-42278 域内提权 红队攻防之Goby反杀 红队攻防实战之钉钉RCE 红队攻防实战之从边界突破到漫游内网(无cs和msf) 红队攻防实战系列一之C…...

Vue框架学习笔记——键盘事件
文章目录 前文提要键盘事件(并不是所有按键都能绑定键盘事件)常用的按键不同的tab和四个按键keyCode绑定键盘事件(不推荐)Vue.config.keyCode.自定义键名 键码 神奇的猜想div标签和click.enterbutton标签和click.enter 前文提要 …...
Windows安装mysql8.0
官网地址:MySQL :: MySQL Community Downloads 选择相应版本信息下载 默认选择点击下一步 默认配置点击next 设置密码 默认配置...

Linux C++网络编程-王健伟
文章目录 1-1课程详细介绍1-2环境搭建详细介绍2-1nginx简介、选择理由、安装和使用2-2nginx整体结构、进程模型3-1学习nginx源码前的准备工作3-2nginx源码学法,终端和进程的关系说3-3信号的概念、认识、处理动作3-4Unix/Linux体系结构、信号编程初步3-5信号编程进阶…...
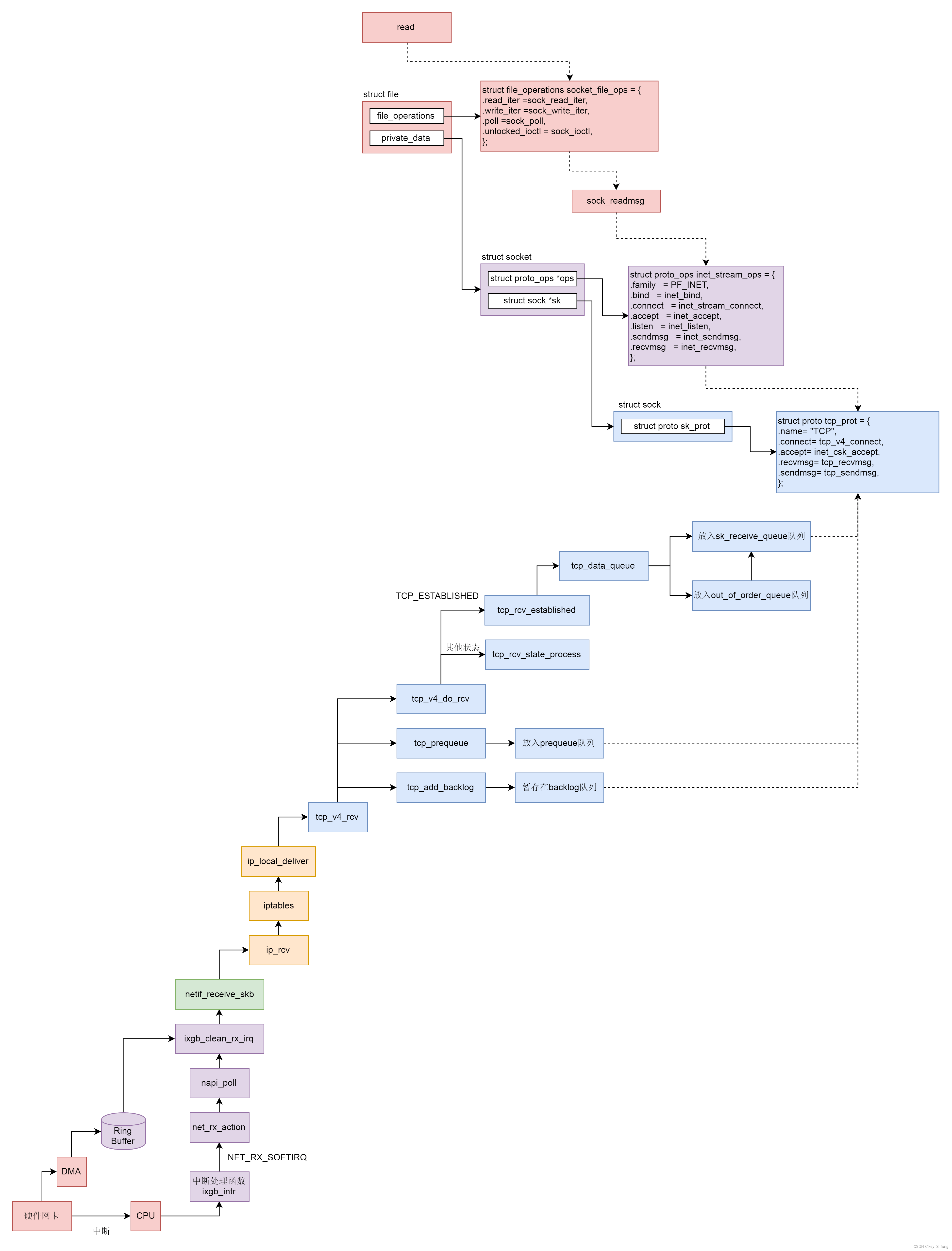
接收网络包的过程—— IP层->TCP层->Socket层
在 tcp_v4_rcv 中,得到 TCP 的头之后,我们可以开始处理 TCP 层的事情。因为 TCP 层是分状态的,状态被维护在数据结构 struct sock 里面,因而我们要根据 IP 地址以及 TCP 头里面的内容,在 tcp_hashinfo 中找到这个包对应…...

HTTP 响应头信息
HTTP 响应头信息 HTTP请求头提供了关于请求,响应或者其他的发送实体的信息。 在本章节中我们将具体来介绍HTTP响应头信息。 应答头说明Allow服务器支持哪些请求方法(如GET、POST等)。Content-Encoding文档的编码(Encode&#x…...
Android获取原始图片Bitmap的宽高大小尺寸,Kotlin
Android获取原始图片Bitmap的宽高大小尺寸,Kotlin val options BitmapFactory.Options()options.inJustDecodeBounds trueval decodeBmp BitmapFactory.decodeResource(resources, R.mipmap.p1, options)//此时,decode出来的decodeBmp宽高并不是原始图…...

数据结构之数组:简介、特性与应用
文章目录 🌾引言🌾数组的定义与特性🌿数组的定义🌿数组的特性🌿数组的优缺点 🌾数组的应用场景🍁数组的基本应用🍁动态数组(Dynamic Array)🍁多维…...
Hexo 还是 Hugo?Typecho 还是 Wordpress?读完这篇或许你就有答案了!
Hexo 首先介绍的是 Hexo,这也是咕咕没买服务器之前折腾的第一个博客。 演示站点:https://yirenliu.cn 用的主题是 butterfly,想当年刚用的时候,作者还没建群,现在 qq 群都有上千人了,GitHub 上的星星数量也有 2.7k 了。 优点 如果你不想买服务器,但也想折腾一个博客,…...

ChatGPT重磅升级!集简云支持GPT4 Turbo Vision, GPT4 Turbo, Dall.E 3,Whisper等最新模型
在11月7日凌晨,OpenAI全球开发者大会宣布了 GPT-4的一次大升级,推出了 GPT-4 Turbo号称为迄今为止最强的大模型。 此次GPT-4的更新和升级在多个方面显示出强大的优势和潜力。为了让集简云用户能快速体验新模型的能力,我们第一时间整理了大会发…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...

Elastic 获得 AWS 教育 ISV 合作伙伴资质,进一步增强教育解决方案产品组合
作者:来自 Elastic Udayasimha Theepireddy (Uday), Brian Bergholm, Marianna Jonsdottir 通过搜索 AI 和云创新推动教育领域的数字化转型。 我们非常高兴地宣布,Elastic 已获得 AWS 教育 ISV 合作伙伴资质。这一重要认证表明,Elastic 作为 …...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...
