【深度学习笔记】05 线性回归
线性回归
线性回归基于几个简单的假设:
首先,假设自变量 x \mathbf{x} x和因变量 y y y之间的关系是线性的,
即 y y y可以表示为 x \mathbf{x} x中元素的加权和,这里通常允许包含观测值的一些噪声;
其次,我们假设任何噪声都比较正常,如噪声遵循正态分布。
为了解释线性回归,我们举一个实际的例子:
我们希望根据房屋的面积(平方英尺)和房龄(年)来估算房屋价格(美元)。
为了开发一个能预测房价的模型,我们需要收集一个真实的数据集。
这个数据集包括了房屋的销售价格、面积和房龄。
在机器学习的术语中,该数据集称为训练数据集(training data set)
或训练集(training set)。
每行数据(比如一次房屋交易相对应的数据)称为样本(sample),
也可以称为数据点(data point)或数据样本(data instance)。
我们把试图预测的目标(比如预测房屋价格)称为标签(label)或目标(target)。
预测所依据的自变量(面积和房龄)称为特征(feature)或协变量(covariate)。
通常,我们使用 n n n来表示数据集中的样本数。
对索引为 i i i的样本,其输入表示为 x ( i ) = [ x 1 ( i ) , x 2 ( i ) ] ⊤ \mathbf{x}^{(i)} = [x_1^{(i)}, x_2^{(i)}]^\top x(i)=[x1(i),x2(i)]⊤,
其对应的标签是 y ( i ) y^{(i)} y(i)。
线性模型
线性假设是指目标(房屋价格)可以表示为特征(面积和房龄)的加权和,如下面的式子:
p r i c e = w a r e a ⋅ a r e a + w a g e ⋅ a g e + b . \mathrm{price} = w_{\mathrm{area}} \cdot \mathrm{area} + w_{\mathrm{age}} \cdot \mathrm{age} + b. price=warea⋅area+wage⋅age+b.
:eqlabel:eq_price-area
:eqref:eq_price-area中的 w a r e a w_{\mathrm{area}} warea和 w a g e w_{\mathrm{age}} wage
称为权重(weight),权重决定了每个特征对我们预测值的影响。
b b b称为偏置(bias)、偏移量(offset)或截距(intercept)。
偏置是指当所有特征都取值为0时,预测值应该为多少。
即使现实中不会有任何房子的面积是0或房龄正好是0年,我们仍然需要偏置项。
如果没有偏置项,我们模型的表达能力将受到限制。
严格来说, :eqref:eq_price-area是输入特征的一个
仿射变换(affine transformation)。
仿射变换的特点是通过加权和对特征进行线性变换(linear transformation),
并通过偏置项来进行平移(translation)。
给定一个数据集,我们的目标是寻找模型的权重 w \mathbf{w} w和偏置 b b b,
使得根据模型做出的预测大体符合数据里的真实价格。
输出的预测值由输入特征通过线性模型的仿射变换决定,仿射变换由所选权重和偏置确定。
而在机器学习领域,我们通常使用的是高维数据集,建模时采用线性代数表示法会比较方便。
当我们的输入包含 d d d个特征时,我们将预测结果 y ^ \hat{y} y^
(通常使用“尖角”符号表示 y y y的估计值)表示为:
y ^ = w 1 x 1 + . . . + w d x d + b . \hat{y} = w_1 x_1 + ... + w_d x_d + b. y^=w1x1+...+wdxd+b.
将所有特征放到向量 x ∈ R d \mathbf{x} \in \mathbb{R}^d x∈Rd中,
并将所有权重放到向量 w ∈ R d \mathbf{w} \in \mathbb{R}^d w∈Rd中,
我们可以用点积形式来简洁地表达模型:
y ^ = w ⊤ x + b . \hat{y} = \mathbf{w}^\top \mathbf{x} + b. y^=w⊤x+b.
:eqlabel:eq_linreg-y
在 :eqref:eq_linreg-y中,
向量 x \mathbf{x} x对应于单个数据样本的特征。
用符号表示的矩阵 X ∈ R n × d \mathbf{X} \in \mathbb{R}^{n \times d} X∈Rn×d
可以很方便地引用我们整个数据集的 n n n个样本。
其中, X \mathbf{X} X的每一行是一个样本,每一列是一种特征。
对于特征集合 X \mathbf{X} X,预测值 y ^ ∈ R n \hat{\mathbf{y}} \in \mathbb{R}^n y^∈Rn
可以通过矩阵-向量乘法表示为:
y ^ = X w + b {\hat{\mathbf{y}}} = \mathbf{X} \mathbf{w} + b y^=Xw+b
这个过程中的求和将使用广播机制。
解析解
线性回归刚好是一个很简单的优化问题。
与我们将在本书中所讲到的其他大部分模型不同,线性回归的解可以用一个公式简单地表达出来,
这类解叫作解析解(analytical solution)。
首先,我们将偏置 b b b合并到参数 w \mathbf{w} w中,合并方法是在包含所有参数的矩阵中附加一列。
我们的预测问题是最小化 ∥ y − X w ∥ 2 \|\mathbf{y} - \mathbf{X}\mathbf{w}\|^2 ∥y−Xw∥2。
这在损失平面上只有一个临界点,这个临界点对应于整个区域的损失极小点。
将损失关于 w \mathbf{w} w的导数设为0,得到解析解:
w ∗ = ( X ⊤ X ) − 1 X ⊤ y . \mathbf{w}^* = (\mathbf X^\top \mathbf X)^{-1}\mathbf X^\top \mathbf{y}. w∗=(X⊤X)−1X⊤y.
像线性回归这样的简单问题存在解析解,但并不是所有的问题都存在解析解。
解析解可以进行很好的数学分析,但解析解对问题的限制很严格,导致它无法广泛应用在深度学习里。
随机梯度下降
梯度下降最简单的用法是计算损失函数(数据集中所有样本的损失均值)
关于模型参数的导数(在这里也可以称为梯度)。
但实际中的执行可能会非常慢:因为在每一次更新参数之前,我们必须遍历整个数据集。
因此,我们通常会在每次需要计算更新的时候随机抽取一小批样本,
这种变体叫做小批量随机梯度下降(minibatch stochastic gradient descent)。
在每次迭代中,我们首先随机抽样一个小批量 B \mathcal{B} B,
它是由固定数量的训练样本组成的。
然后,我们计算小批量的平均损失关于模型参数的导数(也可以称为梯度)。
最后,我们将梯度乘以一个预先确定的正数 η \eta η,并从当前参数的值中减掉。
我们用下面的数学公式来表示这一更新过程( ∂ \partial ∂表示偏导数):
( w , b ) ← ( w , b ) − η ∣ B ∣ ∑ i ∈ B ∂ ( w , b ) l ( i ) ( w , b ) . (\mathbf{w},b) \leftarrow (\mathbf{w},b) - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \partial_{(\mathbf{w},b)} l^{(i)}(\mathbf{w},b). (w,b)←(w,b)−∣B∣ηi∈B∑∂(w,b)l(i)(w,b).
算法的步骤如下:
(1)初始化模型参数的值,如随机初始化;
(2)从数据集中随机抽取小批量样本且在负梯度的方向上更新参数,并不断迭代这一步骤。
对于平方损失和仿射变换,我们可以明确地写成如下形式:
w ← w − η ∣ B ∣ ∑ i ∈ B ∂ w l ( i ) ( w , b ) = w − η ∣ B ∣ ∑ i ∈ B x ( i ) ( w ⊤ x ( i ) + b − y ( i ) ) , b ← b − η ∣ B ∣ ∑ i ∈ B ∂ b l ( i ) ( w , b ) = b − η ∣ B ∣ ∑ i ∈ B ( w ⊤ x ( i ) + b − y ( i ) ) . \begin{aligned} \mathbf{w} &\leftarrow \mathbf{w} - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \partial_{\mathbf{w}} l^{(i)}(\mathbf{w}, b) = \mathbf{w} - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \mathbf{x}^{(i)} \left(\mathbf{w}^\top \mathbf{x}^{(i)} + b - y^{(i)}\right),\\ b &\leftarrow b - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \partial_b l^{(i)}(\mathbf{w}, b) = b - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \left(\mathbf{w}^\top \mathbf{x}^{(i)} + b - y^{(i)}\right). \end{aligned} wb←w−∣B∣ηi∈B∑∂wl(i)(w,b)=w−∣B∣ηi∈B∑x(i)(w⊤x(i)+b−y(i)),←b−∣B∣ηi∈B∑∂bl(i)(w,b)=b−∣B∣ηi∈B∑(w⊤x(i)+b−y(i)).
:eqlabel:eq_linreg_batch_update
公式 :eqref:eq_linreg_batch_update中的 w \mathbf{w} w和 x \mathbf{x} x都是向量。
∣ B ∣ |\mathcal{B}| ∣B∣表示每个小批量中的样本数,这也称为批量大小(batch size)。
η \eta η表示学习率(learning rate)。
批量大小和学习率的值通常是手动预先指定,而不是通过模型训练得到的。
这些可以调整但不在训练过程中更新的参数称为超参数(hyperparameter)。
调参(hyperparameter tuning)是选择超参数的过程。
超参数通常是我们根据训练迭代结果来调整的,
而训练迭代结果是在独立的验证数据集(validation dataset)上评估得到的。
线性回归的从零开始实现
从零开始实现整个方法,包括数据流水线、模型、损失函数和小批量随机梯度下降优化器。
%matplotlib inline
import random
import torch
from d2l import torch as d2l
生成数据集
生成一个包含1000个样本的数据集,
每个样本包含从标准正态分布中采样的2个特征。
我们的合成数据集是一个矩阵 X ∈ R 1000 × 2 \mathbf{X}\in \mathbb{R}^{1000 \times 2} X∈R1000×2。
我们使用线性模型参数 w = [ 2 , − 3.4 ] ⊤ \mathbf{w} = [2, -3.4]^\top w=[2,−3.4]⊤、 b = 4.2 b = 4.2 b=4.2
和噪声项 ϵ \epsilon ϵ生成数据集及其标签:
y = X w + b + ϵ . \mathbf{y}= \mathbf{X} \mathbf{w} + b + \mathbf\epsilon. y=Xw+b+ϵ.
ϵ \epsilon ϵ可以视为模型预测和标签时的潜在观测误差。
在这里我们认为标准假设成立,即 ϵ \epsilon ϵ服从均值为0的正态分布。
为了简化问题,我们将标准差设为0.01。
下面的代码生成合成数据集。
def synthetic_data(w, b, num_examples): #@save"""生成y=Xw+b+噪声"""X = torch.normal(0, 1, (num_examples, len(w)))y = torch.matmul(X, w) + by += torch.normal(0, 0.01, y.shape)return X, y.reshape((-1, 1))
true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = synthetic_data(true_w, true_b, 1000)
features中的每一行都包含一个二维数据样本,labels中的每一行都包含一维标签值(一个标量)
print('features:', features[0], '\nlabel:', labels[0])
features: tensor([-0.4836, -0.8441])
label: tensor([6.1063])
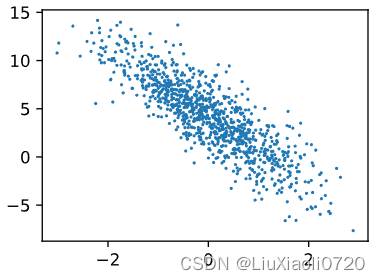
通过生成第二个特征features[:, (1)]和labels的散点图,可以直观观察到两者之间的线性关系
d2l.set_figsize()
d2l.plt.scatter(features[:, (1)].detach().numpy(), labels.detach().numpy(), 1);
读取数据集
定义一个data_iter函数,
该函数接收批量大小、特征矩阵和标签向量作为输入,生成大小为batch_size的小批量
每个小批量包含一组特征和标签。
def data_iter(batch_size, features, labels):num_examples = len(features)indices = list(range(num_examples))# 这些样本是随机读取的,没有特定的顺序random.shuffle(indices)for i in range(0, num_examples, batch_size):batch_indices = torch.tensor(indices[i: min(i + batch_size, num_examples)])yield features[batch_indices], labels[batch_indices]
读取第一个小批量数据样本并打印。
每个批量的特征维度显示批量大小和输入特征数。
同样的,批量的标签形状与batch_size相等。
batch_size = 10for X, y in data_iter(batch_size, features, labels):print(X, '\n', y)break
tensor([[ 0.3747, 0.7438],[-0.9089, -1.8827],[ 1.7131, 0.8056],[ 0.8595, 1.3511],[-1.8953, -0.4136],[-0.1327, -0.5880],[ 0.6790, -0.2707],[-0.6167, -1.1107],[-0.4787, -0.1805],[-0.5738, -0.6744]]) tensor([[2.4371],[8.7851],[4.8822],[1.3283],[1.8363],[5.9220],[6.4880],[6.7299],[3.8554],[5.3370]])
当我们运行迭代时,我们会连续地获得不同的小批量,直至遍历完整个数据集。
上面实现的迭代对教学来说很好,但它的执行效率很低,可能会在实际问题上陷入麻烦。
例如,它要求我们将所有数据加载到内存中,并执行大量的随机内存访问。
在深度学习框架中实现的内置迭代器效率要高得多,
它可以处理存储在文件中的数据和数据流提供的数据。
初始化模型参数
通过从均值为0、标准差为0.01的正态分布中采样随机数来初始化权重,
并将偏置初始化为0。
w = torch.normal(0, 0.01, size=(2, 1), requires_grad = True)
b = torch.zeros(1, requires_grad = True)
定义模型
定义模型,将模型的输入和参数同模型的输出关联起来。
要计算线性模型的输出,只需计算输入特征 X \mathbf{X} X和模型权重 w \mathbf{w} w的矩阵-向量乘法后加上偏置 b b b。
注意,上面的 X w \mathbf{Xw} Xw是一个向量,而 b b b是一个标量。
def linreg(X, w, b): #@save"""线性回归模型"""return torch.matmul(X, w) + b
定义损失函数
因为需要计算损失函数的梯度,所以我们应该先定义损失函数。
这里我们使用平方损失函数。
在实现中,我们需要将真实值y的形状转换为和预测值y_hat的形状相同。
def squared_loss(y_hat, y): #@save"""均方损失"""return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2
定义优化算法
在每一步中,使用从数据集中随机抽取的一个小批量,然后根据参数计算损失的梯度。
接下来,朝着减少损失的方向更新我们的参数。
下面的函数实现小批量随机梯度下降更新。
该函数接受模型参数集合、学习速率和批量大小作为输入。每
一步更新的大小由学习速率lr决定。
因为我们计算的损失是一个批量样本的总和,所以我们用批量大小(batch_size)
来规范化步长,这样步长大小就不会取决于我们对批量大小的选择。
def sgd(params, lr, batch_size): #@save"""小批量随机梯度下降"""with torch.no_grad():for param in params:param -= lr * param.grad / batch_sizeparam.grad.zero_()
训练
在每次迭代中,我们读取一小批量训练样本,并通过我们的模型来获得一组预测。
计算完损失后,我们开始反向传播,存储每个参数的梯度。
最后,我们调用优化算法sgd来更新模型参数。
概括一下,我们将执行以下循环:
- 初始化参数
- 重复以下训练,直到完成
- 计算梯度 g ← ∂ ( w , b ) 1 ∣ B ∣ ∑ i ∈ B l ( x ( i ) , y ( i ) , w , b ) \mathbf{g} \leftarrow \partial_{(\mathbf{w},b)} \frac{1}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} l(\mathbf{x}^{(i)}, y^{(i)}, \mathbf{w}, b) g←∂(w,b)∣B∣1∑i∈Bl(x(i),y(i),w,b)
- 更新参数 ( w , b ) ← ( w , b ) − η g (\mathbf{w}, b) \leftarrow (\mathbf{w}, b) - \eta \mathbf{g} (w,b)←(w,b)−ηg
在每个迭代周期(epoch)中,我们使用data_iter函数遍历整个数据集,
并将训练数据集中所有样本都使用一次(假设样本数能够被批量大小整除)。
这里的迭代周期个数num_epochs和学习率lr都是超参数,分别设为3和0.03。
lr = 0.03
num_epochs = 3
net = linreg
loss = squared_loss
for epoch in range(num_epochs):for X, y in data_iter(batch_size, features, labels):l = loss(net(X, w, b), y) # X和y的小批量损失# 因为l形状是(batch_size,1),而不是一个标量。l中的所有元素被加到一起,# 并以此计算关于[w,b]的梯度l.sum().backward()sgd([w, b], lr, batch_size) # 使用参数的梯度更新参数with torch.no_grad():train_l = loss(net(features, w, b), labels)print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')
epoch 1, loss 0.041500
epoch 2, loss 0.000147
epoch 3, loss 0.000047
print(f'w的估计误差: {true_w - w.reshape(true_w.shape)}')
print(f'b的估计误差: {true_b - b}')
w的估计误差: tensor([ 0.0002, -0.0003], grad_fn=<SubBackward0>)
b的估计误差: tensor([0.0002], grad_fn=<RsubBackward1>)
线性回归的简洁实现
使用PyTorch框架来实现线性回归模型
生成数据集
import numpy as np
import torch
from torch.utils import data
from d2l import torch as d2l
true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = d2l.synthetic_data(true_w, true_b, 1000)
读取数据集
调用框架中现有的API来读取数据。将features和labels作为API的参数传递,并通过数据迭代器指定batch_size。此外,布尔值is_train表示是否希望数据迭代器对象在每个迭代周期内打乱数据。
def load_array(data_arrays, batch_size, is_train=True): #@save"""构造一个PyTorch数据迭代器"""dataset = data.TensorDataset(*data_arrays)return data.DataLoader(dataset, batch_size, shuffle=is_train)
batch_size = 10
data_iter = load_array((features, labels), batch_size)
为了验证是否正常工作,读取并打印第一个小批量样本。
使用iter构造Python迭代器,并使用next从迭代器中获取第一项。
next(iter(data_iter))
[tensor([[ 0.3532, -0.6057],[ 1.6997, -1.6114],[ 1.3135, 3.0438],[-1.0064, -1.3555],[ 1.6724, 0.7461],[ 0.3855, -1.5162],[ 0.7502, 0.5924],[ 0.8864, -0.1364],[ 2.0878, -2.4125],[ 0.4963, 1.4179]]),tensor([[ 6.9696],[13.0706],[-3.5134],[ 6.7924],[ 5.0087],[10.1182],[ 3.6684],[ 6.4485],[16.5720],[ 0.3795]])]
定义模型
对于标准深度学习模型,可以使用框架的预定义好的层。
首先定义一个模型变量net,它是一个Sequential类的实例。
Sequential类将多个层串联在一起。当给定输入数据时,Sequential实例将数据传入到第一层,然后将第一层的输出作为第二层的输入,以此类推。
在PyTorch中,全连接层在Linear类中定义。值得注意的是,我们将两个参数传递到nn.Linear中,第一个指定输入特征形状,即2,第二个指定输出特征形状,输出特征形状为单个标量,因此为1。
# nn是神经网络的缩写
from torch import nnnet = nn.Sequential(nn.Linear(2, 1))
初始化模型参数
在使用net之前,需要初始化模型参数。
深度学习框架通常有预定义的方法来初始化参数。在这里指定每个权重参数应该从均值为0、标准差为0.01的正态分布中随机采样,偏置参数将初始化为零。
正如在构造nn.Linear时指定输入和输出尺寸一样,现在能直接访问参数以设定它们的初始值。通过net[0]选择网络中的第一个图层,然后使用weight.data和bias.data方法访问参数。还可以使用替换方法normal_和fill_来重写参数值。
net[0].weight.data.normal_(0, 0.01)
net[0].bias.data.fill_(0)
tensor([0.])
定义损失函数
计算均方误差使用的是MSELoss类,也成为平方 L 2 L_{2} L2范数。
默认情况下,它返回所有样本损失的平均值。
loss = nn.MSELoss()
定义优化算法
小批量随机梯度下降算法是一种优化神经网络的标准工具,
PyTorch在optim模块中实现了该算法的许多变种。
当我们(实例化一个SGD实例)时,我们要指定优化的参数
(可通过net.parameters()从我们的模型中获得)以及优化算法所需的超参数字典。
小批量随机梯度下降只需要设置lr值,这里设置为0.03。
trainer = torch.optim.SGD(net.parameters(), lr = 0.03)
训练
在每个迭代周期里,将完整遍历一次数据集(train_data),
不停地从中获取一个小批量的输入和相应的标签。
对于每一个小批量,会进行以下步骤:
- 通过调用
net(X)生成预测并计算损失l(前向传播)。 - 通过进行反向传播来计算梯度。
- 通过调用优化器来更新模型参数。
为了更好的衡量训练效果,计算每个迭代周期后的损失,并打印它来监控训练过程。
num_epochs = 3
for epoch in range(num_epochs):for X, y in data_iter:l = loss(net(X), y)trainer.zero_grad()l.backward()trainer.step()l = loss(net(features), labels)print(f'epoch {epoch + 1}, loss {1:f}')
epoch 1, loss 1.000000
epoch 2, loss 1.000000
epoch 3, loss 1.000000
比较生成数据集的真实参数和通过有限数据训练获得的模型参数
w = net[0].weight.data
print('w的估计误差:', true_w - w.reshape(true_w.shape))
b = net[0].bias.data
print('b的估计误差:', true_b - b)
w的估计误差: tensor([-0.0001, 0.0005])
b的估计误差: tensor([-0.0008])
相关文章:

【深度学习笔记】05 线性回归
线性回归 线性回归基于几个简单的假设: 首先,假设自变量 x \mathbf{x} x和因变量 y y y之间的关系是线性的, 即 y y y可以表示为 x \mathbf{x} x中元素的加权和,这里通常允许包含观测值的一些噪声; 其次,我…...

二叉树算法—后继节点
与其明天开始,不如现在行动! 文章目录 1 后继节点1.1 解题思路1.2 代码实现 💎总结 1 后继节点 1.1 解题思路 二叉树节点结构定义如下: public static class Node { public int cal; public Node left; public Node right; public…...

C语言做一个恶作剧关机程序
一、项目介绍 C语言实现一个简单的"流氓软件",一个可以强制关机恶作剧关机程序,输入指定指令可以解除 二、运行截图 然后当你输入“n”才可以解锁关机。 三、完整源码 #include <stdlib.h> #include <stdio.h> #include <s…...
数据结构 / 计算机内存分配
1. Linux 32位系统内存分配 栈(stack): 先进后出, 栈区变量先定义的后分配内存, 栈区地址从高到低分配堆(heap): 先进先出, 栈区变量先定义的先分配内存, 堆区地址从低到高分配堆栈溢出: 表示的是栈区内存耗尽, 称为溢出. 例如: 每次调用递归都需要在栈区申请内存, 如果递归太深…...

计算机视觉算法——基于Transformer的目标检测(DN DETR / DINO / Sparser DETR / Lite DETR)
计算机视觉算法——基于Transformer的目标检测(DN DETR / DINO) 计算机视觉算法——基于Transformer的目标检测(DN DETR / DINO)1. DN DETR1.1 Stablize Hungarian Matching1.2 Denoising1.3 Attention Mask 2. DINO2.1 Contrasti…...
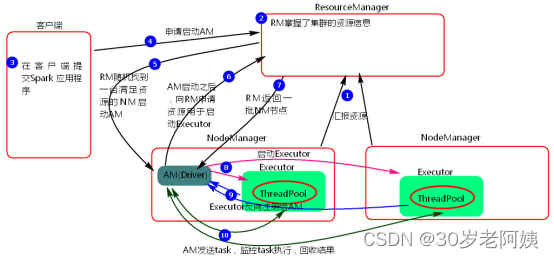
Spark---基于Yarn模式提交任务
Yarn模式两种提交任务方式 一、yarn-client提交任务方式 1、提交命令 ./spark-submit --master yarn --class org.apache.spark.examples.SparkPi ../examples/jars/spark-examples_2.11-2.3.1.jar 100 或者 ./spark-submit --master yarn–client --class org.apache.s…...

SpringCloud之Gateway(统一网关)
文章目录 前言一、搭建网关服务1、导入依赖2、在application.yml中写配置 二、路由断言工厂Route Predicate Factory三、路由过滤器 GatewayFilter案例1给所有进入userservice的请求添加一个请求头总结 四、全局过滤器 GlobalFilter定义全局过滤器,拦截并判断用户身…...
案例029:基于微信小程序的阅读网站设计与实现
文末获取源码 开发语言:Java 框架:SSM JDK版本:JDK1.8 数据库:mysql 5.7 开发软件:eclipse/myeclipse/idea Maven包:Maven3.5.4 小程序框架:uniapp 小程序开发软件:HBuilder X 小程序…...

27. Spring源码篇之SpEL表达式之自定义解析模版
简介 其实前面文章我们已经介绍过了如何定义spring表达式的解析模版,但是那是直接使用表达式api的形式,对于使用spring的同学来说,更优雅的方式就是可以自定义一个扩展去修改 本文就是介绍如何通过Spring的扩展点修改表达式解析模版 自定义…...
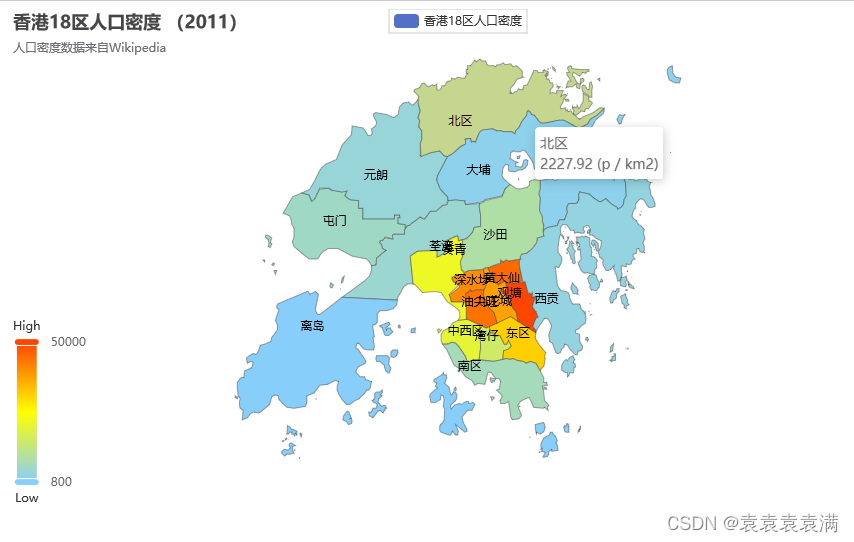
100天精通Python(可视化篇)——第109天:Pyecharts绘制各种常用地图(参数说明+代码实战)
文章目录 专栏导读一、地图应用场景二、参数说明1. 导包2. add函数 三、地图绘制实战1. 省市地图2. 中国地图3. 中国地图(带城市)4. 中国地图(分段型)5. 中国地图(连续型)6. 世界地图7. 行程轨迹地图8. 人口…...
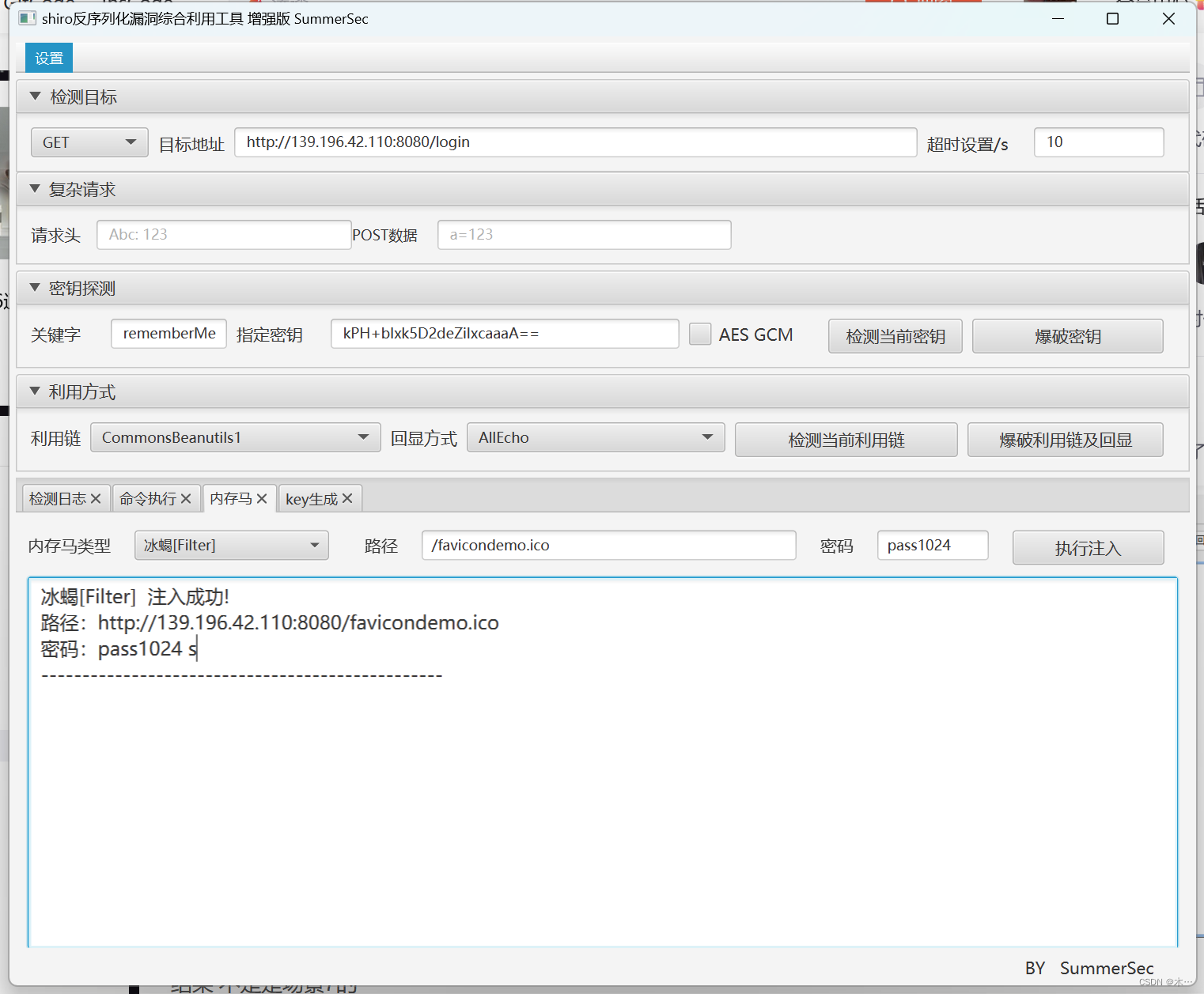
bugku 渗透测试
场景1 查看源代码 场景2 用dirsearch扫描一下看看 ok看到登录的照应了第一个提示 进去看看 不出所料 随便试试admin/admin进去了 在基本设置里面看到falg 场景3 确实是没啥想法了 找到php在线运行 检查网络,我们发现这个php在线运行会写入文件 那我们是不是写…...

WordPress用sql命令批量删除所有文章
有时我们需要将一个网站搬迁到另一个服务器。我们只想保留网站的模板样式,而不需要文章内容。一般情况下我们可以在后台删除已发表的文章,但如果有很多文章,我们则需要一次删除所有文章。 WordPress如何批量删除所有文章 进入网站空间后台&a…...

树状数组 / pbds解法 E2. Array Optimization by Deque
Problem - 1579E2 - Codeforces Array Optimization by Deque - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 树状数组解法 将 a i a_i ai插入到队头,贡献为:原队列中所有比 a i a_i ai小的数的数量将 a i a_i ai插入到队尾,贡献为&a…...

原神「神铸赋形」活动祈愿现已开启
亲爱的旅行者,「神铸赋形」活动祈愿现已开启,「单手剑静水流涌之辉」「法器碧落之珑」概率UP! 活动期间,旅行者可以在「神铸赋形」活动祈愿中获得更多武器与角色,提升队伍的战斗力! 〓祈愿时间〓 4.2版本更…...

php使用Session实现简单购物车功能
一个简单的商城购物车功能。它使用了PHP的会话(Session)来存储购物车数据,通过调用不同的函数来实现添加商品、移除商品、更新商品数量以及清空购物车的功能 session_start();// 初始化购物车 if (!isset($_SESSION[cart])) {$_SESSION[cart] array(); }// 添加商品…...
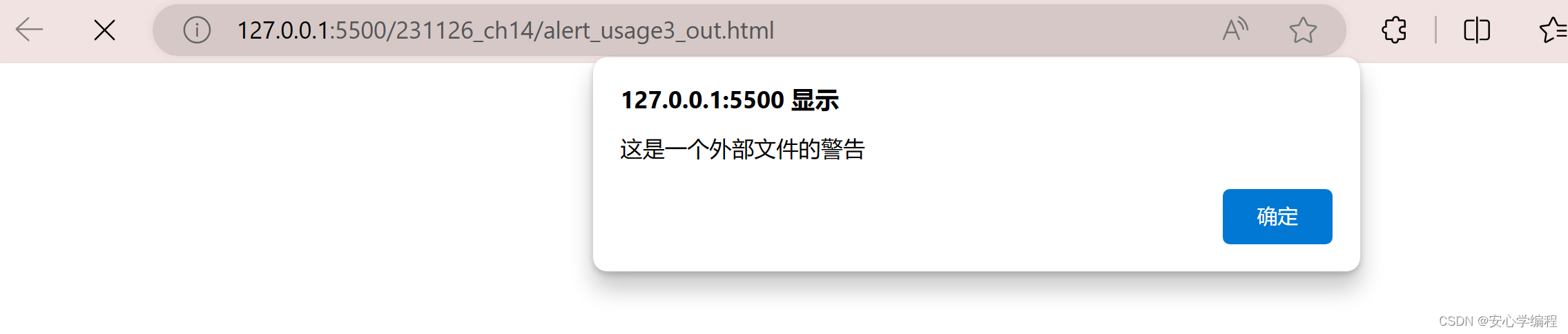
【JavaScript】alert的使用方法 | 超详细
alert作用效果 alert()方法用于显示带有一条指定消息和一个确认的按钮的警告框。 alert使用方法 方法一:直接写在script标签内 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"&…...

总结Vue3里一些常见的组合式api
一:前言 二:常见api 1、ref 和 reactive 这两个组合式 api 是在 Vue3 开发中最为常见的两个 api ,主要是将一个非响应式的数据变为响应式数据。 ref作用: 定义一个数据的响应式 语法: const xxx ref(initValue):创建一个包含响应式数据的引…...

C_5练习题
一、单项选择题(本大题共20小题,每小题2分,共40分。在每小题给出的四个备选项中,选出一个正确的答案,并将所选项前的字母填写在答题纸的相应位置上。) 1.以下不正确的C语言标识符是() A. AB1 B._ab3 C. char D. a2_b 若 x、i、j、k都是 int型变量&#…...
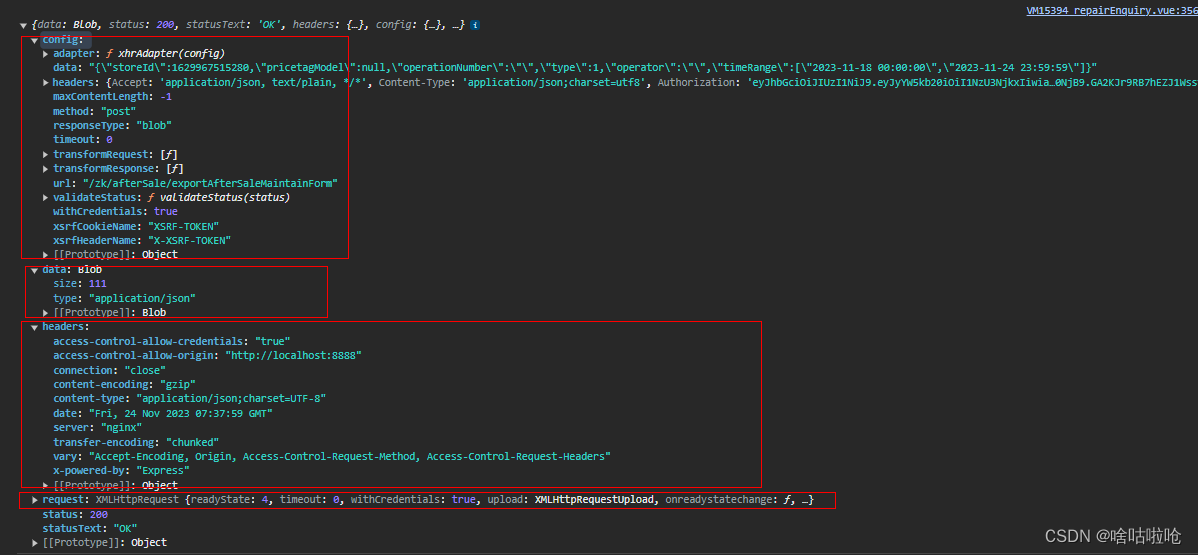
【采坑分享】导出文件流responseType:“blob“如何提示报错信息
目录 前言: 采坑之路 总结: 前言: 近日,项目中踩了一个坑分享一下经验,也避免下次遇到方便解决。项目基于vue2axioselement-ui,业务中导出按钮需要直接下载接口中的文件流。正常是没有问题,但…...
机器学习算法——主成分分析(PCA)
目录 1. 主体思想2. 算法流程3. 代码实践 1. 主体思想 主成分分析(Principal Component Analysis)常用于实现数据降维,它通过线性变换将高维数据映射到低维空间,使得映射后的数据具有最大的方差。主成分可以理解成数据集中的特征…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...
