机器学习算法——主成分分析(PCA)
目录
- 1. 主体思想
- 2. 算法流程
- 3. 代码实践
1. 主体思想
主成分分析(Principal Component Analysis)常用于实现数据降维,它通过线性变换将高维数据映射到低维空间,使得映射后的数据具有最大的方差。主成分可以理解成数据集中的特征,具体来说,第一主成分是数据中方差最大的特征(即该特征下的值的方差最大),数据点在该方向有最大的扩散性(即在该方向上包含的信息量最多)。第二主成分与第一主成分正交(即与第一主成分无关),并在所有可能正交方向中,选择方差次大的方向。然后,第三主成分与前两个主成分正交,且选择在其余所有可能正交方向中有最大方差的方向,以此类推,有多少特征就有多少主成分。
- 主成分上的方差越小,说明该特征上的取值可能都相同,那这一个特征的取值对样本而言就没有意义,因为其包含的信息量较少。
- 主成分上的方差越大,说明该特征上的值越分散,那么它包含的信息就越多,对数据降维就越有帮助。
下图1中,紫色线方向上数据的方差最大(该方向上点的分布最分散,包含了更多的信息量),则可以将该方向上的特征作为第一主成分。

主成分分析的优点2:
- 数据降维:PCA能够减少数据的维度(复杂度),提高计算效率。
- 数据可视化:通过PCA降维,可以将数据可视化到更低维度的空间中,便于数据的观察和理解。
- 去除噪声: 主成分分析可以把数据的主要特征提取出来(数据的主要特征集中在少数几个主成分上),忽略小的、可能是噪声的特征,同时可以防止过拟合。
- 去除冗余: 在原始数据中,很多情况下多个变量之间存在高度相关性,导致数据冗余。PCA通过新的一组正交的主成分来描述数据,可以最大程度降低原始的数据冗余。
2. 算法流程
- 数据预处理:中心化 x i − x ˉ x_i-\bar{x} xi−xˉ (每列的每个值都减去该列的均值)。
- 求样本的协方差矩阵 1 m X T X \frac{1}{m}X^TX m1XTX(m为样本数量,X为样本矩阵)。
- 计算协方差矩阵的特征值和对应的特征向量。
- 选择最大的 K K K 个特征值对应的 K K K 个特征向量构造特征矩阵。
- 将中心化后的数据投影到特征矩阵上。
- 输出投影后的数据集。
协方差矩阵的计算(二维)
C = 1 m X T X = ( C o v ( x , x ) C o v ( x , y ) C o v ( y , x ) C o v ( y , y ) ) = ( 1 m ∑ i = 1 m x i 2 1 m ∑ i = 1 m x i y i 1 m ∑ i = 1 m y i x i 1 m ∑ i = 1 m y i 2 ) C=\frac{1}{m}X^TX=\begin{pmatrix}Cov(x,x)&Cov(x,y) \\Cov(y,x)&Cov(y,y)\end{pmatrix} =\begin{pmatrix} \frac{1}{m}\sum_{i=1}^{m}x_i^2&\frac{1}{m}\sum_{i=1}^{m}x_iy_i \\ \frac{1}{m}\sum_{i=1}^{m}y_ix_i&\frac{1}{m}\sum_{i=1}^{m}y_i^2 \end{pmatrix} C=m1XTX=(Cov(x,x)Cov(y,x)Cov(x,y)Cov(y,y))=(m1∑i=1mxi2m1∑i=1myixim1∑i=1mxiyim1∑i=1myi2)
其中, x x x 和 y y y 表示不同的特征列, c o v ( x , x ) = D ( x ) = 1 m ∑ i = 1 m ( x i − x ˉ ) 2 cov(x,x)=D(x)=\frac{1}{m}\sum_{i=1}^{m}(x_i-\bar{x})^2 cov(x,x)=D(x)=m1∑i=1m(xi−xˉ)2(协方差矩阵中的 x i x_i xi 表示已经中心化后的值),协方差矩阵是一个对称的矩阵,且对角线元素是各个特征(一列即为一个特征)的方差。
协方差矩阵的计算(三维)
C = ( C o v ( x , x ) C o v ( x , y ) C o v ( x , z ) C o v ( y , x ) C o v ( y , y ) C o v ( y , z ) C o v ( z , x ) C o v ( z , y ) C o v ( z , z ) ) C=\begin{pmatrix} Cov(x,x)&Cov(x,y)&Cov(x,z) \\ Cov(y,x)&Cov(y,y)&Cov(y,z) \\ Cov(z,x)&Cov(z,y)&Cov(z,z) \end{pmatrix} C= Cov(x,x)Cov(y,x)Cov(z,x)Cov(x,y)Cov(y,y)Cov(z,y)Cov(x,z)Cov(y,z)Cov(z,z)
举例说明
下面共5个样本,每个样本两个特征,第一列的均值为2.2,第二列的均值为3.8。
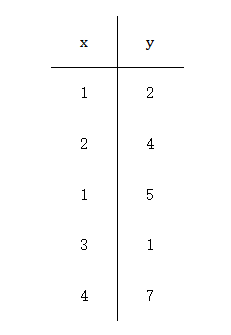
-
数据中心化(每列的每个值都减去该列的均值)

-
计算协方差矩阵
C = [ 1.7 1.05 1.05 5.7 ] C=\begin{bmatrix} 1.7&1.05 \\ 1.05&5.7 \end{bmatrix} C=[1.71.051.055.7] -
计算特征值与特征向量
e i g e n v a l u e s = [ 1.4411286 , 5.9588714 ] eigenvalues=[1.4411286,5.9588714] eigenvalues=[1.4411286,5.9588714]
e i g e n v e c t o r s = [ − 0.97092685 − 0.23937637 0.23937637 − 0.97092685 ] eigenvectors=\begin{bmatrix} -0.97092685&-0.23937637\\ 0.23937637&-0.97092685 \end{bmatrix} eigenvectors=[−0.970926850.23937637−0.23937637−0.97092685] -
选择最大的一个特征值(将数据降为一维)5.9588714,对应的特征向量为
[ − 0.23937637 − 0.97092685 ] \begin{bmatrix} -0.23937637\\ -0.97092685 \end{bmatrix} [−0.23937637−0.97092685] -
将中心化后的数据投影到特征矩阵
[ − 1.2 − 1.8 − 0.2 0.2 − 1.2 1.2 0.8 − 2.8 1.8 3.2 ] ∗ [ − 0.23937637 − 0.97092685 ] = [ 2.03491998 − 0.1463101 − 0.87786057 2.52709409 − 3.5378434 ] \begin{bmatrix} -1.2&-1.8 \\ -0.2&0.2 \\ -1.2&1.2 \\ 0.8&-2.8 \\ 1.8&3.2 \end{bmatrix}*\begin{bmatrix} -0.23937637\\ -0.97092685 \end{bmatrix}=\begin{bmatrix} 2.03491998\\ -0.1463101\\ -0.87786057\\ 2.52709409\\ -3.5378434 \end{bmatrix} −1.2−0.2−1.20.81.8−1.80.21.2−2.83.2 ∗[−0.23937637−0.97092685]= 2.03491998−0.1463101−0.877860572.52709409−3.5378434
[ 2.03491998 − 0.1463101 − 0.87786057 2.52709409 − 3.5378434 ] \begin{bmatrix} 2.03491998\\ -0.1463101\\ -0.87786057\\ 2.52709409\\ -3.5378434 \end{bmatrix} 2.03491998−0.1463101−0.877860572.52709409−3.5378434 即为降维后的数据。
3. 代码实践
from sklearn.neural_network import MLPClassifier
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report,confusion_matrix
import numpy as np
import matplotlib.pyplot as plt# 载入手写体数据集并切分为训练集和测试集
digits = load_digits()
x_data = digits.data
y_data = digits.target
x_train, x_test, y_train, y_test = train_test_split(x_data,y_data)
x_data.shape
运行结果
(1797, 64)
# 创建神经网络模型,包含两个隐藏层,每个隐藏层的神经元数量分别为
# 100和50,最大迭代次数为500
mlp = MLPClassifier(hidden_layer_sizes=(100,50) ,max_iter=500)
mlp.fit(x_train,y_train)
# 数据中心化
def zeroMean(dataMat):# 按列求平均,即各个特征的平均meanVal = np.mean(dataMat, axis=0) newData = dataMat - meanValreturn newData, meanVal# PCA降维,top表示要将数据降维到几维
def pca(dataMat,top):# 数据中心化newData,meanVal=zeroMean(dataMat) # np.cov用于求协方差矩阵,参数rowvar=0说明数据一行代表一个样本covMat = np.cov(newData, rowvar=0)# np.linalg.eig求矩阵的特征值和特征向量eigVals, eigVects = np.linalg.eig(np.mat(covMat))# 对特征值从小到大排序eigValIndice = np.argsort(eigVals)# 从eigValIndice中提取倒数top个索引,并按照从大到小的顺序返回一个切片列表# 后一个 -1 表示切片的方向为从后往前,以负的步长(-1)进行迭代n_eigValIndice = eigValIndice[-1:-(top+1):-1]# 最大的n个特征值对应的特征向量n_eigVect = eigVects[:,n_eigValIndice]# 低维特征空间的数据lowDDataMat = newData*n_eigVect# 利用低纬度数据来重构数据reconMat = (lowDDataMat*n_eigVect.T) + meanVal# 返回低维特征空间的数据和重构的矩阵return lowDDataMat,reconMat
# 绘制降维后的数据及分类结果,共10个类
lowDDataMat, reconMat = pca(x_data, 2)
predictions = mlp.predict(x_data)
x = np.array(lowDDataMat)[:,0]
y = np.array(lowDDataMat)[:,1]
plt.scatter(x,y,c=y_data)
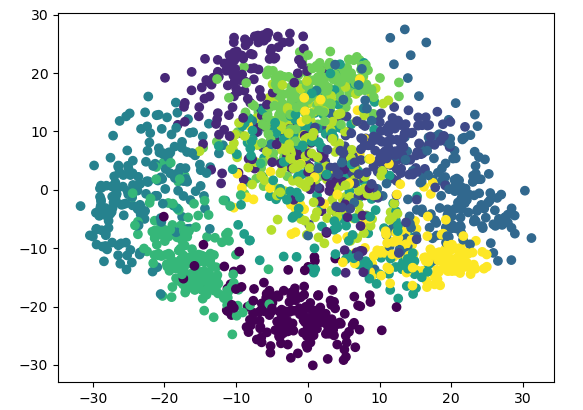
# 将数据降为3维
lowDDataMat, reconMat = pca(x_data,3)
# 绘制三维数据及分类结果,共10个类
x = np.array(lowDDataMat)[:,0]
y = np.array(lowDDataMat)[:,1]
z = np.array(lowDDataMat)[:,2]
ax = plt.figure().add_subplot(111, projection = '3d')
ax.scatter(x, y, z, c = y_data, s = 10) #点为红色三角形
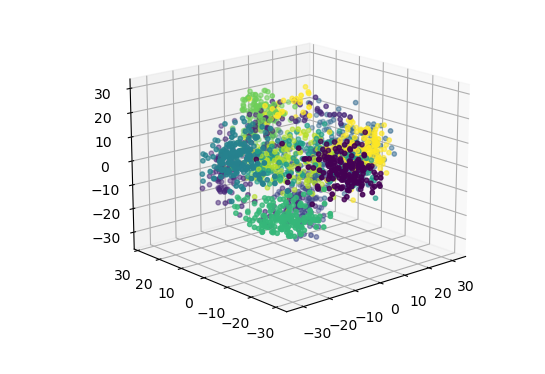
主成分分析(PCA) ↩︎
主成分分析(PCA)理解 ↩︎
相关文章:

机器学习算法——主成分分析(PCA)
目录 1. 主体思想2. 算法流程3. 代码实践 1. 主体思想 主成分分析(Principal Component Analysis)常用于实现数据降维,它通过线性变换将高维数据映射到低维空间,使得映射后的数据具有最大的方差。主成分可以理解成数据集中的特征…...
01、copilot+pycharm
之——free for student 目录 之——free for student 杂谈 正文 1.for student 2.pycharm 3.使用 杂谈 copilot是github推出的AI程序员,将chatgpt搬到了私人终端且无token限制,下面是使用方法。 GitHub Copilot 是由 GitHub 与 OpenAI 合作开发的…...

一般将来时
一般将来时 概念 表示将要发生的动作或打算、计划准备做某事 时间 tomorrow 明天 the day after tomorrow 后天 next week 下周 next weekend 下周末 next month 下个月 next year 明年 ...句子结构 主语 be(am/is/are)going to do … 计划,…...
【古诗生成AI实战】之四——模型包装器与模型的训练
在上一篇博客中,我们已经利用任务加载器task成功地从数据集文件中加载了文本数据,并通过预处理器processor构建了词典和编码器。在这一过程中,我们还完成了词向量的提取。 接下来的步骤涉及到定义模型、加载数据,并开始训练过程。…...

redis实现消息延迟队列
业务场景 在很多软件系统功能中都会出现定时任务的业务场景,比如提前点单,比如定时发布动态,文章等而出现这样的的定时的任务为延迟队任务 代码模块 任务的持久化一般都需要建立一个任务表和任务日志表,避免宕机导致任务失效,先新建立一个数据库,创建基本的任务表和任务日志表…...

keyof
// 在TypeScript中,keyof是一个操作符, // 它允许你从一个类型中提取所有的可枚举属性名,并将它们组成一个联合类型。 // 例如,假设你有这样一个类型: type Person { firstName: string; lastName: string; age: n…...

Centos 7 更改 PostgreSQL 14 默认存储路径
前言: 默认PostgreSQL数据存储路径为:/var/lib/pgsql/14/data 迁移到新的存储路径:/mnt/postgresql/data 1、关闭PostgreSQL服务 systemctl stop postgresql-142、创建目录 # 创建新目录 mkdir -p /mnt/postgresql/data# 更改目录权限 chow…...
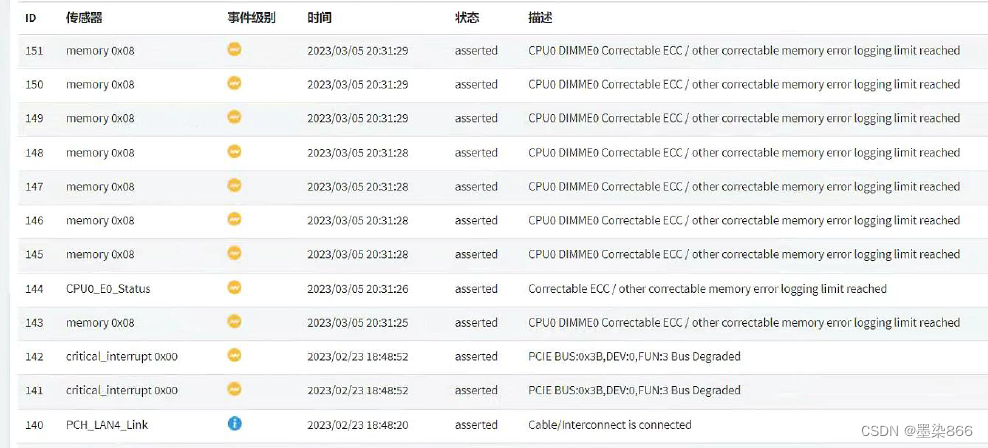
深信服超融合一体机提示:内存ECC
PS:此事件分享主要来源于季度巡检时发现的超融合一体机红灯闪烁异常,接入IPMI端口查看日志发现持续提示内存ECC; 因为是只有3.05这一天发现了有这个告警的提示,所以当时清除了日志以后重启了BMC服务就解决了;但是如果清…...

STK Components 二次开发-地面站传感器
上一篇我们说了创建地面站,那么这次我们在地面站添加一些特效。 1. 创建地面站 var locationPoint1 new PointCartographic(m_earth, new Cartographic(Trig.DegreesToRadians(117.17066), Trig.DegreesToRadians(31.84056), 240.359)); m_facility new Platfor…...
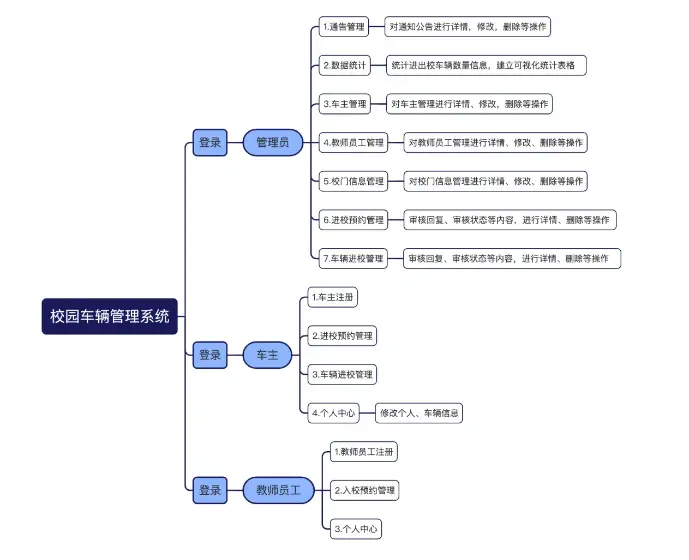
基于springboot校园车辆管理系统
背景 伴随着社会经济的快速发展,机动车保有量不断增加。不断提高的大众生活水平以及人们不断增长的自主出行需求,人们对汽车的 依赖性在不断增强。汽车已经发展成为公众日常出行的一种重要的交通工具。在如此形势下,高校校园内的机动车数量也…...
通用电气调查网络攻击和数据盗窃指控
通用电气正在调查有关威胁行为者在网络攻击中破坏了公司开发环境并泄露据称被盗数据的指控。 通用电气 (GE) 是一家美国跨国公司,业务涉及电力、可再生能源和航空航天行业。 本月早些时候,一个名为 IntelBroker 的威胁行为者试图在黑客论坛上以 500 美…...

2023亚太赛数学建模A题:采果机器人的图像识别技术思路模型代码
亚太A题:采果机器人的图像识别技术 A题完整思路获取 :获取见文末名片,第一时间更新 中国是世界上最大的苹果生产国,年产量约为3500万吨。与此同时,中国也是世 界上最大的苹果出口国,全球每两个苹果中就有…...

C++ 协程
经典协程辅助入门代码: typedef cotask::task my_task_t; int main() { // create a task using factory function [with lambda expression] my_task_t::ptr_t task my_task_t::create([]() { //创建协程 std::cout ()->get_id() cotask::this_task::get…...
EventBus的使用)
Flutter学习(六)EventBus的使用
背景 项目开发过程中,有些场景,需要跨页面进行数据传递。按照安卓开发的思路,在flutter实现一个事件总线EventBus,进行数据传递 原理 通过dart的签名函数,进行监听集合设置,然后post分发的时候ÿ…...

Linux系统---僵尸进程、孤儿进程
顾得泉:个人主页 个人专栏:《Linux操作系统》 《C/C》 键盘敲烂,年薪百万! 有了上一篇博客的学习,我们已经简单了解了进程的基础知识,今天我们再来学习两个特殊的进程,僵尸进程和孤儿进程。 …...

SpringBoot中如何优雅地使用重试
1 缘起 项目中使用了第三方的服务, 第三方服务偶尔会出现不稳定、连接不上的情况, 于是,在调用时为了保证服务的相对高可用,添加了超时连接重试, 当连接第三方服务超时时,多重试几次,比如3次&a…...

数据库日志解析:深入了解MySQL中的各类日志
**> 🎏:你只管努力,剩下的交给时间 🏠 :小破站 数据库日志解析:深入了解MySQL中的各类日志 前言第一:错误日志❌1. 错误日志的作用2. 记录内容3. 故障排查的方法 第二:查询日志1.…...

操作系统题目分类总结 | 进程管理 内存管理 文件系统 设备管理
系列文章如下 学习过程中一定要有系统观念(知识框架,每一章开头都会有一个思维导图),知道目前自己在学习的是哪一板块的内容,和前面有什么样的联系 操作系统的很多知识点前后都是联系非常紧密的,去一点一…...
数据结构——单链表(Singly Linked List)
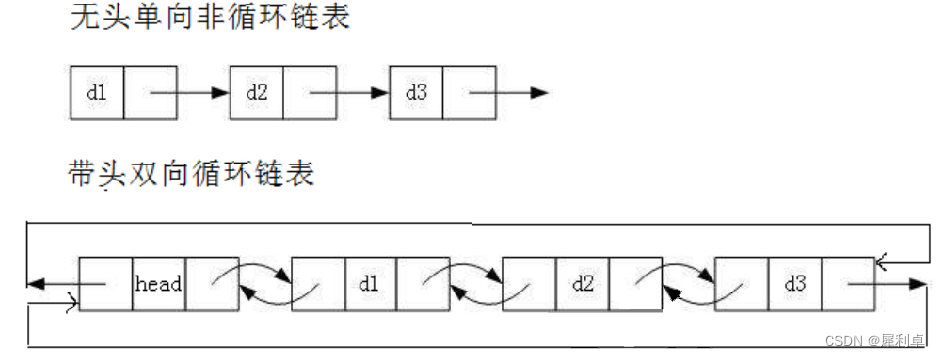
1.链表介绍 链表是一种物理储存上非连续、非顺序的存储结构。数据元素的逻辑顺序是通过链表中的指针链接次序实现的。链表由一系列结点(链表中每一个元素称为结点)组成,结点可以在运行时动态生成。 对于上图,每一个结点都是一个结…...

4面试题--数据库(补充)
隔离性问题 若不考虑隔离性则会出现以下问题 1. 脏读:指⼀个事务在处理数据的过程中,读取到另⼀个 未提交 事务的数据 2. 不可重复读:指对于数据库中的某个数据(同⼀个数据项),⼀个事务内的多次查询却…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...

DiscuzX3.5发帖json api
参考文章:PHP实现独立Discuz站外发帖(直连操作数据库)_discuz 发帖api-CSDN博客 简单改造了一下,适配我自己的需求 有一个站点存在多个采集站,我想通过主站拿标题,采集站拿内容 使用到的sql如下 CREATE TABLE pre_forum_post_…...
