C#,《小白学程序》第二十课:大数的加法(BigInteger Add)

大数的(加减乘除)四则运算、阶乘运算。
乘法计算包括小学生算法、Karatsuba和Toom-Cook3算法。
重复了部分 19 课的代码。
1 文本格式
using System;
using System.Linq;
using System.Text;
using System.Collections.Generic;
/// <summary>
/// 大数的(加减乘除)四则运算、阶乘运算
/// 乘法计算包括小学生算法、Karatsuba和Toom-Cook3算法
/// </summary>
public static class BigInteger_Utility
{
/// <summary>
/// 记录 加减乘除 的运算次数
/// </summary>
public static int[] operations { get; set; } = new int[] { 0, 0, 0, 0 };
/// <summary>
/// 《小白学程序》第十九课:随机数(Random)第六,随机生成任意长度的大数(BigInteger)
/// 一般可将超过9位数的数字成为“大数”。
/// 两个大数之间的四则运算用于密码学、高精度计算等应用。
/// 位数很多的浮点数可转为大数,再逆转即可。
/// </summary>
/// <param name="n"></param>
/// <returns></returns>
public static string rand(int n)
{
// 随机数发生器
Random rnd = new Random();
StringBuilder sb = new StringBuilder();
// 第一个数字不能为0,故:0-8之间的随机数+ 1 = 1-9
sb.Append((rnd.Next(9) + 1).ToString());
// 后面 n-1 个数字为 0-9;从 1 开始计数
for (int i = 1; i < n; i++)
{
sb.Append((rnd.Next(10)).ToString());
}
return sb.ToString();
}
/// <summary>
/// 字符串型的数字转为数组
/// 低位(右)在前,比如 "123" , n=6 存为 3,2,1,_,_,_
/// n 可能大于 a 的长度;剩余位置留出来用于 进位 等。
/// </summary>
/// <param name="a"></param>
/// <param name="n">最大位数,后面留0</param>
/// <returns></returns>
public static int[] string_to_digitals(string a, int n)
{
// 字符串 转为 “字符数组”
char[] c = a.ToCharArray();
// 存储数字的数组
int[] d = new int[n];
// 从最右端(个位)数字开始,转存为数字数组,参与后面的计算
for (int i = a.Length - 1, j = 0; i >= 0; i--)
{
// 跳过数字前面可能有的 - 号
if (a[i] == '-') continue;
// '0' 字符是最小的数字字符
// 数值 = 字符 - '0' ;
d[j++] = a[i] - '0';
}
return d;
}
/// <summary>
/// 数组型数字转为字符串型
/// 低位(右)在前,比如 3,2,1,_,_,_ 转为 "123", n=6
/// 这是前面 string_to_digitals 的反向计算函数
/// n 可能大于 d 的长度;剩余位置留出来用于 进位 等。
/// </summary>
/// <param name="d"></param>
/// <returns></returns>
public static string digitals_to_string(int[] d)
{
int n = d.Length;
// 数字数组 d 含有一些无效的数组;
// 因此,先从最右段开始去除无效的位置
int k = n - 1;
//for (; (k >= 0) && (d[k] == 0); k--) ;
while ((k >= 0) && (d[k] == 0)) k--;
// 找到有效位置后,开始组合字符串;
if (k >= 0)
{
StringBuilder sb = new StringBuilder();
for (; k >= 0; k--) sb.Append(d[k]);
return sb.ToString();
}
else
{
return "0";
}
}
/// <summary>
/// 《小白学程序》第二十课:大数(BigInteger)的四则运算之一,加法
/// 大数加法 c = a + b
/// </summary>
/// <param name="a"></param>
/// <param name="b"></param>
/// <returns></returns>
public static string big_integer_plus(string a, string b)
{
int n = Math.Max(a.Length, b.Length) + 1;
// 位数不长的数字直接计算
if (n <= 18)
{
return (ulong.Parse(a) + ulong.Parse(b)).ToString();
}
int[] da = string_to_digitals(a, n);
int[] db = string_to_digitals(b, n);
// 从低位(右)往高位(左)相加
#if _ORIGINAL__
for (int i = 0; i < (n - 1); i++)
{
da[i] += db[i];
if (da[i] > 9)
{
da[i] -= 10;
da[i + 1] += 1;
}
}
return digitals_to_string(da);
#else
int[] dc = new int[n];
Array.Copy(da, dc, n);
for (int i = 0; i < (n - 1); i++)
{
dc[i] = dc[i] + db[i];
if (dc[i] > 9)
{
dc[i] -= 10;
dc[i + 1] += 1;
}
}
return digitals_to_string(dc);
#endif
}
}
2 代码格式
using System;
using System.Linq;
using System.Text;
using System.Collections.Generic;/// <summary>
/// 大数的(加减乘除)四则运算、阶乘运算
/// 乘法计算包括小学生算法、Karatsuba和Toom-Cook3算法
/// 除法运算为 Truffer 自创算法;
/// </summary>
public static class BigInteger_Utility
{/// <summary>/// 记录 加减乘除 的运算次数/// </summary>public static int[] operations { get; set; } = new int[] { 0, 0, 0, 0 };/// <summary>/// 《小白学程序》第十九课:随机数(Random)第六,随机生成任意长度的大数(BigInteger)/// 一般可将超过9位数的数字成为“大数”。/// 两个大数之间的四则运算用于密码学、高精度计算等应用。/// 位数很多的浮点数可转为大数,再逆转即可。/// </summary>/// <param name="n"></param>/// <returns></returns>public static string rand(int n){// 随机数发生器Random rnd = new Random();StringBuilder sb = new StringBuilder();// 第一个数字不能为0,故:0-8之间的随机数+ 1 = 1-9sb.Append((rnd.Next(9) + 1).ToString());// 后面 n-1 个数字为 0-9;从 1 开始计数for (int i = 1; i < n; i++){sb.Append((rnd.Next(10)).ToString());}return sb.ToString();}/// <summary>/// 字符串型的数字转为数组/// 低位(右)在前,比如 "123" , n=6 存为 3,2,1,_,_,_/// n 可能大于 a 的长度;剩余位置留出来用于 进位 等。/// </summary>/// <param name="a"></param>/// <param name="n">最大位数,后面留0</param>/// <returns></returns>public static int[] string_to_digitals(string a, int n){// 字符串 转为 “字符数组”char[] c = a.ToCharArray();// 存储数字的数组int[] d = new int[n];// 从最右端(个位)数字开始,转存为数字数组,参与后面的计算for (int i = a.Length - 1, j = 0; i >= 0; i--){// 跳过数字前面可能有的 - 号if (a[i] == '-') continue;// '0' 字符是最小的数字字符// 数值 = 字符 - '0' ;d[j++] = a[i] - '0';}return d;}/// <summary>/// 数组型数字转为字符串型/// 低位(右)在前,比如 3,2,1,_,_,_ 转为 "123", n=6/// 这是前面 string_to_digitals 的反向计算函数/// n 可能大于 d 的长度;剩余位置留出来用于 进位 等。/// </summary>/// <param name="d"></param>/// <returns></returns>public static string digitals_to_string(int[] d){int n = d.Length;// 数字数组 d 含有一些无效的数组;// 因此,先从最右段开始去除无效的位置int k = n - 1;//for (; (k >= 0) && (d[k] == 0); k--) ;while ((k >= 0) && (d[k] == 0)) k--;// 找到有效位置后,开始组合字符串;if (k >= 0){StringBuilder sb = new StringBuilder();for (; k >= 0; k--) sb.Append(d[k]);return sb.ToString();}else{return "0";}}/// <summary>/// 《小白学程序》第二十课:大数(BigInteger)的四则运算之一,加法/// 大数加法 c = a + b/// </summary>/// <param name="a"></param>/// <param name="b"></param>/// <returns></returns>public static string big_integer_plus(string a, string b){int n = Math.Max(a.Length, b.Length) + 1;// 位数不长的数字直接计算if (n <= 18){return (ulong.Parse(a) + ulong.Parse(b)).ToString();}int[] da = string_to_digitals(a, n);int[] db = string_to_digitals(b, n);// 从低位(右)往高位(左)相加
#if _ORIGINAL__for (int i = 0; i < (n - 1); i++){da[i] += db[i];if (da[i] > 9){da[i] -= 10;da[i + 1] += 1;}}return digitals_to_string(da);
#elseint[] dc = new int[n];Array.Copy(da, dc, n);for (int i = 0; i < (n - 1); i++){dc[i] = dc[i] + db[i];if (dc[i] > 9){dc[i] -= 10;dc[i + 1] += 1;}}return digitals_to_string(dc);
#endif}
}
3 计算结果
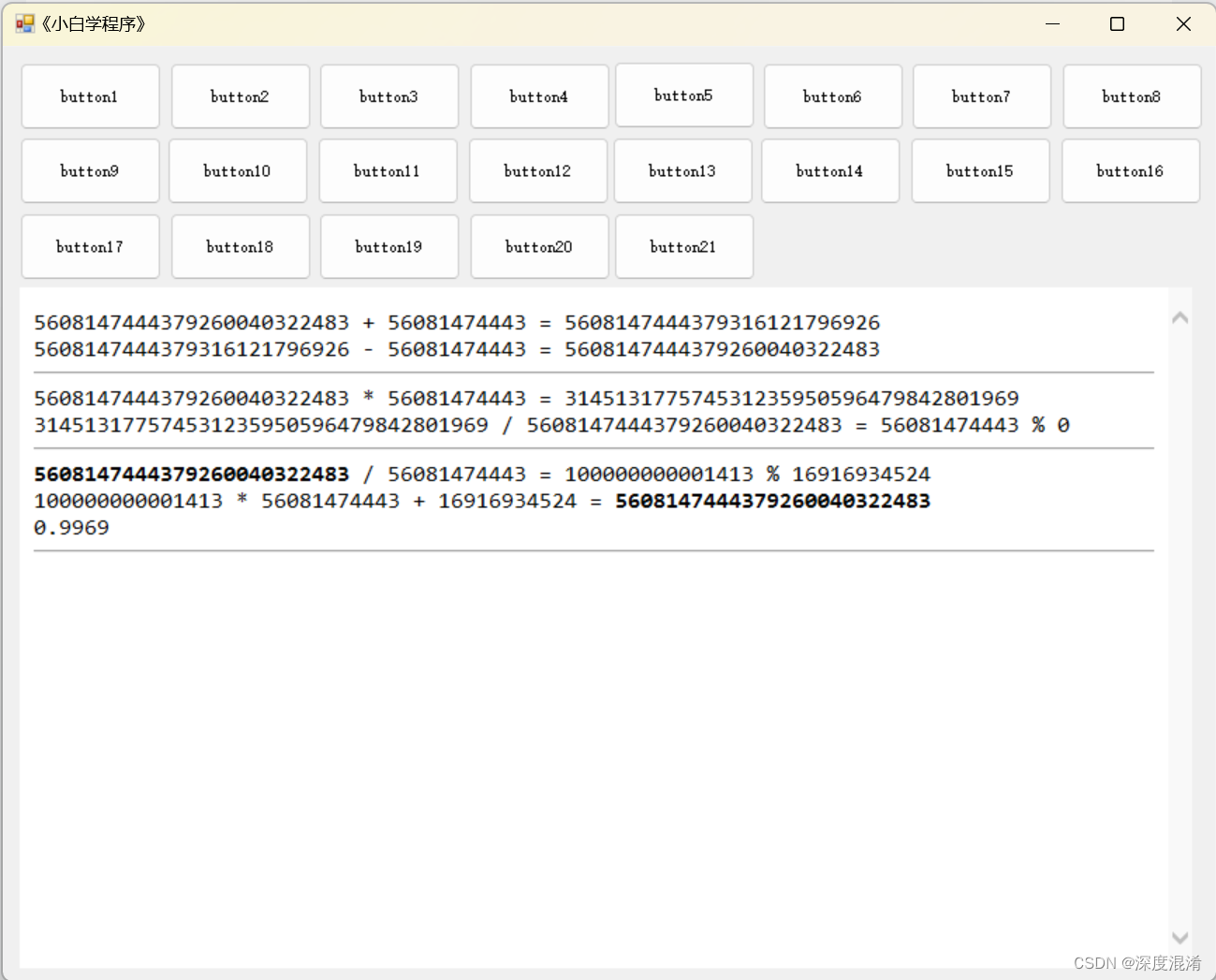
相关文章:

C#,《小白学程序》第二十课:大数的加法(BigInteger Add)
大数的(加减乘除)四则运算、阶乘运算。 乘法计算包括小学生算法、Karatsuba和Toom-Cook3算法。 重复了部分 19 课的代码。 1 文本格式 using System; using System.Linq; using System.Text; using System.Collections.Generic; /// <summary>…...

通用功能——git 攻略
摘要 本文主要介绍git常用命令的使用方法,同时介绍一些常见问题的处理方法,持续更新中… git命令通用选项 大多数git命令都适用的选项列表如下: -v, --verbose show hash and subject, give twice for upstream branch -q, --quie…...
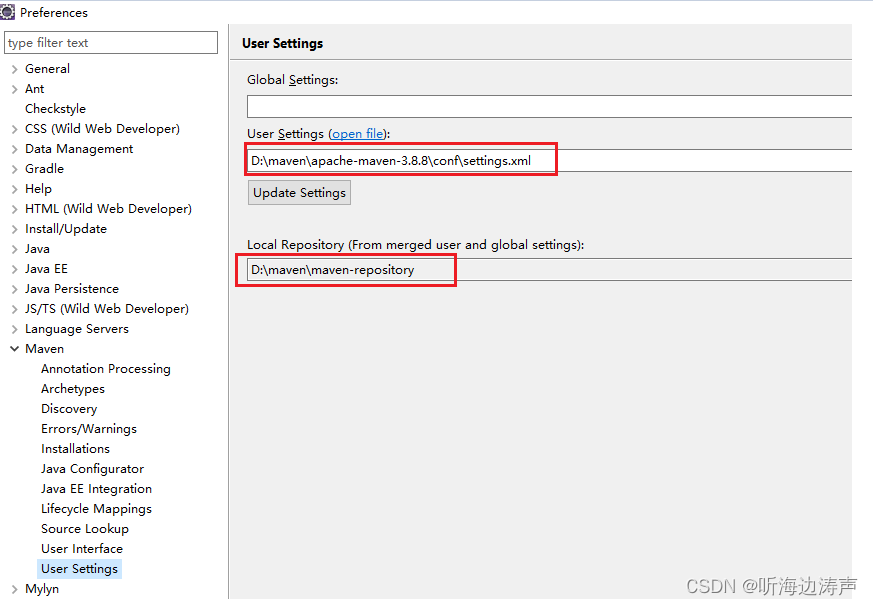
LemMinX-Maven:帮助在eclipse中更方便地编辑maven的pom文件
LemMinX-Maven:https://github.com/eclipse/lemminx-maven LemMinX-Maven可以帮助我们在eclipse中更方便地编辑maven工程的pom.xml文件,例如补全、提示等。不用单独安装,因为在安装maven eclipse插件的时候已经自动安装了: 例…...

CAD与 PDM系统如何协同工作的?
在产品研发中,CAD(计算机辅助设计)和PDM(产品数据管理)是两个核心的工具,它们在产品从设计到制造的整个生命周期中发挥着重要的作用。虽然这两个工具在功能上有所不同,但它们在使用上却有着密切…...

vue-历史模式部署
项目部署 本项目采用nginx进行部署,历史模式的部署需要服务端的配合,本次采用nginx进行配合。 1 配置 const basePath process.env.VUE_APP_BASE_PATH; module.exports {publicPath: basePath #静态资源的路径 /ecology/ }2 创建路由 const createR…...

『Linux升级路』基础开发工具——make/Makefile
🔥博客主页:小王又困了 📚系列专栏:Linux 🌟人之为学,不日近则日退 ❤️感谢大家点赞👍收藏⭐评论✍️ 目录 一、认识make/Makefile 📒1.1make/Makefile的优点 📒…...
Python开发技能实战-如何在Visio中添加和删除任意连接点?
问题 在学习或者工作中,我们经常会借助Visio这个软件绘制流程图,在Visio中一般连接点是固定的,固定的连接点只能绘制一条连接线,如下图所示: 但有时候我们需要在两个方框之间绘制双向连接线,达到以下的效果…...

中科驭数受邀出席2023 ODCC冬季全会,共谋开放数据中心创新发展
近日,2023年开放数据中心委员会(简称“ODCC”)冬季全会在宁夏银川成功召开,中科驭数作为ODCC的新成员单位,受邀出席本次重要会议。 ▲ 中科驭数正式加入ODCC开放数据中心委员会 开放数据中心委员会是在中国通信标准化…...

Leetcode—907.子数组的最小值之和【中等】
2023每日刷题(四十二) Leetcode—907.子数组的最小值之和 算法思想 参考自y神思想 实现代码 class Solution { public:int sumSubarrayMins(vector<int>& arr) {long long ans 0;const int mod 1e97;int n arr.size();stack<int>…...

下载文件并重命名
//下载文件并重命名 // 无需数字化归档模版下载 function nodigitalMeth(){ let filenameunescape("/projectapp/ghsjy/template/noNeedDigital.docx")//原文件为英文名字 downloadFileRename(filename,"无需成果数据汇交模版") } // 需要数字化归档模版下…...
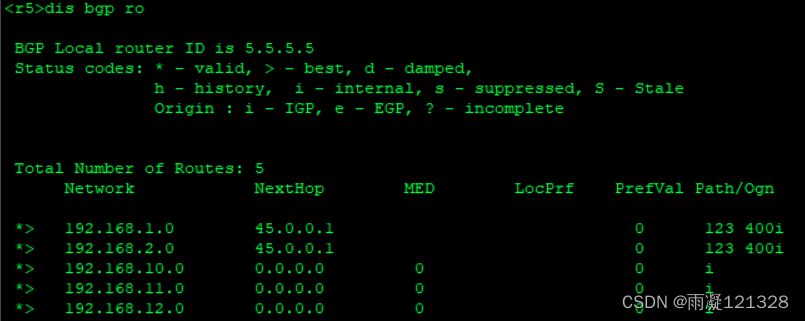
BGP路由的选路综合实验
题目要求 1.使用PreVal策略,确保R1通过R3到达192.168.10.0/24 2.使用AS_Path策略,确保R1通过R3到达192.168.11.0/24 3.配置MED策略,确保R1通过R3到达192.168.12.0/24 4.使用Local Preference策略,确保R4通过R2到达192.168.1.0/24…...

英语语法:连词or, and, if, unless怎么用?
连词or, and, if, unless怎么用?1. or conj. 或者,还是, 和, 否则用法:并列连词①当“或者,还是”讲时,用在选择疑问句中,是选择疑问句的标志例:Are you a teacher or a …...

基于Spring、SpringMVC、MyBatis的闪烁物业管理系统
文章目录 项目介绍主要功能截图:部分代码展示设计总结项目获取方式🍅 作者主页:超级无敌暴龙战士塔塔开 🍅 简介:Java领域优质创作者🏆、 简历模板、学习资料、面试题库【关注我,都给你】 🍅文末获取源码联系🍅 项目介绍 基于SSM的闪烁物业管理系统,java项目。 …...
uni-app 离线打包安卓Apk(小白上手)
场景: 在使用uni-app 开发apk时,使用云打包有次数限制。尤其对于测试阶段是无比难受的,通常是浪费打包次数进行打包或者通过usb 给测试机更新开发环境,但这都是无比漫长的过程 尤其有多个测试机真的是噩梦般的存在 下载离线打包示…...

fatal: refusing to merge unrelated histories報錯咋辦
在 Git 中,如果要合并两个分支,而这两个分支的历史记录不相交,就会出现错误:fatal: refusing to merge unrelated histories。 要解决这个问题,有以下几种方法: 首先,检查一下你正在合并的两个…...

第二十二章 解读pycocotools的API,目标检测mAP的计算COCO的评价指标(工具)
Pycocotools介绍 为使用户更好地使用 COCO数据集, COCO 提供了各种 API。COCO是一个大型的图像数据集,用于目标检测、分割、人的关键点检测、素材分割和标题生成。这个包提供了Matlab、Python和luaapi,这些api有助于在COCO中加载、解析和可视化注释。 …...

如何避免光模块接口受到污染?
光模块作为光通信领域一个重要的配件,实现光电和电光的转换,和光纤连接,承载了数据流量的快速转换与传输。因而在整个网络体系中,起着至关重要的作用。虽然光模块在使用过程中,不像交换机和服务器等网络设备一样需要经…...

虚拟机系列:Oracle VM VirtualBox虚拟机的使用教程和使用体验情况反馈
Oracle VM VirtualBox虚拟机的使用教程和使用体验情况反馈 一. 简述:二. 下载三. 安装解压后选择需要的版本点击安装1:第一步,点击安装,点击下一步2. 这里直接点击下一步,3. 网络警告选择:是4. 准备好以后,点击安装5. 点击完成即可四. 打开五. 创建虚拟机1. 输入虚拟机名…...

echarts 通用线性渐变堆叠面积图
echarts 通用线性渐变堆叠面积图 getLineData2() {const myChart echarts.init(this.$refs.chartDom);const option {tooltip: {trigger: axis,},legend: {show: false,textStyle: {fontSize: 14, //字体大小color: #ffffff, //字体颜色},data: [AAA, BBB],},grid: {show: tr…...
在云服务器上搭建个人版chatGPT及后端Spring Boot集成chat GPT
原创/朱季谦 本文分成两部分,包括【国内服务器上搭建chat GPT】和【后端Spring Boot集成chat GPT】。 无论是在【国内服务器上搭建chat GPT】和【后端Spring Boot集成chat GPT】,两个方式都需要魔法访问,否则是无法正常使用的,即…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...
