计算机缺少d3dx9_43.dll怎么办?5个方法快速修复d3dx9_43.dll文件
在计算机使用过程中,我们常常会遇到一些错误提示,其中之一就是“d3dx9_43.dll丢失”。这个问题可能会影响到我们的游戏体验或者软件运行。为了解决这个问题,我查阅了一些资料并尝试了多种方法。在这里,我想分享一下我对d3dx9_43.dll丢失问题的解决方法以及其原因的介绍。
首先,让我们了解一下d3dx9_43.dll丢失的原因。这个文件是DirectX的一个组件,它负责处理游戏中的一些特效和图形渲染。当这个文件丢失或损坏时,游戏或其他需要使用DirectX的软件就无法正常运行,从而出现错误提示。
那么,如何解决d3dx9_43.dll丢失的问题呢?以下是我总结的五个解决方法:

1. 重新安装DirectX:
我们可以从微软官网下载最新版本的DirectX安装包,然后按照提示进行安装。安装完成后,重新启动计算机。

2. 使用DLL修复工具程序(已使用可以解决):
使用dll修复工具,一种专门用于修复损坏或缺失的动态链接库dll文件的软件,直接在网上下载一个dll修复工具,当然网上的dll修复工具是五花八门的,很容易下载到垃圾的软件。
可以在浏览器顶部输入:dll修复文件.site(按下键盘回车键打开)这样子安全可靠。(亲测可修复)

下载完成解压打开,打开工具后,点击“扫描并修复”,等待扫描完成并修复问题。,dll修复工具还可以帮助您修复 电脑其它未知dll 文件丢失问题,并确保应用程序可以正常运行。只需要耐心等待修复完成,提示修复完成重启电脑即能解决dll丢失问题。

3. 从其他计算机上复制d3dx9_43.dll文件:
如果我们有其他安装了相同版本的DirectX的计算机,可以从那里复制d3dx9_43.dll文件。找到文件后,将其复制到我们出现问题的计算机上的相应目录中。

4. 更新显卡驱动程序:
有时候,d3dx9_43.dll丢失的问题可能是由于显卡驱动程序不兼容或损坏导致的。我们可以从显卡制造商的官网下载最新的驱动程序,然后安装并重启计算机。这样可能会解决问题。

5. 系统还原:
如果以上方法都无法解决问题,我们还可以尝试使用系统还原功能。通过还原到之前没有问题的时间点,可以恢复到一个没有d3dx9_43.dll丢失的状态。但是需要注意的是,系统还原可能会导致我们丢失一些最近的更改和数据。
总的来说,d3dx9_43.dll丢失是一个常见的问题,但通过一些简单的方法就可以解决。希望我的分享能够帮助到遇到类似问题的人们,让大家能够更好地享受计算机带来的乐趣。同时,我也希望能够将这些知识分享给其他人,帮助他们更好地解决类似的问题。
相关文章:

计算机缺少d3dx9_43.dll怎么办?5个方法快速修复d3dx9_43.dll文件
在计算机使用过程中,我们常常会遇到一些错误提示,其中之一就是“d3dx9_43.dll丢失”。这个问题可能会影响到我们的游戏体验或者软件运行。为了解决这个问题,我查阅了一些资料并尝试了多种方法。在这里,我想分享一下我对d3dx9_43.d…...
2023亚太杯数学建模C题思路分析 - 我国新能源电动汽车的发展趋势
1 赛题 问题C 我国新能源电动汽车的发展趋势 新能源汽车是指以先进技术原理、新技术、新结构的非常规汽车燃料为动力来源( 非常规汽车燃料指汽油、柴油以外的燃料),将先进技术进行汽车动力控制和驱动相结 合的汽车。新能源汽车主要包括四种类型&#x…...

c语言新龟兔赛跑
以下是一个使用C语言编写的新的龟兔赛跑游戏: #include <stdio.h>#include <stdlib.h>#include <time.h>int main() { int distance, turtle_speed, rabbit_speed, turtle_time, rabbit_time, rabbit_lead; srand(time(NULL)); // 随机数种…...
Linux驱动开发——网络设备驱动(理论篇)
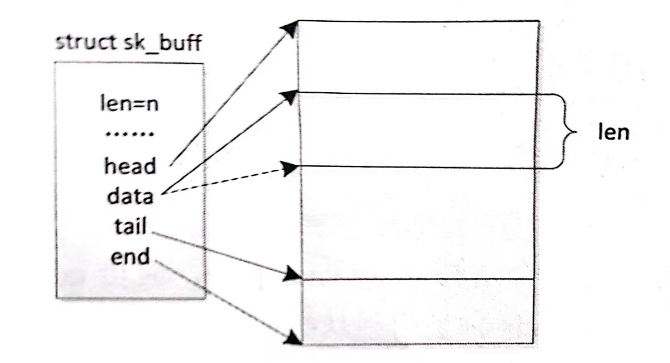
目录 一、前言 二、网络层次结构 三、网络设备驱动核心数据结构和函数 一、前言 网络设备驱动是 Linux 的第三大类驱动,也是我们学习的最后一类 Linux 驱动。这里我们首先简单学习一下网络协议层次结构,然后简单讨论 Linux 内核中网络实现的层次结构。…...

simulink仿真
1)系统问题 连续系统,离散系统(采样周期问题) 系统分析问题 2)求解器问题 变步长,定步长,步长时间与采样周期问题、 3)积分器问题 连续积分,离散积分问题ÿ…...
PC端页面进去先出现加载效果
自定义指令v-loading,只需要绑定Boolean即可 v-loading“loading” <el-table :data"list" border style"width: 100%" v-loading"loading"><el-table-column align"center" label"序号" width"5…...
磁盘清理在哪里?学会这4个方法,快速清理内存!
“在使用电脑的过程中,我可能经常会保存一些文件到电脑上,这也导致电脑经常出现内存不足的情况。我想问问磁盘清理在哪里呀?我应该如何打开呢?” 随着使用电脑的时间增长,用户可能经常会遇到磁盘空间不足的情况&#x…...
Error opening terminal: xterm.”的解决方法
主要是看下面这两个变量是否设置正确 $ echo $TERM $ echo $TERMINFO 通常TERM的默认值为xterm-265color, 要查看支持的term,可以ls -al /lib/terminfo/x/ 如果TERM是xterm-265color的话,TERMINFO设置为/usr/lib/terminfo make menuconfig时提示“Err…...

C#常见的设计模式-结构型模式
引言 设计模式是软件工程中用于解决常见问题的可复用解决方案。在C#编程中,常见的设计模式具有广泛的应用。本篇博客将重点介绍C#中常见的结构型设计模式,包括适配器模式、装饰器模式、代理模式、组合模式和享元模式。 目录 引言1. 适配器模式(Adapter …...

Redis分片备库切换操作
Redis分片备库切换操作 场景描述: 分片集群: 1.ipa:5001-ipa:5002 2.ipb:5001-ipb:5002 需将两个分片备库互置完成灾备 操作步骤 准备工作 主机密码:1qaz!QAZ 获取节点信息命令 /redispath/bin/redis-cli -a password -h ip -p port red…...
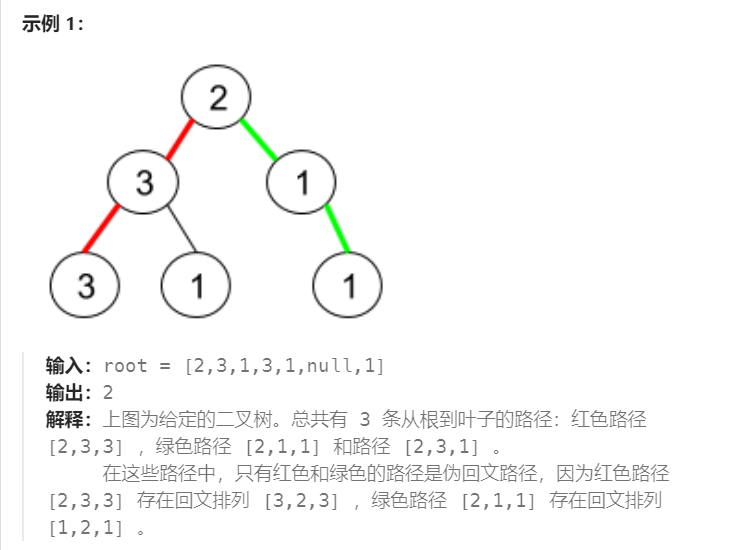
二叉树:leetcode1457. 二叉树中的伪回文路径
给你一棵二叉树,每个节点的值为 1 到 9 。我们称二叉树中的一条路径是 「伪回文」的,当它满足:路径经过的所有节点值的排列中,存在一个回文序列。 请你返回从根到叶子节点的所有路径中 伪回文 路径的数目。 给定二叉树的节点数目…...
【【Linux下的Petallinux 以及其他的配置】】
Linux下的Petallinux 以及其他的配置 sudo apt-get install iproute2 gawk python3 python build-essential gcc git make net-tools libncurses5-dev tftpd zlib1g-dev libssl-dev flex bison libselinux1 gnupg wget git-core diffstat chrpath socat xterm autoconf libtoo…...

13、深度学习之神经网络
深度学习是机器学习中重要的一个学科分支,它的特点就在于需要构建多层“深度”的神经网络。 人们在探索人工智能初期,就曾设想构建一个用数学方式来表达的模型,它可以模拟人的大脑,大脑我们都知道,有很多神经元,每个神经元之间通过突触链接。 神经网络的设计就是模仿了这…...

js的数组去重方法
目录 es6数组中对象去重 1. filter()用法 2. findIndex()用法 3. 去重 其他方法: 方法二:reduce()去重 1. reduce()用法 1.1 找出字符长度最长的数组成员。 1.2 扁平化二维数组 1.3 扁平化多维数组 三、总结方案: 使用Set…...

在 Next 14 的 appRouter 模式中接入 React-Redux
在 Next 14 的 appRouter 模式中接入 React-Redux 说明 Next.js 版本升级到 14 后,相比 13 版本是一个改动很大的大版本升级,很多概念或者使用方式 13 版本都有较大的区别,因此这里记录一些学习 14 版本的 Next.js 的心得体会或者问题。因为…...

aspose-words 跳过证书验证jar
优先用 aspose-words-19.3.jar ,不需要读取license.xml,导出后直接水印,jar包最好直接放在项目resource目录下直接引用,要不下载不下来 public static String doc2pdf(String fileName, String filePath) {try {String oldFile f…...

【开题报告】基于uniapp的瑜伽学习交流小程序的设计与实现
1.选题背景 瑜伽在现代社会中越来越受到人们的关注和喜爱。它不仅可以帮助人们塑造健美的身材,还能促进身心健康、提高生活质量。然而,由于瑜伽动作的复杂性和技巧性,很多初学者在学习过程中会遇到困难和挑战。 同时,由于工作和…...
)
【蓝桥杯单片机】应用手势传感器(串口2)
手势传感器:串口通信,可以识别左滑、右滑、单击三种手势,输出相应的固定串口数据。 控制器:IAP15F2K61S2单片机。 引脚连接: 单片机 手势传感器 P46 -> TX P47 -> RX VCC -> 5V GND->gnd main.c 程序说明:传感器与单片机的串口2进行数据交互,这里使用的是开…...

51单片机蜂鸣器发出悦耳的声音
51单片机蜂鸣器发出悦耳的声音 1.概述 这篇文章介绍单片机控制蜂鸣器入门小实验,通过该实验掌握蜂鸣器发声的原理,控制声音发出我们想听的音乐。 2.蜂鸣器发声 2.1.硬件原理 1.蜂鸣器正极接单片机20号引脚VCC,负极接19号引脚P1.7 2.20MH…...

Web3.0时代:区块链DAPP将如何颠覆传统模式
小编介绍:10年专注商业模式设计及软件开发,擅长企业生态商业模式,商业零售会员增长裂变模式策划、商业闭环模式设计及方案落地;扶持10余个电商平台做到营收过千万,数百个平台达到百万会员,欢迎咨询。 随着…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...
