当前位置： 首页 > news >正文

【追求卓越08】算法--排序算法

news 2025/8/22 15:41:22

引导

今天开始介绍我们在工作中经常遇到的算法--排序。排序算法有很多，我们主要介绍以下几种：

  • 冒泡排序
  • 插入排序
  • 选择排序
  • 归并排序
  • 快速排序
  • 计数排序
  • 基数排序
  • 桶排序

我们需要了解每一种算法的定义以及实现方式，并且掌握如何评价一个排序算法。今天我们来学习冒泡排序，插入排序，选择排序。

如何评价排序算法

评价算法的优劣主要从以下几个方面考虑：

  1. 最好情况，最坏情况，平均情况时间复杂度
  2. 时间复杂度的系数，低阶，常系数都需要考虑进去
  3. 是否是原地排序？
  4. 算法是否稳定？

第一点毋庸置疑，是我们主要的依判方式；

第二点,我们常常在计算复杂度时会忽略低阶和常系数。这是因为当数据量很大，n趋向于无穷时。但是在实际工作中，我们的数据量不会这么大。所以这些低阶和常数就需要考虑进去了。

第三点：原地排序就是对空间复杂度的一种描述，当排序算法的空间复杂度为O(1)时，我们就称为原地排序

第四点：算法的稳定指的时排序之后是否会将值相同的数据对象改变位置。比如
1，3（1），5，7，9，3（2）,这组数据进行排序之后，3(2)还会在3(1)之后吗？

        算法的稳定性主要是用于对一组数据进行多次排序时进行参考。比如你要将一组数据按照时间和值大小按照时间从先到后，值从小到大进行排序。一般是按照时间排序，在对值进行排序。但是如果在进行值排序时，使用的是不稳定的算法，那么就会出现问题。（值相等，但时间可能有错误）

冒泡排序

冒泡排序原理：

  1. 比较相邻的元素。如果第一个比第二个大，就交换他们两个。
  2. 对每一对相邻元素做同样的工作，从开始第一对到结尾的最后一对。在这一点，最后的元素应该会是最大的数。
  3. 针对所有的元素重复以上的步骤，除了最后一个。
  4. 持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

int bubblesort(int a[],int len)
{
    int i,j=0;
    int temp = 0;
    for(i = 0; i < len ; i++)
    {
        for(j = 0 ; j < len - i - 1  ; j++)
        {
            if(a[j] > a[j+1])
            {
                 temp = a[j];
                 a[j] = a[j+1];
                 a[j+1] = temp;
            }
        }
    }
    return 0;
}

以上是一般的冒泡排序代码，但是可以稍微优化一下：

int bubblesort(int a[],int len)
{
    int i,j=0;
    int temp = 0;
    int flag = 0;
    for(i = 0; i < len ; i++)
    {
        flag = 0;
        for(j = 0 ; j < len - i - 1  ; j++)
        {
            if(a[j] > a[j+1])
            {
                 flag = 1;
                 temp = a[j];
                 a[j] = a[j+1];
                 a[j+1] = temp;
            }
        }
        if(flag == 1)
            break;
    }
    return 0;
}

        该优化过的代码，加了一个判断标志，当某一次冒泡没有进行数据交互，说明剩下的都是排好序了。故可以直接退出。

分析：

时间复杂度：通过代码实现我们可以知道，冒泡排序的复杂度为O((1+n)*n/2)。

空间复杂度：由于只有一个temp的额外变量，故空间复杂度为O(1),为原地排序。

稳定性:我们在判断时，只要确保a[j]>a[j+1]为判断条件即可保证稳定性。

总结：冒泡排序是原地排序，并且稳定，复杂度为O((1+n)*n/2)的算法。

插入排序

        插入排序原理比较难描述，类似于我们斗地主理牌的过程，原先是乱序的，左边第一个作为依据，依次在乱序中找第一个放到有序中。

int insertsort(int a[],int len)
{
    // 插入排序，a表示数组，n表示数组大小
    if (len <= 1) return;
    int i = 0;
    for (i = 1; i < len; ++i) {
        int value = a[i];
        int j = i - 1;
        // 查找插入的位置
        for (; j >= 0; --j) {
            if (a[j] > value) {
                a[j+1] = a[j];  // 数据移动
            } else {
                break;
            }
        }
        a[j+1] = value; // 插入数据
    }
}

分析：

复杂度：通过代码可知，插入排序的复杂度比较难以计算，但可以确定的是O(n^2)。

空间复杂度：O(1),故是原地排序

稳定性：判断条件是a[j] > value，即可保证稳定性

总结：插入排序是原地排序，具有稳定性的算法。

选择排序

选择排序原理：

  1. 设置最值位置标记，逐轮扫描未排序部分元素最值。
  2. 每一轮扫描过程中，以未排序部分首部元素为基准(将位置标记设置为未排序首元素下标)与后续元素进行比较。
  3. 遇到更小(或更大)的元素则将位置标记修改为其下标，直至扫描完成，将标记位置的元素与未排序部分首元素交换位置。
  4. 至多进行n-1轮扫描，序列完全有序。

其实，我认为选择排序和插入排序类似，它比较的操作是在无序中，在无序中找到最值。插入排序是在有序中比较，将新值放到合适的地方。

int selectsort(int a[],int len)
{
    if (len <= 1)
        return 0;
    int i = 0;
    int j = 0;
    int index = 0;
    int temp = 0;
    for(i = 0 ; i < len ;i ++)
    {
        for(j = i ,index = i; j < len; j ++ )
        {
            if(a[index] > a[j])
                index = j;
        }
        temp = a[i];
        a[i] = a[index];
        a[index] = temp;
    }
    return 0;
}

分析：
空间复杂度：为O(1),原地排序
时间复杂度：为O(n^2)。
稳定性：不稳定。因为找到最小值之后，需要于无序中的首元素交换，这里会出现不稳定现象。例如：

比如 5，8，5，2，9 这样一组数据，使用选择排序算法来排序的话，第一次找到最小元素 2，与第一个 5 交换位置，那第一个 5 和中间的 5 顺序就变了，所以就不稳定了。

总结：选择排序是原地排序，复杂度为O(n^2),不稳定的算法

归并排序

归并操作的工作原理如下：

如果要排序一个数组，我们先把数组从中间分成前后两部分，然后对前后两部分分别排序，再将排好序的两部分合并在一起，这样整个数组就都有序了。

其中的问题就是如何获取两个排好序的部分：当数组长度变为1，是不是就已经相当于排好序了（实际上不需要再排序），这个时候再将长度为1的数组合并到一起，就变成了长度为2的有序数组。

int merge(int a[],int left , int mid, int right)
{
    int * arr = (int
*)malloc(sizeof(int)*
(right-left+1));
    memset(arr,0,sizeof(int)*(right-left+1));
    int i = left;
    int j = mid+1;
    int m = 0;
    while(i <= mid && j <= right)
    {
        if(a[i]< a[j])
        {
            arr[m++] = a[i++];
        }
        else
        {
            arr[m++] = a[j++];
        }
    }
    if(i>mid)
    {
        for(;  j <= right ; j++)
            arr[m++] = a[j];
    }
    else
    {
        for(; i <= mid ; i++)
            arr[m++] = a[i];
    }
    for(i = 0 ; i <= right - left; i++)
        a[left+i] = arr[i];
    return 0;
}
int mergesort_separate(int a[], int start, int end)
{
    if(start >= end)
        return 0;
    int i =(int) ((start+end)/2);
    mergesort_separate(a,start,i);
    mergesort_separate(a,i+1,end);
    merge(a,start,i,end);
}
int mergesort(int a[],int len)
{
    mergesort_separate(a,0,len-1);
}

其中merge()函数是核心。需要好好品味。

分析：

从归并算法的实现中，我们依旧从稳定性，是否是原地排序？，时间复杂度来分析。

稳定性：我们知道merge()函数包括主要的数据搬移工作，只要保证这里稳定即可。是可以满足的。所以归并排序是稳定算法。

原地排序：在merge()函数中，我们需要将两个有序数组合并，需要用到额外的临时数组，故空间复杂度是O(n),故归并排序不是原地排序

时间复杂度：我们知道归并排序的时间复杂度是O(nlogn)，但是至于怎么推导出来的，肯定很多人都处于茫然状态。这里我就稍微推导一下，看不懂没有关系。

假设数据量为n，归并排序的复杂度为T(n),由于归并排序的思路是将大问题分解为小问题，
再将小问题的结果合并。
故T(n) = T(n/2)+T(n/2)+n;其中n表示将结果合并消耗的时间。
T(n) = 2
*T(n/2)+n = 4*
T(n/4)+4n = 8
T(n/8)+8n
*T(n) = 2^kT(n/2^k)+2^k*
n
当 n/2^k=1时，T(n) = 2^k+2^k*n，将k带入得：T(n) = logn+n*logn=n*logn。

故归并排序的时间复杂度为O(n*logn);

快速排序

快速排序原理：

如果要排序数组中下标从 p 到 r 之间的一组数据，我们选择 p 到 r 之间的任意一个数据作为 pivot（分区点）。我们遍历 p 到 r 之间的数据，将小于 pivot 的放到左边，将大于 pivot 的放到右边，将 pivot 放到中间。

经过这一步骤之后，数组 p 到 r 之间的数据就被分成了三个部分，前面 p 到 q-1 之间都是小于 pivot 的，中间是 pivot，后面的 q+1 到 r 之间是大于 pivot 的

int sort(int a[],int start, int end)
{
    int target = a[end];
    int i = start;
    int j = start;
    int temp = 0;
    for(j = start ; j < end ; j++)
    {
        if(a[j] < target)
        {
            temp = a[i];
            a[i] = a[j];
            a[j] = temp;
            i++;
        }
    }
    temp = a[i];
    a[i]=target;
    a[end] = temp;
    return i;
}
int quicksort(int a[], int start, int end)
{
    if(start >= end)
        return 0;
    int mid = sort(a,start,end);
    quicksort(a,start,mid-1);
    quicksort(a,mid+1,end);
}

分析

稳定性：在快速排序中，需要对数组进行搬移，比如：6，8，7，6,3，5，4,会发生不稳定。所以快速排序是不稳定。

原地排序：由于交换数据时，只需要一个临时变量，空间复杂度为O(1),故快速排序是原地排序。

时间复杂度：同归并排序同理，快速排序的事件复杂度也是O(n*logn)。

注意：快速排序 在大部分情况下的时间复杂度都可以做到 O(nlogn)，只有在极端情况下，才会退化到 O(n^2)。

问题：O(n) 时间复杂度内求无序数组中的第 K 大元素？

思路：一般情况下，我们需要先进行排序，再通过下标直接访问。虽然数组的访问复杂度是O(1),但是排序较为耗时，即使使用归并排序和快速排序也是O(n*logn)。

       既然该题出现在这里，很容易想到会用到归并排序和快速排序。比较一下两者实现的原理，发现快速排序比较适合这道题。当我们sort()返回的mid等于K-1。是不是就表示a[mid],就是第K大的元素（mid左边由K-1个数，都比mid小。虽然不是有序，但没有影响）。当mid+1<K时，说明第K大的元素在[mid+1,end]之间。反之在[start,mid-1]之间。


int sort(int a[],int start, int end)
{
    int target = a[end];
    int i = start;
    int j = start;
    int temp = 0;
    for(j = start ; j < end ; j++)
    {
        if(a[j] < target)
        {
            temp = a[i];
            a[i] = a[j];
            a[j] = temp;
            i++;
        }
    }
    temp = a[i];
    a[i]=target;
    a[end] = temp;
    return i;
}
int findKnum(int a[], int start ,int end,int K)
{
    int mid = sort(a,start,end);
    int result = 0;
    if(mid+1 == K )
    {
        result=  a[mid];
    }
    else if(mid+1 < K)
    {
      result = findKnum(a,mid+1,end,K);
    }
    else
    {
      result = findKnum(a,start,mid-1,K);
    }
   return result;
}
int main()
{
        int a[10]={1,3,5,7,4,9,10,8,6,2};
        printf("%d\n",findKnum(a,0,9,6));
        return 0;
}

分析：为什么该解法的复杂度是O(n)呢？

假设复杂度为T(n),我们已知sort的复杂度是O(n),当我们第一次没有找到正确元素是，我们只需在n/2个数据中进行查找。同理接下来的复杂度是n/4,n/8...直至数组长度为1，及找到对应数据（最坏情况）。这很明显是等比数列。T(n)=2n-1=O(n)。

桶排序

桶排序原理：核心思想是将要排序的数据分到几个有序的桶里，每个桶里的数据再单独进行排序。桶内排完序之后，再把每个桶里的数据按照顺序依次取出，组成的序列就是有序的了。

复杂度为什么是O(n)?

如果要排序的数据有 n 个，我们把它们均匀地划分到 m 个桶内，每个桶里就有 k=n/m 个元素。每个桶内部使用快速排序，时间复杂度为 O(k * logk)。m 个桶排序的时间复杂度就是 O(m * k * logk)，因为 k=n/m，所以整个桶排序的时间复杂度就是 O(n*log(n/m))。当桶的个数 m 接近数据个数 n 时，log(n/m) 就是一个非常小的常量，这个时候桶排序的时间复杂度接近 O(n)。

注意：

  1. 上述的情况是桶排序最好的情况，即每个桶中的数据均匀。最坏情况，所有数据都集中再一个桶中的话，那么复杂度就会退化到O(nlogn)
  2. 我觉得桶排序的思想并不困难，关键在于元素值域的划分，也就是值到桶之间的映射规则。(确定规则之后，就可以确定桶的数量f(max) - f(min)+1)。
  3. 实际上桶排序是用空间换时间来提高处理速度的。

#include<stdlib.h>
#include<stdio.h>
#include<string.h>
int sort(int a[],int start, int end)
{
    int target = a[end];
    int i = start;
    int j = start;
    int temp = 0;
    for(j = start ; j < end ; j++)
    {
        if(a[j] < target)
        {
            temp = a[i];
            a[i] = a[j];
            a[j] = temp;
            i++;
        }
    }
    temp = a[i];
    a[i]=target;
    a[end] = temp;
    return i;
}
int quicksort(int a[], int start, int end)
{
    if(start >= end)
        return 0;
    int mid = sort(a,start,end);
    quicksort(a,start,mid-1);
    quicksort(a,mid+1,end);
}
int insertnum(int a[],int len,int num)
{
    int i = 0;
    while(i<len)
    {
        if(a[i]==0)
        {
            a[i] = num;
            break;
        }
        i++;
    }
    return 0;
}
int main()
{
        int a[20]={1,3,5,7,4,9,10,8,6,2,12,13,15,14,17,16,19,18,20,11};
        //这个二位数组是我们根据数据源分析出来的
        int buket[5][5] = {0};
        int i = 0;
        for(i = 0 ; i < 20 ; i++)
        {
            insertnum(buket[a[i]/5],5,a[i]);
        }
        for(i = 0 ; i < 5 ;i ++)
            quicksort(buket[i],0,4);

        int j = 0;
        for(i = 0 ; i < 5 ; i ++)
        {
            for(j = 0 ; j < 5 ; j ++)
                buket[i][j] == 0 ? :printf("%d\n",buket[i][j]);

        }
        return 0;
}

分析

        由于数据源较为简单和均匀，所以我选择间隔为5作为映射函数。将数据放到[0,4]5个桶中，再将每个桶中的数据进行排序，再一次将五个桶中的数据依次输出。

        桶排序只要映射函数合理，那么其复杂度是O(n),这一点我们已经介绍过了。

        桶排序需要额外的内存用于桶，空间复杂度是O(n+m),其中m是桶的个数。

        桶排序在将数据隐射到桶的过程是稳定的。但是在排序的过程中如果你选择的是快速排序，就不是稳定的了，如上面的例子。若选择归并排序，就是稳定排序。

计数排序

计数排序和桶排序的原理类似，更像是特例：

        当要排序的 n 个数据，所处的范围并不大的时候，比如最大值是 k，我们就可以把数据划分成k个桶。每个桶内的数据值都是相同的，省掉了桶内排序的时间。

int findmaxmin(int a[],int len, int*max ,int *min)
{
    if(len == 0)
        return 0;
    int i = 0;
    *max = a[0];
    *min = a[0];
    for(i = 0; i < len ; i++)
    {
        if(a[i] > *max)
            *max = a[i];
        else if(a[i] < *min)
            *min = a[i];
    }
    return 0;
}
int countsort(int a[],int len)
{
    int max,min = 0;
    findmaxmin(a,len,&max,&min);
    int *count = (int *) malloc((max-min+1)*sizeof(int));
    memset(count,0,(max-min+1)*sizeof(int));
    int i = 0 ;
    for(i = 0 ; i < len ; i++)
         count[a[i]-min]++; /
*count*
/
    for(i = 1 ; i < max-min+1 ; i++)
        count[i] += count[i-1];
    int
*target = (int *
**) malloc(len**
sizeof(int));
*    memset(target,0,len*
sizeof(int));
    for(i = 0 ; i < len ; i++)
    {
        target[--count[a[i] - min]] = a[i];
    }
    memcpy(a,target,sizeof(int)*len);
    free(count);
    free(target);
}
int main()
{
        int a[20]={10,12,11,13,13,15,14,12,11,14,15,15,14,13,12,11,13,12,10,10};
        countsort(a,20);
        int i = 0;
        for(i = 0 ; i < 20 ; i ++)
        {
            printf("%d\n",a[i]);
        }
        return 0;
}

分析

        计数排序的时间复杂度为O(n),在算法的过程中涉及到了4个循环.第一个是在数据源中找到最大最小值；第二次循环是遍历数据源，统计数据出现的次数；第三次遍历确认数据的位置；第四次遍历，是进行排序。

计数排序的空间复杂度是O(n+max-min)。故不是原地排序。

        计数排序在进行排序时在第四个循环中进行的。若判断条件为for(i = len -1 ; i > 0 ; i-- )，排序就是稳定的。否则就不是稳定的。

        注意：计数排序只能用在数据范围不大的场景中，如果数据范围 k 比要排序的数据 n 大很多，就不适合用计数排序了。而且，计数排序只能给非负整数排序，如果要排序的数据是其他类型的，要将其在不改变相对大小的情况下，转化为非负整数。

基数排序

基数排序原理：其原理是将整数按位数切割成不同的数字，然后按每个位数分别比较。

        我觉得基数排序和计数排序类似，不过计数排序要求数据范围max和min的差距不要太大。但是当数据范围很大时，很明显计数排序和桶排序就不能在使用了。而基数排序就是从位的角度切入到计数排序。

#include<stdlib.h>
#include<stdio.h>
#include<string.h>
int findmaxbit(int a[],int len)
{
    if(len == 0)
        return 0;
    int bit = 0;
    int temp= bit;
    int i = 0 ;
    int num = 0;
    for(i = 0 ; i < len ; i++)
    {
        num = a[i];
        temp = 0;
        while(num != 0 )
        {
            num/=10;
            temp++;
        }
        if(temp > bit)
           bit = temp;
    }
    return bit;
}
int basesort(int a[],int len)
{
    int max,min = 0;
    int bit = findmaxbit(a,len);

    int
*temp = (int*
)malloc(sizeof(int)*len);
    int count[10] = {0};
    int i = 0;
    int j = 0;
    int radix = 1;
    for(j = 0 ; j < bit ; j++)
    {
        memset(count,0,sizeof(int)*10);
        memset(temp,0,sizeof(int)*len);
        for(i = 0 ; i < len ; i++)
            count[((int) a[i]/radix) %10]++;
        for(i = 1 ; i < 10 ; i++)
             count[i]+= count[i-1];
        for(i = len -1  ; i >= 0  ; i--)
            temp[--count[((int) a[i]/radix) %10]]=a[i];
        memcpy(a,temp,sizeof(int)
len);
*        radix*
=10;
    }
    free(temp);
    return 0;
}
int main()
{
        int a[10]={56,123,12315,5312366,1234783,245671,123421,568421,643261,93458};
         basesort(a,10);

        int i = 0;
        for(i = 0 ; i < 10 ; i ++)
        {
            printf("%d\n",a[i]);
        }
        return 0;
}

分析

基数排序的时间复杂度是O(n)。

基数排序的空间复杂度是O(n),相对于前两者，减少了一些，所以不是原地排序。

基数排序涉及到数据的搬移和计数排序相似，故基数排序也是稳定排序。

        注意：基数排序对要排序的数据是有要求的，需要可以分割出独立的“位”来比较，而且位之间有递进的关系，如果 a 数据的高位比 b 数据大，那剩下的低位就不用比较了。除此之外，每一位的数据范围不能太大，要可以用线性排序算法来排序，否则，基数排序的时间复杂度就无法做到 O(n) 了。

总结

        本章我们接触了冒泡排序，插入排序，选择排序，了解了其定义和代码实现

        也介绍了如何评价排序算法的依据。其中冒泡排序和插入排序是稳定的，选择排序是不稳定的。

冒泡排序和插入排序相比较而言，其中的交换数据操作较多：

冒泡：

C
if(a[j] > a[j+1])
{
     flag = 1;
     temp = a[j];
     a[j] = a[j+1];
     a[j+1] = temp;
}

插入：

C
if (a[j] > value)
{
    a[j+1] = a[j];  // 数据移动
} else
{
    break;
}

故综上所述，这三个算法的优先级：插入排序>冒泡排序>选择排序。

        归并排序和快速排序，两者的时间复杂度都是O(n*logn)。但是由于归并排序并不是原地排序，所以消耗内存较多。而快速排序是原地排序，解决了归并排序消耗内存较多的问题。快速排序是不稳定的算法，归并排序是稳定算法。

        归并排序在任何情况下，时间复杂度都是O(nlogn);快速排序虽然在最坏情况下的时间复杂度为O(n^2),但大部分情况下的复杂度都是O(nlogn)。

        桶排序，计数排序，基数排序。它们的空间复杂度都是O(n),因为它们不涉及到比较操作（每个元素之间比较），并且利用了额外的空间，得到了很高的效率。虽然这三种排序拥有很高的效率，但是它们的适用情景较少，对数据要求较为严苛。

桶排序：要求数据均匀分布，或者能够给予一个优秀的映射函数。

计数排序：要求数据源中最大值和最小值的范围较小。

基数排序：要求数据源是正正数，并且范围不能太大。

相关文章：

【追求卓越08】算法--排序算法

引导 今天开始介绍我们在工作中经常遇到的算法--排序。排序算法有很多&#xff0c;我们主要介绍以下几种&#xff1a; 冒泡排序 插入排序 选择排序 归并排序 快速排序 计数排序 基数排序 桶排序 我们需要了解每一种算法的定义以及实现方式&#xff0c;并且掌握如何评…...

编程日记 2023/11/28 6:42:53

Linux fork笔试练习题

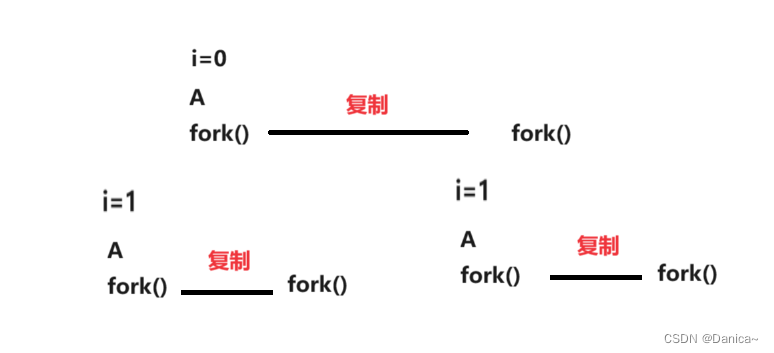
1.打印结果&#xff1f; #include <stdio.h> #include <unistd.h> #include <stdlib.h>int main() {int i0;for(;i<2;i){fork();printf("A\n");}exit(0); } 结果打印 A A A A A A 2.将上面的打印的\n去掉,结果如何? printf("…...

编程日记 2023/11/28 6:41:52

Jenkins 整合 Docker 自动化部署

Docker 安装 Jenkins 配置自动化部署 1. Docker 安装 Jenkins 1.1 拉取镜像文件 docker pull jenkins/jenkins1.2 创建挂载文件目录 mkdir -p $HOME/jenkins_home1.3 启动容器 docker run -d -p 8080:8080 -v $HOME/jenkins_home:/var/jenkins_home --name jenkins jenkin…...

编程日记 2023/11/28 6:40:51

竞赛选题 题目：基于大数据的用户画像分析系统 数据分析 开题

文章目录 1 前言2 用户画像分析概述2.1 用户画像构建的相关技术2.2 标签体系2.3 标签优先级 3 实站 - 百货商场用户画像描述与价值分析3.1 数据格式3.2 数据预处理3.3 会员年龄构成3.4 订单占比 消费画像3.5 季度偏好画像3.6 会员用户画像与特征3.6.1 构建会员用户业务特征标签…...

编程日记 2023/11/28 6:39:49

selenium已知一个元素定位同级别的另一个元素

1.需求与实际情况 看下图来举例 &#xff08;1&#xff09;需求 想点击test22&#xff08;即序号-第9行&#xff09;这一行中右边的“复制”这一按钮 &#xff08;2&#xff09;实际情况 只能通过id或者class定位到文件名这一列的元素&#xff0c;而操作这一列的元素是不…...

编程日记 2023/11/28 6:38:48

Kotlin中 for in 是有序的吗？forEach呢？

我们要遍历一个数组、一个列表&#xff0c;经常会用到kotlin的 for in 语法&#xff0c;但是 for in 是不是有序的呢&#xff1f;forEach是不是有序的呢&#xff1f;这就需要看一下它们的本质了。 数组的 for in // 调用&#xff1a; val arr arrayOf(1, 2, 3) for (ele in …...

编程日记 2023/11/28 6:36:45

每日一练2023.11.27———连续因子【PTA】

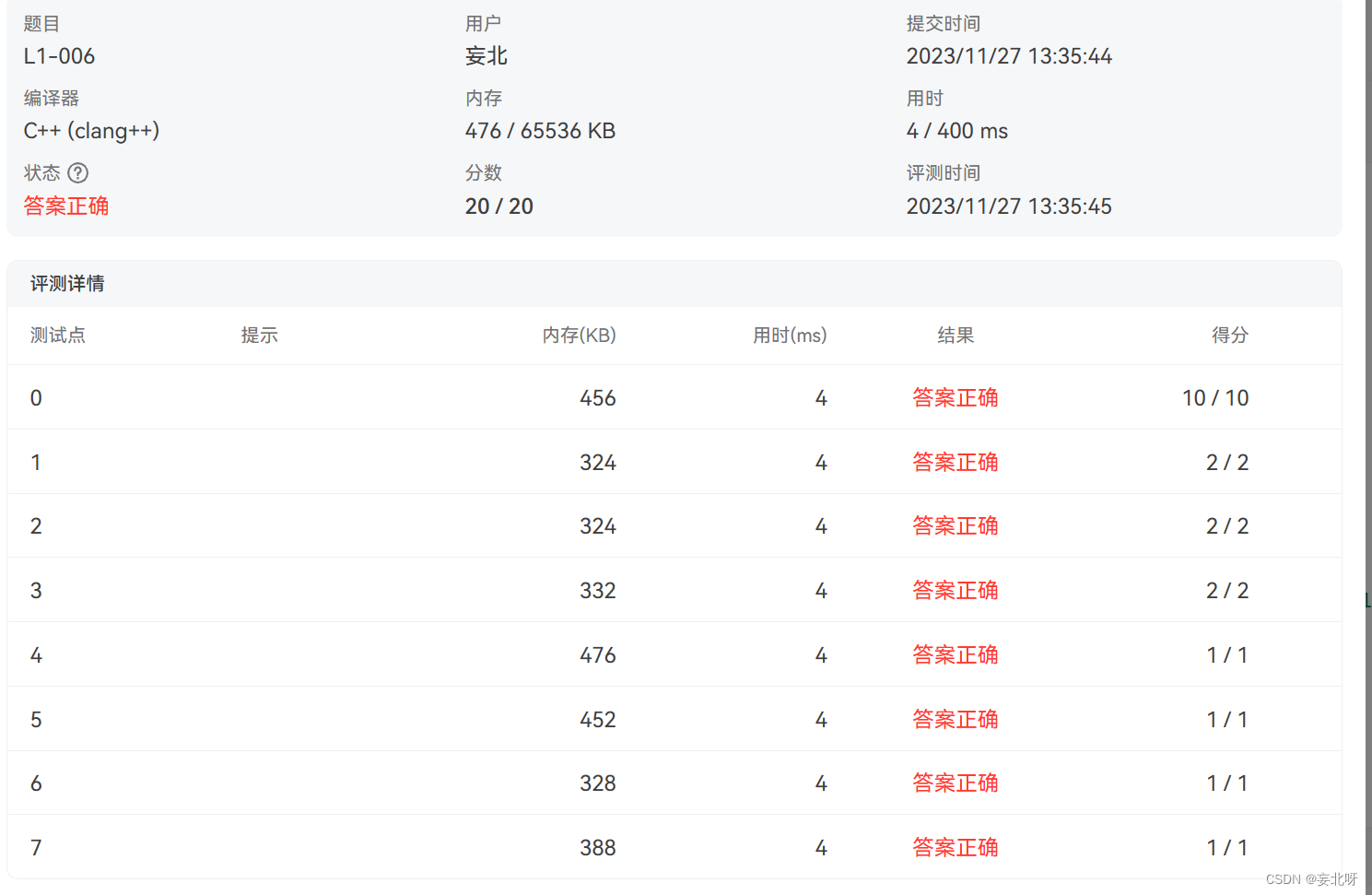
题目链接&#xff1a;L1-006 连续因子​​​​​​​ 题目要求&#xff1a; 一个正整数 N 的因子中可能存在若干连续的数字。例如 630 可以分解为 3567&#xff0c;其中 5、6、7 就是 3 个连续的数字。给定任一正整数 N&#xff0c;要求编写程序求出最长连续因子的个数&#…...

编程日记 2023/11/28 6:35:43

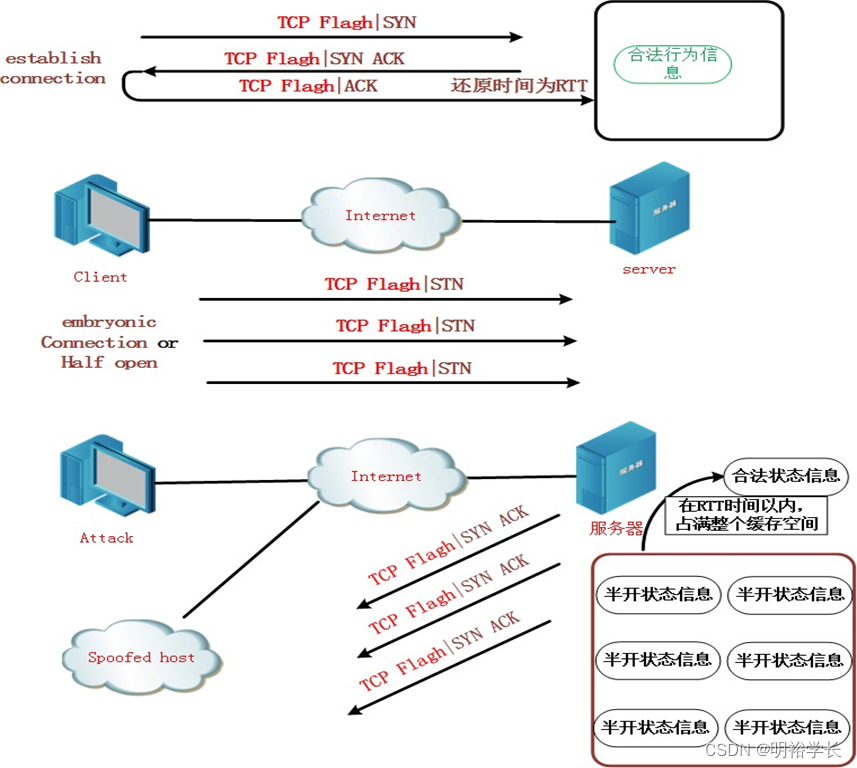
P8A002-CIA安全模型-配置Linux描述网络安全CIA模型之可用性案例

【预备知识】 可用性（Availability） 数据可用性是一种以使用者为中心的设计概念，易用性设计的重点在于让产品的设计能够符合使用者的习惯与需求。以互联网网站的设计为例，希望让使用者在浏览的过程中不会产生压力或感到挫折，并能让使用者在使用网站功能时，能用最少的努力…...

编程日记 2023/11/28 6:34:42

SpringCloudAlibaba之sentinel 流量卫兵(流控，熔断降级) ——详细讲解

目录 一、什么是sentinel 二、sentinel使用 1. sentinel dashboard的安装 2.启动 3.访问web界面 ​编辑 4.登录 三、sentinel 实时监控服务 1.创建项目引入依赖 2.配置 3.启动服务 4.访问dashboard界面查看服务监控 5.开发服务 6.启动进行调用 7.查看监控界面 四、senti…...

编程日记 2023/11/28 6:33:40

C++封装dll和lib 供C++调用

头文件interface.h #pragma once #ifndef INTERFACE_H #define INTERFACE_H #define _CRT_SECURE_NO_WARNINGS #define FENGZHUANG_API _declspec(dllexport) #include <string> namespace FengZhuang {class FENGZHUANG_API IInterface {public:static IInterface* Cre…...

编程日记 2023/11/28 6:32:38

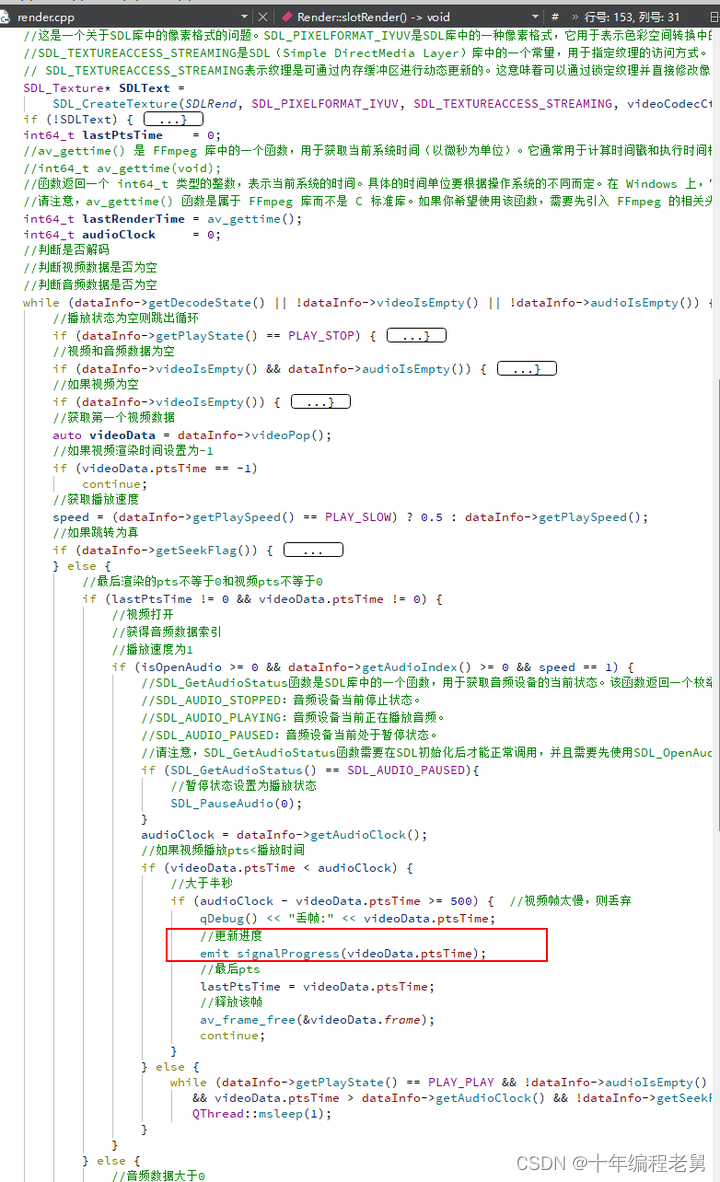
ffmpeg播放器实战（播放器流程）

1.流程图 1.main窗口创建程序窗口 程序窗口构造函数执行下面内容 2.开启播放 3.开启解码 4.开启渲染 5.反馈给ui 本文福利&#xff0c; 免费领取C音视频学习资料包学习路线大纲、技术视频/代码&#xff0c;内容包括&#xff08;音视频开发&#xff0c;面试题&#xff0c;FFmpeg…...

编程日记 2023/11/28 6:30:36

Android 13.0 开机过滤部分通知声音(莫名其妙的通知声音)

1.概述 在13.0的系统定制开发产品的中，有时候在系统开机的时候会有一些通知的声音，但是由于系统模块太多，也搞不清楚到底是哪个模块发出的通知声音，所以就需要从通知的流程来屏蔽这些通知声音,接下来看具体怎么实现在开机的时候过滤开机声音的功能 2.开机过滤部分通知声音…...

编程日记 2023/11/28 6:28:33

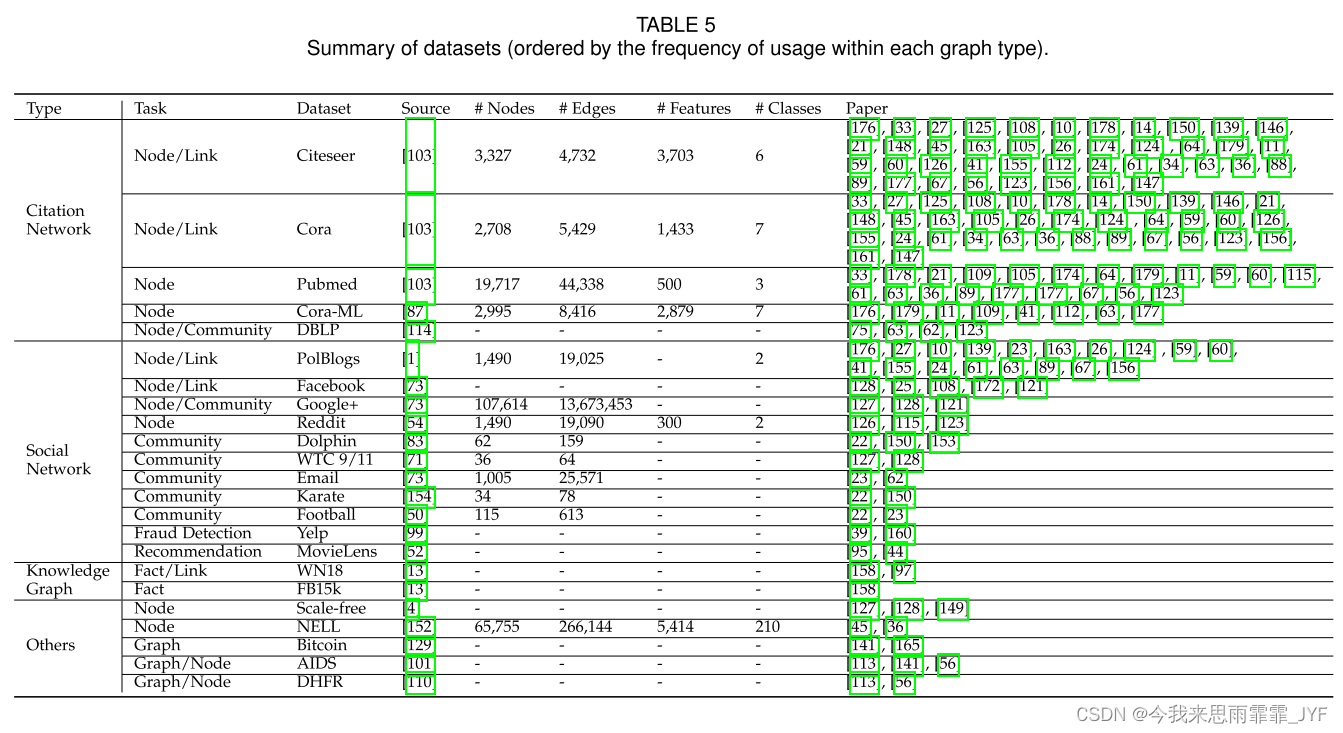
Adversarial Attack and Defense on Graph Data: A Survey（2022 IEEE Trans）

Adversarial Attack and Defense on Graph Data: A Survey----《图数据的对抗性攻击和防御&#xff1a;综述》 图对抗攻击论文数据库&#xff1a; https://github.com/safe-graph/graph-adversarial-learning-literature 摘要 深度神经网络&#xff08;DNN&#xff09;已广泛应…...

编程日记 2023/11/28 6:25:29

css中flex两列布局（一列自适应其他固定）

问题 最近写一个布局的时候&#xff0c;遇到一个问题。如下图的布局。在没有图片的时候布局是正常的&#xff0c;如果有图片且设置了width:100%;height: 100%; 则会出现图片将自适应布局撑开的情况。 我的解决方式是让图片不缩放&#xff0c;图片外层再添加一个div元素。形如…...

编程日记 2023/11/28 6:24:28

【深度学习】gan网络原理实现猫狗分类

【深度学习】gan网络原理实现猫狗分类 GAN的基本思想源自博弈论你的二人零和博弈&#xff0c;由一个生成器和一个判别器构成&#xff0c;通过对抗学习的方式训练&#xff0c;目的是估测数据样本的潜在分布并生成新的数据样本。 1.下载数据并对数据进行规范 transform tran…...

编程日记 2023/11/28 6:23:26

⑨【Stream】Redis流是什么？怎么用？： Stream [使用手册]

个人简介&#xff1a;Java领域新星创作者&#xff1b;阿里云技术博主、星级博主、专家博主&#xff1b;正在Java学习的路上摸爬滚打&#xff0c;记录学习的过程~ 个人主页&#xff1a;.29.的博客 学习社区&#xff1a;进去逛一逛~ ⑨Redis Stream基本操作命令汇总 一、Redis流 …...

编程日记 2023/11/28 6:22:25

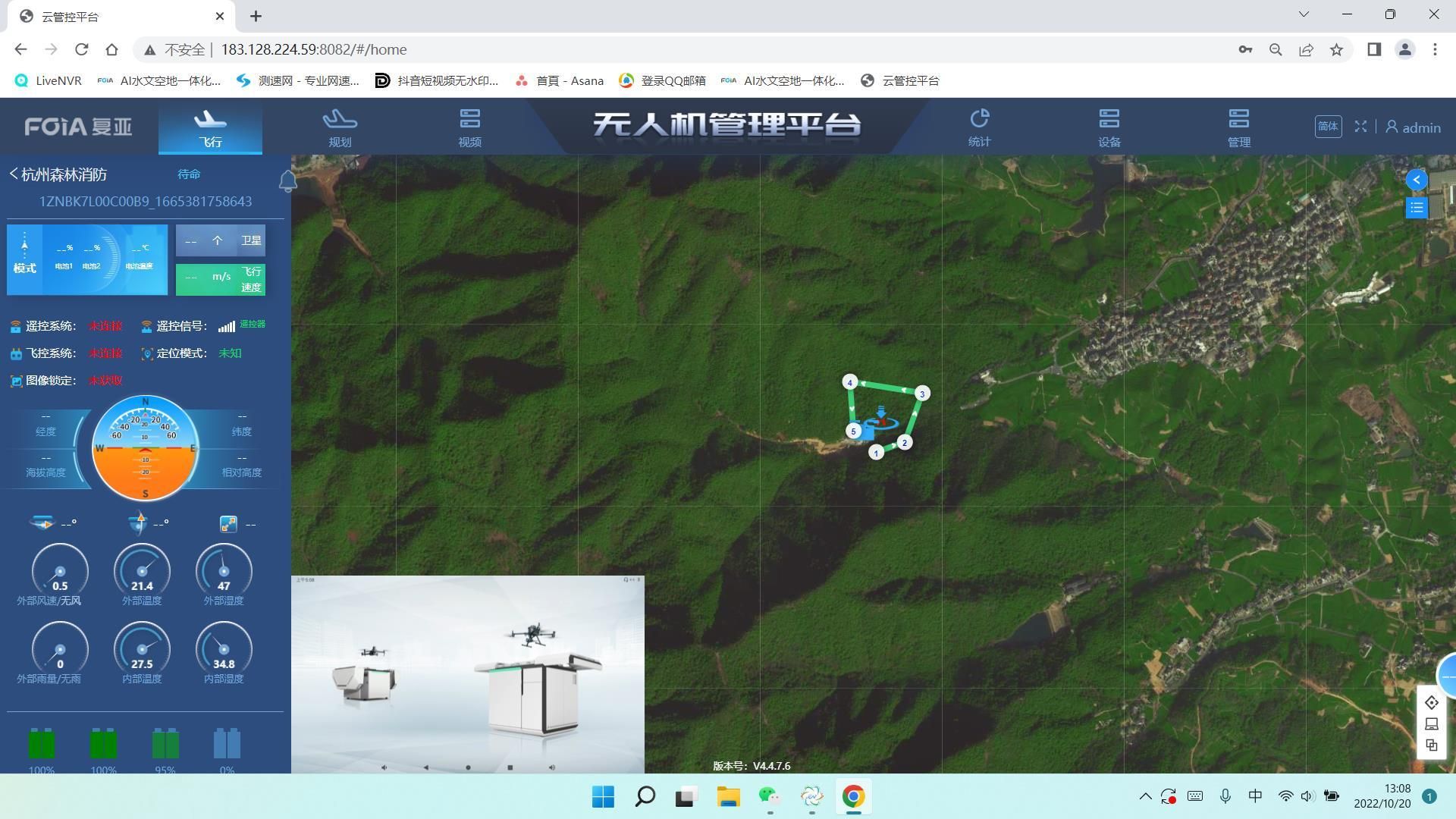
浙江启用无人机巡山护林模式，火灾扑救效率高

为了保护天然的森林资源&#xff0c;浙江当地林业部门引入了一种创新技术&#xff1a;林业无人机。这些天空中的守护者正在重新定义森林防火和护林工作的方式。 当下正值天气干燥的季节&#xff0c;这些无人机开始了它们的首次大规模任务。它们在指定的林区内自主巡逻&#xff…...

编程日记 2023/11/28 6:21:23

Starrocks异步物化视图的使用以及注意事项

最近在使用starrocks来进行实时数据项目的开发&#xff0c;尝试使用了一下starrocks的异步物化视图。 使用版本: 3.1.2-4f3a2ee 创建三个测试表, 注意只有test_mv_table1为分区表&#xff0c;其他两个都是非分区表: CREATE TABLE test_mv_table1 (periodday DATE NOT NULL CO…...

编程日记 2023/11/28 6:20:22

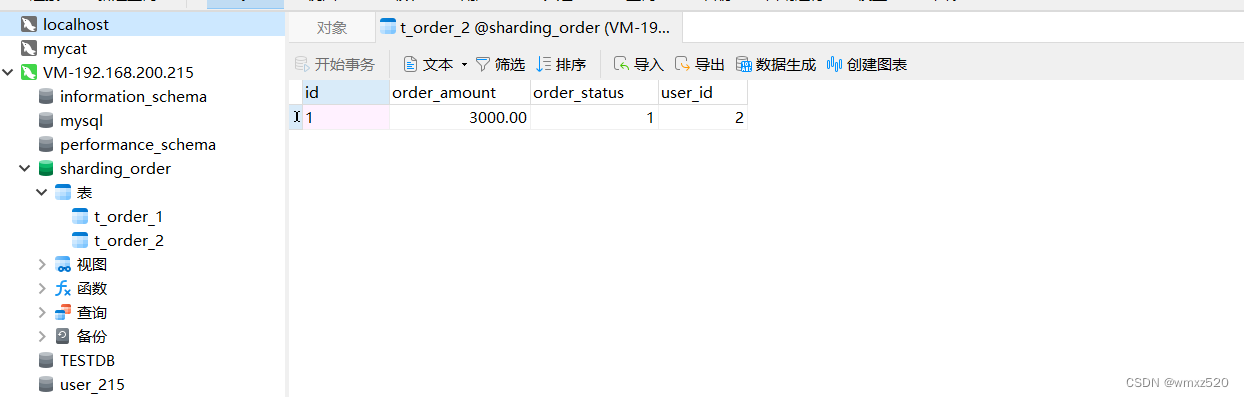
SpringBoot整合Sharding-Jdbc实现分库分表和分布式全局id

SpringBoot整合Sharding-Jdbc Sharding-Jdbc sharding-jdbc是客户端代理的数据库中间件&#xff1b;它和MyCat最大的不同是sharding-jdbc支持库内分表。 整合 数据库环境 在两台不同的主机上分别都创建了sharding_order数据库&#xff0c;库中都有t_order_1和t_order_2两张…...

编程日记 2023/11/28 6:19:20

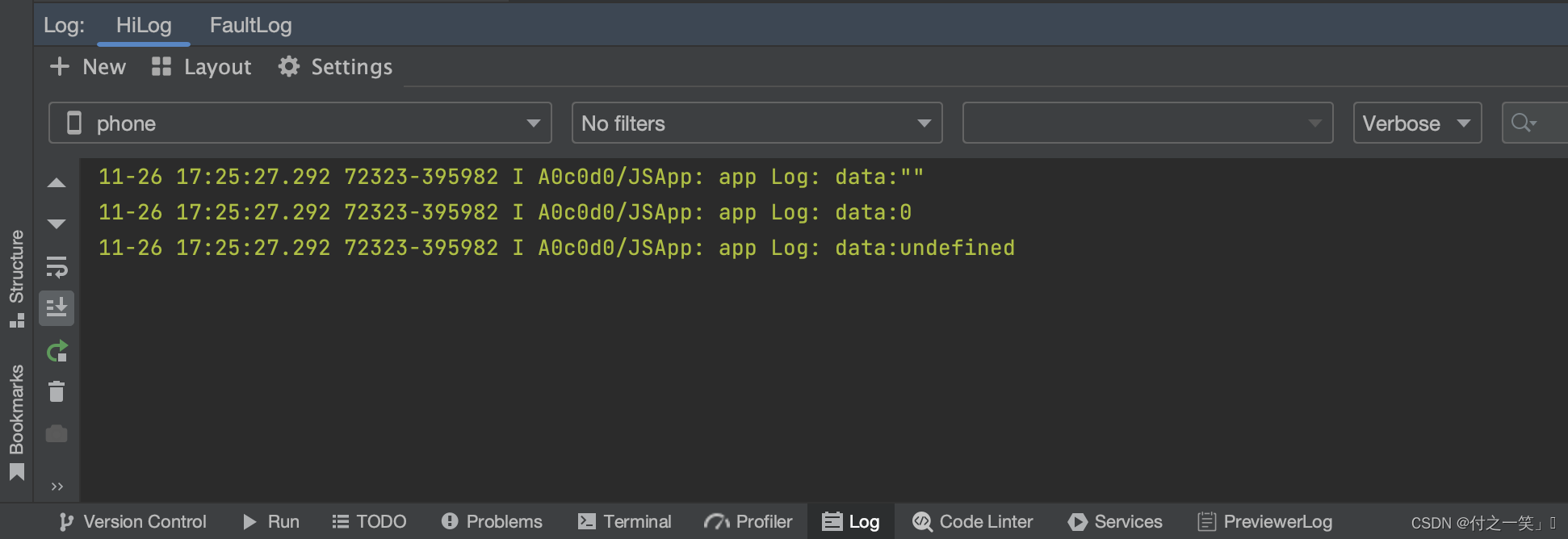
「江鸟中原」有关HarmonyOS-ArkTS的Http通信请求

一、Http简介 HTTP&#xff08;Hypertext Transfer Protocol&#xff09;是一种用于在Web应用程序之间进行通信的协议&#xff0c;通过运输层的TCP协议建立连接、传输数据。Http通信数据以报文的形式进行传输。Http的一次事务包括一个请求和一个响应。 Http通信是基于客户端-服…...

编程日记 2023/11/28 6:18:19

以下是对华为 HarmonyOS NETX 5属性动画（ArkTS）文档的结构化整理，通过层级标题、表格和代码块提升可读性：

一、属性动画概述NETX 作用&#xff1a;实现组件通用属性的渐变过渡效果&#xff0c;提升用户体验。支持属性&#xff1a;width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项&#xff1a; 布局类属性&#xff08;如宽高&#xff09;变化时&#…...

编程新知 2025/8/22 3:26:18

.Net框架，除了EF还有很多很多......

文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

编程新知 2025/8/22 3:26:26

最新SpringBoot+SpringCloud+Nacos微服务框架分享

文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的&#xff0c;根据Excel列的需求预估的工时直接打骨折&#xff0c;不要问我为什么&#xff0c;主要…...

编程新知 2025/8/22 5:05:14

macOS多出来了：Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用

文章目录 问题现象问题原因解决办法 问题现象 macOS启动台&#xff08;Launchpad&#xff09;多出来了&#xff1a;Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显&#xff0c;都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

编程新知 2025/8/18 23:22:02

基础测试工具使用经验

背景 vtune&#xff0c;perf, nsight system等基础测试工具&#xff0c;都是用过的&#xff0c;但是没有记录&#xff0c;都逐渐忘了。所以写这篇博客总结记录一下&#xff0c;只要以后发现新的用法&#xff0c;就记得来编辑补充一下 perf 比较基础的用法&#xff1a; 先改这…...

编程新知 2025/6/17 3:13:49

学习STC51单片机31（芯片为STC89C52RCRC）OLED显示屏1

每日一言 生活的美好&#xff0c;总是藏在那些你咬牙坚持的日子里。 硬件&#xff1a;OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写&#xff0c;"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

编程新知 2025/8/22 14:43:56

视频字幕质量评估的大规模细粒度基准

大家读完觉得有帮助记得关注和点赞&#xff01;&#xff01;&#xff01; 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用&#xff0c;因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型&#xff08;VLMs&#xff09;在字幕生成方面…...

编程新知 2025/8/17 16:33:04

Axios请求超时重发机制

Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式&#xff1a; 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

编程新知 2025/7/21 22:01:13

Webpack性能优化：构建速度与体积优化策略

一、构建速度优化 1、​​升级Webpack和Node.js​​ ​​优化效果​​&#xff1a;Webpack 4比Webpack 3构建时间降低60%-98%。​​原因​​&#xff1a; V8引擎优化&#xff08;for of替代forEach、Map/Set替代Object&#xff09;。默认使用更快的md4哈希算法。AST直接从Loa…...

编程新知 2025/7/7 1:01:12

NPOI Excel用OLE对象的形式插入文件附件以及插入图片

static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

编程新知 2025/7/9 9:17:56