机器学习——多元线性回归升维
机器学习升维
- 升维
- 使用sklearn库实现特征升维
- 实现天猫年度销量预测
- 实现中国人寿保险预测
升维
定义:将原始的数据表示从低维空间映射到高维空间。在线性回归中,升维通常是通过引入额外的特征来实现的,目的是为了更好地捕捉数据的复杂性,特别是当数据之间的关系是非线性的时候。
目的:解决欠拟合问题,提高模型的准确率。为解决因对预测结果考虑因素比较少,而无法准确计算出模型参数问题。
常用方法:将已知维度进行自乘(或相乘)来构建新的维度。
本文主要记录的是线性回归中遇到数据呈现非线性特征时,该如何处理!
切记:对训练集特征升维后也要对测试集、验证集特征数据进行升维操作
数据准备如下:

如果对其直接进行线性回归,则拟合后的模型如下:

从上述两图可知,对于具有非线性特征的图像,不对其使用特使的处理,则无法对其产生比较好的模型拟合。
上述图像生成代码:
# 导包
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# 创建数据
X = np.linspace(-1,11,100)
y = (X - 5)**2 + 3*X + 12 + np.random.randn(100)
X = X.reshape(-1,1)
# display(X.shape,y.shape)
plt.scatter(X,y)# 不升维直接用线性回归解决
model = LinearRegression()
model.fit(X,y)
X_test = np.linspace(-2,12,300).reshape(-1,1)
y_test = model.predict(X_test)
plt.scatter(X,y)
plt.plot(X_test,y_test,color = 'red')
为了使得可以对具有非线性特征的数据进行处理,生成一个较好的模型,可是实现预测的任务,于是便有了升维操作,下举例升维和不升维的区别:
不升维:二维数据x1, x2若不对其进行升维操作,则其拟合的多元线性回归公式为:
y = w 1 ∗ x 1 + w 2 ∗ x 2 + w 0 y = w_1*x_1 + w_2*x_2 + w_0 y=w1∗x1+w2∗x2+w0
升维:若对二维数据x1,x2进行升维操作,则其可有5个维度(以自乘为例):x1、x2、x12,x22、x1*x2,在加上一个偏置项w0,一共有六个参数,则其拟合后的多元线性回归公式为:
y = w 0 + w 1 ∗ x 1 + w 2 ∗ x 2 + w 3 ∗ x 1 2 + w 4 ∗ x 2 2 + w 5 ∗ x 1 ∗ x 2 y= w_0+w_1*x_1+w_2*x_2+w_3*x_1^2+w_4*x_2^2+w_5*x_1*x_2 y=w0+w1∗x1+w2∗x2+w3∗x12+w4∗x22+w5∗x1∗x2
若这样,则由原本的一维线性方程转换成了二维函数(最直观的表现),则原本的数据集则可以拟合成下图所示的模型:

上图生成代码如下:
# 导包
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
X = np.linspace(-1,11,100)
y = (X - 5)**2 + 3*X + 12 + np.random.randn(100)
X = X.reshape(-1,1)# 升维,可以解决多项式的问题,直观表现为可以让直线进行拐弯
np.set_printoptions(suppress=True)
X2 = np.concatenate([X,X**2], axis= 1)
# 注:只需要对特征进行升维,不需要对目标值进行升维# 生成测试数据
X_test = np.linspace(-2,12,300).reshape(-1,1)
model2 = LinearRegression()
model2.fit(X2,y)
X_test2 = np.concatenate([X_test,X_test**2],axis=1)
y_test2 = model2.predict(X_test2)
print('所求的w是\n',model2.coef_)
print('所求的截距b是\n',model2.intercept_)# 绘制图像的时候要用没升维的数据进行绘制
plt.scatter(X,y,color='green')
plt.plot(X_test,y_test2,color = 'red')
使用sklearn库实现特征升维
在sklearn中具有很多封装好的工具,可以直接调用。
from sklearn.preprocessing import PolynomialFeatures # (多项式)升维的python库
使用方法:
# 特征和特征之间相乘
poly = PolynomialFeatures(interaction_only=True)
A = [[3,2]]
poly.fit_transform(A)
# 生成结果:array([[1., 3., 2., 6.]])#特征之间乘法,自己和自己自乘(在上述情况下加上自己的乘法)
poly = PolynomialFeatures(interaction_only=False)
A = [[3,2,5]]
poly.fit_transform(A)
# 生成结果:array([[ 1., 3., 2., 5., 9., 6., 15., 4., 10., 25.]])# 可以通过degree来提高升维的大小
poly = PolynomialFeatures(degree=4,interaction_only=False)# 特征和特征之间相乘
A = [[3,2,5]]
poly.fit_transform(A)
# 生成结果:
# array([[ 1., 3., 2., 5., 9., 6., 15., 4., 10., 25., 27.,
# 18., 45., 12., 30., 75., 8., 20., 50., 125., 81., 54.,
# 135., 36., 90., 225., 24., 60., 150., 375., 16., 40., 100.,
# 250., 625.]])
实现天猫年度销量预测
实现代码:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures,StandardScaler
from sklearn.linear_model import LinearRegression,SGDRegressor# 创建数据
X = np.arange(2009,2020).reshape(-1,1) - 2008
y = np.array([0.5,9.36,52,191,350,571,912,1207,1682,2135,2684])
plt.scatter(X,y)
# 创建测试数据
X_test = np.linspace(2009,2020,100).reshape(-1,1) - 2008# 数据升维
ploy = PolynomialFeatures(degree=2, interaction_only=False)
X2 = ploy.fit_transform(X)
X_test2 = ploy.fit_transform(X_test)# 模型创建LinearRegression
model = LinearRegression(fit_intercept=False)
model.fit(X2,y)
y_pred = model.predict(X_test2)
print('参数w为:',model.coef_)
print('参数b为:',model.intercept_)plt.scatter(X,y,color='green')
plt.plot(X_test,y_pred,color='red')
# 使用SGD进行梯度下降,必须要归一化,否则效果会非常不好
# 创建测试数据
X_test = np.linspace(2009,2019,100).reshape(-1,1) - 2008# 数据升维
ploy = PolynomialFeatures(degree=2, interaction_only=False)
X2 = ploy.fit_transform(X)
X_test2 = ploy.fit_transform(X_test)#对数据进行归一化操作
standard = StandardScaler()
X2_norm = standard.fit_transform(X2)
X_test2_norm = standard.fit_transform(X_test2)# 模型创建SGDRegression
model = SGDRegressor(eta0=0.3, max_iter=5000)
model.fit(X2_norm,y)
y_pred = model.predict(X_test2_norm)
print('参数w为:',model.coef_)
print('参数b为:',model.intercept_)plt.scatter(X,y,color='green')
plt.plot(X_test,y_pred,color='red')
这里需要说明一下情况,如果第二段代码不进行归一化,则呈现的是下图:

如果进行了归一化,则产生的和法一LinearRegession是一样的图形(基本相同):

这是什么原因?
- 线性回归(Linear Regression)和随机梯度下降(SGD)在处理特征尺度不同的问题上有一些不同之处,导致线性回归相对于特征尺度的敏感性较低。
- SGD的更新规则涉及学习率(η)和梯度。如果不同特征的尺度相差很大,梯度的大小也会受到这种尺度差异的影响。因此在引入高次项或其他非线性特征,需要注意特征的尺度,避免数值上的不稳定性。
- SGD中的正则化项通常依赖于权重的大小。通过归一化,可以使得正则化项对所有特征的影响更加平衡。
实现中国人寿保险预测
import pandas as pd
import seaborn as sns
import numpy as np
from sklearn.linear_model import LinearRegression,ElasticNet
from sklearn.metrics import mean_squared_error,mean_squared_log_error
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import PolynomialFeatures# 读取数据
data_renshou = pd.read_excel('your_path/中国人寿.xlsx')
# 可以通过下式生成图像,查看那些数据是好数据那些是不好的数据——好特征:差别大,容易区分
#sns.kdeplot(data=data_renshou, x="charges",hue="sex",shade=True)
#sns.kdeplot(data=data_renshou, x="charges",hue="smoker",shade=True)
#sns.kdeplot(data=data_renshou, x="charges",hue="region",shade=True)
#sns.kdeplot(data=data_renshou, x="charges",hue="children",shade=True)# 特征工程,对数据进行处理
data_renshou = data_renshou.drop(['region','sex'],axis = 1) # 删除不好的特征# 体重指数,离散化转换,体重两种情况:标准,fat
def conver(df,bmi):df['bmi'] = 'fat' if df['bmi'] >= bmi else 'standard'return df
data_renshou = data_renshou.apply(conver, axis=1,args=(30,))# 特征提取,离散转数值型数据
data_renshou = pd.get_dummies(data_renshou)
data_renshou.head()#特征和目标值提取
# 训练数据
x = data_renshou.drop('charges', axis=1)
# 目标值
y = data_renshou['charges']# 划分数据
X_train,X_test,y_train,y_test = train_test_split(x,y,test_size=0.2)# 特征升维(导致了他下面的参数biandu)
poly = PolynomialFeatures(degree=2, include_bias=False)
X_train_poly = poly.fit_transform(X_train)
X_test_poly = poly.fit_transform(X_test)
# 模型训练与评估
np.set_printoptions(suppress=True)
model = LinearRegression()
model.fit(X_train_poly,y_train)
print('测试数据得分:',model.score(X_train_poly,y_train))
print('预测数据得分:',model.score(X_test_poly,y_test))
print('测试数据均方误差:',np.sqrt(mean_squared_error(y_test,model.predict(X_test_poly))))
print('训练数据均方误差:',np.sqrt(mean_squared_error(y_train,model.predict(X_train_poly))))
print('测试数据对数误差:',np.sqrt(mean_squared_log_error(y_test,model.predict(X_test_poly))))
print('训练数据对数误差:',np.sqrt(mean_squared_log_error(y_train,model.predict(X_train_poly))))
print('获得的参数为:',model.coef_.round(2),model.intercept_.round(2))
相关文章:

机器学习——多元线性回归升维
机器学习升维 升维使用sklearn库实现特征升维实现天猫年度销量预测实现中国人寿保险预测 升维 定义:将原始的数据表示从低维空间映射到高维空间。在线性回归中,升维通常是通过引入额外的特征来实现的,目的是为了更好地捕捉数据的复杂性&#…...
[C/C++]用堆实现TopK算法
一:引入 思考一个问题: 怎么在100个数中找到前10个最大的数? way1: 相信大多数人想到的方法是先把100个数放到数组中从大到小排序,再打印前10个数 way2: 前一文中我们讲了堆结构,那么就可以把这100个数建为大堆,再依次pop10次 这种方法虽然再这个问题下可行,但是如果是再1亿…...
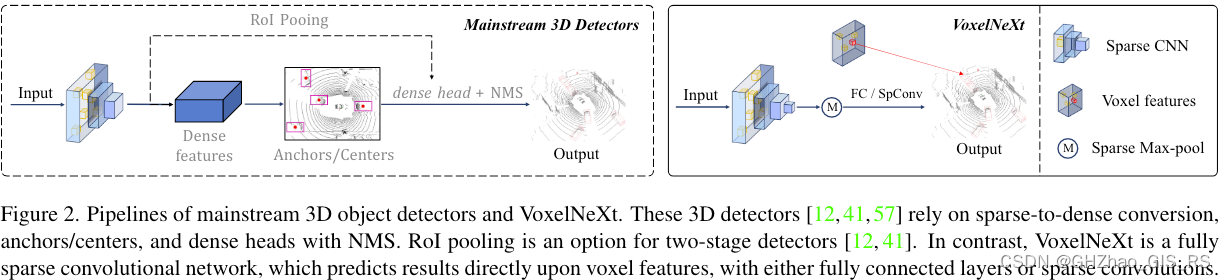
3D点云目标检测:VoxelNex解读(带源码/未完)
VoxelNext 通用vsVoxelNext一、3D稀疏卷积模块1.1、额外的两次下采样1.2、稀疏体素删减 二、高度压缩三、稀疏池化四、head五、waymo数据集训练六、训练自己的数据集bug修改 通用vsVoxelNext 一、3D稀疏卷积模块 1.1、额外的两次下采样 使用通用的3D sparse conv,…...
【Docker】从零开始:11.Harbor搭建企业镜像仓库
【Docker】从零开始:11.Harbor搭建企业镜像仓库 1. Harbor介绍2. 软硬件要求(1). 硬件要求(2). 软件要求 3.Harbor优势4.Harbor的误区5.Harbor的几种安装方式6.在线安装(1).安装composer(2).配置内核参数,开启路由转发(3).下载安装包并解压(4).创建并修改配置文件(5…...

使用conan包 - 工作流程
使用conan包 - 工作流程 主目录 conan Using packages1 Single configuration2 Multi configuration 本文是基于对conan官方文档Workflows的翻译而来, 更详细的信息可以去查阅conan官方文档。 This section shows how to setup your project and manage dependenci…...

【LeeCode】59.螺旋矩阵II
给定一个正整数 n,生成一个包含 1 到 n^2 所有元素,且元素按顺时针顺序螺旋排列的正方形矩阵。 示例: 输入: 3 输出: [ [ 1, 2, 3 ], [ 8, 9, 4 ], [ 7, 6, 5 ] ] 解: class Solution {public int[][] generateMatrix(int n) {int[][] ar…...
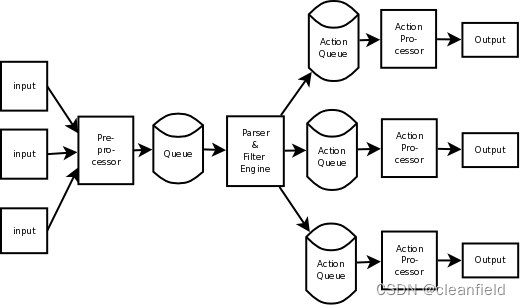
rsyslog学习
rsyslog是什么 RSYSLOG(Remote System Logging)是一个开源的日志处理工具,用于在 Linux 和 Unix 系统上收集、处理和转发日志。它是一个健壮且高性能的日志处理程序,可以替换 Syslogd 作为标准的系统日志程序。RSYSLOG 提供了许多…...
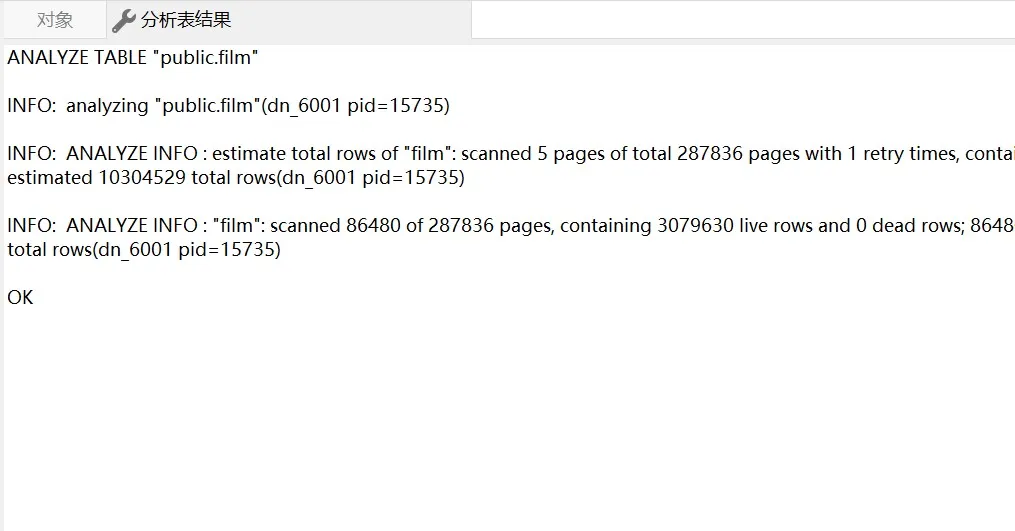
Navicat 技术指引 | GaussDB服务器对象的创建/设计(编辑)
Navicat Premium(16.2.8 Windows版或以上) 已支持对GaussDB 主备版的管理和开发功能。它不仅具备轻松、便捷的可视化数据查看和编辑功能,还提供强大的高阶功能(如模型、结构同步、协同合作、数据迁移等),这…...

有哪些可信的SSL证书颁发机构?
目前市面上所显示的SSL证书颁发机构可所谓不计其数,类型也是多样,就好比我们同样是买一件T恤,却有百家不同类型的店铺一个道理。根据CA里面看似很多,但能拿到99%浏览器及设备信任度的寥寥无几,下面小编整理出几家靠谱可…...
MidJourney笔记(4)-settings
前面已经大概介绍了MidJourney的基础知识,后面我主要是基于实操来分享自己的笔记。可能内容顺序会有点乱,请大家理解。 这次主要是想讲讲settings这个命令。我们只需在控制台输入/settings,然后回车,就可以执行这个命令。 (2023年11月26日版本界面) 可能有些朋友出来的界…...
前端开发学习 (三) 列表功能
一、列表功能 1、列表功能 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><meta http-equiv"X-UA-Compa…...
win11渗透武器库,囊括所有渗透工具
开箱即用,最全的武器库,且都是2023年11月最新版,后续自己还可以再添加,下载地址:https://download.csdn.net/download/weixin_59679023/88565739 服务连接 信息收集工具 端口扫描 代理抓包 漏洞扫描 指纹识别 webshel…...

13-21-普通数组、矩阵
LeetCode 热题 100 文章目录 LeetCode 热题 100普通数组13. 中等-最大子数组和14. 中等-合并区间15. 中等-轮转数组16. 中等-除自身以外数组的乘积17. 困难-缺失的第一个正数 矩阵18. 中等-矩阵置零19. 中等-螺旋矩阵20. 中等-旋转图像21. 中等-搜索二维矩阵II 本文存储我刷题的…...
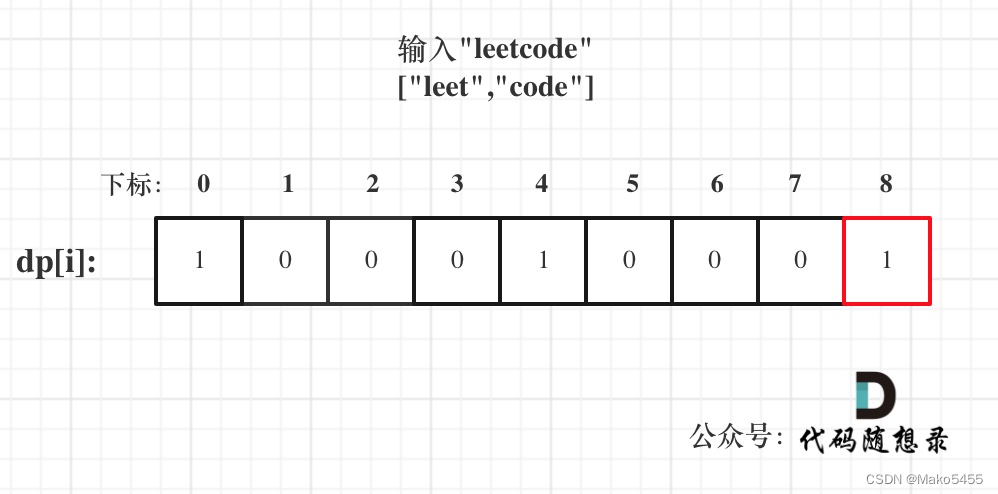
代码随想录算法训练营第四十六天【动态规划part08】 | 139.单词拆分、背包总结
139.单词拆分 题目链接: 力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 求解思路: 单词是物品,字符串s是背包,单词能否组成字符串s,就是问物品能不能把背包装满。 动规五部曲 确定dp数…...

go语言基础 break和contine区别
背景 break和continue是编程语言的标准语法,几乎在所有的语言都有类似的用法。 go语言及所有其他编程语言for循环或者其他循环 区别 for i : 0; i < 10; i {if i 5 {continue}fmt.Println(i)for j : 0; j < 3; j {fmt.Println(strconv.Itoa(j) "a&q…...
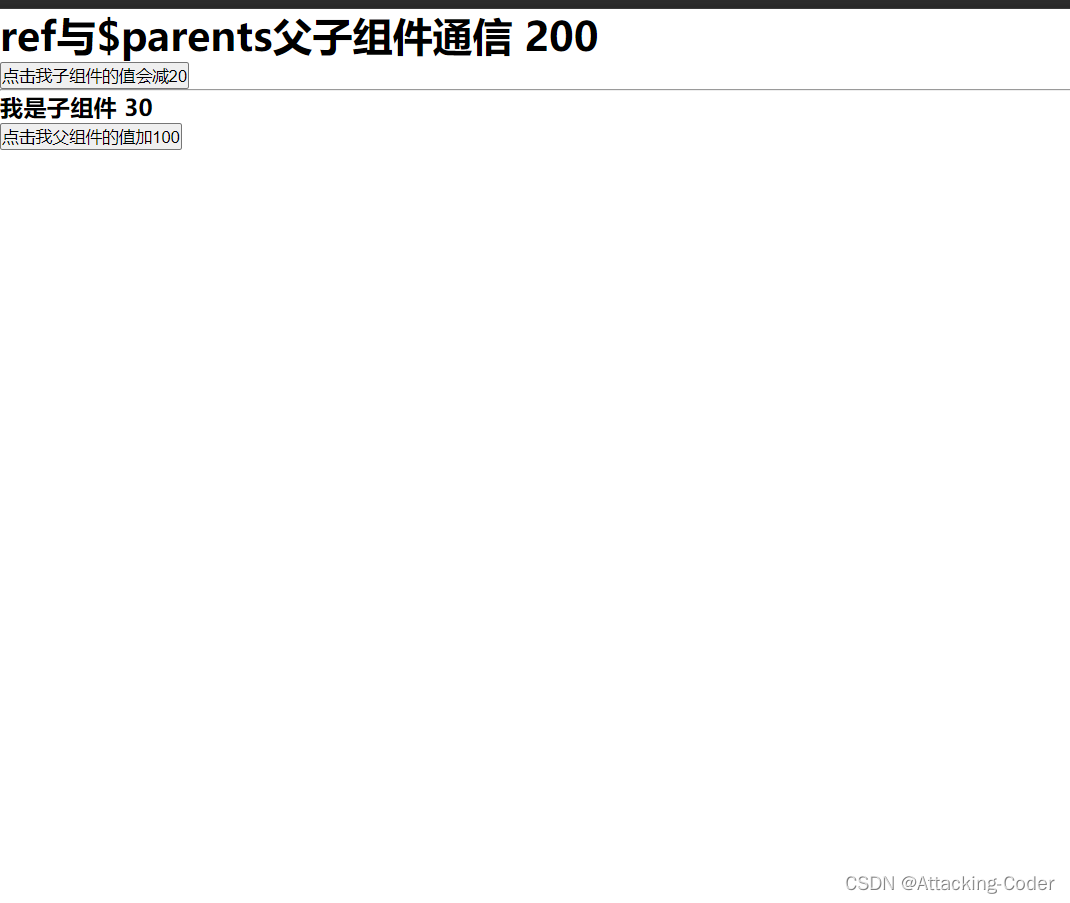
vue3父子组件通过$parent与ref通信
父组件 <template><div><h1>ref与$parents父子组件通信 {{ parentMoney }}</h1><button click"handler">点击我子组件的值会减20</button><hr><child ref"children"></child></div> </te…...

PHP中的常见的超全局变量
PHP是一种广泛使用的服务器端脚本语言,它被用于开发各种Web应用程序。在PHP中,有一些特殊的全局变量,被称为超全局变量。超全局变量在整个脚本中都是可用的,无需使用global关键字来访问它们。在本文中,我们将深入了解P…...
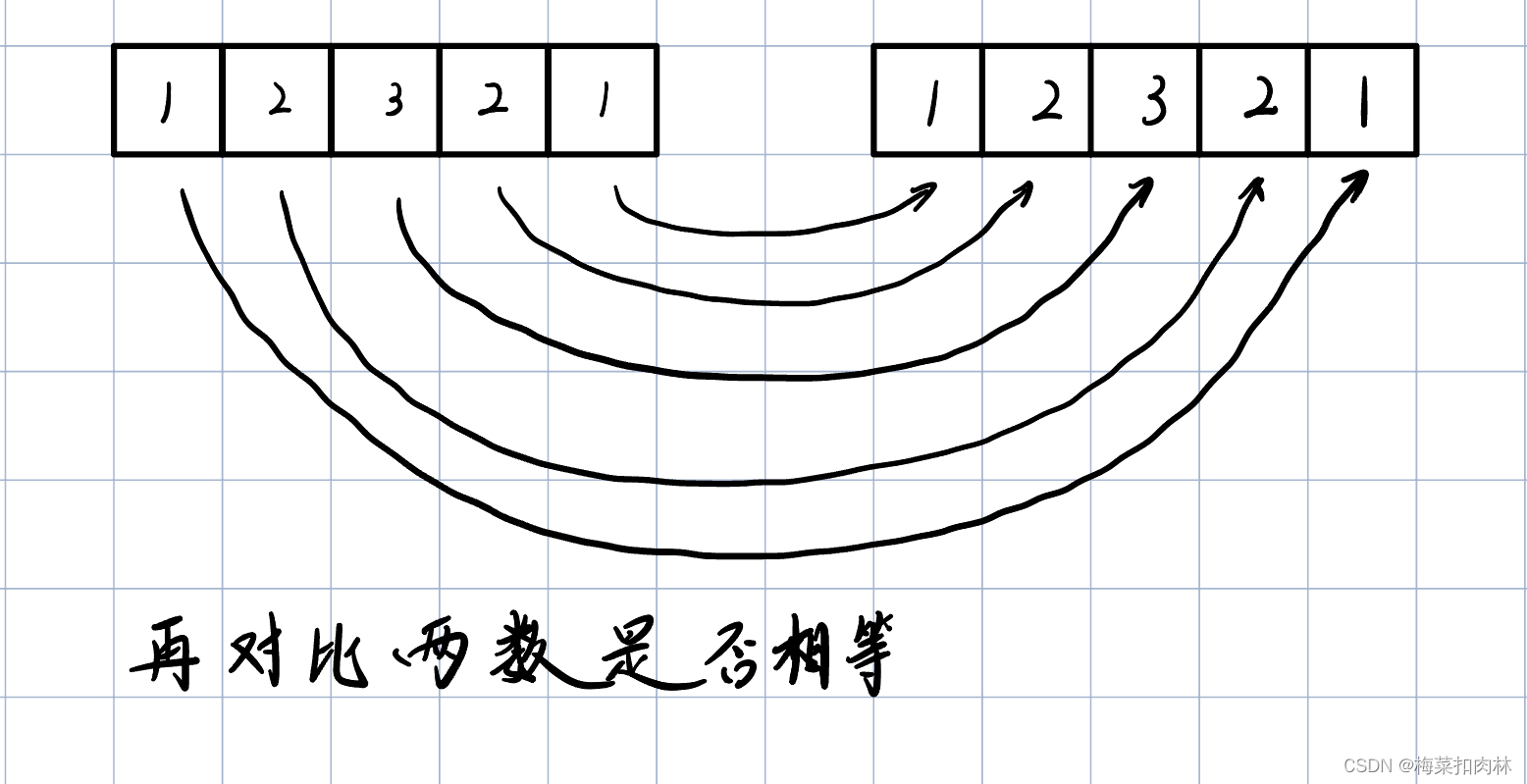
leetcode9.回文数
回文数 0.题目1.WJQ的思路2.实现过程2.0 原始值怎么一个个取出来?2.1 取出来的数如何存到新的数字后面?2.2完整的反转得到新数的过程 3.完整的代码4.可运行的代码5.算法还可以优化的部分 0.题目 给你一个整数 x ,如果 x 是一个回文整数&…...
)
springboot(ssm大学生二手电子产品交易平台 跳蚤市场系统Java(codeLW)
springboot(ssm大学生二手电子产品交易平台 跳蚤市场系统Java(code&LW) 开发语言:Java 框架:ssm/springboot vue JDK版本:JDK1.8(或11) 服务器:tomcat 数据库:mysql 5.7(或…...
关于微信小程序中如何实现数据可视化-echarts动态渲染
移动端设备中,难免会涉及到数据的可视化展示、数据统计等等,本篇主要讲解原生微信小程序中嵌入echarts并进行动态渲染,实现数据可视化功能。 基础使用 首先在GitHub上下载echarts包 地址:https://github.com/ecomfe/echarts-for…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...
