回归分析例题(多元统计分析期末复习)
例一

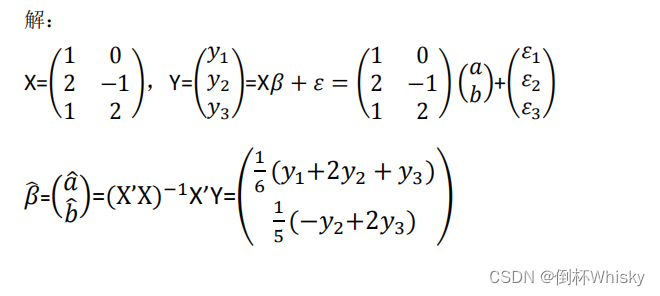
例二
一元线性回归
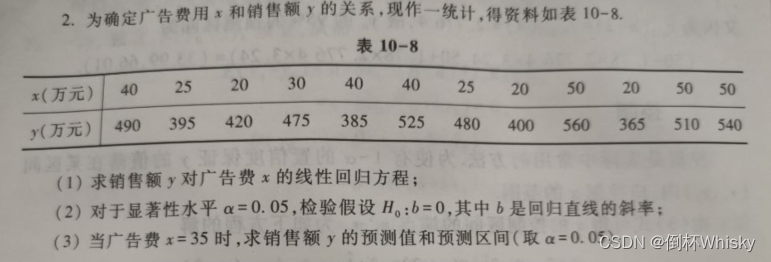
解:
(1)y= a ^ \hat{a} a^+ b ^ \hat{b} b^x,求线性回归方程即求出 a ^ \hat{a} a^和 b ^ \hat{b} b^
而
所以我们首先需要计算 L x y {L_{xy}} Lxy 和 L x x {L_{xx}} Lxx:
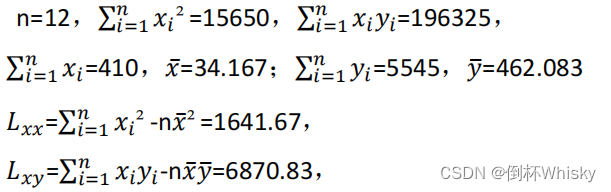
所以 b ^ \hat{b} b^= L x y L x x { {L_{xy}} \over {L_{xx}} } LxxLxy=4.185
a ^ \hat{a} a^= y ˉ \bar{y} yˉ- b ^ x ˉ \hat{b}\bar{x} b^xˉ=319.086
所以回归方程为 y ^ \hat{y} y^=319.086+4.185x
(2)显著性检验需要我们计算出 T 0 {T_0} T0,所以依次计算出 L y y {L_{yy}} Lyy、 σ ^ \hat{σ} σ^,计算得 T 0 {T_0} T0如下:
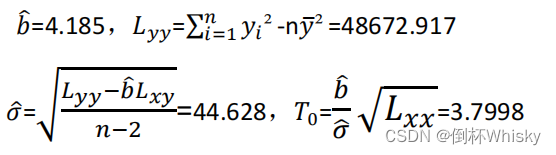
而 F 0 {F_0} F0= T 0 2 {T_0^2} T02=14.438> F α {F_α} Fα(1,n-2)= F 0.05 {F_{0.05}} F0.05(1,10)=4.965,因此拒绝 H 0 {H_0} H0,即:回归效果是显著的。
(3)预测值直接把 x 0 {x_0} x0=35代入回归方程即可, y 0 ^ \hat{y_0} y0^=319.086+4.185*35=465.571;
而预测区间需要计算出以下值:
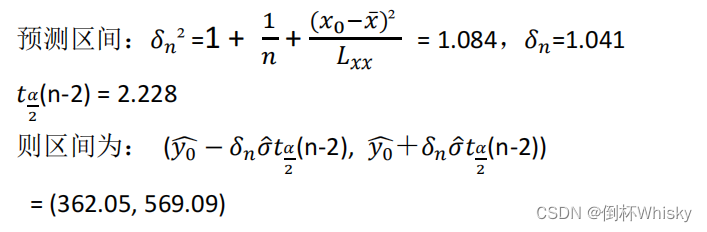
其实难度不大,主要是记住公式就行。
例三
多元线性回归
X= [ 0 0 1 1 1 1 − 1 1 2 0 ] \begin{bmatrix} 0 & 0 \\ 1& 1 \\ 1 &1 \\ -1 &1 \\ 2 & 0 \end{bmatrix} 011−1201110 ,Y= [ 0.01 2.98 3.04 − 1.97 4.96 ] \begin{bmatrix} 0.01 \\ 2.98 \\ 3.04 \\ -1.97 \\ 4.96 \end{bmatrix} 0.012.983.04−1.974.96
设y= β 1 {β_1} β1 x 1 {x_1} x1+ β 2 {β_2} β2 x 2 {x_2} x2+ε 求:
(1)试求β;
(2)Y的预测值 Y ^ \hat{Y} Y^, ε ^ \hat{ε} ε^以及残差平方和Q;
(3)决定系数 R 2 {R^2} R2 和 回归平方和U;
这题可以算是比较典型的一道多元回归了,无论是什么情境下,我们都可以总结出X和Y两个矩阵,题目无非是要我们求β、Q、U和R²,只要记住公式+计算正确一般没什么问题。
解:
求回归方程(Y=Xβ+ε)即 求β和ε,因为X和Y我们可以从题目中总结出来;
首先我们需要求β,记住以下公式:
β = ( X ′ X ) − 1 X ′ Y β={(X'X)^{-1}}X'Y β=(X′X)−1X′Y
X和Y都是已知的,先求X’X,再求其逆矩阵,一般情况下题目给出的都是二阶矩阵,而二阶矩阵的逆矩阵的计算公式为:
A − 1 {A^{-1}} A−1= A ∗ ∣ A ∣ {A^*} \over |A| ∣A∣A∗
即A的伴随矩阵除以A的行列式,而二阶矩阵的伴随矩阵有个口诀是“主交换,副变号”,意思是主对角线的元素对换,副对角线的元素变成其相反数。
所以我们计算得到X’X= [ 7 1 1 3 ] \begin{bmatrix} 7 & 1 \\ 1 & 3 \\ \end{bmatrix} [7113],它的伴随矩阵就是 [ 3 − 1 − 1 7 ] \begin{bmatrix} 3 & -1 \\ -1 & 7 \\ \end{bmatrix} [3−1−17],再除以行列式值为20,所以它的逆矩阵 ( X ′ X ) − 1 {(X'X)^{-1}} (X′X)−1= [ 0.15 − 0.05 − 0.05 0.35 ] \begin{bmatrix} 0.15 & -0.05 \\ -0.05 & 0.35 \\ \end{bmatrix} [0.15−0.05−0.050.35]
接着再依次乘上X’、Y,最终结果为
β = [ 2.484 0.522 ] β=\begin{bmatrix} 2.484 \\ 0.522 \\ \end{bmatrix} β=[2.4840.522]
于是我们就可以把 Y的预测值 计算出来,
Y ^ \hat{Y} Y^=Xβ= [ 0 0 1 1 1 1 − 1 1 2 0 ] \begin{bmatrix} 0 & 0 \\ 1& 1 \\ 1 &1 \\ -1 &1 \\ 2 & 0 \end{bmatrix} 011−1201110 [ 2.484 0.522 ] \begin{bmatrix} 2.484 \\ 0.522 \\ \end{bmatrix} [2.4840.522]= [ 0 3.006 3.006 − 1.962 4.968 ] \begin{bmatrix} 0 \\ 3.006 \\ 3.006\\ -1.962 \\ 4.968 \end{bmatrix} 03.0063.006−1.9624.968
ε ^ \hat{ε} ε^= Y {Y} Y- Y ^ \hat{Y} Y^= [ 0.01 − 0.026 0.034 − 0.008 − 0.008 ] \begin{bmatrix} 0.01\\ -0.026 \\ 0.034\\ -0.008 \\ -0.008 \end{bmatrix} 0.01−0.0260.034−0.008−0.008
残差平方和Q 就是 ε ^ \hat{ε} ε^中元素的平方和,即:
Q= ε ^ \hat{ε} ε^' ε ^ \hat{ε} ε^=0.00206
接下来计算 回归平方和U,等于总偏差平方和-残差平方和
通过矩阵Y和Y的均值 Y ˉ \bar{Y} Yˉ我们可以首先把总偏差平方和算出来
TSS=( Y − Y ˉ Y-\bar{Y} Y−Yˉ)'( Y − Y ˉ Y-\bar{Y} Y−Yˉ)
或TSS= Y ′ Y Y'Y Y′Y-n Y 2 ˉ \bar{Y^2} Y2ˉ
用第一个式子算出TSS=30.33252
所以U=TSS-Q=30.33046
决定系数 为
R 2 = U T S S {R^2}={U \over TSS} R2=TSSU
所以 R 2 {R^2} R2=30.33046/30.33252=0.999932
相关文章:
回归分析例题(多元统计分析期末复习)
例一 例二 一元线性回归 解: (1)y a ^ \hat{a} a^ b ^ \hat{b} b^x,求线性回归方程即求出 a ^ \hat{a} a^和 b ^ \hat{b} b^ 而 b ^ \hat{b} b^ L x y L x x { {L_{xy}} \over {L_{xx}} } LxxLxy 所以我们首先需要计算 L x…...
Linux多路转接select,poll
文章目录 目录 文章目录 一、五种IO模型 1.阻塞IO: 2.非阻塞IO 3.信号驱动IO 4.IO多路转接 5.异步IO 二、高级IO的一些重要概念 1.同步通信和异步通信 2.阻塞和非阻塞 三、其他高级IO 四、非阻塞IO 1.fctl函数 2.实现setNoBlock函数,将文件描述符设置…...
如何轻松将 4K 转换为 1080p 高清视频
由于某些原因,你可能有一些 4K 视频,与1080p、1080i、720p、720i等高清视频相比,4K 视频具有更高的分辨率,可以给您带来更多的视觉和听觉享受。但是,播放4k 视频是不太容易的,因为超高清电视没有高清电视那…...
)
责任链模式 (Chain of Responsibility Pattern)
定义 责任链模式是一种行为型设计模式,用于在对象间建立一条处理请求的链。它允许多个对象有机会处理请求,从而减少请求的发送者和接收者之间的耦合。在责任链模式中,每个接收者包含对另一个接收者的引用,形成一条链。如果一个对…...
企业营销管理能够实现自动化吗?怎么做?
当今企业面临着越来越多的营销难题:如何有效培育潜在客户、如何提高营销活动的效果、如何优化营销资源的分配......企业的营销管理怎么做?或许CRM系统营销自动化会起到作用。 客户细分: 企业可以通过CRM的客户细分功能,根据客户…...
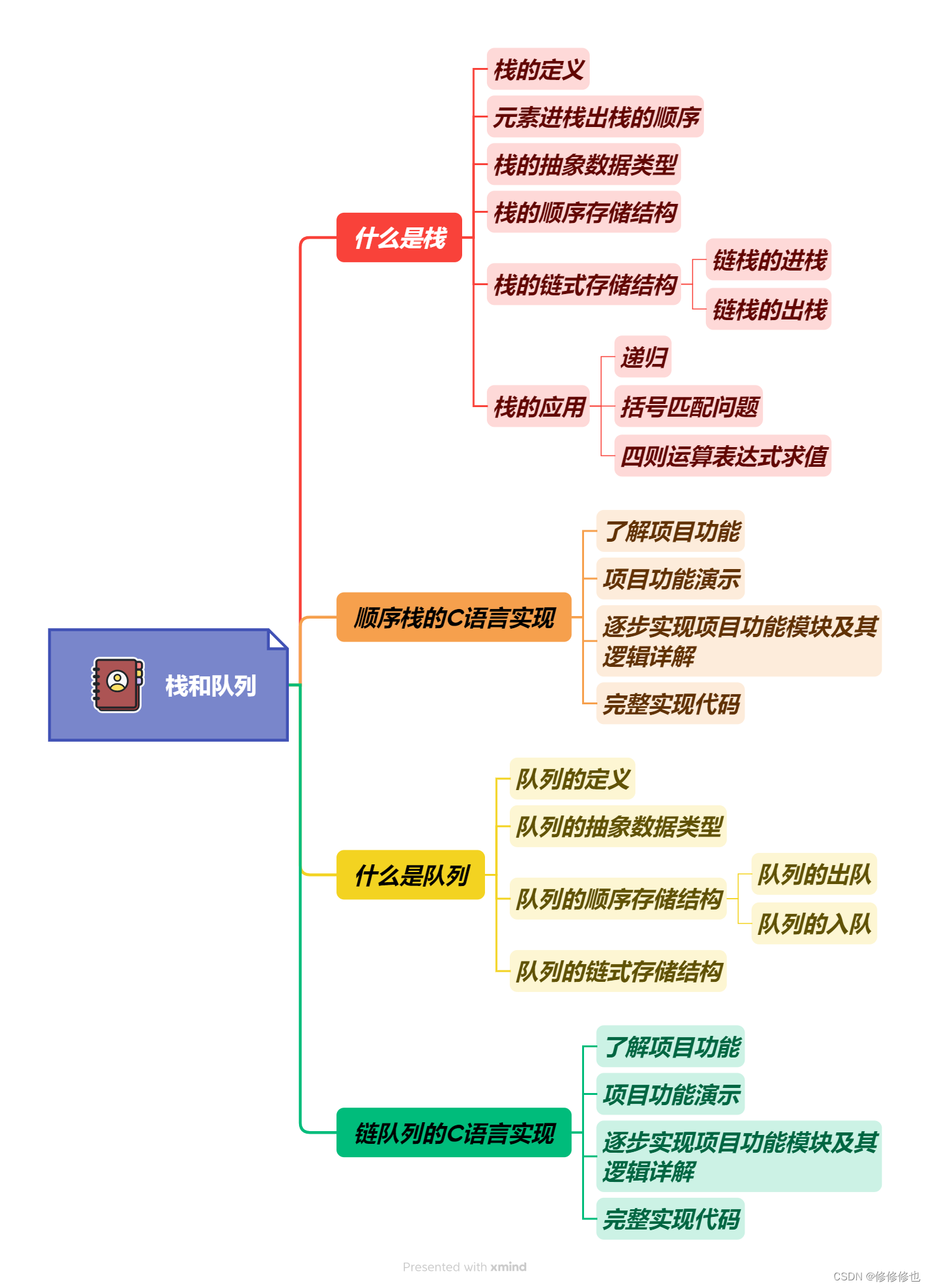
【数据结构】什么是栈?
🦄个人主页:修修修也 🎏所属专栏:数据结构 ⚙️操作环境:Visual Studio 2022 目录 📌栈的定义 📌元素进栈出栈的顺序 📌栈的抽象数据类型 📌栈的顺序存储结构 📌栈的链式存储结构 链栈的进…...
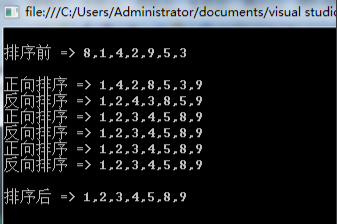
基于C#实现鸡尾酒排序(双向冒泡排序)
通俗易懂点的话,就叫“双向冒泡排序”。 冒泡是一个单向的从小到大或者从大到小的交换排序,而鸡尾酒排序是双向的,从一端进行从小到大排序,从另一端进行从大到小排序。 从图中可以看到,第一次正向比较,我们…...
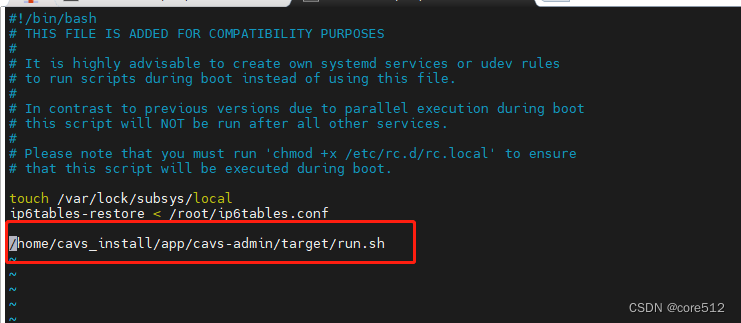
CentOS添加开机启动
1.编写项目启动脚本(run.sh) #!/bin/bash-切换到程序所在路径 cd /home/cavs_install/app/cavs-admin/target/ # 等待其他组件启动完毕后再启动本项目(如果不需要等待,本步骤可省略) sleep 300 # 实际启动命令 nohup …...
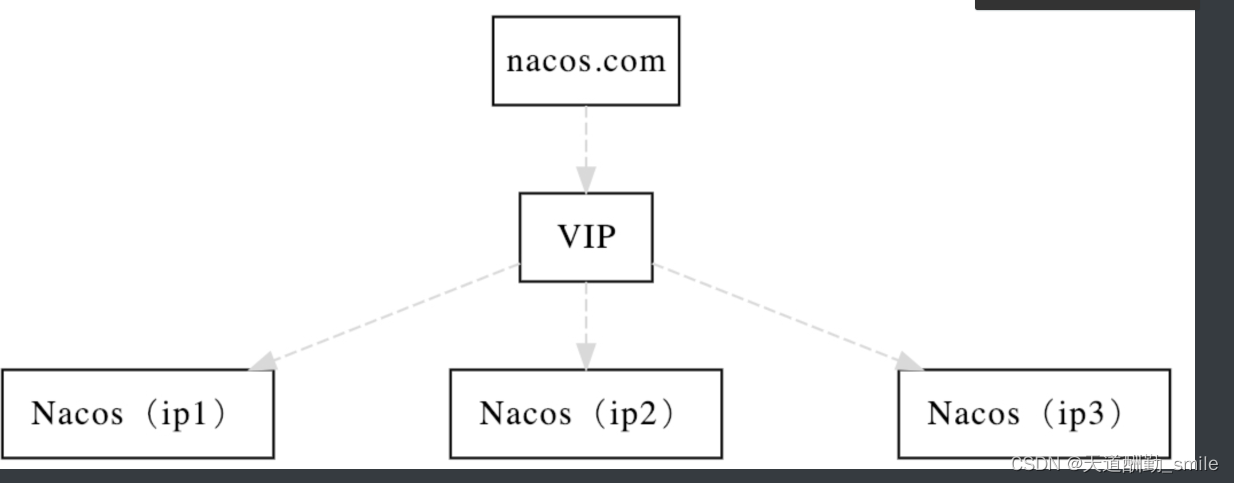
SpringCloudAlibaba之Nacos的持久化和高可用——详细讲解
目录 一、Nacos持久化 1.持久化说明 2.安装mysql数据库5.6.5以上版本(略) 3.修改配置文件 二、nacos高可用 1.集群说明 2.nacos集群架构图 2.集群搭建注意事项 3.集群规划 4.搭建nacos集群 5.安装Nginx 6.配置nginx conf配置文件 7.启动nginx进行测试即可 一、Nacos持久…...
vue3安装eslint和prettier,最简单的步骤
第1步: 安装eslint yarn add eslint -D 第2步: 在根文件夹中,创建.eslintrc.js文件 第3步: 在package.json文件中新增命令 "lint": "eslint --fix --ext .ts,.tsx,.vue src --quiet","prettier"…...

Day32| Leetcode 122. 买卖股票的最佳时机 II Leetcode 55. 跳跃游戏 Leetcode 45. 跳跃游戏 II
Leetcode 122. 买卖股票的最佳时机 II 题目链接 122 买卖股票的最佳时机 II 本题目设计的还是比较巧妙的,把最终的利润分为每天的利润就解决了(贪心),每天的利润就是前一天买进,后一天卖出,转化到代码上就…...
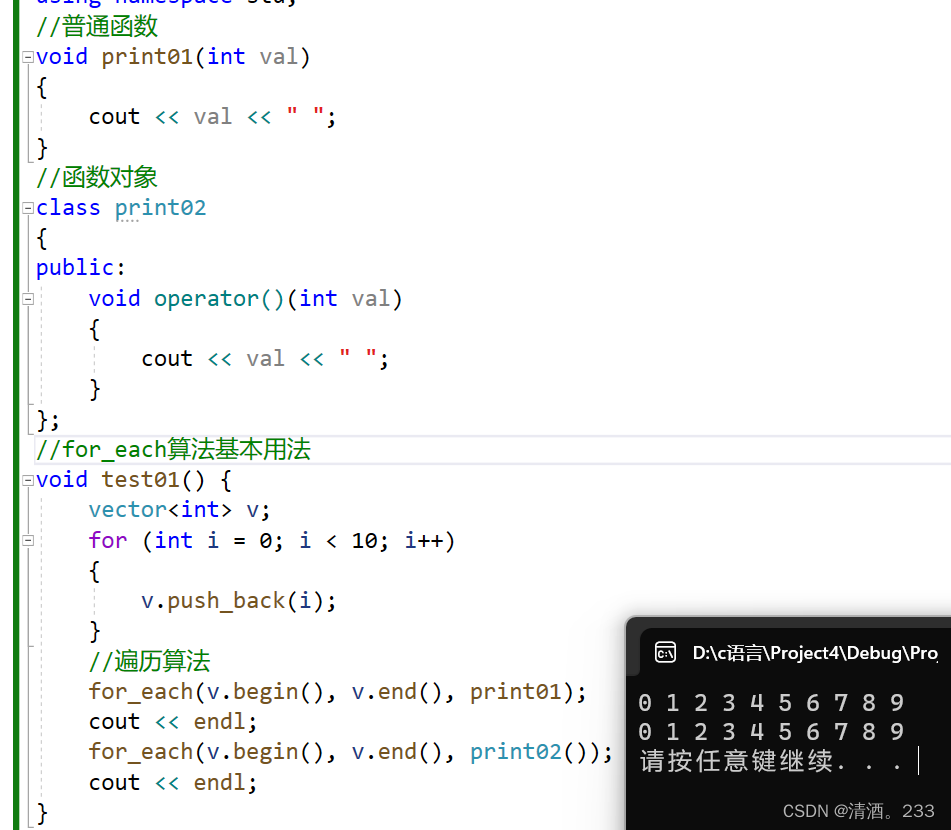
95.STL-遍历算法 for_each
算法概述: 算法主要是由头文件 <algorithm> <functional> <numeric> 组成。 <algorithm> 是所有STL头文件中最大的一个,范围涉及到比较、 交换、查找、遍历操作、复制、修改等等 <numeric> 体积很小,只包括几个在序列上面…...

Python基础语法之学习type()函数
Python基础语法之学习type函数 一、代码二、效果 查看数据类型或者说查看变量存储的数据类型 一、代码 print(type("文本")) print(type(666)) print(type(3.14))二、效果 梦想是生活的指南针,坚持追逐梦想,终将抵达成功的彼岸。不要害怕失败…...

filebeat报错dropping too large message of size
filebeat报错: dropping too large message of size 1714620. 原因: kafka对每一条消息的大小进行了限制。 解决 kafka端 修改config/server.properties,添加以下配置 max_message_bytes10000000 replica.fetch.max.bytes10000000修改…...
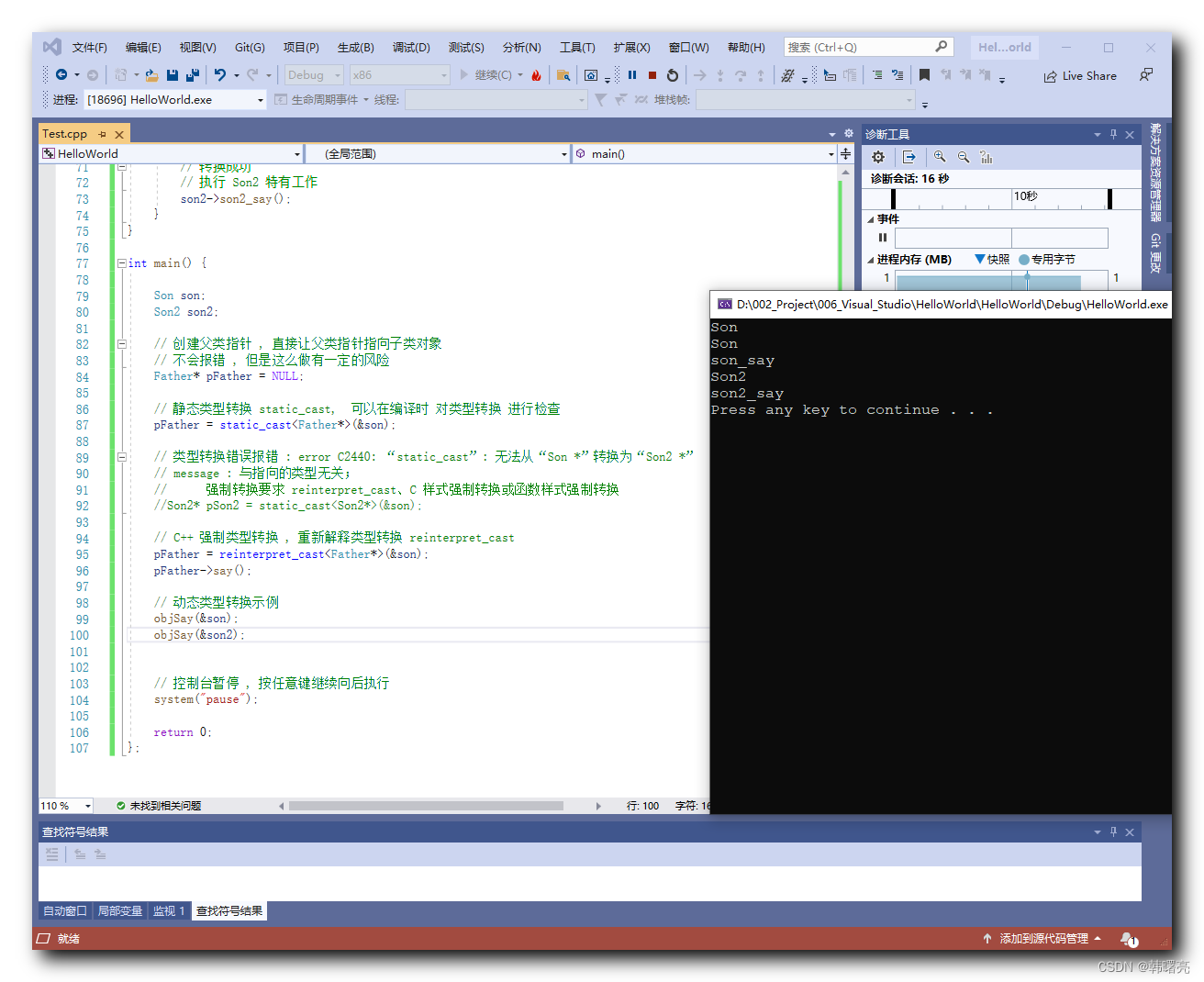
【C++】类型转换 ④ ( 子类 和 父类 之间的类型转换 - 动态类型转换 dynamic_cast )
文章目录 一、子类 和 父类 之间的类型转换 - 动态类型转换 dynamic_cast1、构造父类和子类2、子类 和 父类 之间的类型转换 - 隐式类型转换3、子类 和 父类 之间的类型转换 - 静态类型转换 static_cast4、子类 和 父类 之间的类型转换 - 重新解释类型转换 reinterpret_cast5、…...

在CentOS 7.9上搭建高性能的FastDFS+Nginx文件服务器集群并实现外部远程访问
文章目录 引言第一部分:FastDFS介绍与安装1.1 FastDFS简介1.2 FastDFS安装1.2.1 安装Tracker Server1.2.2 安装Storage Server 1.3 FastDFS配置1.3.1 配置Tracker Server1.3.2 配置Storage Server1.3.3 启动FastDFS服务 第二部分:Nginx配置2.1 Nginx安装…...
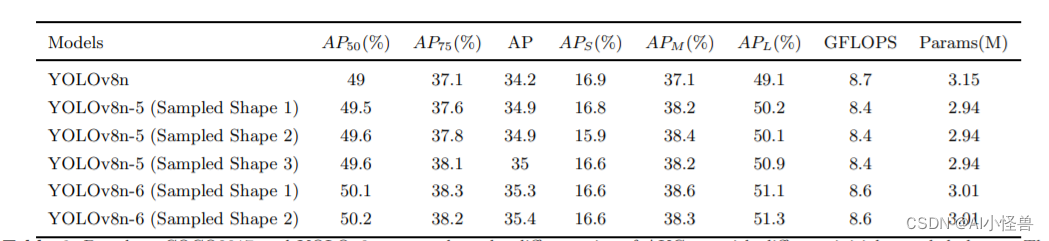
YOLOv8独家原创改进: AKConv(可改变核卷积),即插即用的卷积,效果秒杀DSConv | 2023年11月最新发表
💡💡💡本文全网首发独家改进:可改变核卷积(AKConv),赋予卷积核任意数量的参数和任意采样形状,为网络开销和性能之间的权衡提供更丰富的选择,解决具有固定样本形状和正方形的卷积核不能很好地适应不断变化的目标的问题点,效果秒殺DSConv 1)AKConv替代标准卷积进行…...

Docker pause/unpause命令
docker pause :暂停容器中所有的进程。 docker unpause :恢复容器中所有的进程。 语法 docker pause CONTAINER [CONTAINER...]docker unpause CONTAINER [CONTAINER...]实例 暂停数据库容器db01提供服务。 docker pause db01恢复数据库容器db01提供…...

PostgreSQL create or replace view和重建视图 有什么区别?
一、 replace vs 重建 遇到开发提了个问题,create or replace view和重建视图(dropcreate)有什么区别,查询资料整理了一下。 1. create or replace 当存在同名视图时,尝试将其替换新视图语句必须与现有视图查询具有相…...
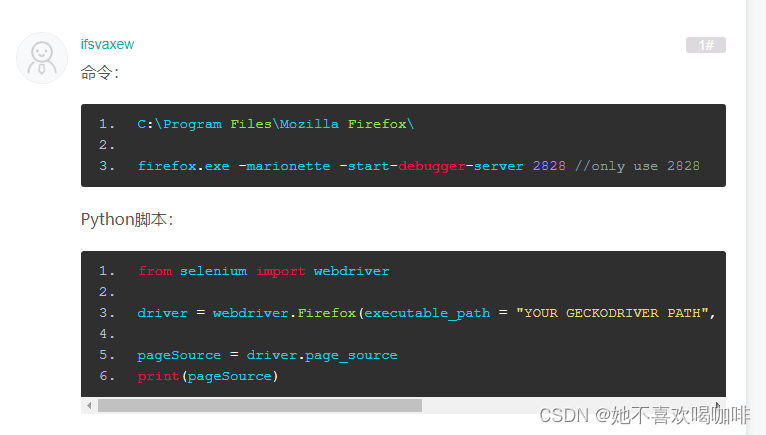
Selenium 连接到现有的 Firefox 示例
当前环境: python 3.7 selenium 3.14.1 urllib3 1.26.8 Frefox 115.1.0esr(32位) geckodriver.exe 0.33.0 1 下载 Firefox 浏览器,根据自己的需要选择。 下载 Firefox 浏览器,这里有简体中文及其他 90 多种语言版本…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...
