【蓝桥杯】刷题
刷题网站
记录总结刷题过程中遇到的一些问题
1、最大公约数与最小公倍数
a,b=map(int,input().split())s=a*bwhile a%b:a,b=b,a%bprint(b,s//b)
2.迭代法求平方根(题号1021)
#include<stdio.h>
#include<math.h>
int main()
{double x1=1.0,x2;int a;scanf("%d",&a);do{x1=x2;x2=(x1+a/x1)/2;}while(fabs(x2-x1)>0.00001);printf("%.3lf",x1);return 0;
}
3、筛选N以内的素数(1022)
采用埃筛法筛选素数
思路是给定一个较大的bool数组,刚开始将其所有元素赋值为True,从2开始,那么2的倍数就一定不是素数,将对应的bool值重新赋值为0,依次,3的倍数也不是素数…
N=int(input())
isprime=[True]*10000
isprime[0]=False
isprime[1]=False
# print(isprime[0:10])
for i in range(2,N):if (isprime[i]==True):index=iwhile index<N:index+=iisprime[index]=0
for i,val in enumerate(isprime[0:N]):if val==True:print(i)
4、求完数(1017)
一个数如果恰好等于不包含它本身所有因子之和,这个数就称为"完数"。 例如,6的因子为1、2、3,而6=1+2+3,因此6是"完数"。
① 这个题最常见的思路是两层循环,依次列举出每一个数的因子并判断
N=int(input())
x=[1]
for i in range(2,N+1):for j in range(2,i):if(i%j)==0:x.append(j)if x !=None:if i==sum(x):print("%d"%i,"its factors are ",end="")print(*x,sep=" ")x=[1]
运行时间超时了。。。。。
② 仔细思考一下,一个数的最小因子就是2(最小是2,也有可能是3、5、7),那么一个数的最大因子不会超过其1/2,所以只需要在某个数的一半找其对应的因子即可
N=int(input())
x=[1]
for i in range(2,N+1):for j in range(2,int(i/2)+1):if(i%j)==0:x.append(j)if x !=None:if i==sum(x):print("%d"%i,"its factors are ",end="")print(*x,sep=" ")x=[1]
运行时间仍然超时
分析:
第一个时间复杂度为 n ∗ n = o ( n 2 ) n*n=o(n^{2} ) n∗n=o(n2)
第二个时间复杂度为 n ∗ ( n 2 ) = o ( ( n 2 ) 2 ) n*(\frac{n}{2})=o((\frac{n}{2})^{2} ) n∗(2n)=o((2n)2)
整体时间复杂度都为
o ( n 2 ) o(n^{2} ) o(n2)
③后面在网上看到了这一招,自己怎么就没想到喃,先上代码
n = int(input())
for i in range(6, n + 1, 2):factors = [1]sqrt_i = int(pow(i,0.5))for j in range(2, sqrt_i + 1):if i % j == 0:factors.append(j)if j != i // j:factors.append(i // j)if sum(factors) == i:print(f"{i} its factors are {' '.join(map(str, sorted(factors)))}")
其实就是先穷举找到 [ 0 , x ] \left [ 0,\sqrt{x} \right ] [0,x]范围内的因子,然后用x整除这些因子,就可以求到 [ x , x ] \left [ \sqrt{x},x \right ] [x,x]范围内的因子
即找全所有因子
计算复杂度可以理解为
o ( n log n ) o(n\log_{}{n} ) o(nlogn)
5、数字后移(1046)
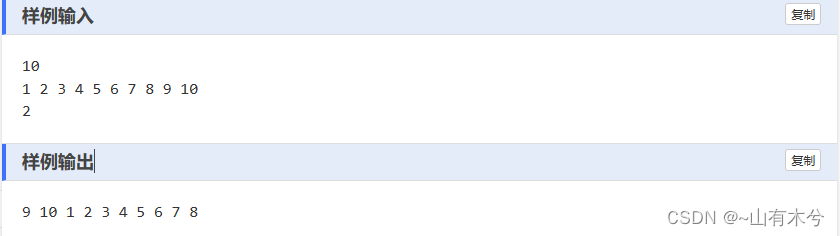
这里题目要求的是一种类似循环数组的方式,核心是取余运算
n=int(input())
x=list(input().split())
y=list(x)
m=int(input())
for i in range(0,n):idx=(i+m)%(n)y[idx]=x[i]
print(*y,sep=" ")
注意:
#指向相同的对象,x,y中的一个改变,另一个都会随之改变
x=list(input().split())
y=x
<<<<<<------------------------>>>>>>
#指向不同的对象,两个互不影响
x=list(input().split())
y=list(x)
相关文章:

【蓝桥杯】刷题
刷题网站 记录总结刷题过程中遇到的一些问题 1、最大公约数与最小公倍数 a,bmap(int,input().split())sa*bwhile a%b:a,bb,a%bprint(b,s//b)2.迭代法求平方根(题号1021) #include<stdio.h> #include<math.h> int main() {double x11.0,x2;int a;scanf("%d&…...

软件产品登记的材料条件
(1)申请双软认证前应该要获得信息产业部授权的软件检测机构出具的检测证明,这份检测证明可以到软件行业协会申请,然后协会会派专家到公司进行“检测”,检测通过后出具证明,这份证明的申请与软件著作权等无关࿰…...

春节后跟进客户开发信模板?外贸邮件模板?
适合新年的客户开发信模板?年后给客户的邮件怎么写? 在春节这一传统的中国节日结束后,跟进客户对于维持和发展业务至关重要。客户开发信模板是一种有效的工具。蜂邮将介绍一些春节后跟进客户开发信模板的关键技巧,以确保您的业务…...

个人财务管理软件CheckBook Pro mac中文版特点介绍
CheckBook Pro mac是一款Mac平台的个人财务管理软件,主要用于跟踪个人收入、支出和账户余额等信息。 CheckBook Pro mac 软件特点 简单易用:该软件的用户界面非常简洁明了,即使您是初学者也可以轻松上手。 多账户管理:该软件支持…...

rfc4301- IP 安全架构
1. 引言 1.1. 文档内容摘要 本文档规定了符合IPsec标准的系统的基本架构。它描述了如何为IP层的流量提供一组安全服务,同时适用于IPv4 [Pos81a] 和 IPv6 [DH98] 环境。本文档描述了实现IPsec的系统的要求,这些系统的基本元素以及如何将这些元素结合起来…...
【数据结构/C++】线性表_双链表基本操作
#include <iostream> using namespace std; typedef int ElemType; // 3. 双链表 typedef struct DNode {ElemType data;struct DNode *prior, *next; } DNode, *DLinkList; // 初始化带头结点 bool InitDNodeList(DLinkList &L) {L (DNode *)malloc(sizeof(DNode))…...
前端已死?看看我的秋招上岸历程
背景 求职方向:web前端 技术栈:vue2、springboot(学校开过课,简单的学习过) 实习经历:两段,但都是实训类的,说白了就是类似培训,每次面试官问起时我也会坦诚交代&…...
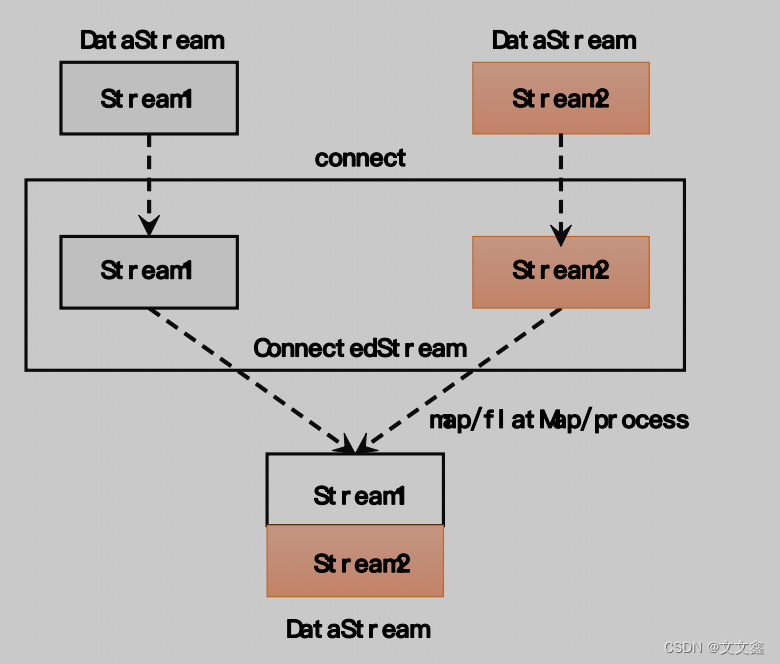
Flink Flink中的合流
一、Flink中的基本合流操作 在实际应用中,我们经常会遇到来源不同的多条流,需要将它们的数据进行联合处理。所以 Flink 中合流的操作会更加普遍,对应的 API 也更加丰富。 二、联合(Union) 最简单的合流操作…...

工业园区重金属废水深度处理工程项目,稳定出水0.1mg/l
随着环保要求不断提高,工业废水处理已成为众多企业的必修课。然而在工业生产中,如何有效处理含有重金属的废水成为了一个关键的挑战。 重金属废水是指含有汞、铅、铜、镉、锌、镍等有毒有害物质的废水,来源于矿山开采、金属冶炼、电镀、印刷线…...

element table滚动条失效
问题描述:给el-table限制高度之后滚动条没了 给看看咋设置的: <el-table:data"tableData"style"width: 100%;"ref"table"max-height"400"sort-change"changeSort">对比了老半天找不出问题,最后…...

代码随想录算法训练营 ---第四十六天
第一题: 简介: 本题的重点在于确定背包容量和物品数量 确定dp数组以及下标的含义 dp[i] : 字符串长度为i的话,dp[i]为true,表示可以拆分为一个或多个在字典中出现的单词。 2.确定递推公式 如果确定dp[j] 是true,且…...
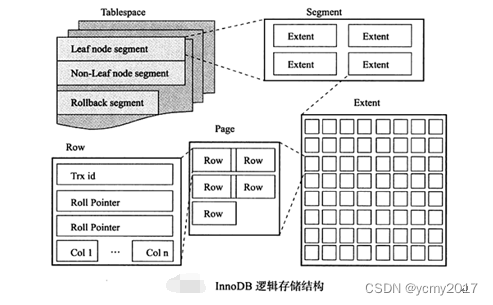
MySQL-02-InnoDB存储引擎
实际的业务系统开发中,使用MySQL数据库,我们使用最多的当然是支持事务并发的InnoDB存储引擎的这种表结构,下面我们介绍下InnoDB存储引擎相关的知识点。 1-Innodb体系架构 InnoDB存储引擎有多个内存块,可以认为这些内存块组成了一…...
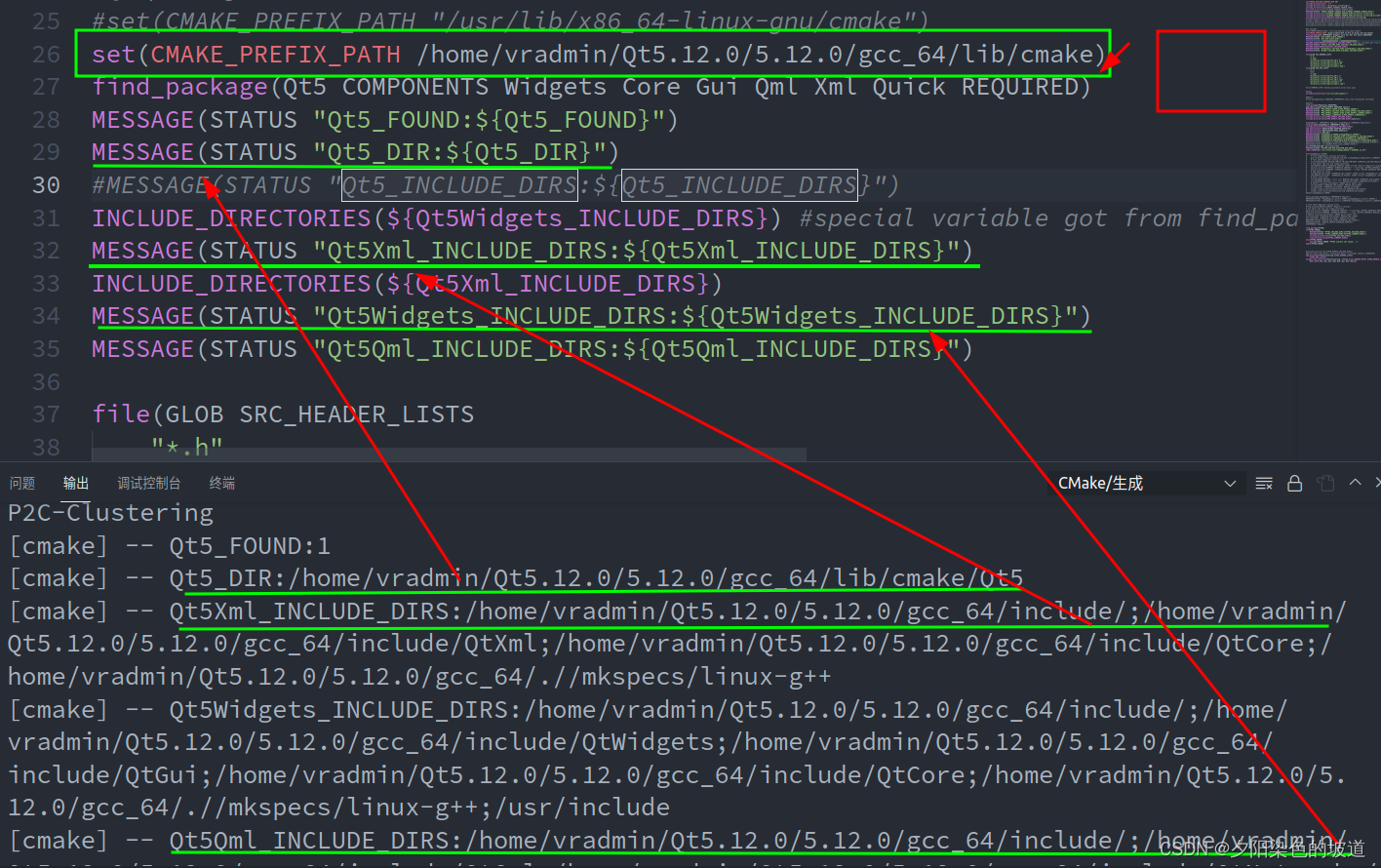
Qt路径和Anaconda中QT路径冲突(ubuntu系统)
最近做一个项目需要配置QT库,本项目配置环境如下: Qt version 5 Operating system, version and so on ubuntu 20.04 Description 之前使用过anaconda环境安装过QT5,所以在项目中CMakeLists文件中使用find_package时候,默认使用An…...

vue2.js添加水印
通过canvas生成水印图片 function addWaterMark(str) {let ctx document.createElement("canvas");ctx.width 900;ctx.height 450;ctx.style.display "none";let cans ctx.getContext("2d");cans.rotate((-20 * Math.PI) / 180);cans.font…...
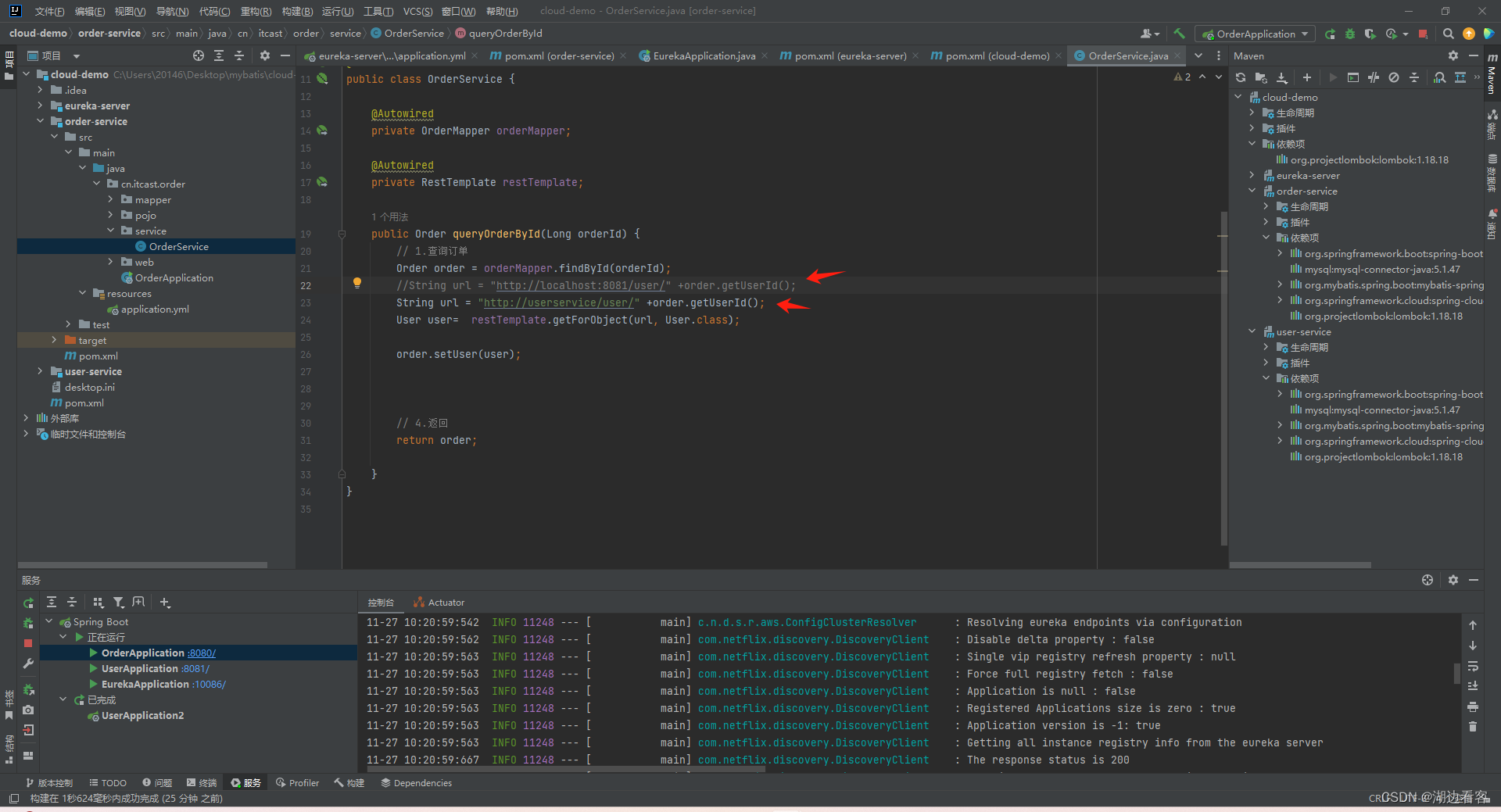
Eureka简单使用做微服务模块之间动态请求
创建一个eureka模块,引入eureka 为启动项加上EnableEurekaServer注解 配置信息 orderService和userService的操作是一样的 这里以orderService为例: 引入eureka客户端 加上 LoadBalanced注解 配置 orderService和userService都配置好了之后 启动 这样我们在http://localhos…...
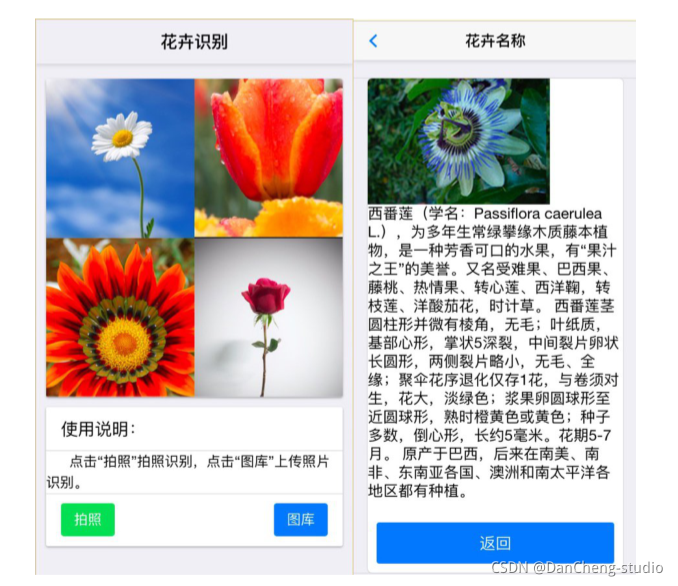
竞赛选题 题目:基于深度学习卷积神经网络的花卉识别 - 深度学习 机器视觉
文章目录 0 前言1 项目背景2 花卉识别的基本原理3 算法实现3.1 预处理3.2 特征提取和选择3.3 分类器设计和决策3.4 卷积神经网络基本原理 4 算法实现4.1 花卉图像数据4.2 模块组成 5 项目执行结果6 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 基…...

css-tricks网站图例
使用css实现钟表 <template><div><p><small>CSS sin() and cos() does <strong>NOT</strong> work in your browser.</small></p><div class"clock"><div id"app" class"clock-face"…...
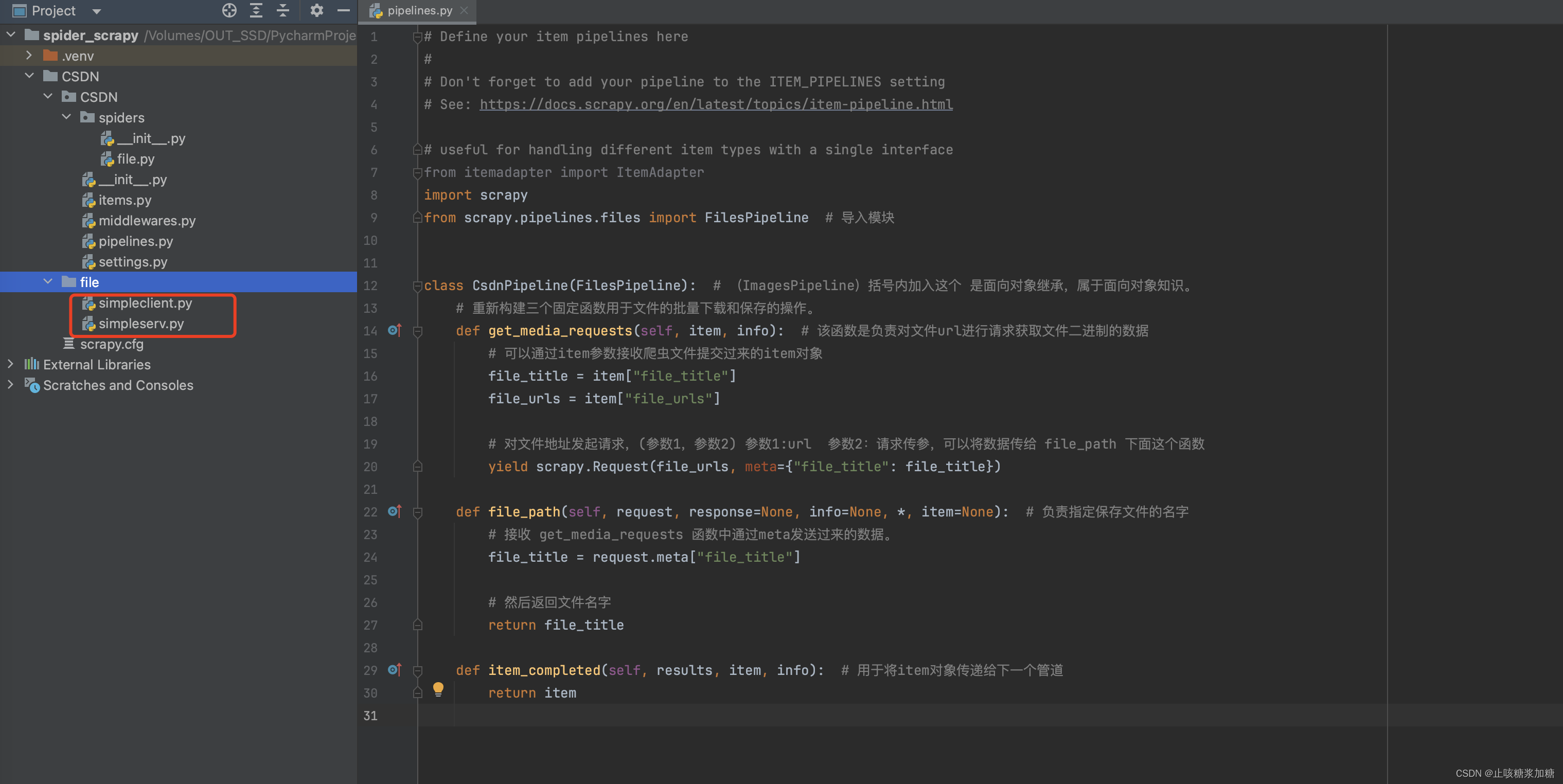
Scrapy框架内置管道之图片视频和文件(一篇文章齐全)
1、Scrapy框架初识(点击前往查阅) 2、Scrapy框架持久化存储(点击前往查阅) 3、Scrapy框架内置管道 4、Scrapy框架中间件(点击前往查阅) Scrapy 是一个开源的、基于Python的爬虫框架,它提供了…...

Linux文件与路径
Linux文件与路径 1、文件结构 Windows和Linux文件系统区别 在windows平台下,打开“此电脑”,我们可以看到盘符分区 每个驱动器都有自己的根目录结构,这样形成了多个树并列的情形 但是在 Linux 下,我们是看不到这些…...

【Qt】获取当前系统用户名:9种获取方式
目的 有时,在项目开发中,需要显示或者用到当前系统用户名信息。以下是几种获取系统用户名解决方案: 解决方案 1. 使用QDir::home() #include <QApplication> #include <QDir> #include <QDebug>int main(int argc, cha…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...
