排序算法:归并排序、快速排序、堆排序
归并排序
要将一个数组排序,可以先将它分成两半分别排序,然后再将结果合并(归并)起来。这里的分成的两半,每部分可以使用其他排序算法,也可以仍然使用归并排序(递归)。
我看《算法》这本书里对归并算法有两种实现,一种是“自顶向下”,另一种是“自底向上”。这两种方法,个人认为只是前者用了递归的方法,后者使用两个 for 循环模拟了递归压栈出栈的算法,本质上还是相同的(如果理解错误,还望大佬指出)。
算法步骤
1、将要排序的序列分成两部分。
2、将两部分分别各自排序。然后再将两个已经排序好的序列“归并”到一起,归并后的整个序列就是有序的。
3、将两个有序的序列归并的步骤:
3.1、先申请一个空间,大小足够容纳两个已经排序的序列。
3.2、设定两个指针,最初位置分别为两个已经排序序列的起始位置。
3.3、比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置。
3.4、重复3.3 步骤。
归并排序,比较重要的是“分治”思想和“归并”的操作。
归并操作,是将两个“有序”的序列,合并成一个有序的序列的方法。而这两个有序的序列,又是根据“分治”思想将一个学列分割成的两部分(将一个序列不断的分隔,到最后就剩一个的时候他自然就是有序的)。
public class MergeSort {public static void main(String[] args) {int[] nums = {12,123,432,23,1,3,6,3,-1,6,2,6};;sort(nums,0,nums.length -1);System.out.printf("finish!");}public static void sort(int[] nums,int left,int right){if(left >= right){return;}// 递归的将左半边排序sort(nums,left,right - left / 2 - 1); // 递归的将右半边排序sort(nums,right - left / 2 ,right);// 此时左右半边都分别各自有序,再将其归并到一起。// 如:[1,9,10 , 3,7,8]merge(nums,left,right - left / 2,right);}// 此方法叫做原地归并,将数组 nums 根据 mid 分隔开,左右看作是两个数组。// 类似于 merge(int[] nums1,int[] nums2),将 nums1 和 nums2 归并public static void merge(int[] nums ,int left,int mid,int right){int i = left,j = mid;int[] temp_nums = new int[nums.length];for(int key = left ; key <= right; key++)// 将原来数组复制到临时数组中。temp_nums[key] = nums[key];for(int key = i ; key <= right; key++){if(i > mid){nums[key] = temp_nums[j++];} else if (j > right) {nums[key] = temp_nums[i++];} else if (temp_nums[i] > temp_nums[j]) {nums[key] = temp_nums[j++];}else{nums[key] = temp_nums[i++];}}}}快速排序
快速排序是一种分治的排序算法,它将一个数组分成两个子数组,将两部分独立的排序
快速排序可能是应用最广泛的排序算法了。快速排序流行的原因是它实现简单、适用于各种不同的输入数据且在一般应用中比其他排序算法都要快得多。——《算法(第四版)》
算法步骤
- 从数列中挑出一个元素,称为 "基准"(pivot);
- 所有元素比"基准"值小的摆放在前面,所有元素比"基准"值大的摆在后面,相同的数可以到任一边。这个称为分区(partition)操作。
- 递归地(recursive)使用同样的方法把小于基准值元素的子数列和大于基准值元素的子数列排序;
算法过程
1、给定一个乱序的数组
[5,1,4,6,2,66,34,8]
2、选择第一个为基准数,此时把第一个位置置空。两个指针,left从左到右,找比 piovt “大”的数;right 从右向左,找比 piovt “小”的数。
left right| |
[_,1,4,6,2,66,34,8]|
piovt = 5
3、right 从右向左(<-),找比 piovt “小”的数 2。
left right| |
[_,1,4,6,2,66,34,8]|
piovt = 5
4、left从左到右(->),找到了比 piovt 大的数 6。
left right| |
[_,1,4,6,2,66,34,8]|
piovt = 5
5、此时将 left 和 right 上的数对调。
left right| |
[_,1,4,2,6,66,34,8]|
piovt = 5
6、right 继续向左查找,直到 left = right。(正常情况下要重复 4、5 步骤多次才会得到 left = right)
此时将 left 位置的数放到原来 piovt 位置上,将 piovt 放到 left 位置上。
leftright|
[2,1,4,5,6,66,34,8]- -|
piovt = 5
7、此时将整个数组根据 piovt 分割成两个部分,左边都比 piovt 小,右边都比 piovt 大。递归的处理左右两部分。
实现
public class QuickSort {public static void main(String[] args) {int[] nums = {5,1,4,6,2,66,34,8,34,534,5};int[] sorted = sort(nums,0 , nums.length - 1);System.out.println("finish!");}// 排序public static int[] sort(int[] nums , int left , int right){if(left <= right){ // 将 nums 以 mid 分成两部分// 左边的小于 nums[min]// 右边的大于 nums[min]int mid = partition(nums,left,right);// 递归sort(nums,left,mid - 1);sort(nums,mid + 1 ,right);}return nums;}public static int partition(int[] nums , int left , int right){//int pivot = left;int i = left , j = right + 1; // 左右两个指针int pivot = nums[left]; // 基准数,比他小的放到左边,比他大的放到右边。while ( true ){// 从右向左找比 pivot 小的。while (j > left && nums[--j] > pivot){if(j == left){// 到头了break;}}// 先从左向右找比 pivot 大的。while (i < right && nums[ ++ i] < pivot ){if( i == right){// 到头了break;}}if(i >= j ) break;// 交换 i 位置和 j 位置上的数// 因为此时 nums[i] > pivot 并且 nums[j] < pivotswap(nums,i , j);}// 由于 left 位置上的数是 pivot=// 此时 i = j 且 nums[i/j] 左边的数都小于 pivot , nums[i/j] 右边的数都大于 pivot。// 此时交换 left 和 j 位置上的数就是将 pivot 放到中间swap(nums,left,j);return j ;}// 交换数组中两个位置上的数public static void swap(int[] nums , int i1 , int i2){int n = nums[i1];nums[i1] = nums[i2];nums[i2] = n;}}堆排序
堆排序主要是利用“堆”这种数据结构的特性来进行排序,它本质上类似于“选择排序”。都是每次将最大值(或最小值),找出来放到数列尾部。不过“选择排序”需要遍历整个数列后选出最大值(可以到上面再熟悉下选择排序算法),“堆排序”是依靠堆这种数据结构来选出最大值。但是每次重新构建最大堆用时要比遍历整个数列要快得多。
堆排序中用到的两种堆,大顶堆和小顶堆:
1、大顶堆:每个节点的值都大于或等于其子节点的值(在堆排序算法中一般用于升序排列);
2、小顶堆:每个节点的值都小于或等于其子节点的值(在堆排序算法中一般用于降序排列);
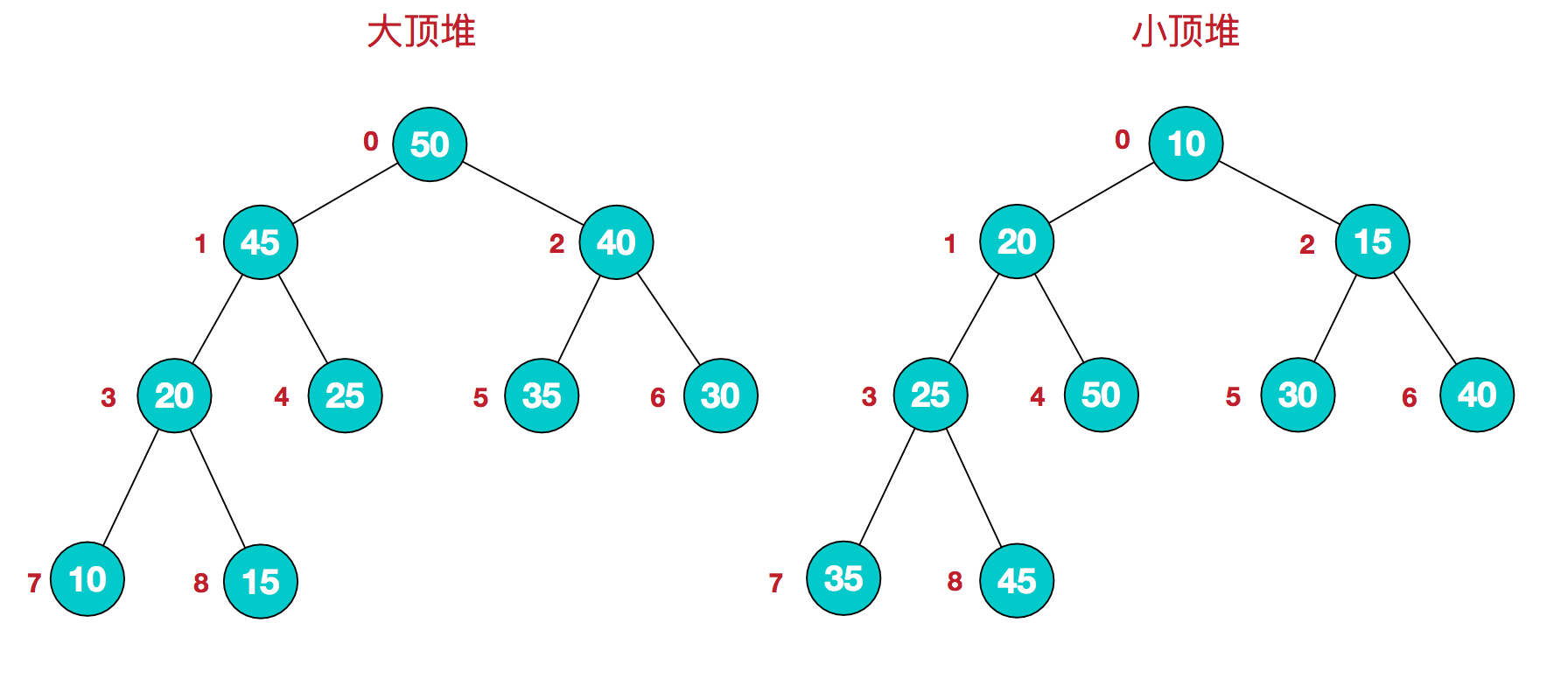
我们给树的每个节点编号,并将编号映射到数组的下标就是这样:

该数组从逻辑上是一个堆结构,我们用公式来描述一下堆的定义就是:
1、大顶堆:arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]
2、小顶堆:arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]
这里只要求父节点大于两个子节点,并没有要求左右两个子节点的大小关系。
算法过程
1、将一个 n 长的待排序序列arr = [0,……,n-1]构造成一个大顶堆。
2、此时数组的 0 位置(也就是堆顶),就是数组的最大值了,将其与数组的最后一个数交换。
3、将剩下 n-1 个数重复 1和2 操作,最终会得到一个有序的序列。
堆排序是“选择排序”的一种变体,算法中比较难的地方是用数组构建“大顶堆”或“小顶堆”的过程。
实现堆排序前,我们要知道怎么用数组构建一个逻辑上的最大堆,这里会用到几个公式(假设当前节点的序号是 i,可以结合上图理解下下面的公式):
1、左子节点的序号就是:2i + 1;
2、右子几点的序号就是:2i + 2;
3、父节点的序号就是:(i-1) / 2 (i不为0);
public class HeapSort {static int temp ;public static void main(String[] args) {int[] nums = {5,1,4,6,2,66,-1,34,-9,8};sort(nums);System.out.println("finish!");}public static void sort(int[] nums){// 第一步要先将 nums 构建成最大堆。for(int i = (nums.length - 1) / 2 ; i >= 0; i-- ){//从第一个非叶子结点从下至上,从右至左调整结构maxHeapify(nums,i,nums.length);}// 遍历数组// j 是需要排序的数组的最后一个索引位置。for(int j = nums.length - 1 ; j > 0 ; j --){// 每次都调整最大堆堆顶(nums[0]),与数组尾的数据位置(nums[j])。swap(nums,0,j);// 重新调整最大堆maxHeapify(nums,0,j);}}/*** 将 nums 从 i 开始的 len 长度调整成最大堆。* (注意:此方法只适合调整已经是最大堆但是被修改了的堆,或者只有三个节点的堆)* len :需要计算到数组 nums 的多长的地方。* i :父节点在的位置。*/public static void maxHeapify(int[] nums,int i , int len){// 是从左子节点开始int key = 2 * i + 1;if(key >= len){// 说明没有子节点。return;}// key + 1 是右子节点的位置。if(key + 1 < len && nums[key] < nums[key + 1]){// 此时说明右节点比左节点大。// 此时只要将父节点跟 右子节 点比就行了。key += 1;}if(nums[i] < nums[key]){// 子节点比父节点大,交换子父界节点的数据,将父节点设置为最大。swap(nums,i,key);// 此时子节点上的数变了,就要递归的再去,计算子节点是不是最大堆。maxHeapify(nums,key,len);}}/*** 交换 i 和 j 位置的数据*/public static void swap(int[] nums,int i,int j){temp = nums[i];nums[i] = nums[j];nums[j] = temp;}
}
相关文章:

排序算法:归并排序、快速排序、堆排序
归并排序 要将一个数组排序,可以先将它分成两半分别排序,然后再将结果合并(归并)起来。这里的分成的两半,每部分可以使用其他排序算法,也可以仍然使用归并排序(递归)。 我看《算法》…...
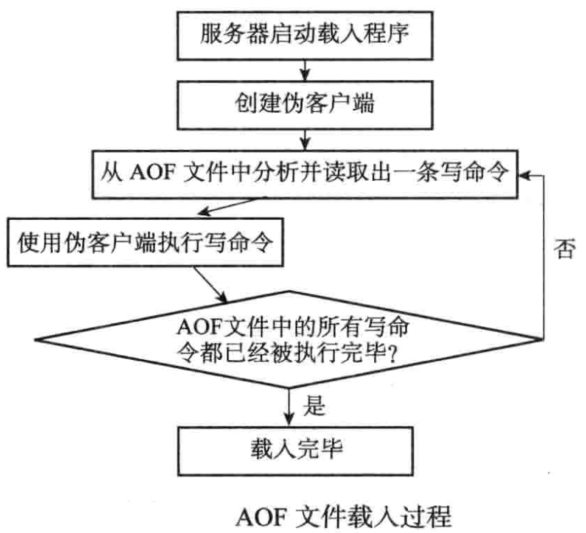
Redis 面试题——持久化
目录 1.概述1.1.Redis 的持久化功能是指什么?1.2.Redis 有哪些持久化机制? 2.RDB2.1.什么是 RDB 持久化?2.2.Redis 中使用什么命令来生成 RDB 快照文件?2.3.如何在 Redis 的配置文件中对 RDB 进行配置?2.4.✨RDB 持久化…...

Linux使用固定ip地址
设置静态ip,我们就需要修改 /etc/sysconfig/network-scripts/ifcfg-ens33 配置文件。 vim /etc/sysconfig/network-scripts/ifcfg-ens33 //进入网卡ens33的配置页面 (1) 将 BOOTPROTO dhcp 改成 BOOTPROTO static 也就是将动态ip,改成静态i…...
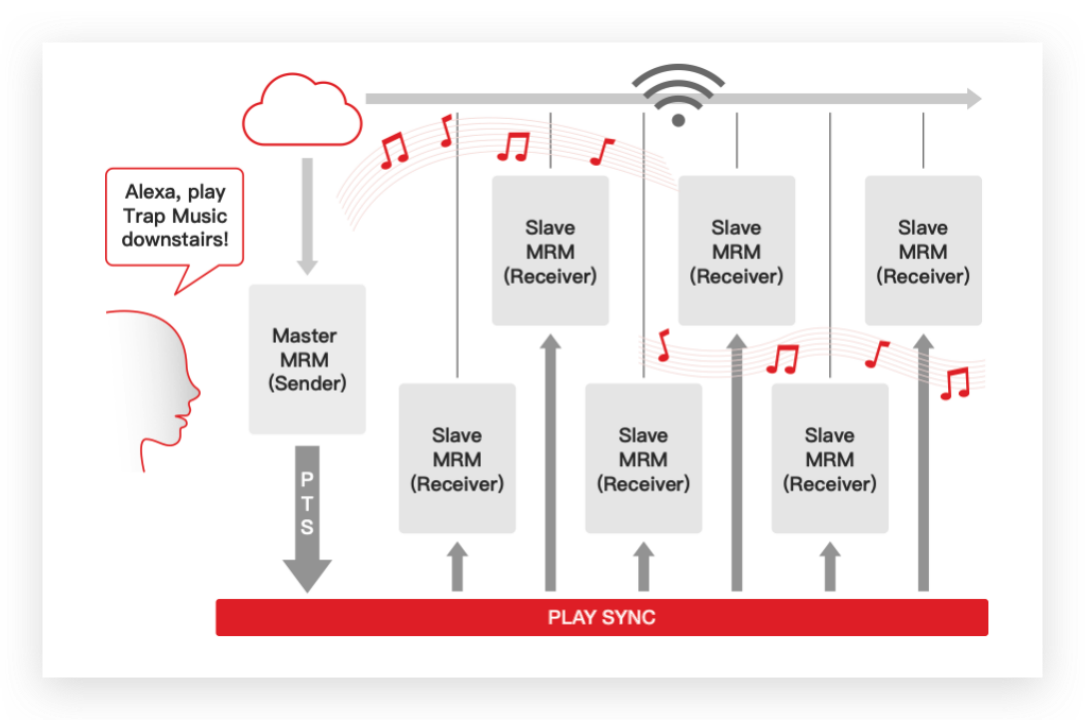
ESP Multi-Room Music 方案:支持音频实时同步播放 实现音乐互联共享
项目背景 随着无线通信技术的发展,针对不同音频应用领域的无线音频产品正不断涌现。近日,乐鑫科技推出了基于 Wi-Fi 的多扬声器互联共享音乐通信协议——ESP Multi-Room Music 方案。该方案使用乐鑫自研的基于 Wi-Fi 局域网的音频同步播放技术ÿ…...
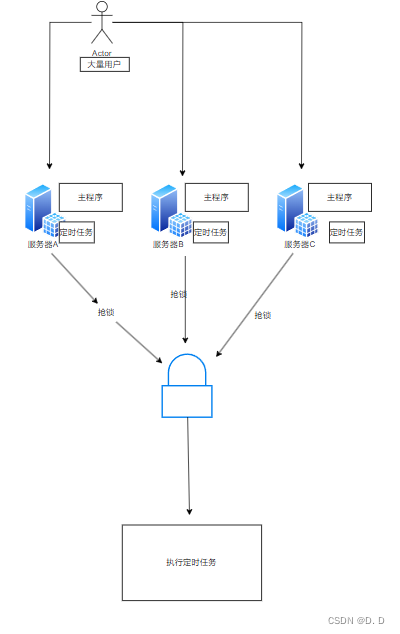
java分布式锁分布式锁
java分布式&锁&分布式锁 锁 锁的作用:有限资源的情况下,控制同一时间段,只有某些线程(用户/服务器)能访问到资源。 锁在java中的实现: synchronized关键字并发包的类 缺点:只对单个的…...
2. 流程控制|方法|数组|二维数组|递归
文章目录 流程控制代码块选择结构循环结构跳转控制关键字 方法方法的概述方法的重载Junit单元测试初识全限定类名 Debug 小技巧数组数组的基本概念数组的基本使用数组的声明数组的初始化 JVM内存模型什么是引用数据类型基本数据类型和引用数据类型的区别堆和栈中内容的区别 数组…...
?)
22. 自动装配有哪些限制(需要注意)?
自动装配有哪些限制(需要注意)? 一定要声明set方法覆盖: 你仍可以用 < constructor-arg >和 < property > 配置来定义依赖,这些配置将始终覆盖自动注入。基本数据类型:不能自动装配简单的属性,如基本数据…...
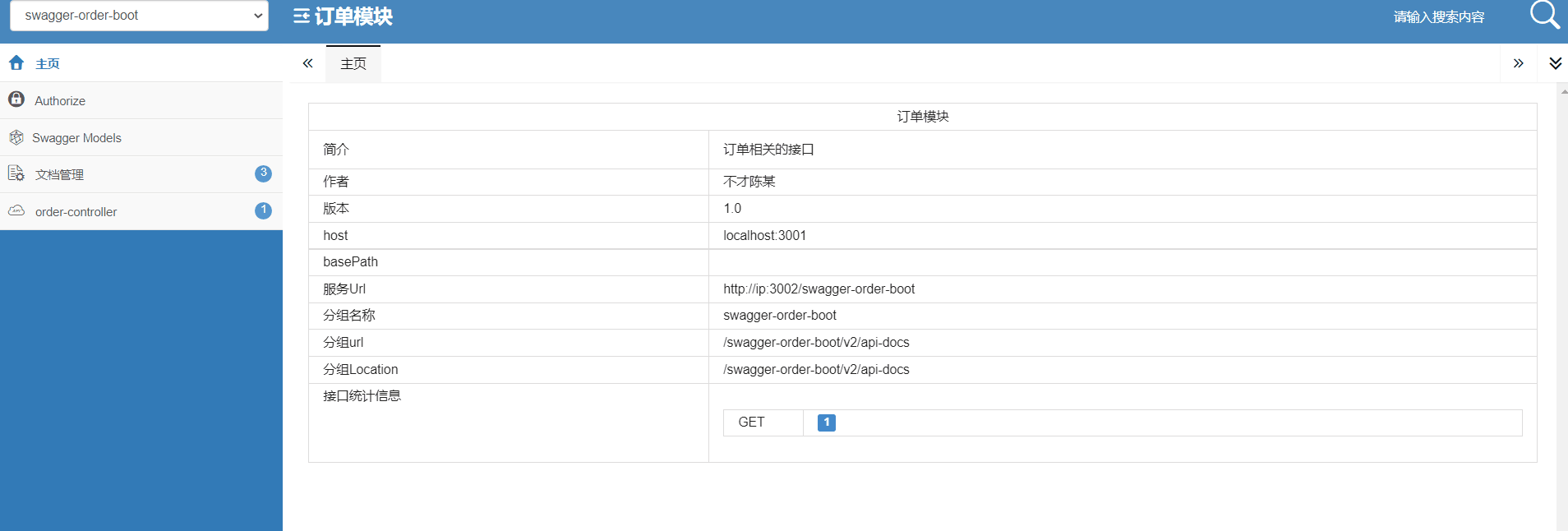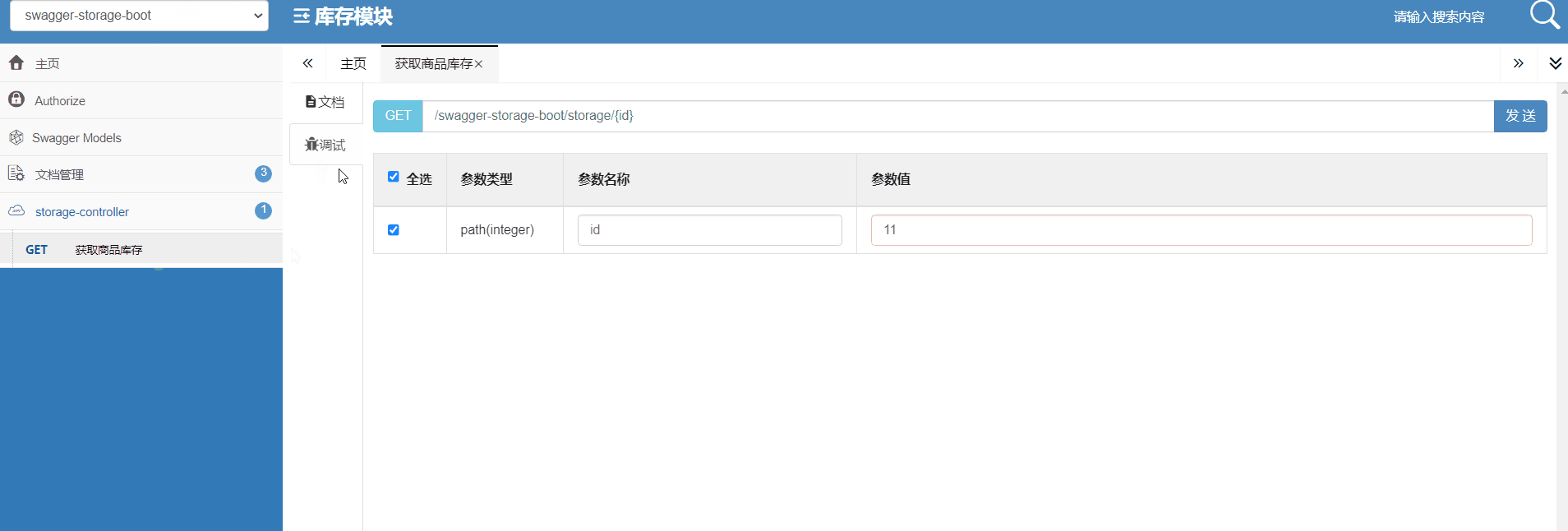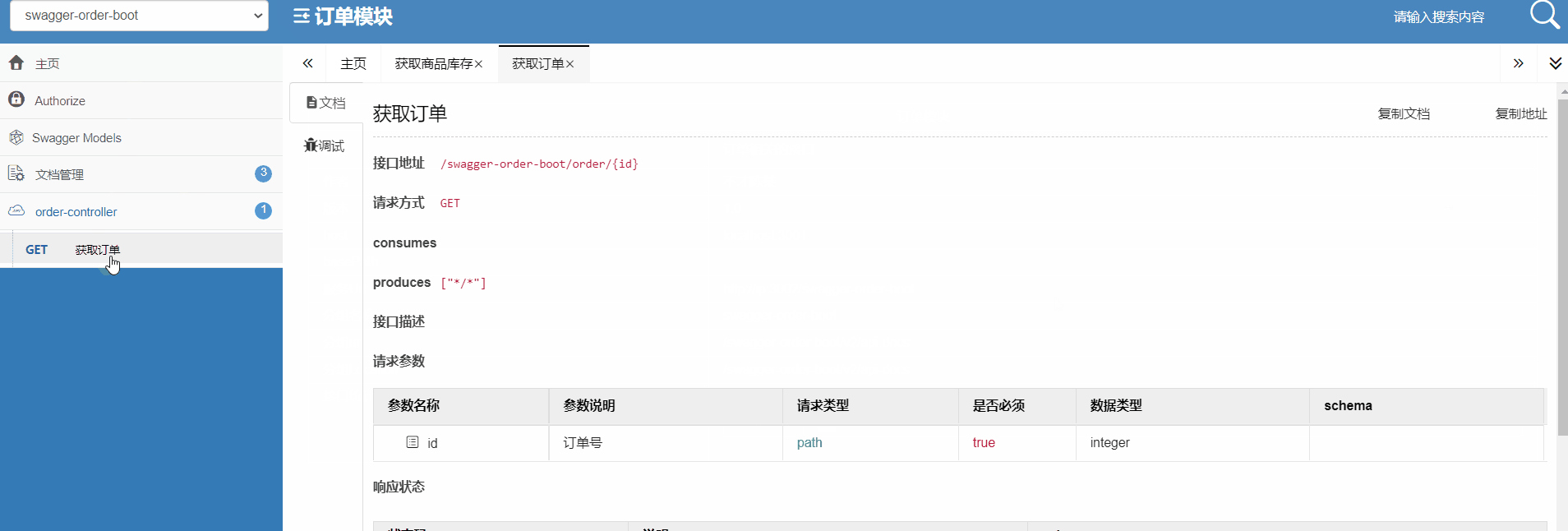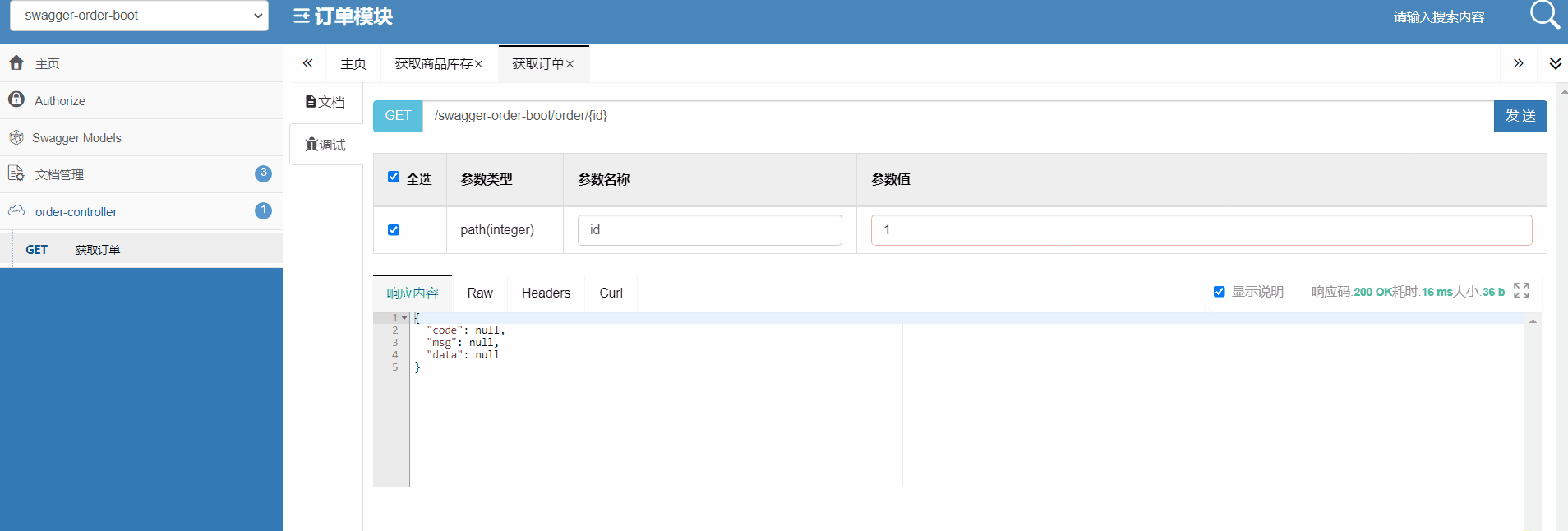
14 网关实战:网关聚合API文档
上节课介绍了网关层的认证鉴权,今天这节介绍一下网关层如何聚合API接口文文档。 为什么需要聚合API接口文档? 大型微服务系统模块众多,木谷博客系统就有9个,如果这些服务的接口地址没有一个统一,那么客户端将要保存每个服务的接口地址,这个肯定是不现实。 先来看一下A…...

css 固定按钮到页面顶部或者底部的实现方式
实现方式 要将按钮固定到顶部或底部,可以使用CSS的定位属性来实现。下面是一种常用的方法: 创建一个包含按钮的HTML元素,例如一个<div>元素。确保给它添加一个唯一的id,以便在CSS中进行定位。 <div id"myButton&qu…...
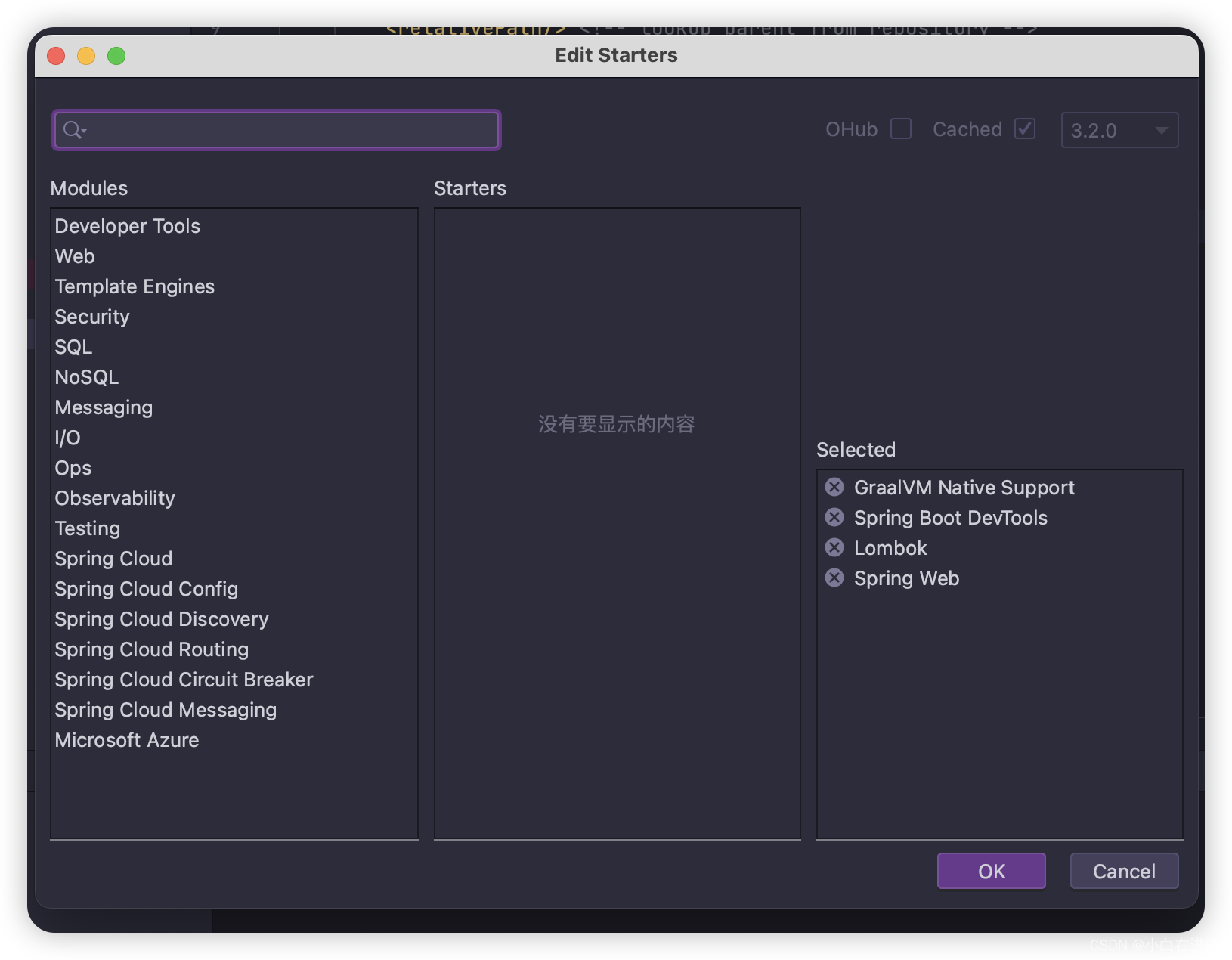
【Java Spring】SpringBoot常用插件
文章目录 1、Lombok1.1 IDEA社区版安装Lombok1.2 IDEA专业版安装Lombok1.3 Lombok的基本使用 2、EditStarters2.1 IDEA安装EditStarters2.2 EditStarters基本使用方法 1、Lombok 是简化Java开发的一个必要工具,lombok的原理是编译过程中将lombok的注解给去掉并翻译…...

GPT还远远不是真正的智能
GPT是一个基于深度学习的自然语言处理模型,它可以生成逼真的文本。虽然GPT在生成文本方面取得了显著的进展,但它并不具备真正的智能。GPT是通过训练模型来学习语言模式,它不具备理解、推理、判断和主动学习的能力。它只是根据已有的语料库生成…...

计算机网络:网络层
0 本节主要内容 问题描述 解决思路 1 问题描述 两大问题(重点,也是难点): 地址管理;路由选择。 1.1 子问题1:地址管理 网络上的这些主机和节点都需要使用一种规则来区分,就相当于是一种身…...

消息队列进阶-1.消息队列的应用场景与选型
👏作者简介:大家好,我是爱吃芝士的土豆倪,24届校招生Java选手,很高兴认识大家📕系列专栏:Spring源码、JUC源码、Kafka原理🔥如果感觉博主的文章还不错的话,请ὄ…...

浅谈堆和栈内存以及编程语言
浅谈堆和栈内存以及编程语言 栈和堆C 和 C# 的区别:C#总结 编程语言C汇编语言(Assembly Language):机器语言(Machine Language): 拓展C#依赖注入(Dependency Injection)模…...

SpringBootWeb案例_01
Web后端开发_04 SpringBootWeb案例_01 原型展示 成品展示 准备工作 需求&环境搭建 需求说明: 完成tlias智能学习辅助系统的部门管理,员工管理 环境搭建 准备数据库表(dept、emp)创建springboot工程,引入对应…...

C语言数据结构-----栈和队列练习题(分析+代码)
前言 前面的博客写了如何实现栈和队列,下来我们来看一下队列和栈的相关习题。 链接: 栈和队列的实现 文章目录 前言1.用栈实现括号匹配2.用队列实现栈3.用栈实现队列4.设计循环队列 1.用栈实现括号匹配 此题最重要的就是数量匹配和顺序匹配。 用栈可以完美的做到…...
uniapp基础-教程之HBuilderX配置篇-01
uniapp教程之HBuilderX配置篇-01 为什么要做这个教程的梳理,主要用于自己学习和总结,利于增加自己的积累和记忆。首先下载HBuilderX,并保证你的软件在C盘进行运行,最好使用英文或者拼音,这个操作是为了保证软件的稳定…...
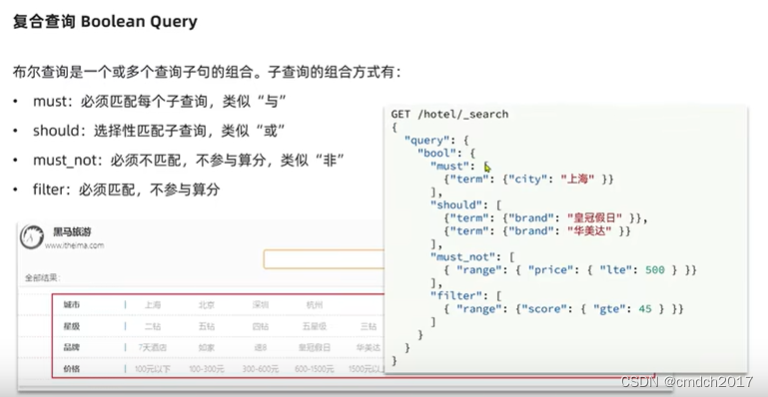
【备忘录】快速回忆ElasticSearch的CRUD
导引——第一条ElasticSearch语句 测试分词器 POST /_analyze {"text":"黑马程序员学习java太棒了","analyzer": "ik_smart" }概念 语法规则 HTTP_METHOD /index/_action/IDHTTP_METHOD 是 HTTP 请求的方法,常见的包括…...

影响PPC广告成本预算的因素,如何计算亚马逊PPC广告预算——站斧浏览器
亚马逊PPC,又称按点击付费(Pay Per Click),是一种只有用户点击你的广告时才会向你收费的模式。那么影响PPC广告成本预算的因素,如何计算亚马逊PPC广告预算? 影响PPC广告成本预算的因素 1、产品类别:不同类别的产品竞争程度不同&…...

Qt 信号和槽
目录 概念 代码 mainwindow.h me.h xiaohuang.h main.cc mainwindow.cc me.cc xianghuang.cc mainwindow.ui 自定义信号的要求和注意事项: 自定义槽的要求和注意事项: 概念 信号槽是 Qt 框架引以为豪的机制之一。所谓信号槽,实际就是观察者模式(发布-订…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...
