acwing算法基础之动态规划--线性DP和区间DP
目录
- 1 基础知识
- 2 模板
- 3 工程化
1 基础知识
线性DP:状态转移表达式存在明显的线性关系。
区间DP:与顺序有关,状态与区间有关。
2 模板
3 工程化
题目1:数字三角形。
解题思路:直接DP即可,f[i][j]可以来自f[i-1][j] + a[i][j]和f[i-1][j-1] + a[i][j],注意f[i-1][j]不存在的情况(最后一个点)和f[i-1][j-1]不存在的情况(第一个点)。
C++代码如下,
#include <iostream>using namespace std;const int N = 510;
int n;
int a[N][N];
int f[N][N];int main() {cin >> n;for (int i = 0; i < n; ++i) {for (int j = 0; j < i + 1; ++j) {cin >> a[i][j];}}for (int i = 0; i < N; ++i) {for (int j = 0; j < N; ++j) {f[i][j] = -0x3f3f3f3f;}}f[0][0] = a[0][0];for (int i = 1; i < n; ++i) {for (int j = 0; j < i + 1; ++j) {f[i][j] = max(f[i][j], f[i-1][j] + a[i][j]);if (j - 1 >= 0) f[i][j] = max(f[i][j], f[i-1][j-1] + a[i][j]);}}int res = -0x3f3f3f3f;for (int j = 0; j < n; ++j) res = max(res, f[n-1][j]);cout << res << endl;return 0;
}
题目2:最长上升子序列。注意可以连续,比如3 1 2 1 8 5 6,那么它的最长上升子序列为1 2 5 6,长度为4。
解题思路:DP即可。
状态定义,f[i]表示以第 i i i元素结尾的上升子序列的最大长度。
状态转移,有,
- 没有上一个元素,即
f[i] = 1。 - 从第 i − 1 i-1 i−1个元素转移过来,需要满足
a[i-1] < a[i],则f[i-1] + 1。 - 从第 i − 2 i-2 i−2个元素转移过来,需要满足
a[i-2] < a[i],则f[i-2] + 1。
…… - 从第 0 0 0个元素转移过来,需要满足
a[0] < a[i],则f[0] + 1。
C++代码如下,
#include <iostream>using namespace std;const int N = 1010;
int n;
int a[N];
int f[N];int main() {cin >> n;for (int i = 0; i < n; ++i) cin >> a[i];for (int i = 0; i < n; ++i) {f[i] = 1;for (int j = 0; j < i; ++j) {if (a[j] < a[i]) f[i] = max(f[i], f[j] + 1);} }int res = 0;for (int i = 0; i < n; ++i) res = max(res, f[i]);cout << res << endl;return 0;
}
同时输出最长上升子序列,那么此时只需要记住当前状态是从哪一个状态转移过来的,然后逆序输出即可。C++代码如下,
#include <iostream>
#include <algorithm>using namespace std;const int N = 1010;
int n;
int a[N];
int f[N];
int g[N];int main() {cin >> n;for (int i = 0; i < n; ++i) cin >> a[i];for (int i = 0; i < n; ++i) {f[i] = 1;g[i] = -1; //g[i]=-1表示它是子序列的起点for (int j = 0; j < i; ++j) {if (a[j] < a[i]) {if (f[i] < f[j] + 1) {f[i] = f[j] + 1;g[i] = j;//g[i]=j表示状态f[i]是从状态f[j]转移过来的}}} }int res = 0;for (int i = 0; i < n; ++i) {if (f[i] > f[res]) {res = i;}}cout << f[res] << endl;//输出最长子序列的长度vector<int> ans; //最长子序列for (int i = res; i != -1; i = g[i]) {ans.emplace_back(a[i]);}reverse(ans.begin(), ans.end());for (int i = 0; i < ans.size(); ++i) cout << ans[i] << " ";cout << endl;return 0;
}
测试样例,
输入:
7
3 1 2 1 8 5 6
输出:
4
1 2 5 6
题目3:最长公共子序列,给定字符串a和字符串b,求它们的最长公共子序列。例如acbd和abedc,则它们的最长公共子序列为abd,长度为3。
思路:利用DP来求解,由于这里求的是最大长度,因此在状态转移时,可以适当放大,以便可以表示相应转移路径。
状态定义,f[i][j]:从字符串a前i个中选且从字符串b中前j个中选的公共子序列的最大长度。
状态转移,有,
- a[i]不在最优公共子序列当中,b[j]不在最优公共子序列当中,则
f[i-1][j-1]。 - a[i]在最优公共子序列当中,b[j]不在最优公共子序列当中,无法表示???,故将其放大,为
f[i][j-1]。 - a[i]不在最优公共子序列当中,b[j]在最优公共子序列当中,无法表示???,故将其放大,为
f[i-1][j]。 - a[i]在最优公共子序列当中,b[j]在最优公共子序列当中,要求
a[i]=b[j],则f[i-1][j-1] + 1。
进一步思考,由于进行了放大,因此第(2)种情况和第(3)种情况包含了第(1)种情况。因此在代码实现时,可以考虑如下状态转移f[i][j-1]、f[i-1][j]和f[i-1][j-1] + 1。
C++代码如下,
#include <iostream>using namespace std;const int N = 1010;
char a[N], b[N];
int n, m;
int f[N][N];int main() {cin >> n >> m;cin >> a + 1 >> b + 1;for (int i = 1; i <= n; ++i) {for (int j = 1; j <= m; ++j) {f[i][j] = max(f[i-1][j], f[i][j-1]);if (a[i] == b[j]) f[i][j] = max(f[i][j], f[i-1][j-1] + 1);}}cout << f[n][m] << endl;return 0;
}
题目4:合并相邻石子的最小代价。例如1 3 5 2,合并前两堆石子1和3的代价是4,得到4 5 2。
解题思路:区间合并类DP,状态定义围绕着区间,然后怎么层层递进计算状态,比较考验。答案是枚举区间长度来计算。
状态定义,f[i][j]:合并第i~j堆石子的最小代价。
状态转移,有,
- 最后一次合并为[i,i]和[i+1,j]这两个区间合并,即
f[i][i] + f[i + 1][j] + s[j] - s[i - 1],其中s[i]表示前缀和。 - 最后一次合并为[i,i+1]和[i+2,j]这两个区间合并,即
f[i][i + 1] + f[i + 2][j] + s[j] - s[i - 1]。 - 最后一次合并为[i,i+2]和[i+3,j]这两个区间合并,即
f[i][i + 2] + f[i + 3][j] + s[j] - s[i - 1]。
…… - 最后一次合并为[i,j-1]和[j,j]这两个区间合并,即
f[i][j - 1] + f[j][j] + s[j] - s[i - 1]。
初始化,f[i][i]=0,然后其余初始化为正无穷大,比如1e9。
最终答案为,f[1][n]。
注意状态的遍历,是通过区间长度从1到n实现的。
C++代码如下,
#include <iostream>using namespace std;const int N = 310;
int a[N];
int s[N];
int f[N][N];
int n;int main() {cin >> n;for (int i = 1; i <= n; ++i) cin >> a[i];for (int i = 1; i <= n; ++i) s[i] += s[i-1] + a[i];for (int len = 2; len <= n; ++len) {//枚举左端点for (int i = 0; i + len - 1 <= n; ++i) {int l = i, r = i + len - 1;f[l][r] = 1e9;for (int k = l; k < r; ++k) {f[l][r] = min(f[l][r], f[l][k] + f[k+1][r] + s[r] - s[l-1]);}}}cout << f[1][n] << endl;return 0;
}
相关文章:

acwing算法基础之动态规划--线性DP和区间DP
目录 1 基础知识2 模板3 工程化 1 基础知识 线性DP:状态转移表达式存在明显的线性关系。 区间DP:与顺序有关,状态与区间有关。 2 模板 3 工程化 题目1:数字三角形。 解题思路:直接DP即可,f[i][j]可以来…...
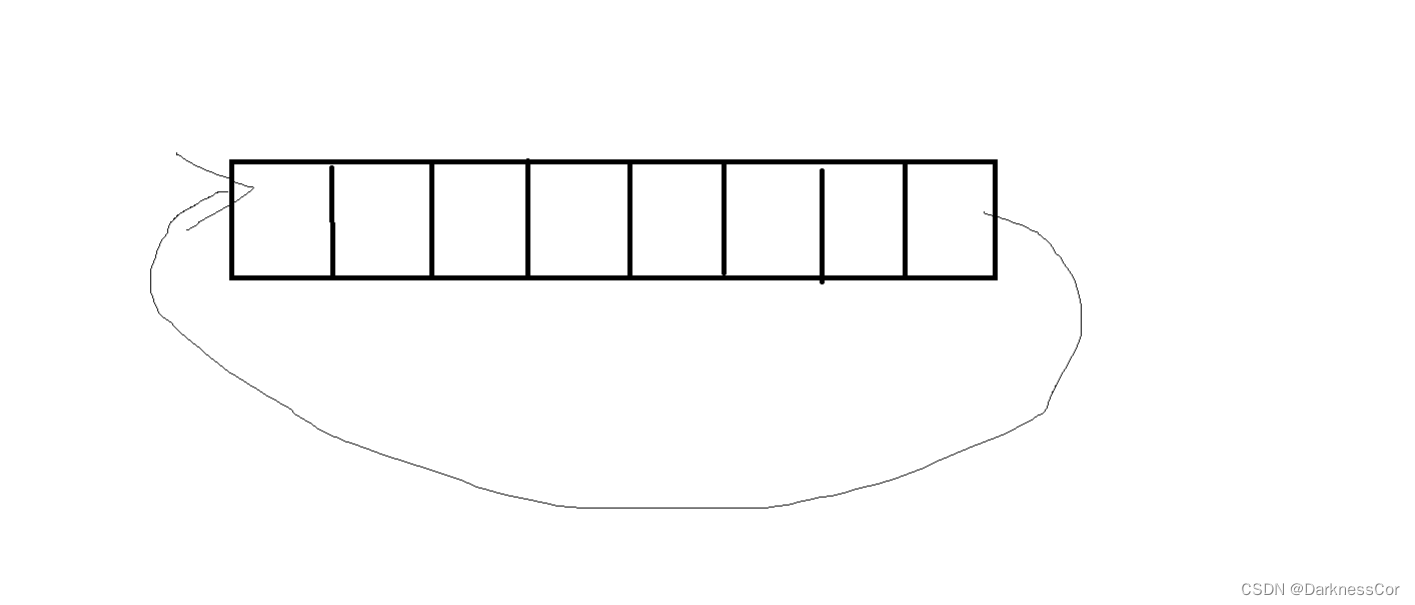
力扣 622.设计循环队列
目录 1.解题思路2.代码实现 1.解题思路 首先,该题是设计循环队列,因此我们有两种实现方法,即数组和链表,但具体考虑后,发现数组实现要更容易一些,因此使用数组实现,因此我们要给出头和尾变量&a…...

初识Linux(2).妈妈再也不用担心我Linux找不到门了。
文章目录 前言 1.man指令(重要):例如: 2.cp指令(重要):例如:把123.txt复制到a目录中类似window如下操作: 3.mv例如:类似window如下操作: 4.nano例…...

房屋租赁出售经纪人入驻小程序平台
一款专为房屋中介开发的小程序平台,支持独立部署,源码交付,数据安全无忧。 核心功能:房屋出租、经纪人独立后台、分佣后台、楼盘展示、房型展示、在线咨询、地址位置配套设施展示。 程序已被很多房屋交易中介体验使用过&#x…...
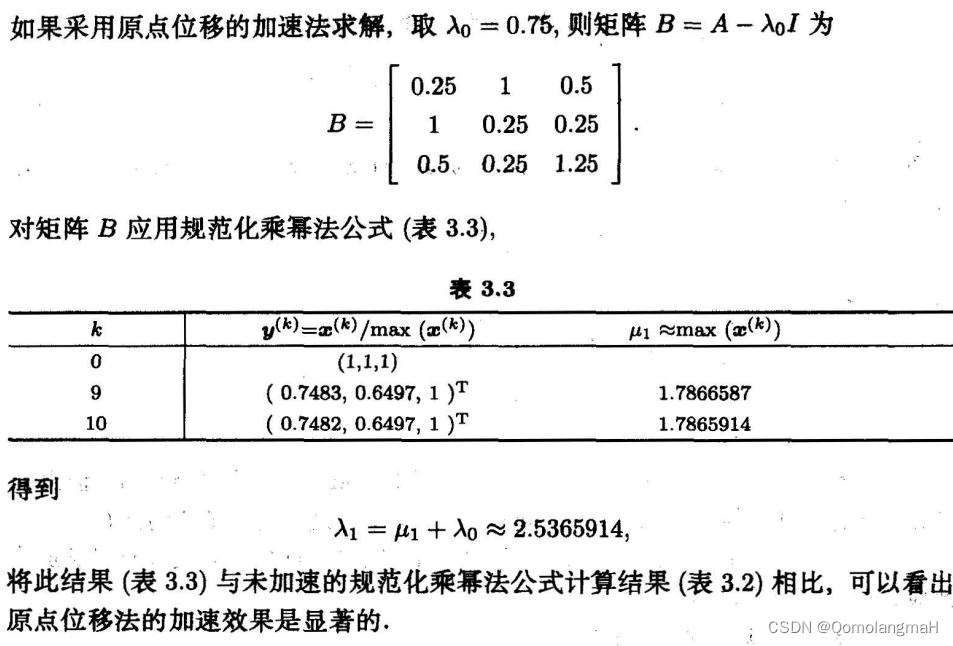
【计算方法与科学建模】矩阵特征值与特征向量的计算(五):乘幂法的加速(带有原点移位的乘幂法)
文章目录 一、Jacobi 旋转法二、Jacobi 过关法三、Householder 方法四、乘幂法四、乘幂法的加速 矩阵的特征值(eigenvalue)和特征向量(eigenvector)在很多应用中都具有重要的数学和物理意义。 本文将详细介绍乘幂法的基本原理和步…...

2023年【起重机械指挥】考试题库及起重机械指挥考试资料
题库来源:安全生产模拟考试一点通公众号小程序 2023年【起重机械指挥】考试题库及起重机械指挥考试资料,包含起重机械指挥考试题库答案和解析及起重机械指挥考试资料练习。安全生产模拟考试一点通结合国家起重机械指挥考试最新大纲及起重机械指挥考试真…...
)
GoLang语言范围(Range)
目录 一、在数组、切片上使用‘range’ 二、在映射上使用range 三、在通道上使用range Go语言中的range关键字用于迭代数组(数组、切片、字符串)、映射(map)、通道(channel)或者在 for 循环中迭代每一个…...

汽车电子 -- 车载ADAS之FCW(前方碰撞预警)
相关法规文件: FCW: GB∕T 33577-2017 智能运输系统 车辆前向碰撞预警系统 性能要求和测试规程 一、前方碰撞预警 FCW( Forward Collision Warning) 参看:法规标准-GB/T 33577标准解读(2017版) 1、状态机 系统关闭 当车辆前向碰撞预警系…...

爬虫系统Docker和Kubernetes部署运维最佳实践
在构建和管理爬虫系统时,使用Docker和Kubernetes可以带来诸多好处,如方便的部署、弹性伸缩和高可靠性。然而,正确的部署和运维实践对于确保系统稳定运行至关重要。在本文中,我将分享爬虫系统在Docker和Kubernetes上的最佳部署和运…...

音视频5、libavformat-1
libavformat库,是FFmpeg中用于处理各种媒体容器格式(media container format)的库。它的两个最主要的功能是 : demuxing:解封装,将一个媒体文件分割为多个多媒体流 muxing:封装,将多个多媒体数据流写入到指定媒体容器格式的文件中 这两个过程所做的…...

【数据结构复习之路】树和二叉树(严蔚敏版)万字详解主打基础
专栏:数据结构复习之路 复习完上面四章【线性表】【栈和队列】【串】【数组和广义表】,我们接着复习 树和二叉树,这篇文章我写的非常详细且通俗易懂,看完保证会带给你不一样的收获。如果对你有帮助,看在我这么辛苦整理…...

nginx使用详解:转发规则、负载均衡、server_name
文章目录 一、nginx常用的转发规则location 指令说明location转发使用 二、upstream负载均衡使用三、server_name使用四、其他常用配置限制请求类型处理静态资源目录遍历问题限制客户端使用的ip或者域名 五、需要注意的地方location /api1 探讨location ~ /api1 探讨࿰…...
HarmonyOS 数据持久化 Preferences 如何在页面中对数据进行读写
背景介绍 最近在了解并跟着官方文档尝试做一个鸿蒙app 小demo的过程中对在app中保存数据遇到些问题 特此记录下来 这里的数据持久化以 Preferences为例子展开 废话不多说 这里直接上节目(官方提供的文档示例:) 以Stage模型为例 1.明确preferences的类型 import data_prefer…...

ESP32-Web-Server编程- JS 基础 4
ESP32-Web-Server编程- JS 基础 4 概述 HTML 内联事件处理器,你永远不应该使用 HTML 事件处理器属性——因为那些已经过时了,使用它们是不好的做法。 在前端编程中,除了将期望发生的事件写为 JS 文件外,还可以使用一些组件自带…...

JAVA的反射机制
什么是反射机制 Java反射机制是指在运行时动态地获取类的信息并操作类的成员(属性、方法、构造方法等)的能力。通过反射,我们可以解析出类的完整信息,包括构造函数、成员变量、继承关系等。以下是一个使用反射机制创建对象、调用…...
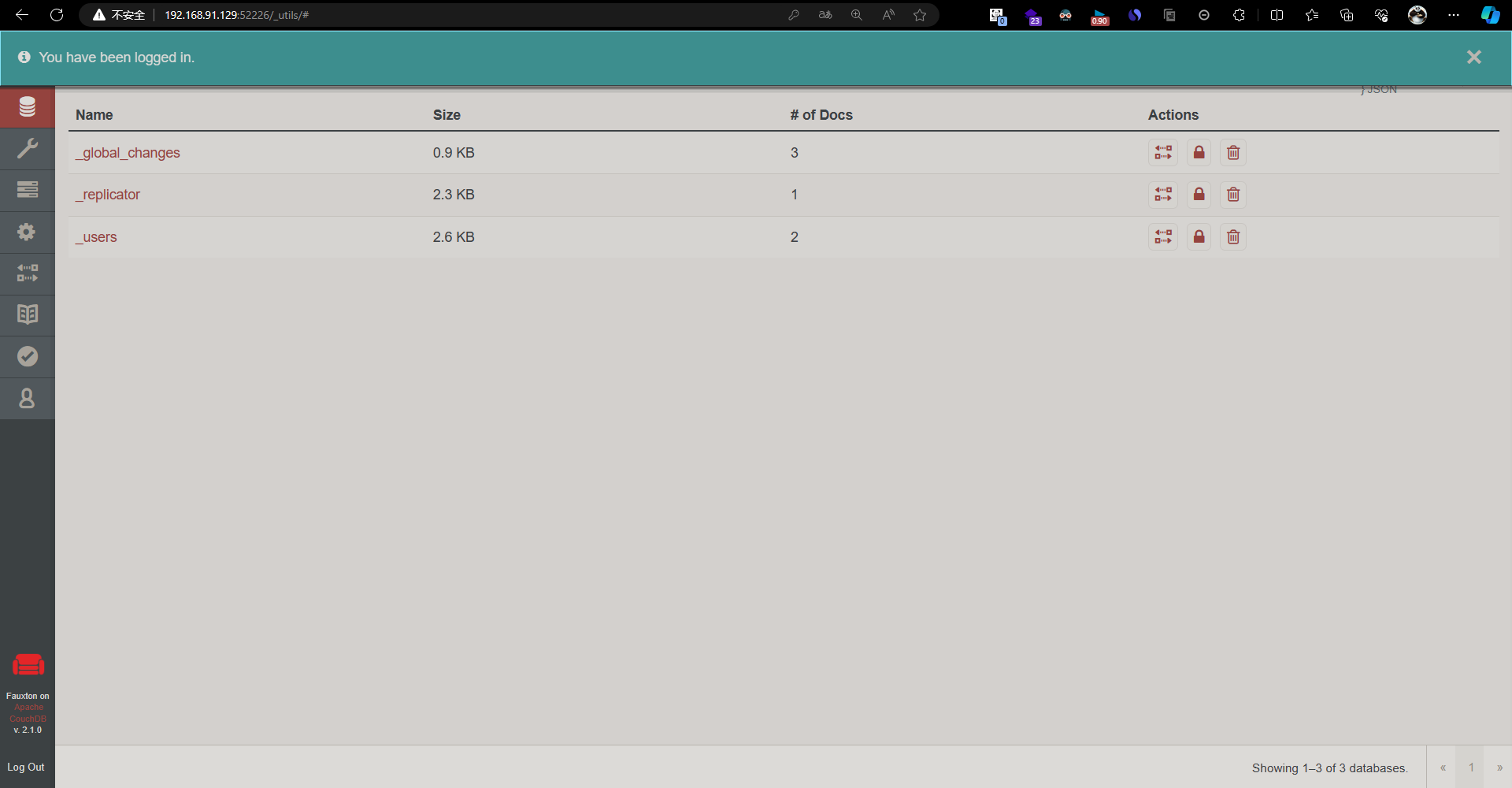
Couchdb 权限绕过漏洞复现(CVE-2017-12635)
Couchdb 权限绕过漏洞复现(CVE-2017-12635) 开启环境给了三个端口号,不知道哪个是正常的,最后试出来52226端口正常。 登录URL:http://192.168.91.129:52226/_utils/# 来到了登录页面 用postman发送PUT…...

GZ031 应用软件系统开发赛题第2套
2023年全国职业院校技能大赛 应用软件系统开发赛项(高职组) 赛题第2套 工位号: 2023年4月 竞赛说明 一、项目背景 党的二十大报告指出,要加快建设制造强国、数字中国,推动制造业高端化、智能化、…...
lack——主页前后端开发优化(精华:java多线程实现数据插入)
lack——主页前后端开发优化 前端开发主页 最容易的方式:list列表<template><van-cardv-for"user in props.userList":desc"user.profile":title"${user.username} (${user.planetCode})":thumb"user.avatarUrl"…...

Anaconda深度学习环境配置命令参考
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 Anaconda深度学习环境配置 Anaconda 管理1. 检查 Anaconda 版本2. 获取版本号3. 列出所有的虚拟环境4. 查看环境管理的全部命令帮助5. conda升级6. conda升级后释放空间 Anac…...
【iOS】知乎日报
文章目录 前言一、首页1.网络的异步请求2.避免同一网络请求执行多次3.下拉刷新与上拉加载的实现下拉刷新上拉加载 二、网页1.webView的实现2.webView的滑动加载3.网页与首页内容的同步更新 三、评论区Masonory实现行高自适应 四、收藏中心通过FMDB实现数据持久化1.创建或打开数…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...
