【LeetCode:1457. 二叉树中的伪回文路径 | 二叉树 + DFS +回文数】

| 🚀 算法题 🚀 |
🌲 算法刷题专栏 | 面试必备算法 | 面试高频算法 🍀
🌲 越难的东西,越要努力坚持,因为它具有很高的价值,算法就是这样✨
🌲 作者简介:硕风和炜,CSDN-Java领域新星创作者🏆,保研|国家奖学金|高中学习JAVA|大学完善JAVA开发技术栈|面试刷题|面经八股文|经验分享|好用的网站工具分享💎💎💎
🌲 恭喜你发现一枚宝藏博主,赶快收入囊中吧🌻
🌲 人生如棋,我愿为卒,行动虽慢,可谁曾见我后退一步?🎯🎯
| 🚀 算法题 🚀 |


🍔 目录
- 🚩 题目链接
- ⛲ 题目描述
- 🌟 求解思路&实现代码&运行结果
- ⚡ 二叉树 + DFS
- 🥦 求解思路
- 🥦 实现代码
- 🥦 运行结果
- 💬 共勉
🚩 题目链接
- 1457. 二叉树中的伪回文路径
⛲ 题目描述
给你一棵二叉树,每个节点的值为 1 到 9 。我们称二叉树中的一条路径是 「伪回文」的,当它满足:路径经过的所有节点值的排列中,存在一个回文序列。
请你返回从根到叶子节点的所有路径中 伪回文 路径的数目。
示例 1:
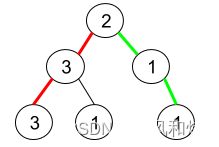
输入:root = [2,3,1,3,1,null,1]
输出:2
解释:上图为给定的二叉树。总共有 3 条从根到叶子的路径:红色路径 [2,3,3] ,绿色路径 [2,1,1] 和路径 [2,3,1] 。
在这些路径中,只有红色和绿色的路径是伪回文路径,因为红色路径 [2,3,3] 存在回文排列 [3,2,3] ,绿色路径 [2,1,1] 存在回文排列 [1,2,1] 。
示例 2:
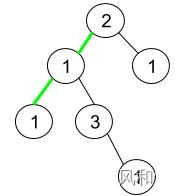
输入:root = [2,1,1,1,3,null,null,null,null,null,1]
输出:1
解释:上图为给定二叉树。总共有 3 条从根到叶子的路径:绿色路径 [2,1,1] ,路径 [2,1,3,1] 和路径 [2,1] 。
这些路径中只有绿色路径是伪回文路径,因为 [2,1,1] 存在回文排列 [1,2,1] 。
示例 3:
输入:root = [9]
输出:1
提示:
给定二叉树的节点数目在范围 [1, 105] 内
1 <= Node.val <= 9
🌟 求解思路&实现代码&运行结果
⚡ 二叉树 + DFS
🥦 求解思路
- 考察点1:树的深度优先遍历,找到从根节点到叶子节点的所有节点。
- 考察点2:怎么判断一条路径中的节点是否是一个回文路径呢?计数,如果一个路径中某一个数字出现的次数是偶数,那么忽略,如果是奇数,至少容忍一次,多于一次,不可以构成回文路径。
- 考察点3:什么是回文序列,就是正着读,和反着读都一样,构成回文序列。
- 具体实现代码如下:
🥦 实现代码
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public int pseudoPalindromicPaths (TreeNode root) {int[] cnt=new int[10];return process(root,cnt);}public int process(TreeNode root,int[] cnt){if(root==null) return 0;cnt[root.val]++;int ans=0;if(root.left==null&&root.right==null){int dif=0;for(int i=0;i<cnt.length;i++){if(cnt[i]%2==1) dif++;}ans=dif<=1?1:0;}else{ans=process(root.left,cnt)+process(root.right,cnt);}cnt[root.val]--;return ans;}
}
🥦 运行结果
💬 共勉
| 最后,我想和大家分享一句一直激励我的座右铭,希望可以与大家共勉! |


相关文章:

【LeetCode:1457. 二叉树中的伪回文路径 | 二叉树 + DFS +回文数】
🚀 算法题 🚀 🌲 算法刷题专栏 | 面试必备算法 | 面试高频算法 🍀 🌲 越难的东西,越要努力坚持,因为它具有很高的价值,算法就是这样✨ 🌲 作者简介:硕风和炜,…...

《golang设计模式》第三部分·行为型模式-06-备忘录模式(Memento)
文章目录 1. 概述1.1 角色1.2 类图 2. 代码示例2.1 设计2.2 代码2.3 类图 1. 概述 备忘录(Memento)用于在不破坏目标对象封装特性的基础上,将目标对象内部的状态存储到外部对象中,以备之后恢复状态时使用。 1.1 角色 Originato…...
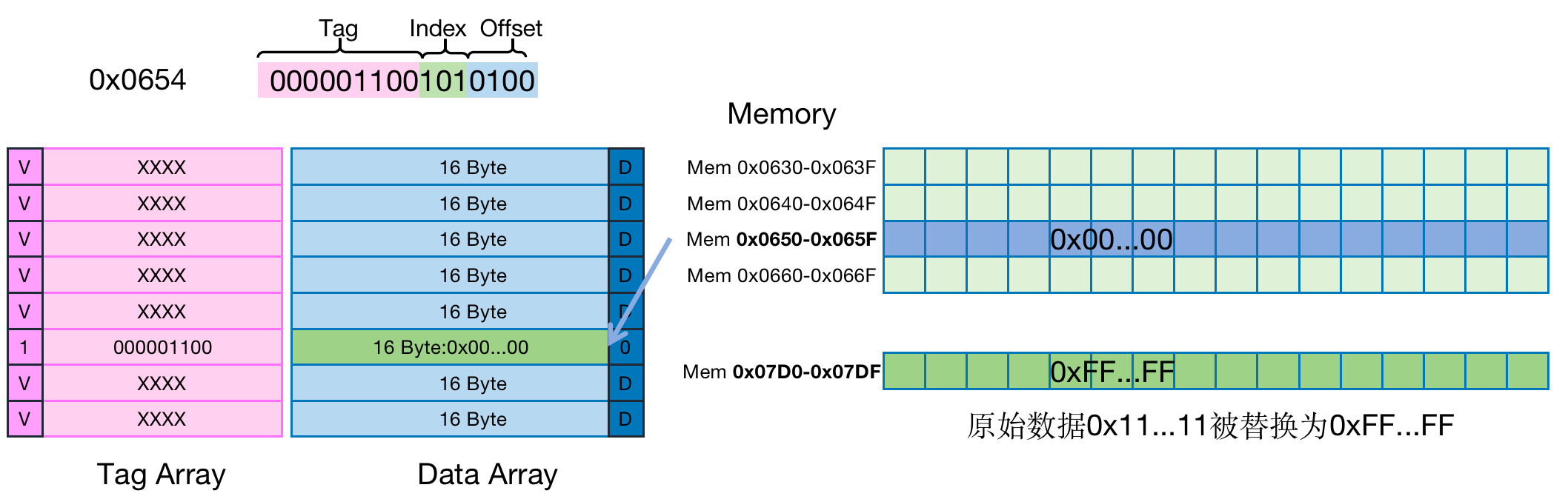
Cache学习(4):Cache分配策略Cache更新策略Cache逐出策略
Cache的数据流 常用名词 Allocation 分配Eviction 驱逐分配策略和更新策略分别为当产生Cache miss和Cache hit的时候数据流的具体行为 1 Cache分配策略(Cache Allocation Policy) Cache的分配策略是指不同情况下为数据分配Cache Line的不同行为。Cac…...

角色管理--产品经理岗
研发组织管理--角色管理--产品经理岗 定位 相对稳定和简单产品的独立产品打造者,复杂产品的辅助者 所需资质 校招新人,拥有灵性拥有基础的产品力(认知,设计,创新,推进,学习)Axur…...

SQL数据迁移实战:从产品层级信息到AB测试表
文章目录 创建表插入数据清空数据表数据迁移和筛选查询数据结论 创建表 首先,代码中定义了两个表格:dim_prod_hierarchy_info 和 app_abtest_product_info,都位于 test 数据库中。 dim_prod_hierarchy_info 表用于存储产品层级信息…...

VMware系列:VMware安装Android虚拟机
VMware系列:VMware安装Android虚拟机 一. 下载镜像这里提供了三种下载镜像方式,也就是三个下载链接,这里推荐百度网盘下载二. 使用VMware Workstation Pro 创建新的虚拟机操作系统应该可以选择任意一个,笔者只试过下图中,如果读者感兴趣可以多试几个,但笔者不保证每个都可…...
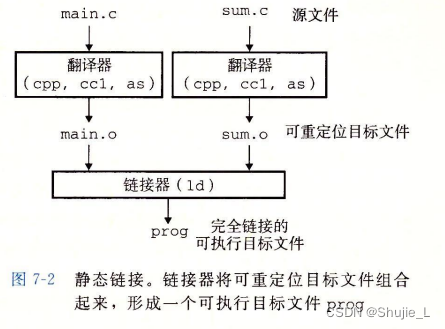
链接1:编译器驱动程序
文章目录 GNU编译器示例编译 GNU编译器 GNU编译器(GNU Compiler)是由自由软件基金会(Free Software Foundation,FSF)开发和维护的一套编译器集合。这些编译器主要用于编译各种编程语言的源代码,将其转换为…...

经典滑动窗口试题(二)
📘北尘_:个人主页 🌎个人专栏:《Linux操作系统》《经典算法试题 》《C》 《数据结构与算法》 ☀️走在路上,不忘来时的初心 文章目录 一、水果成篮1、题目讲解2、讲解算法思路3、代码实现 二、找到字符串中所有字母异位词1、题目…...
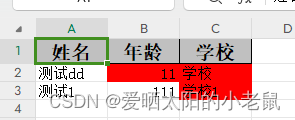
easyexcel指定sheet页动态给行列加背景色
需求 1、easyexcel,有多个sheet页,某些sheet页的行、列动态需要加背景色。 2、扩展支持cellStyle标记单元格超过64000 import com.alibaba.excel.metadata.CellData; import com.alibaba.excel.metadata.Head; import com.alibaba.excel.write.handler.…...

设计模式在实际业务中应用 - 模版方法
1. 业务背景 作者在工作中主要主导 A 业务线的系统建设,A 业务线主要是零售场景酒水的售卖与即时配送服务。为了方便运营在自研系统中对多平台商品进行管理而开发的三方平台商品管理功能,本次介绍的模版方法模式则是在该功能开发过程中的落地实践。 2.…...
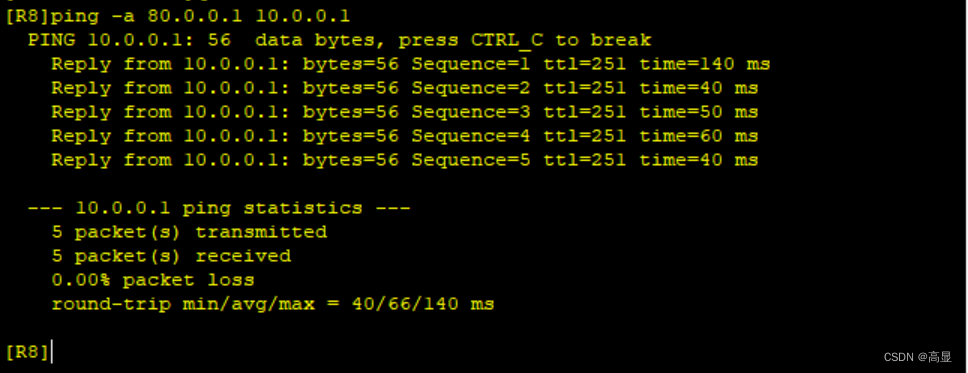
BGP综合实验
任务如下: 1.AS1存在两个环回,一个地址为192.168.1.0/24该地址不能在任何协议中宣告 AS3存在两个环回,一个地址为192.168.2.0/24该地址不能在任何协议中宣告,最终要求这两个环回可以互相通讯 2.整个AS2的IP地址为172.16.0.0/16&…...
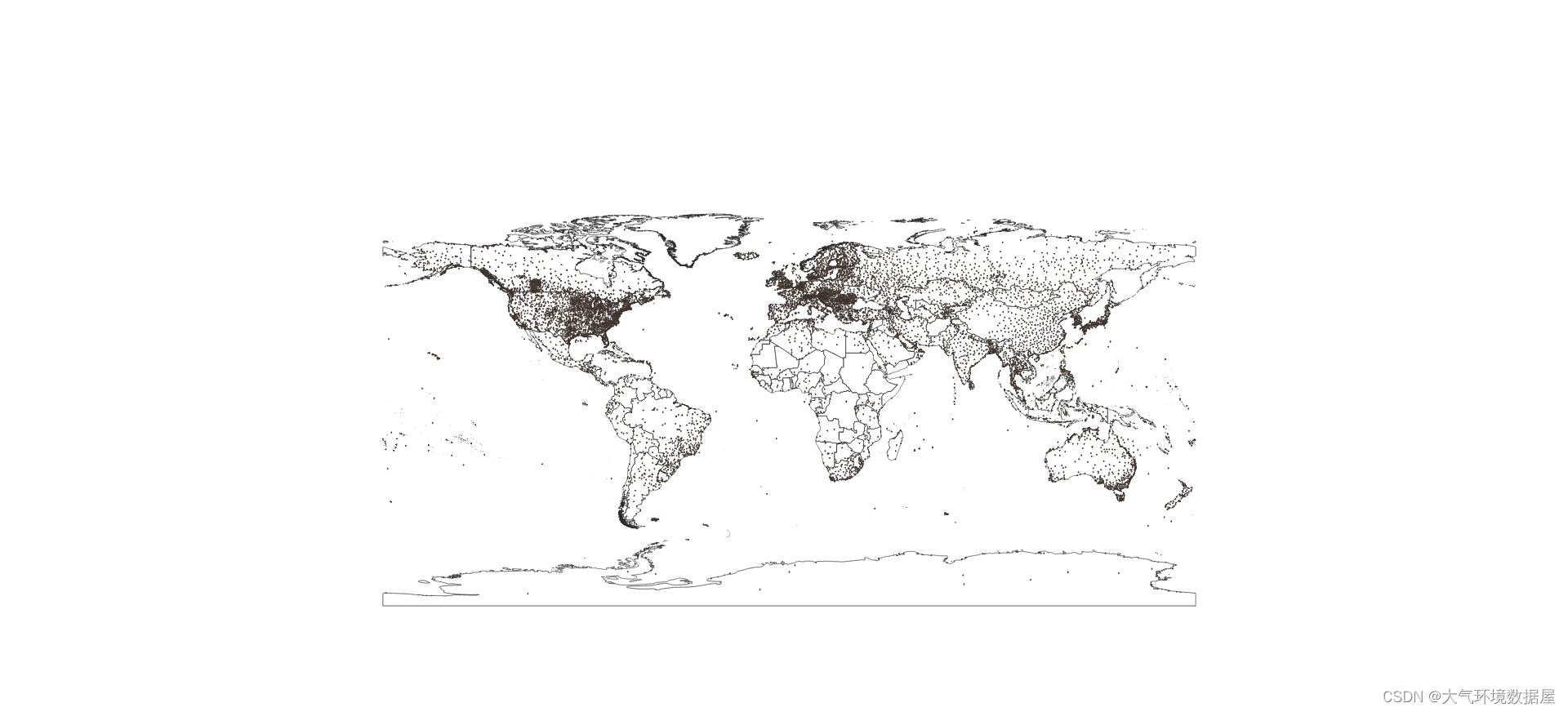
Global Surface Summary of the Day 全球逐日气象站点数据 GSOD数据集
数据名称 Global Surface Summary of the Day 数据内容 数据包含以下气象要素的日值观测数据: 气压:平均气压、海平面气压;气温:平均气温、日最高气温、日最低气温;湿度:露点温度(需自行换算…...
Harmony OS4开发入门
代码地址: https://gitee.com/BruceLeeAdmin/harmonyos/tree/master 项目目录介绍 ArkTS介绍 简单案例: State times: number 0/*数据类型:stringnumberany: 不确定类型,可以是任意类型*/State msg: string "hello"…...

.net core 事务
在 .NET Core 中,可以使用 Entity Framework Core 来实现事务处理。下面是一个简单的示例,展示了如何在 .NET Core 中使用 Entity Framework Core 来创建和执行事务: using System; using Microsoft.EntityFrameworkCore; using System.Tran…...
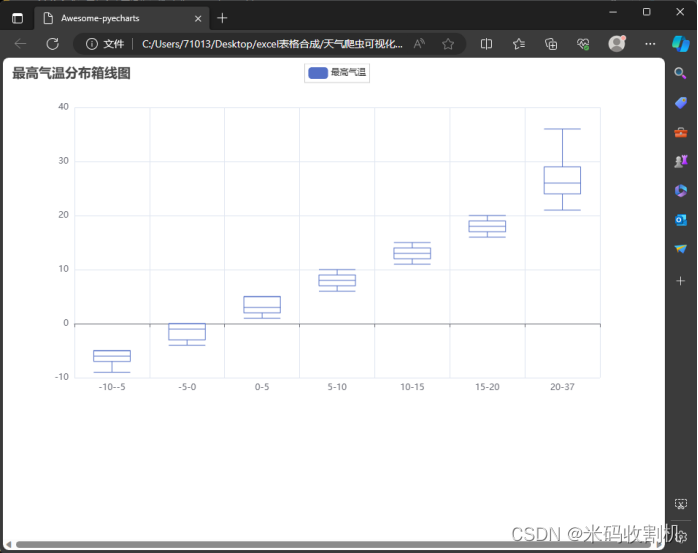
【Python】python天气数据抓取与数据分析(源码+论文)【独一无二】
👉博__主👈:米码收割机 👉技__能👈:C/Python语言 👉公众号👈:测试开发自动化【获取源码商业合作】 👉荣__誉👈:阿里云博客专家博主、5…...
MPPT工作流程及算法和硬件的选择
MPPT算法选择 目前,MPPT算法有开路电压比率(离线)、短路电流比率(离线)、观察调节(在线)、极限追踪控制法(在线)。 在光伏控制系统中,因为日照、温度等条件的变化,光伏电池的输出功率也是在不断变化的,为保证使得光伏电池的输出功…...

C#,《小白学程序》第十九课:随机数(Random)第六,随机生成任意长度的大数(BigInteger)
1 文本格式 using System; using System.Linq; using System.Text; using System.Collections.Generic; /// <summary> /// 大数的(加减乘除)四则运算、阶乘运算 /// 乘法计算包括小学生算法、Karatsuba和Toom-Cook3算法 /// 除法运算为 Truffer…...
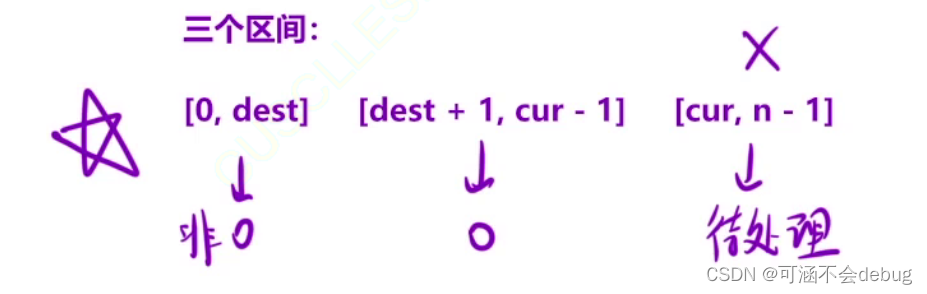
每日一练【移动零】
一、题目描述 283. 移动零 - 力扣(LeetCode) 给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。 请注意 ,必须在不复制数组的情况下原地对数组进行操作。 二、题目解析 可以…...
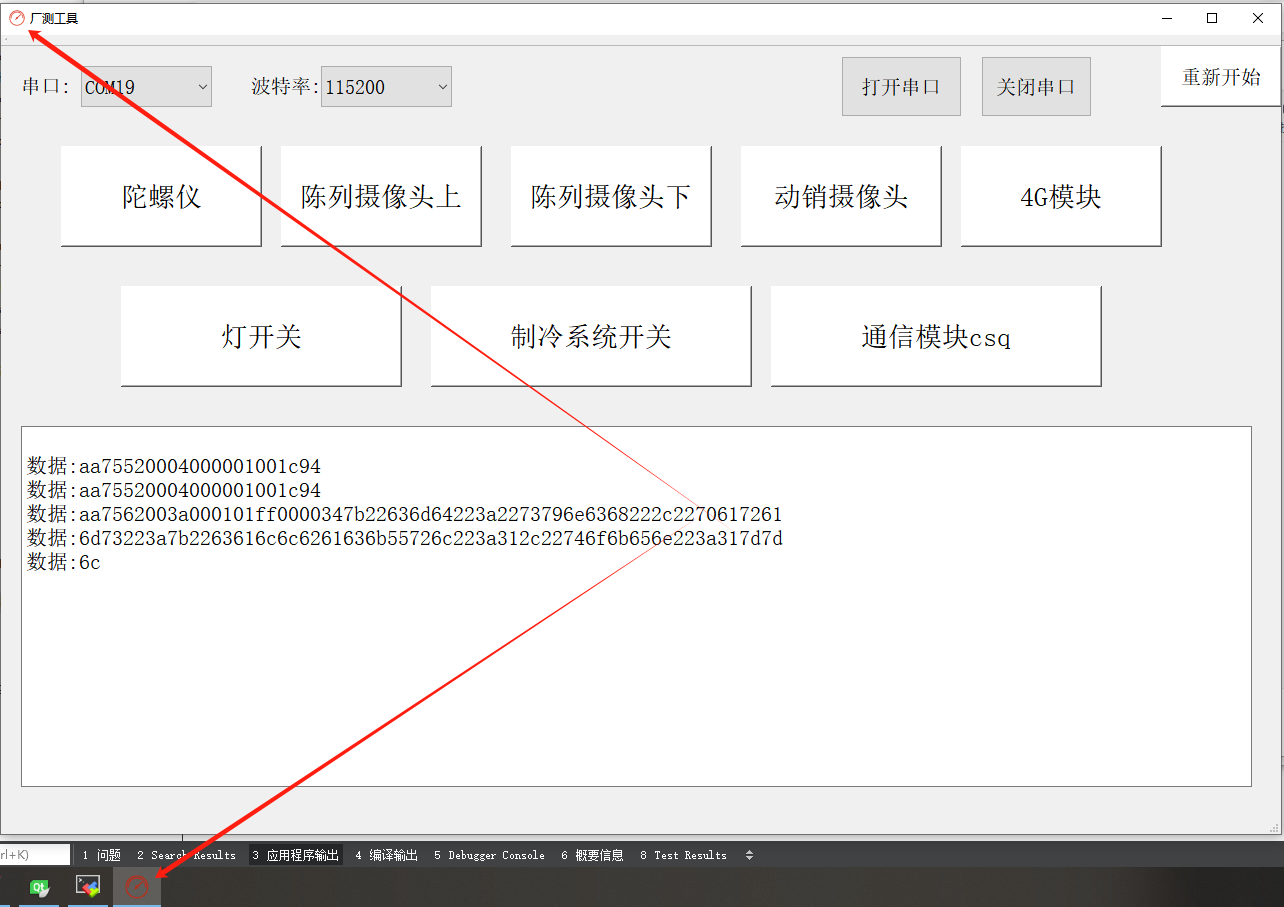
QT修改windowTitle的名字以及图片
1.修改名字:点击ui的QMainWindow,然后找到windowTitle的选项修改即可 2.修改windowTitle的图片,依旧是找到windowIcon,选择资源,这个资源可以是你放到qrc里面的图片也可以是外置的图片 3.然后运行就可以看到效果了...

C语言-指针讲解(3)
文章目录 1.字符指针变量1.1 字符指针变量类型是什么1.2字符指针变量的两种使用方法:1.3字符指针笔试题讲解1.3.1 代码解剖 2.数组指针变量2.1 什么是数组指针2.2 数组指针变量是什么?2.2.3 数组指针变量的举例 2.3数组指针和指针数组的区别是什么&#…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...
