leetCode 1080.根到叶路径上的不足节点 + 递归 + 图解
给你二叉树的根节点 root 和一个整数 limit ,请你同时删除树中所有 不足节点 ,并返回最终二叉树的根节点。假如通过节点 node 的每种可能的 “根-叶” 路径上值的总和全都小于给定的 limit,则该节点被称之为 不足节点 ,需要被删除。叶子节点,就是没有子节点的节点。
示例 1:
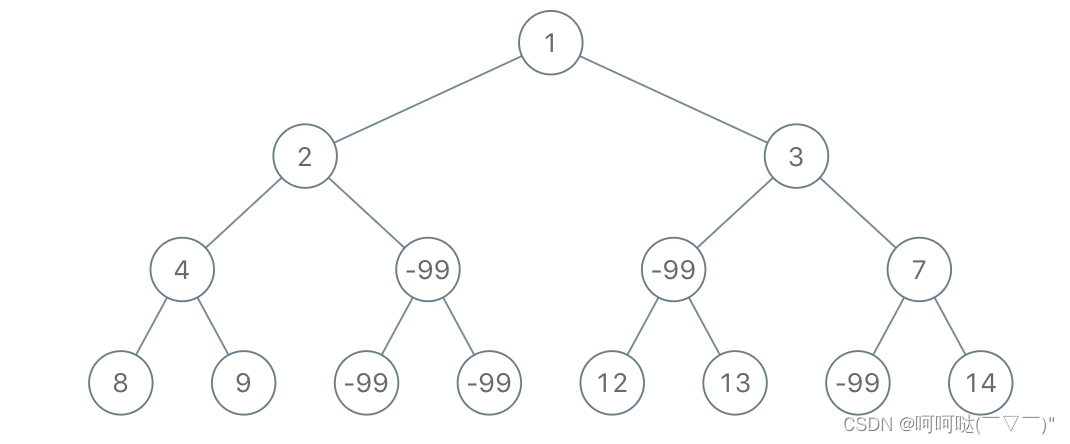
输入:root = [1,2,3,4,-99,-99,7,8,9,-99,-99,12,13,-99,14], limit = 1 输出:[1,2,3,4,null,null,7,8,9,null,14]
示例 2:
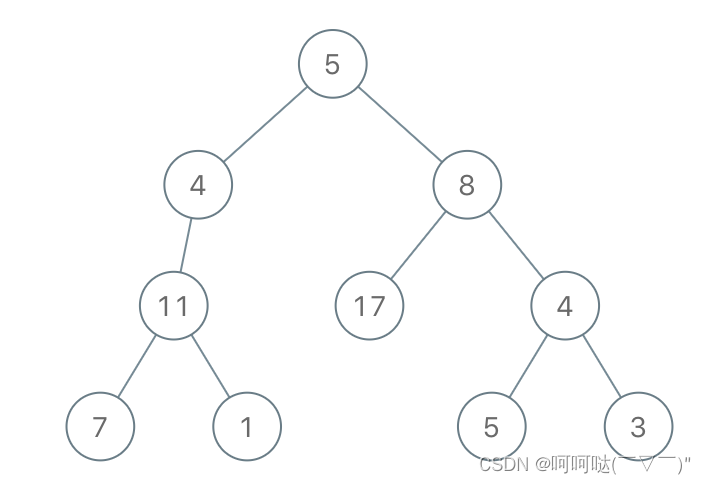
输入:root = [5,4,8,11,null,17,4,7,1,null,null,5,3], limit = 22 输出:[5,4,8,11,null,17,4,7,null,null,null,5]
示例 3:

输入:root = [1,2,-3,-5,null,4,null], limit = -1 输出:[1,null,-3,4]
方式1.添加一个递归参数 sumPath,表示从根到当前节点的路径和
(O_O)?疑惑:
- ① 叶子节点什么时候能删除?
- ② 非叶子节点若还有儿子未被删除,它能否被删除?
- ③ 非叶子节点的儿子都被删除,意味着什么?
思路和分析:
- ① 对于一个叶子节点(node),从根到这个叶子节点(leaf)的路径仅有一条,那么这条路径的元素和小于limit,就删掉该叶子节点
- ② 对于一个非叶子节点(node),若 node 还有儿子未被删除,那么 node 就不能被删除
- 反证法证明:设把 node 删除,那么经过 node 的所有路径和都小于 limit,这意味着经过 node 的儿子路径和也是小于 limit,那么 node 的儿子也应当被删除,矛盾!故 node 不能被删除
- ③ 对于一个非叶子节点(node)的儿子都被删除,意味着经过 node 的所有儿子的路径和都小于 limit。这等价于经过 node 的所有路径和都小于 limit,故 node 也应当被删除。
- 总结:当且仅当 node 的所有儿子都被删除,才可删除非叶节点 node
算法1:添加一个递归参数 sumPath,表示从根到当前节点的路径和
- ① 如果当前节点是叶子节点(leaf),且此时 sumPath < limit(说明从根到这个叶子节点的路径和小于limit),那么删除这个叶子节点
- ② 如果当前节点是非叶子节点(node),继续往下递归,node的左儿子(为leaf)时且经过 node 的左儿子路径和也是小于limit,就删除这个儿子;node的右儿子(为leaf)时且经过 node 的右儿子路径和也是小于limit,就删除这个儿子;
if(node->left && dfs(node->left,limit,sumPath)==false) { // 左node->left = nullptr;
}if(node->right && dfs(node->right,limit,sumPath)==false) { // 右node->right = nullptr;
}- ③ 如果当前节点是非叶子节点(node),且左右儿子都为空,那么就删除 node,返回 false ;否则,返回 true
return node->left || node->right;
C++代码:
class Solution {
public:bool dfs(TreeNode* node,int limit,int sumPath) {sumPath += node->val;if(node->left == node->right) {return sumPath>=limit;} if(node->left && dfs(node->left,limit,sumPath)==false) { // 左node->left = nullptr;}if(node->right && dfs(node->right,limit,sumPath)==false) { // 右node->right = nullptr;}return node->left || node->right;}TreeNode* sufficientSubset(TreeNode* root, int limit) {return dfs(root,limit,0) ?root:nullptr;}
};① 图解示例一:
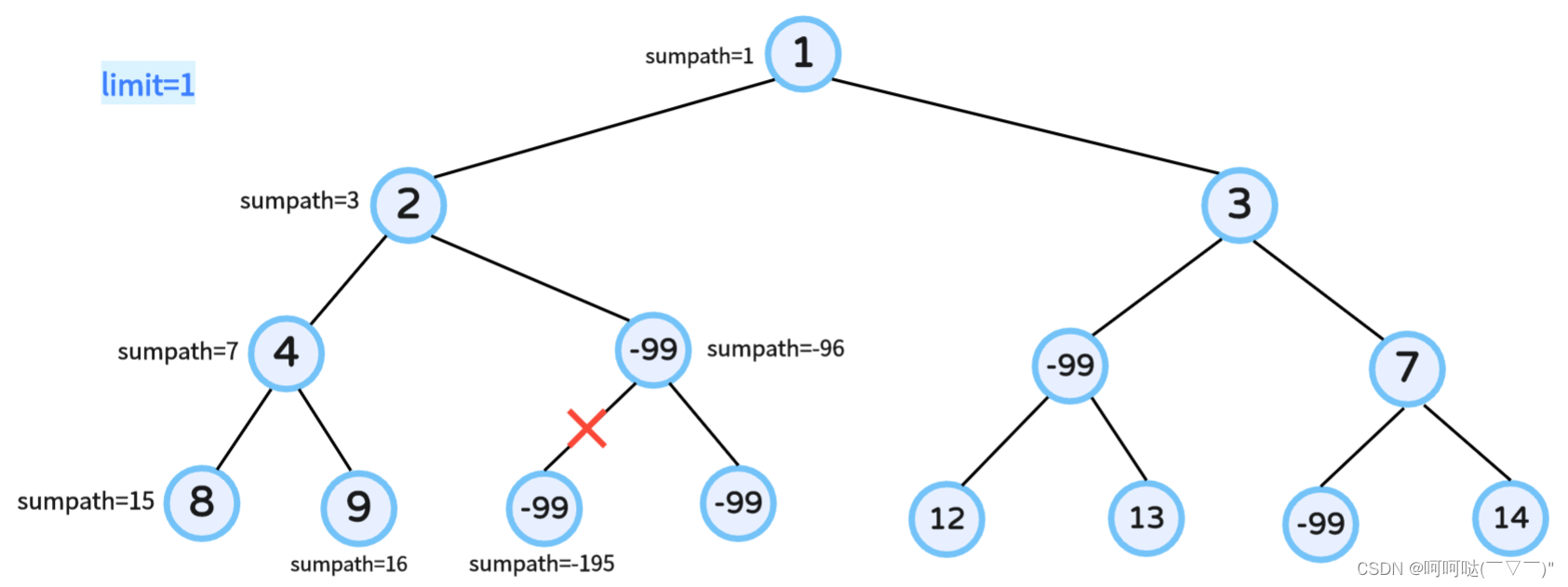
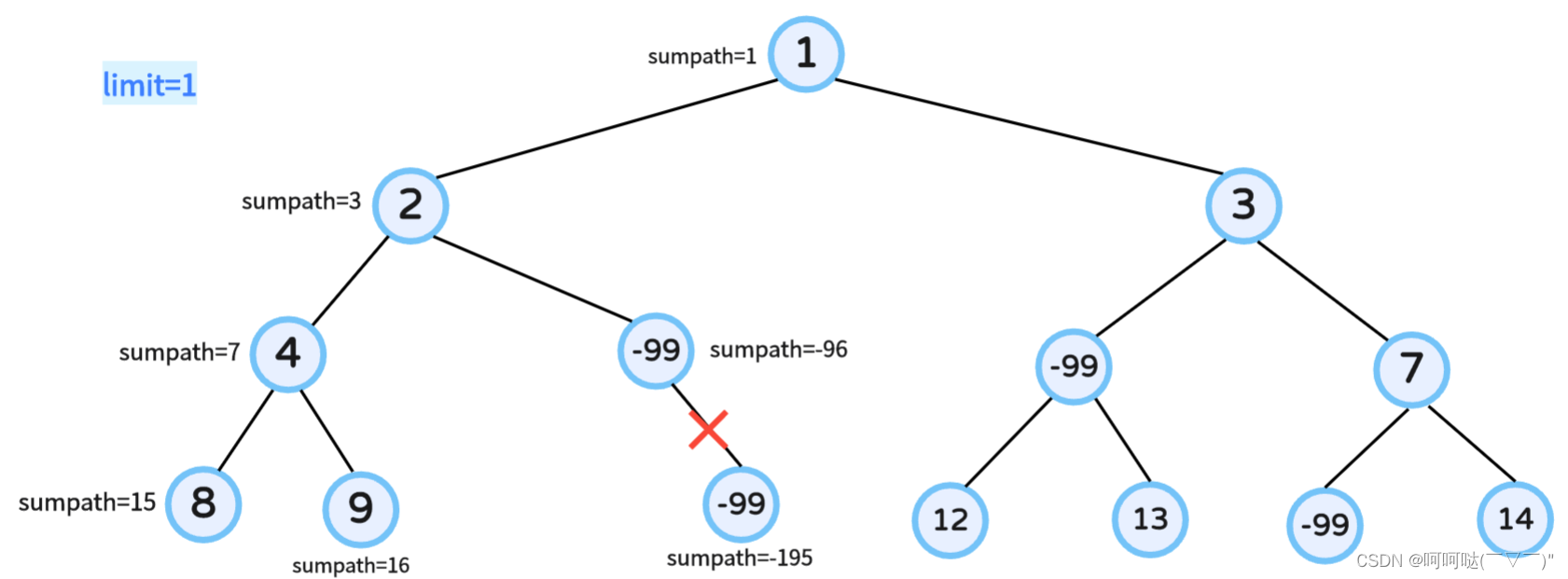
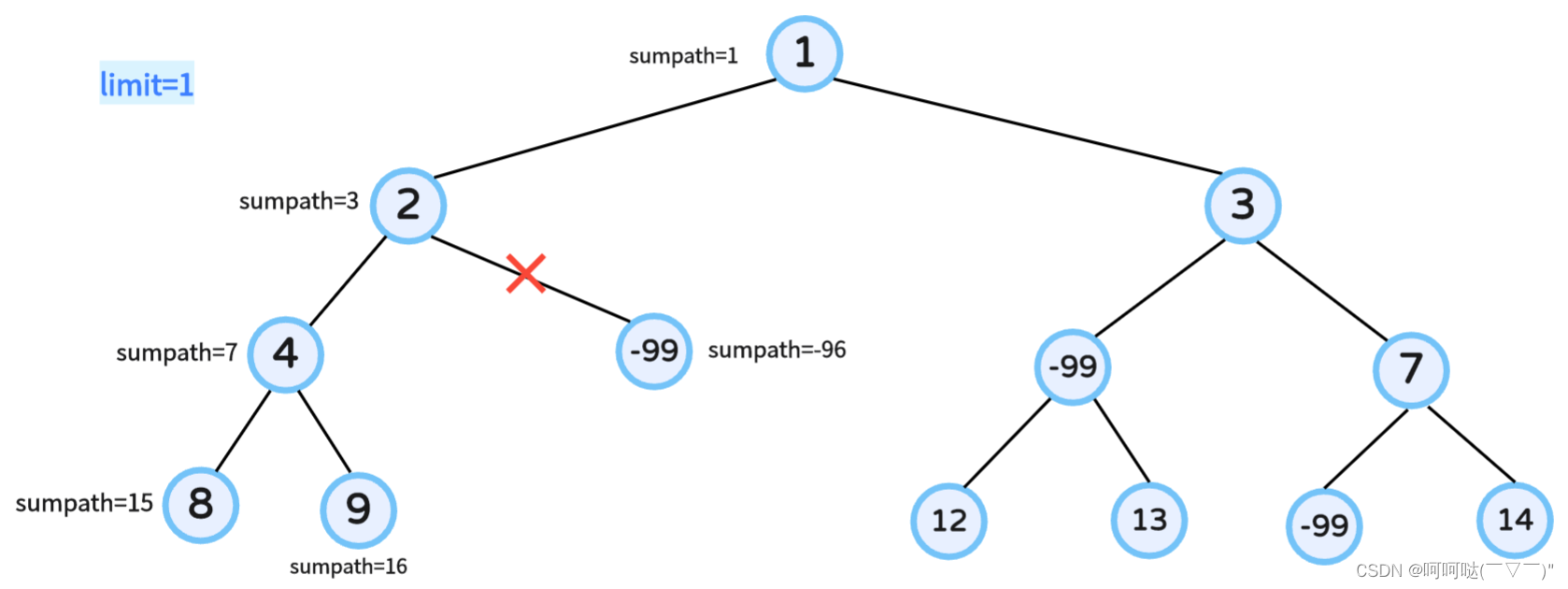
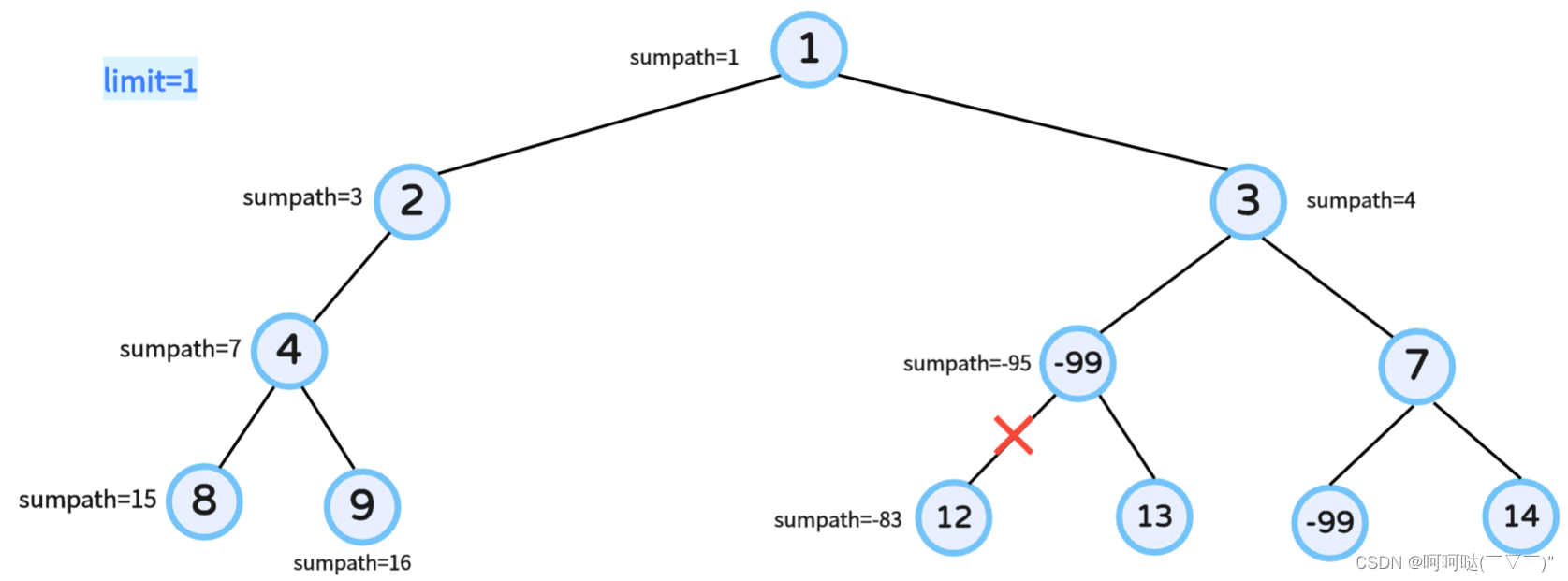
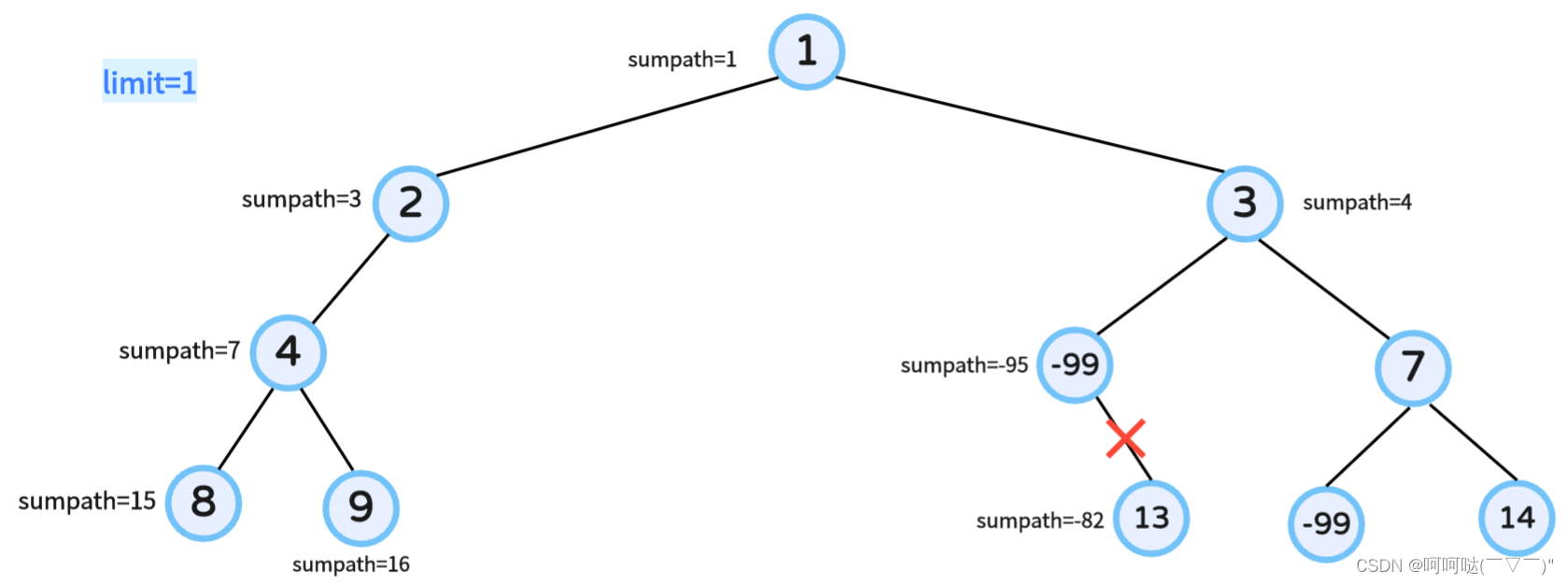

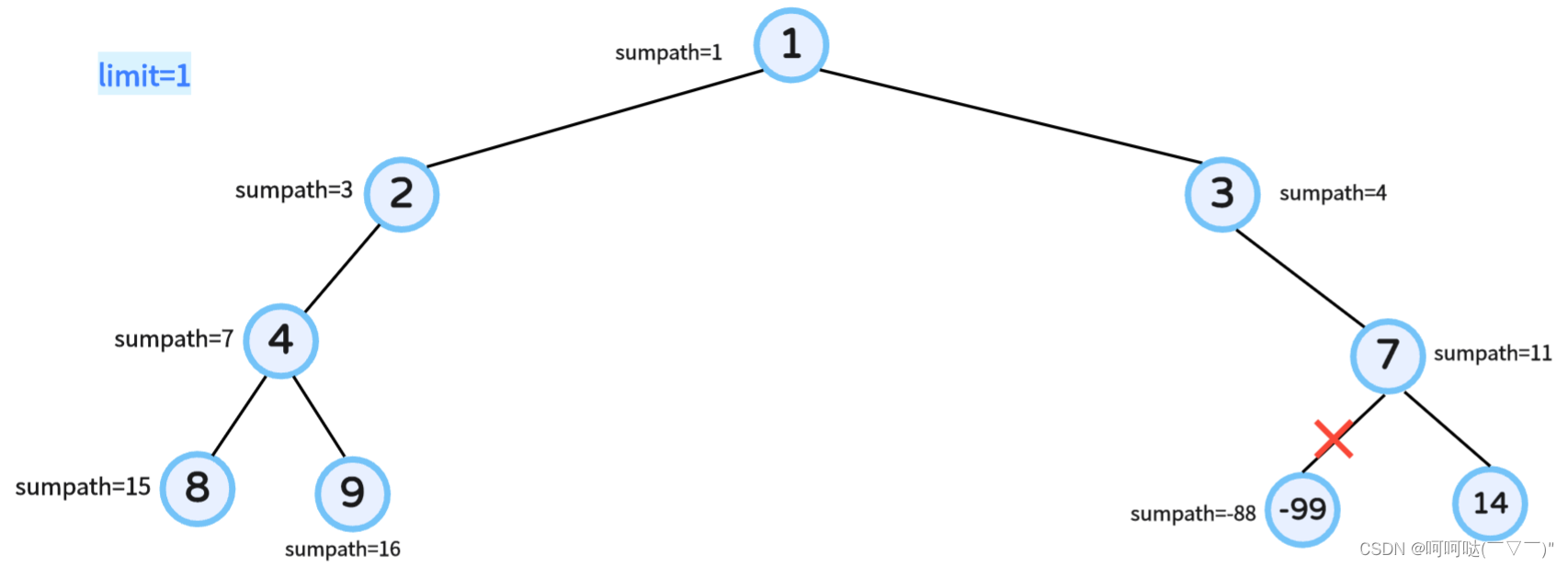
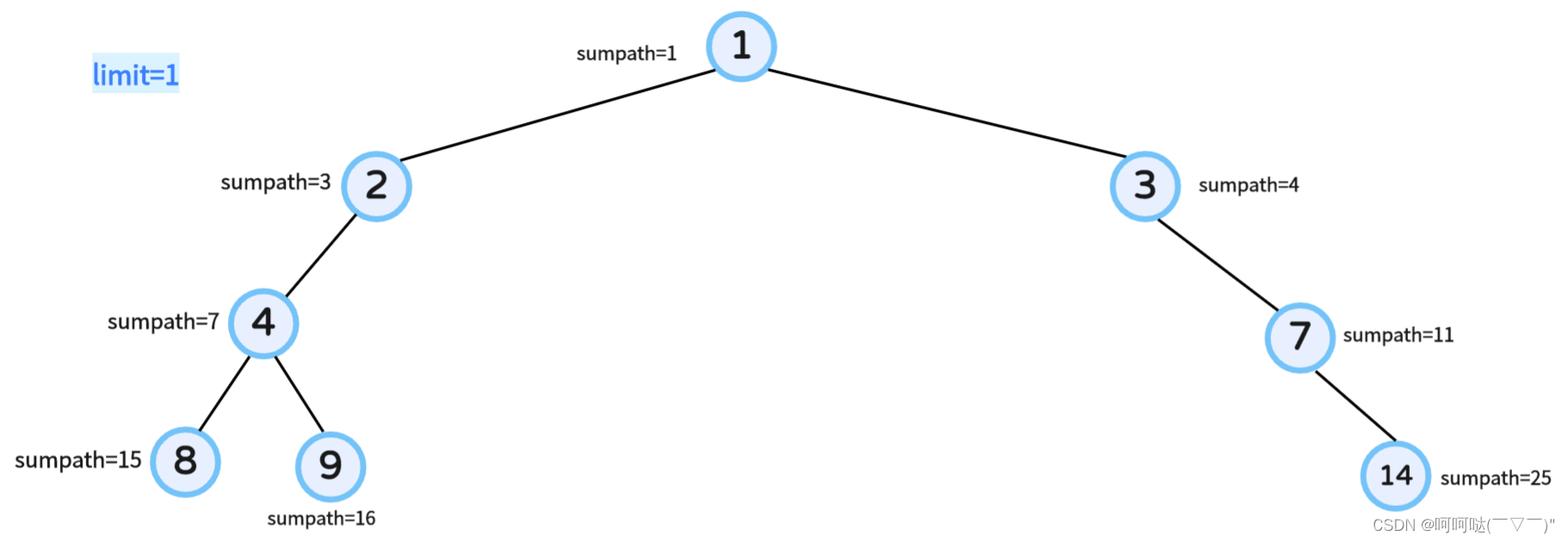
② 图解示例三:

方式2.从 limit 中减去当前节点值
- 先比方式1可以少一个参数 sumPath
class Solution {
public:bool dfs(TreeNode* node,int limit) {limit-=node->val;if(node->left == node->right) {return limit>0?false:true;} if(node->left && dfs(node->left,limit)==false) { // 左node->left = nullptr;}if(node->right && dfs(node->right,limit)==false) { // 右node->right = nullptr;}return node->left || node->right;}TreeNode* sufficientSubset(TreeNode* root, int limit) {return dfs(root,limit) ?root:nullptr;}
};方式3. 从 limit 中减去当前节点值(直接调用 sufficientSubset)
- 如果当前节点是叶子,且此时 limit > 0,说明从根到这个叶子的路径和小于 limit ,那么删除这个叶子
- 如果当前节点不是叶子,那么往下递归,更新它的左儿子为对左儿子调用 sufficientSubset 的结果,更新它的右儿子为对右儿子调用 sufficientSubset 的结果
- 如果左右儿子都为空,那么就删除当前节点,返回空;否则不删,返回当前节点
此段文字来自以下作者
作者:灵茶山艾府
链接:https://leetcode.cn/problems/insufficient-nodes-in-root-to-leaf-paths/description/

class Solution {
public:TreeNode* sufficientSubset(TreeNode* root, int limit) {limit-=root->val;if(root->left == root->right) { // root 是叶子return limit > 0 ? nullptr : root;} if(root->left) { // 左root->left = sufficientSubset(root->left,limit);}if(root->right) { // 右root->right = sufficientSubset(root->right,limit);}// 如果有儿子没被删除,就不删 root,否则删 rootreturn root->left || root->right ?root:nullptr;}
};(嘻嘻,仅供参考) 自己又写了一个版本:
class Solution {
public:TreeNode* dfs(TreeNode* node,int limit,int sumPath) {sumPath += node->val;if(node->left == node->right) {return sumPath>=limit? node : nullptr;} if(node->left) { // 左node->left = dfs(node->left,limit,sumPath);}if(node->right) { // 右node->right = dfs(node->right,limit,sumPath);}return node->left || node->right ?node:nullptr;}TreeNode* sufficientSubset(TreeNode* root, int limit) {return dfs(root,limit,0) ? root:nullptr;}
};参考和推荐文章:
1080. 根到叶路径上的不足节点 - 力扣(LeetCode)![]() https://leetcode.cn/problems/insufficient-nodes-in-root-to-leaf-paths/solutions/2278769/jian-ji-xie-fa-diao-yong-zi-shen-pythonj-64lf/
https://leetcode.cn/problems/insufficient-nodes-in-root-to-leaf-paths/solutions/2278769/jian-ji-xie-fa-diao-yong-zi-shen-pythonj-64lf/
相关文章:
leetCode 1080.根到叶路径上的不足节点 + 递归 + 图解
给你二叉树的根节点 root 和一个整数 limit ,请你同时删除树中所有 不足节点 ,并返回最终二叉树的根节点。假如通过节点 node 的每种可能的 “根-叶” 路径上值的总和全都小于给定的 limit,则该节点被称之为 不足节点 ,需要被删除…...

C++基础 -10- 类
类的格式 public:公共成员 类外可访问 protected:保护成员 类外不可访问 private:私有成员 类外不可访问 class base {public:int a;protected:int b;private:int c;};...

【软件测试】性能测试相关指标
性能测试 了解性能测试相关指标 1.什么是做性能测试 1.1 生活中遇到的软件性能问题 软件用着用着就不能用了,一看热搜,发现该软件的服务器崩崩溃了。 1.2 性能测试定义 测试人员借助性能测试工具,模拟系统在不同场景下,对应…...

Leetcode 2943. Maximize Area of Square Hole in Grid
Leetcode 2943. Maximize Area of Square Hole in Grid 1. 解题思路2. 代码实现 题目链接:2943. Maximize Area of Square Hole in Grid 1. 解题思路 这一题的话其实横轴和竖轴可以分开来独立考察,因为两者互不影响,我们最终的答案一定是两…...

qt 简单了解QHBoxLayout QVBoxLayout QFormLayout水平,垂直,表单布局管理器.
QHBoxLayout水平布局,QVBoxLayout垂直布局,QFormLayout表单布局管理器,是常用的布局管理器,是用代码编写应用界面必不可少的功能类. 1.tips 这里值得注意的是,2个单选按钮(QRadioButton)同时放进一个水平布局管理器(QHBoxLayout)中,相当于放进了一个分组器中,此时,2个单选按钮…...

springboot中4级配置文件优先级
springboot中4级配置文件优先级...

Python(八十九)函数的参数的内存分析
❤️ 专栏简介:本专栏记录了我个人从零开始学习Python编程的过程。在这个专栏中,我将分享我在学习Python的过程中的学习笔记、学习路线以及各个知识点。 ☀️ 专栏适用人群 :本专栏适用于希望学习Python编程的初学者和有一定编程基础的人。无…...
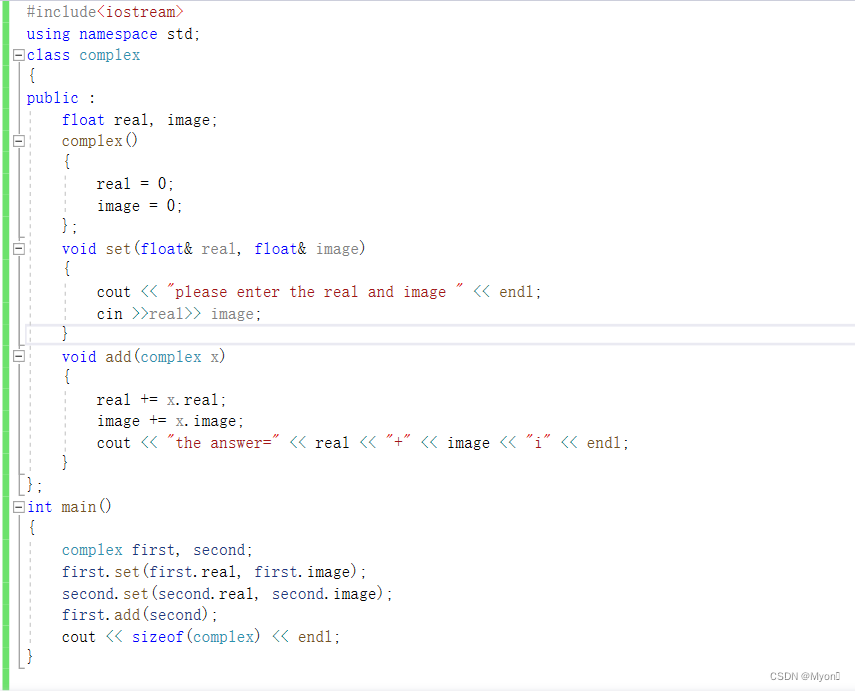
西南科技大学C++程序设计实验二(类与对象一)
C++最大的特点就是面向对象,掌握它的几种基本性质还是好理解的,可以看我C++专栏的期末速成,希望对你们学习C++有帮助。 一、实验目的 1.理解简单类的定义、说明与使用 2.理解类中不同属性数据成员的访问特点 3.理解构造函数、析构函数的作用 重点:掌握类的定义与实现,…...

代码随想录二刷 |哈希表 |四数之和
代码随想录二刷 |哈希表 |四数之和 题目描述解题思路 & 代码实现 题目描述 18.四数之和 给你一个由 n 个整数组成的数组 nums ,和一个目标值 target 。请你找出并返回满足下述全部条件且不重复的四元组 [nums[a], nums[b], nums[c], nu…...
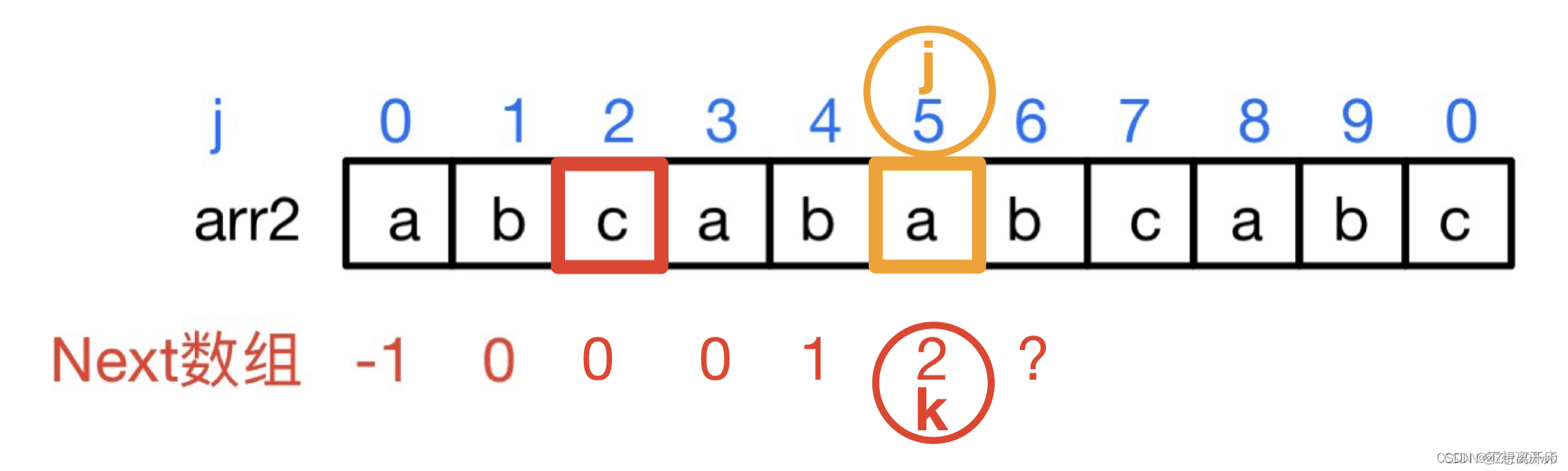
KMP算法【数据结构】
KMP算法 KMP算法是一种改进的字符串匹配算法 Next[j] k :一个用来存放子串返回位置的数组,回溯的位置用字母k来表示。其实就是从匹配失败位置,找到他前面的字符串的最大前后相等子串长度。默认第一个k值为-1(Next[0] -1),第二个k值为0(Next[1] 0),我…...

测开笔记--Typescript: 文件复制到指定目录
开发背景: 自动化开发语言使用的是TypeScript;框架用的是playwright。有个测试脚本需要先将几个文件复制粘贴到新建的项目文件夹下,系统会读取该文件,然后生成页面信息。 关键字:文件复制粘贴; 新建的项目…...

数字滚动vue-count-to
数字滚动 下载插件 npm i vue-count-to 使用 start-val 起始值,表示从什么值开始滚 end-val 终点值,表示要滚到多大值 duration 滚动事件,表示用多长时间来滚动 <countTo :start-val"0" :end-val"228" :duration&quo…...

扩散模型实战(十一):剖析Stable Diffusion Pipeline各个组件
推荐阅读列表: 扩散模型实战(一):基本原理介绍 扩散模型实战(二):扩散模型的发展 扩散模型实战(三):扩散模型的应用 扩散模型实战(四ÿ…...
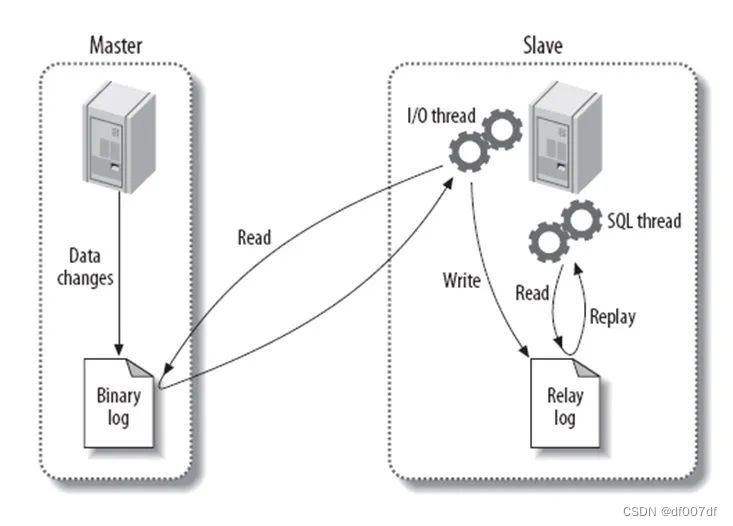
Mysql面试题总结
数据库三大范式是什么 第一范式:每个列都不可以再拆分。 第二范式:在第一范式的基础上,非主键列完全依赖于主键,而不能是依赖于主键的一部分。 第三范式:在第二范式的基础上,非主键列只依赖于主键&#…...

学习知识随笔(Django)
文章目录 MVC与MTV模型MVCMTV Django目录结构Django请求生命周期流程图路由控制路由是什么路由匹配反向解析路由分发 视图层视图函数语法reqeust对象属性reqeust对象方法 MVC与MTV模型 MVC Web服务器开发领域里著名的MVC模式,所谓MVC就是把Web应用分为模型(M&#…...
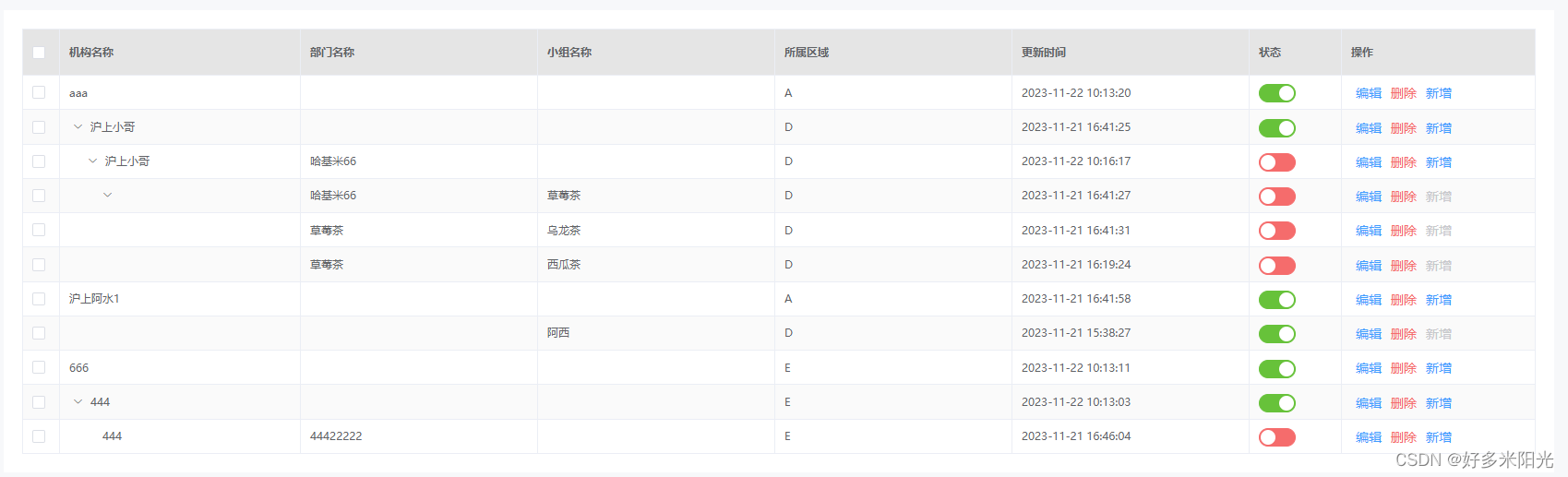
基于element自动表格
需求是根据JSON文件生成表格,包含配置和自动props属性以及过滤器; 数据示例: 表格设置: /*** 表格表头信息* chineseToPinYin: 这是封装的根据中文汉字转换为拼音的方法* prop: 表头字段名* filter: 数据过滤器* label: 表头显示…...
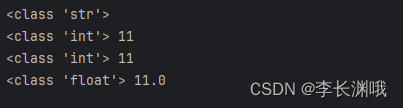
Python基础语法之学习数据转换
Python基础语法之学习数据转换 一、代码二、效果 一、代码 #数字转换成字符串 num_str str(11) print(type(num_str))#字符串转整数 numint("11") print(type(num),num)#浮点数转整数 float_num int(11.1) print(type(float_num),float_num)#整数转浮点数 num_flo…...
最新AI创作系统ChatGPT网站运营源码、支持GPT-4-Turbo模型,图片对话识图理解,支持DALL-E3文生图
一、AI创作系统 SparkAi是目前国内一款的ChatGPT对接OpenAI软件系统。那么如何搭建部署AI创作ChatGPT?小编这里写一个详细图文教程吧!本系统使用NestjsVueTypescript框架技术,持续集成AI能力到本系统。支持OpenAI DALL-E3文生图,…...

Kotlin中常见的List使用
文章目录 1.filter2.map3.count4.first,last5.any,all,none6.find,findLast7.indexOf()和lastIndexOf()查找元素下标8.Slice切片9.Take()和drop()获取指定长度 1.filter filter 就像其本意一样,可以通过 filter 对 Kotlin list 进行过滤。 fun main() …...
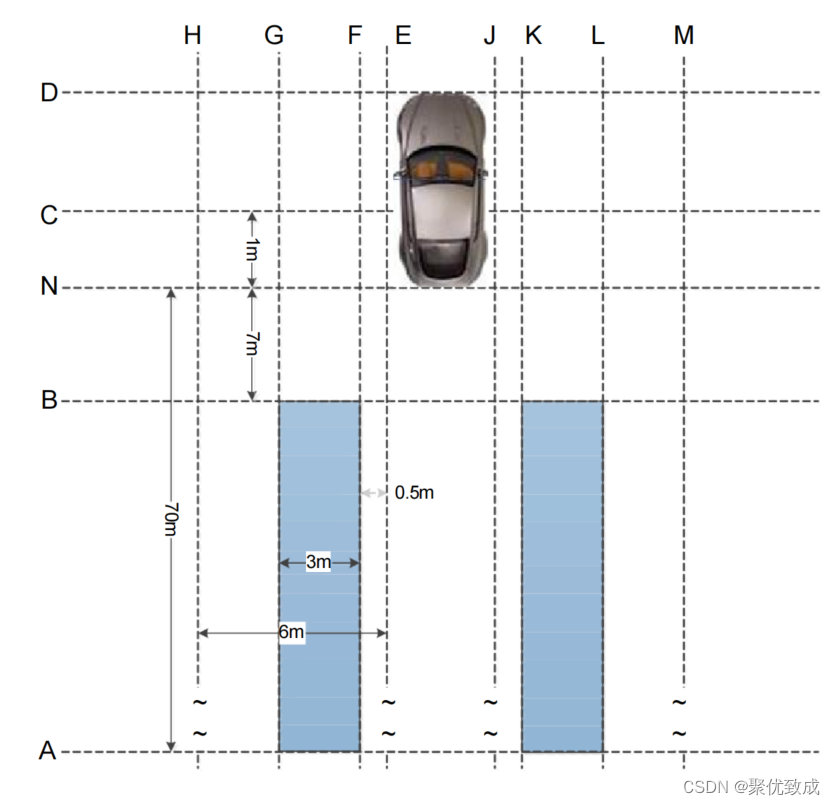
汽车电子 -- 车载ADAS之LCA(变道辅助系统)
相关法规文件: LCA: ISO 17387-2008 Intelligent transport systems — Lane change decision aid systems 一、变道辅助系统 LCA (Lane Change Assist) LCA 系统(变道辅助系统)监测后方相邻车道区域,如果有车辆在后…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...
