京东数据分析(京东大数据采集):2023年线上珍珠市场销售数据采集
在珠宝首饰市场,从黄金到钻石,如今年轻人的新风潮又转向了珍珠。珍珠热潮并非刚刚兴起,早在前两年,抖音、快手等短视频台的珍珠开蚌直播内容,就掀起了一波珍珠热潮。
此后,随着珍珠饰品被越来越多社交平台的KOL分享,珍珠在电商平台的销售量也水涨船高。根据鲸参谋电商数据分析平台的相关数据显示,今年(截至10月份)京东平台上珍珠饰品的销量为60万+,环比增长约129%,同比增长约138%;销售额将近2.3亿,环比增长约62%,同比增长约64%。
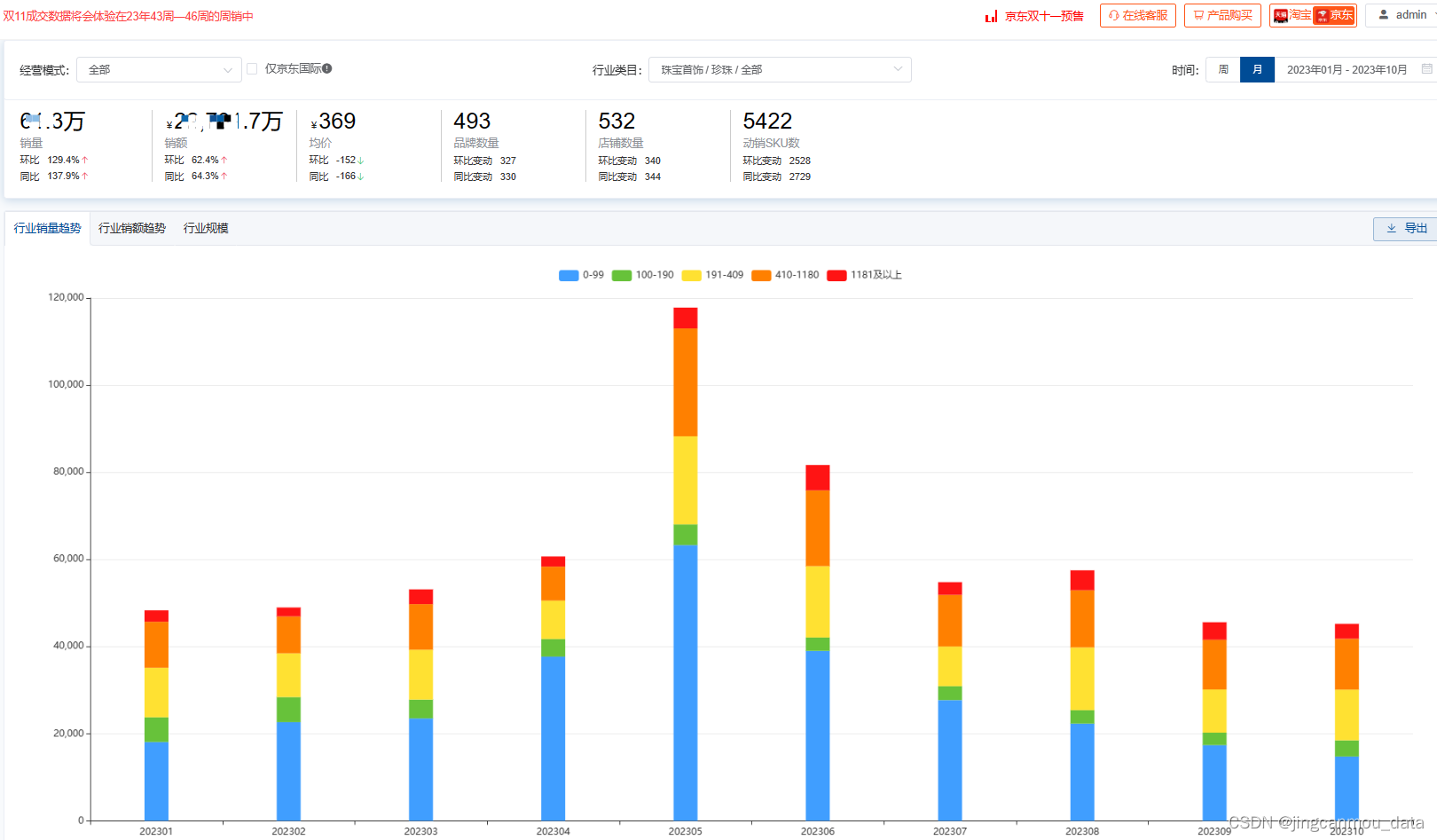
*数据源于鲸参谋-行业趋势分析(来自公开渠道获取与统计,数据仅供参考)
珍珠市场中的热销饰品主要有珍珠项链、耳饰、手链、吊坠、戒指、胸针及裸珠等。目前,市场占比排名第一的细分类目便是珍珠项链,其次是珍珠耳饰。
鲸参谋数据显示,截至今年10月份,京东平台珍珠项链的销售额为1.4亿+,同比增长约60%,市场占比为63%;珍珠耳饰的销售额将近4600万,同比增长约146%,市占在20%左右。
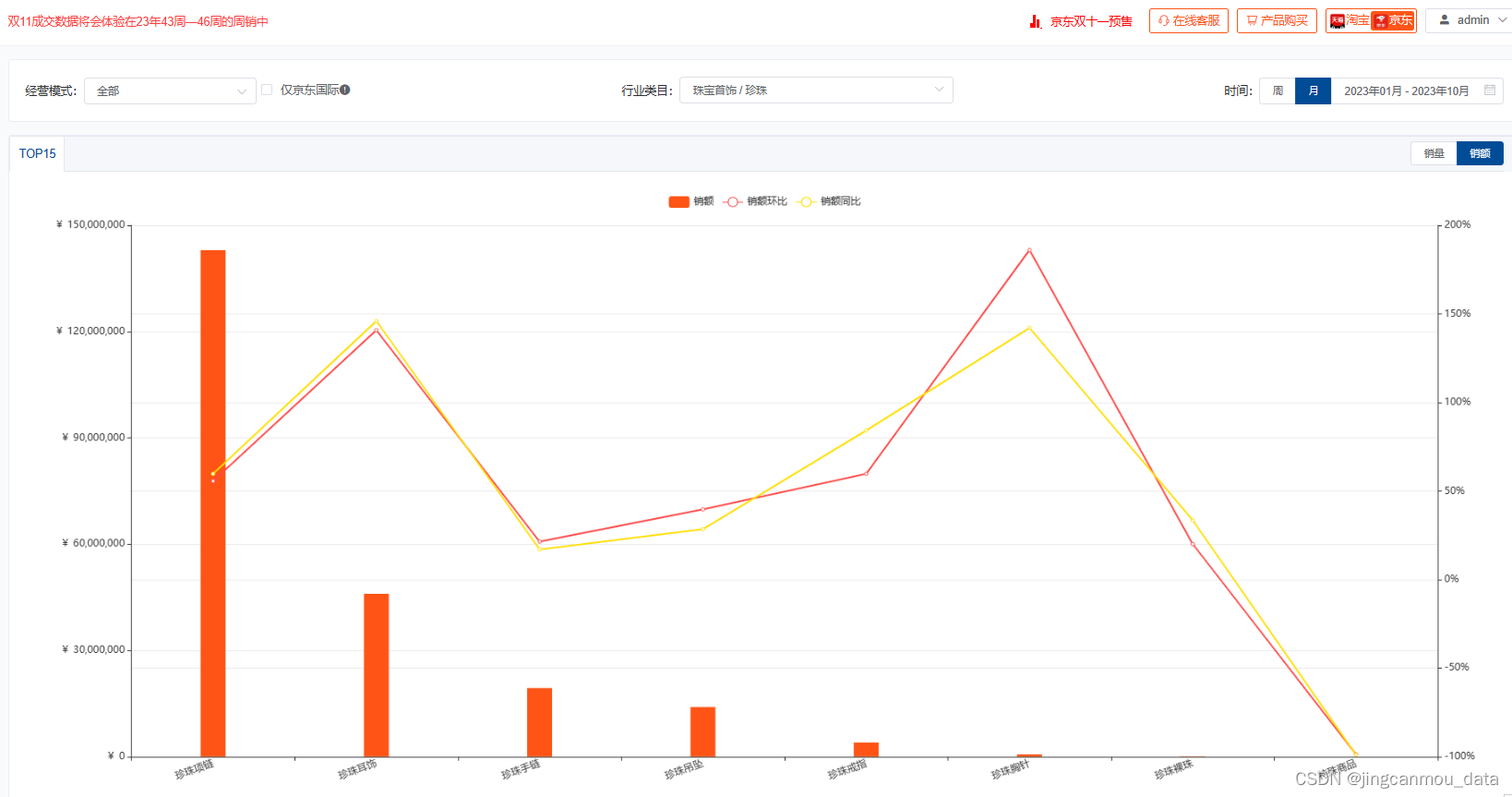
*数据源于鲸参谋-类目排行分析(来自公开渠道获取与统计,数据仅供参考)
从价格角度看,在珍珠饰品市场中,中高价产品的受欢迎程度较高。鲸参谋数据显示,截至今年10月份,“410元-1180元”“1181元及以上”这两个价格段产品的销售额分别为8400万+和8100万,占比分别约37%和36%。
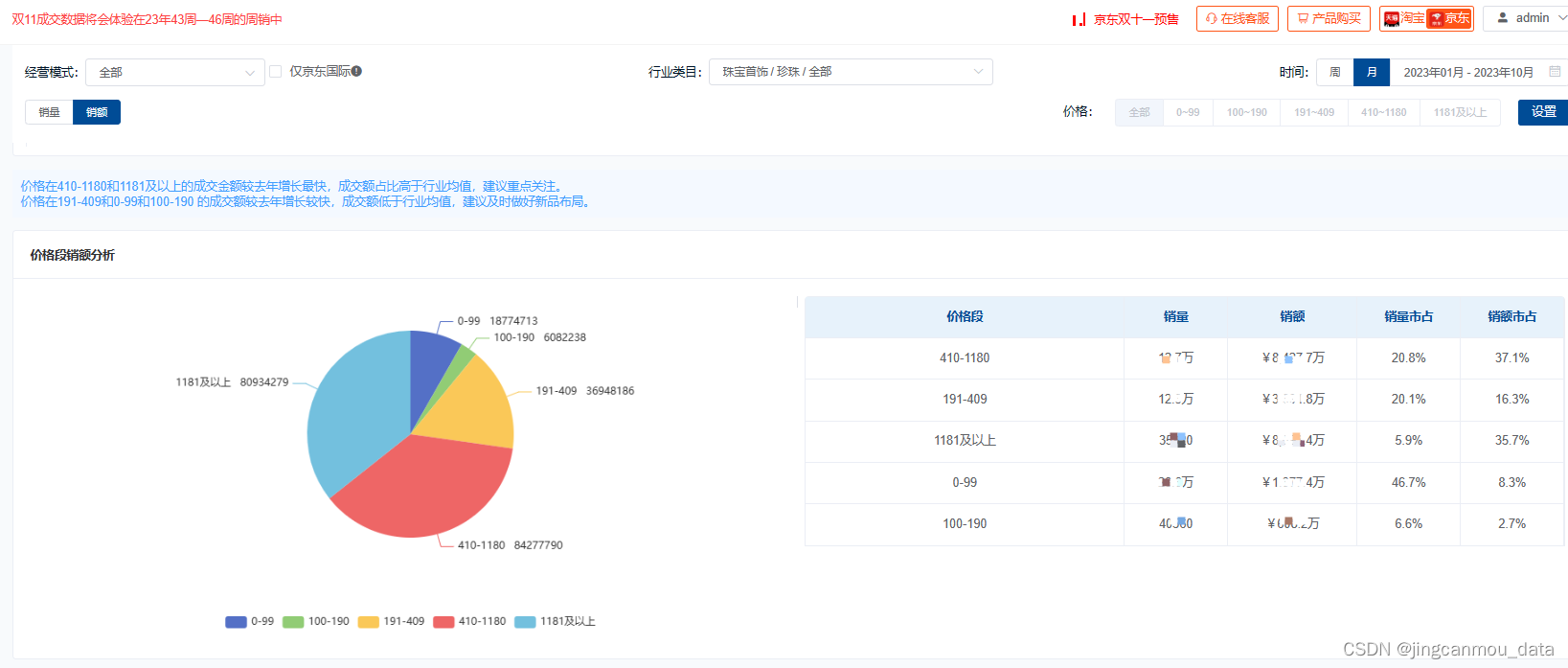
*数据源于鲸参谋-价格段分析(来自公开渠道获取与统计,数据仅供参考)
从品牌角度来看,在珍珠饰品市场中,市占较高的品牌有京润、周六福和珍珠皇后。
来看这些品牌的具体销售数据,鲸参谋数据显示,今年1月至10月,京润珍珠的销售额为4800万+,占比约21%;周六福珍珠饰品销售额为3500万+,市场占比约16%;珍珠皇后的市场占比约2400万+,占比约11%。
此外,珍珠饰品的热销TOP10品牌榜单中还有黛米、GiO、helas、周大福、meluxe、六福珠宝和大溪地等品牌,品牌市占均在4%至9%之间。
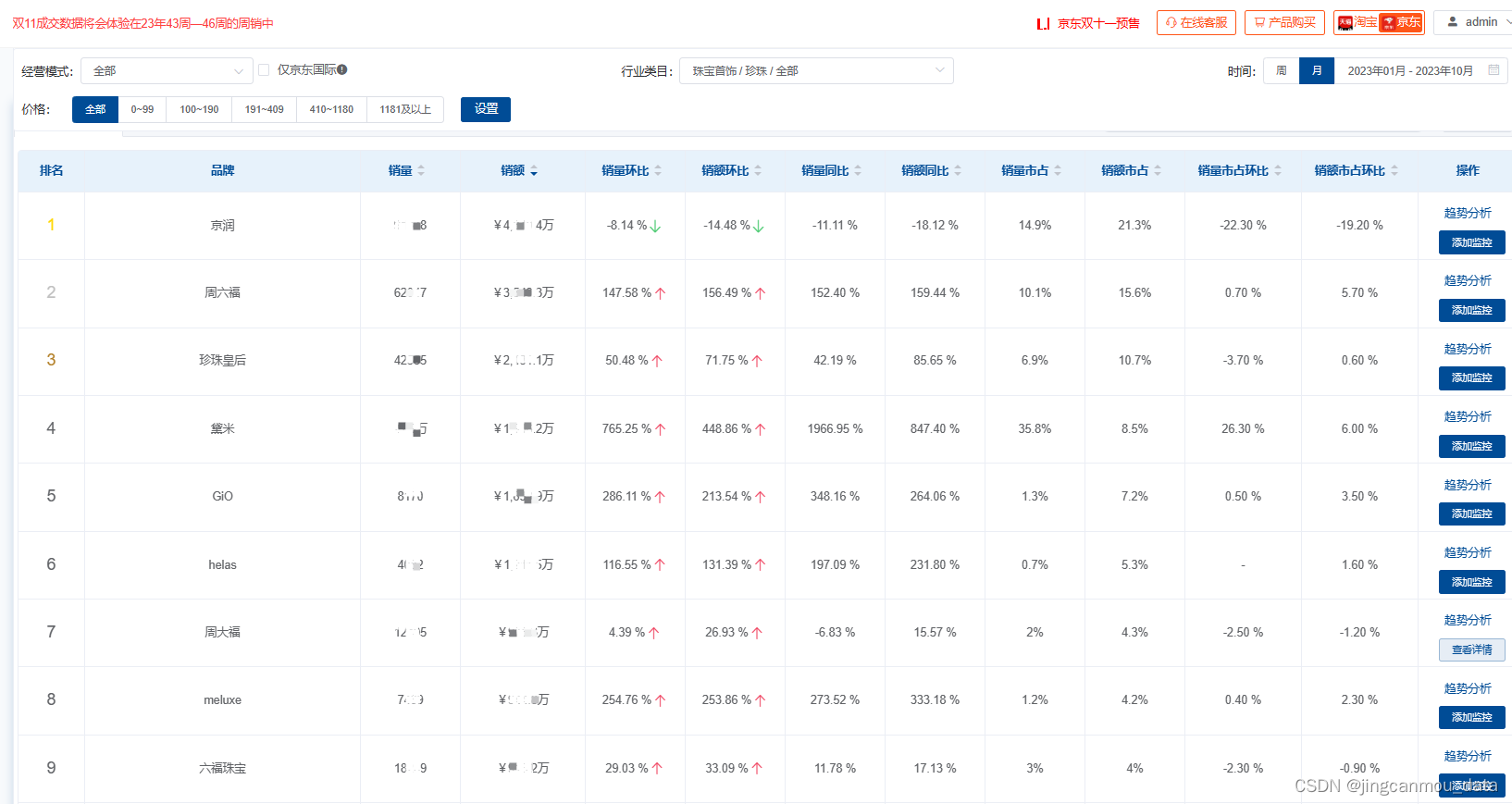
*数据源于鲸参谋-品牌排行分析(来自公开渠道获取与统计,数据仅供参考)
虽然珍珠市场中也有市场占比较高的头部品牌,但整体而言,相较其他珠宝首饰,珍珠市场的品牌化程度仍有待提升。如当消费者谈及黄金,脑海里很快就会涌现周大福、老凤祥等品牌,但提及珍珠,很多人却很难说出主营珍珠的品牌,对珍珠的印象还停留在散珠、串珠上。
因此,对于珍珠厂商而言,若想要在赛道中杀出重围,不仅要在供应侧、销售侧做好充足的准备,同时也应在品牌塑造上发力。
鲸参谋数据来源于公开渠道,数据获取与统计可能存在不完整,仅供参考。
如想要查看京东(淘宝/天猫)全品类的销售数据(行业/品牌/店铺/商品/监控),欢迎搜索“鲸参谋电商数据”,或者直接评论留言和私信(也可接口对接)~
相关文章:

京东数据分析(京东大数据采集):2023年线上珍珠市场销售数据采集
在珠宝首饰市场,从黄金到钻石,如今年轻人的新风潮又转向了珍珠。珍珠热潮并非刚刚兴起,早在前两年,抖音、快手等短视频台的珍珠开蚌直播内容,就掀起了一波珍珠热潮。 此后,随着珍珠饰品被越来越多社交平台的…...
亚信科技AntDB数据库与库瀚存储方案完成兼容性互认证
近日,亚信科技AntDB数据库与苏州库瀚信息科技有限公司自主研发的RISC-V数据库存储解决方案进行了产品兼容测试。经过双方团队的严格测试,亚信科技AntDB数据库与库瀚数据库存储解决方案完全兼容、运行稳定。除高可用性测试外,双方进一步开展TP…...

现代C++之万能引用、完美转发、引用折叠
现代C之万能引用、完美转发、引用折叠 0.导语1.问题引入2.引入万能引用3.万能引用出现场合4.理解左值与右值4.1 精简版4.2 完整版4.3 生命周期延长4.4 生命周期延长应用5.区分万能引用6.表达式的左右值性与类型无关7.引用折叠和完美转发7.1 引用折叠之本质细节7.2 示例与使用7.…...
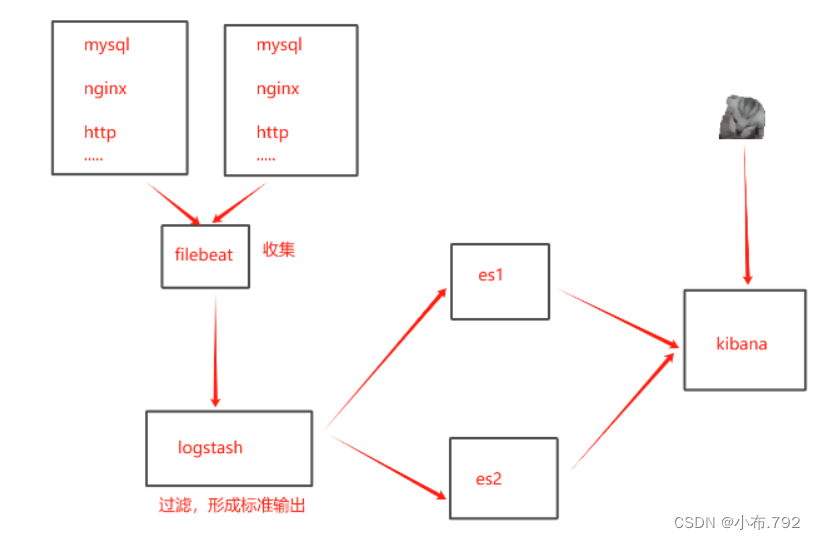
ELK日志收集系统-filbeat
filebeat日志收集工具 elk:filebeat日志收集工具和logstash相同 filebeat是一个轻量级的日志收集工具,所使用的系统资源比logstash部署和启动时使用的资源要小的多 filebeat可以运行在非Java环境,它可以代理logstash在非java环境上收集日志…...
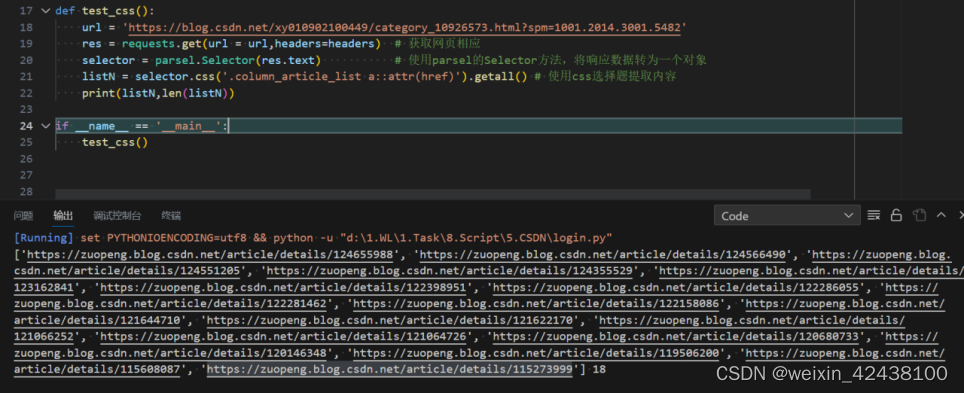
Python小知识
个人学习笔记,用于记录使用过程中好用的技巧、好用的库。 1 小知识 1.1 相对路径 1.2 打包Exe文件 命令: pyinstaller -F main.py其中-F:覆盖之前打包的文件 mian.py:需要打包的Python文件 PS:使用pyinstaller 5.1…...
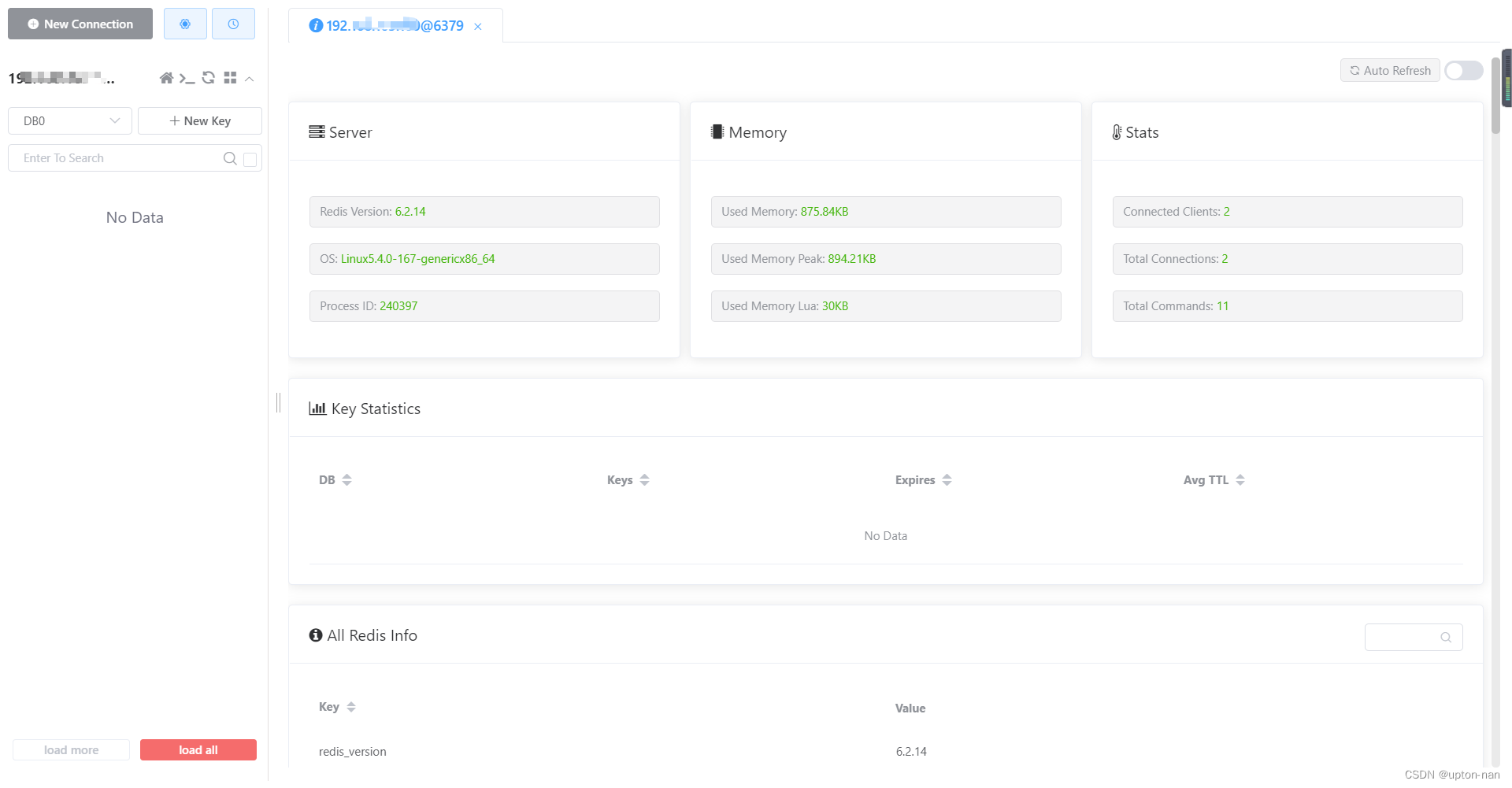
如何在Ubuntu系统上安装Redis
Redis的下载 Redis安装包分为windows版和Linux版当前示例中介绍的是Linux版本Linux的下载地址:Index of /releases/ (redis.io)本次下载的压缩包为:redis-6.2.14.tar.gzRedis的安装 将压缩包通过ssh远程工具上传到Linux服务器中解压压缩包 tar -zxvf red…...
Vue2问题:如何全局使用less和sass变量?
前端功能问题系列文章,点击上方合集↑ 序言 大家好,我是大澈! 本文约2400字,整篇阅读大约需要4分钟。 本文主要内容分三部分,如果您只需要解决问题,请阅读第一、二部分即可。如果您有更多时间ÿ…...
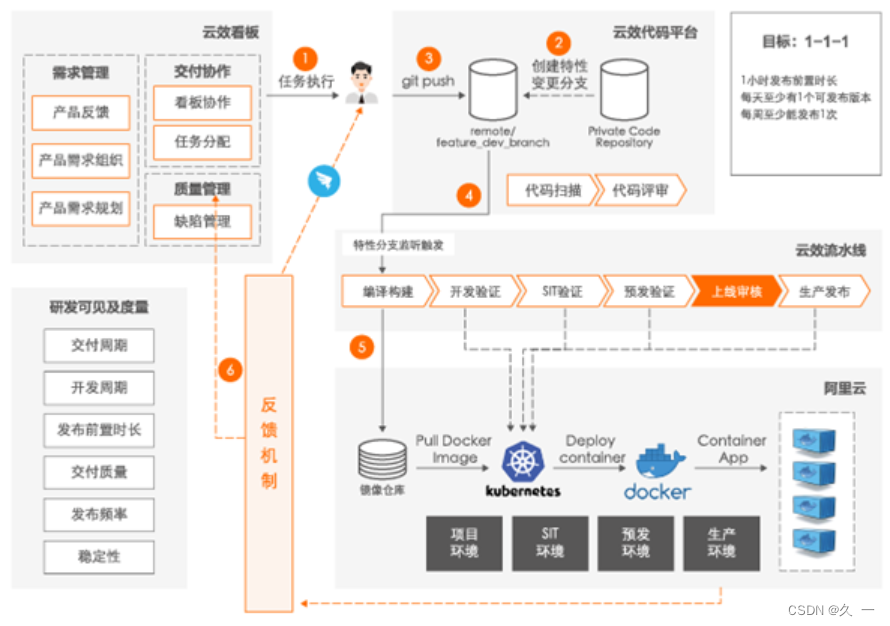
Java 基础学习(四)操作数组、软件开发管理
1 操作数组 1.1.1 System.arraycopy 方法用于数组复制 当需要将一个数组的元素复制到另一个数组中时,可以使用System.arraycopy方法。它提供了一种高效的方式来复制数组的内容,避免了逐个元素赋值的繁琐过程。相对于使用循环逐个元素赋值的方式&#x…...

git仓库如何撤销提交,恢复提交,重置版本命令
撤销提交: 要撤销最近一次提交(未推送到远程仓库),可以使用以下命令: git reset HEAD^该命令将会把最后一次提交的修改从当前主分支中移除,并将这些修改的状态保留在本地工作目录中。 如果想要取消所有的…...
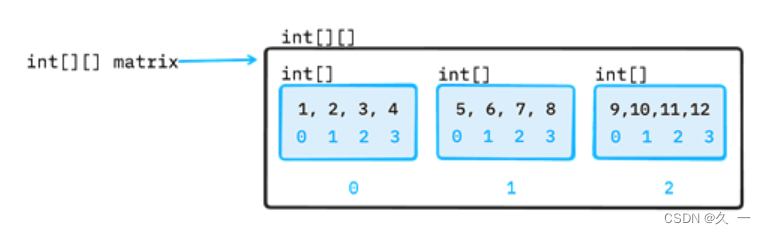
Java 基础学习(三)循环流程控制与数组
1 循环流程控制 1.1 循环流程控制概述 1.1.1 什么是循环流程控制 当一个业务过程需要多次重复执行一个程序单元时,可以使用循环流程控制实现。 Java中包含3种循环结构: 1.2 for循环 1.2.1 for循环基础语法 for循环是最常用的循环流程控制ÿ…...

别太担心,人类只是把一小部分理性和感性放到了AI里
尽管人工智能(AI)在许多方面已经取得了重大进展,但它仍然无法完全复制人类的理性和感性。AI目前主要侧重于处理逻辑和分析任务,而人类则具有更复杂的思维能力和情感经验。 人类已经成功地将一些可以数据化和程序化的理性和感性特征…...
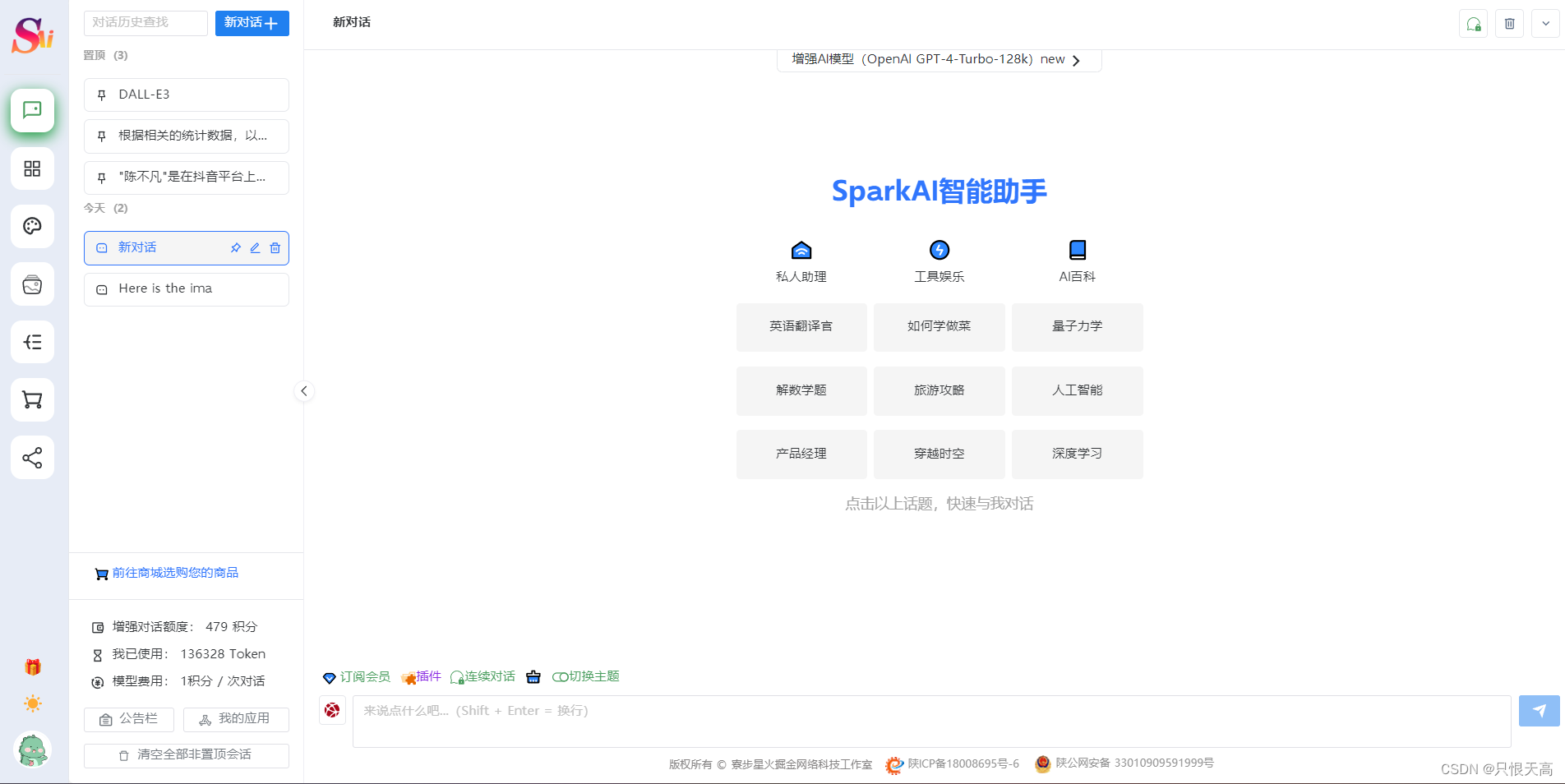
最新AIGC创作系统ChatGPT系统源码+DALL-E3文生图+图片上传对话识图/支持OpenAI-GPT全模型+国内AI全模型
一、AI创作系统 SparkAi创作系统是基于ChatGPT进行开发的Ai智能问答系统和Midjourney绘画系统,支持OpenAI-GPT全模型国内AI全模型。本期针对源码系统整体测试下来非常完美,可以说SparkAi是目前国内一款的ChatGPT对接OpenAI软件系统。那么如何搭建部署AI…...
在centos7上源码安装nginx
1. 安装必要的编译工具和依赖项 在编译Nginx之前,你需要安装一些编译工具和依赖项。可以通过以下命令安装: yum install gcc-c pcre-devel zlib-devel make 2. 下载Nginx源代码 从Nginx官网下载最新的源代码。你可以使用wget命令来下载: …...
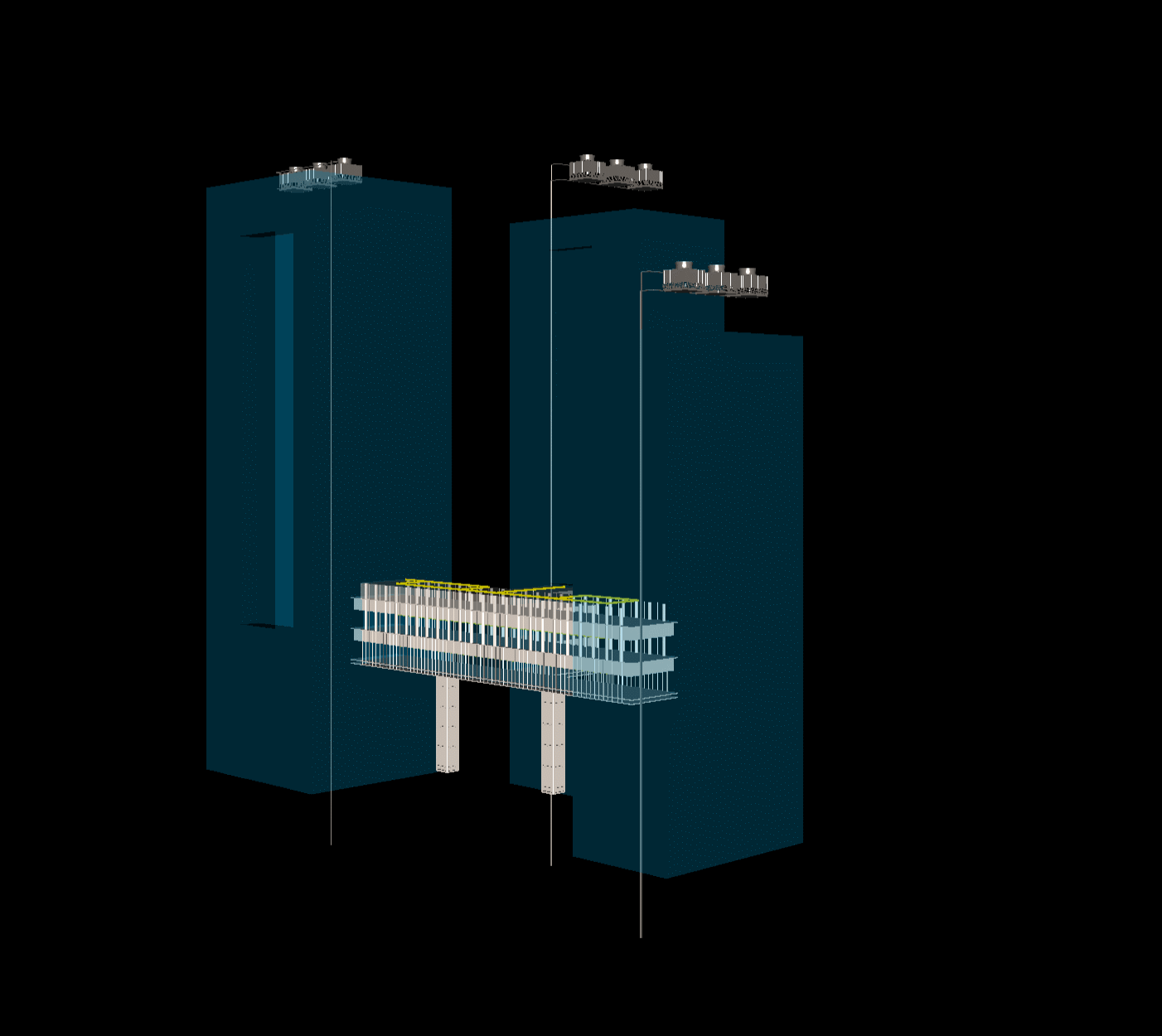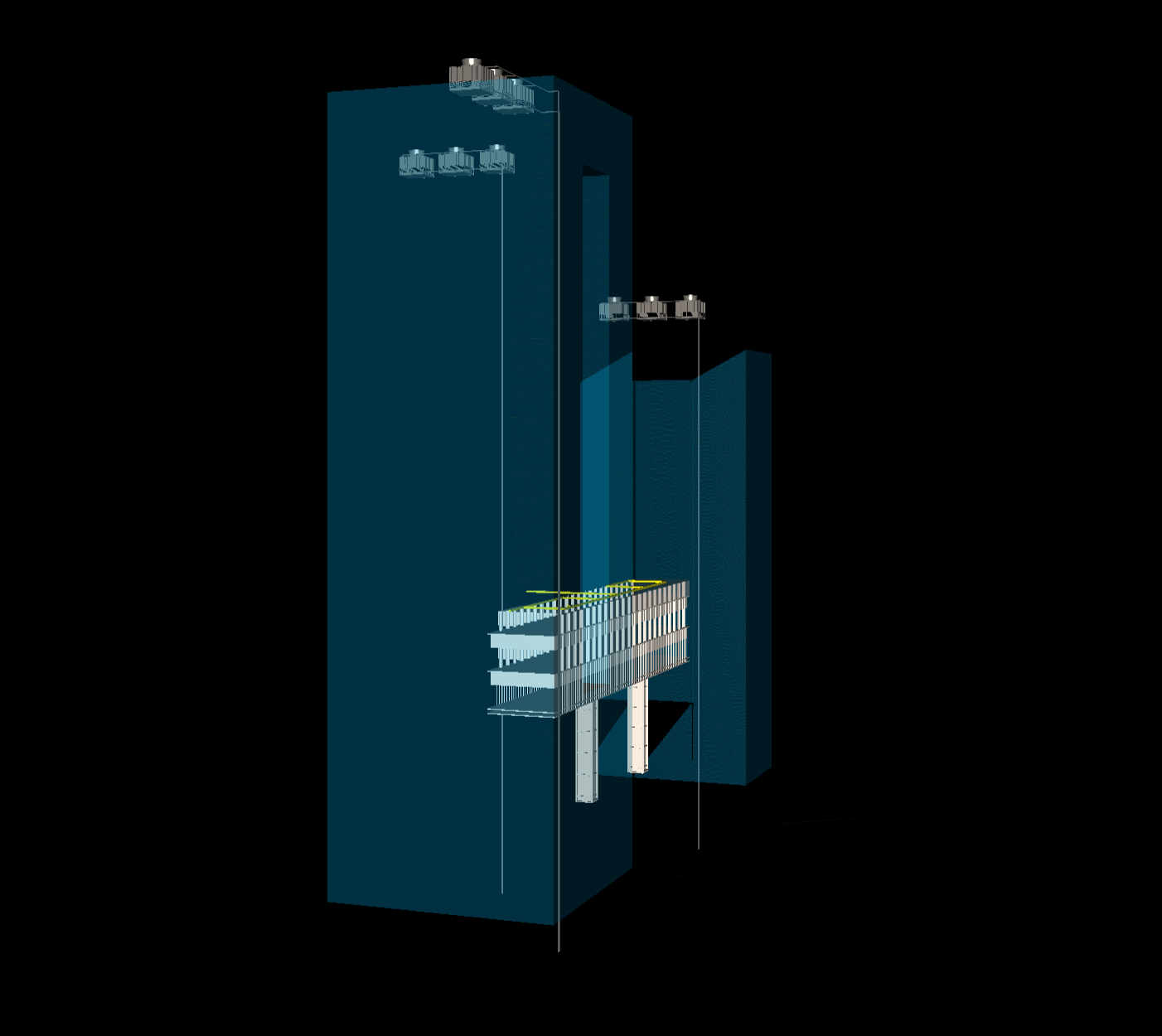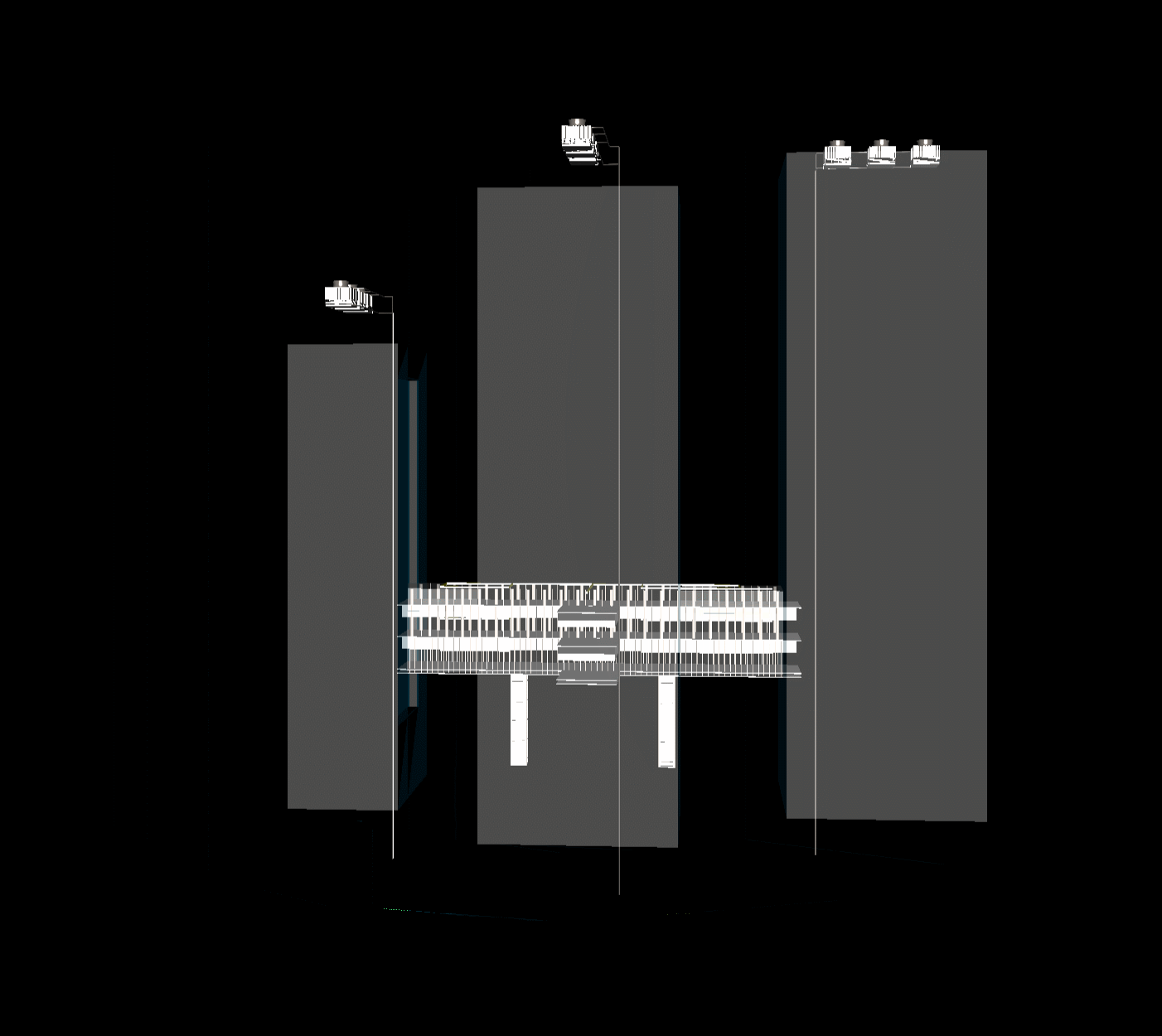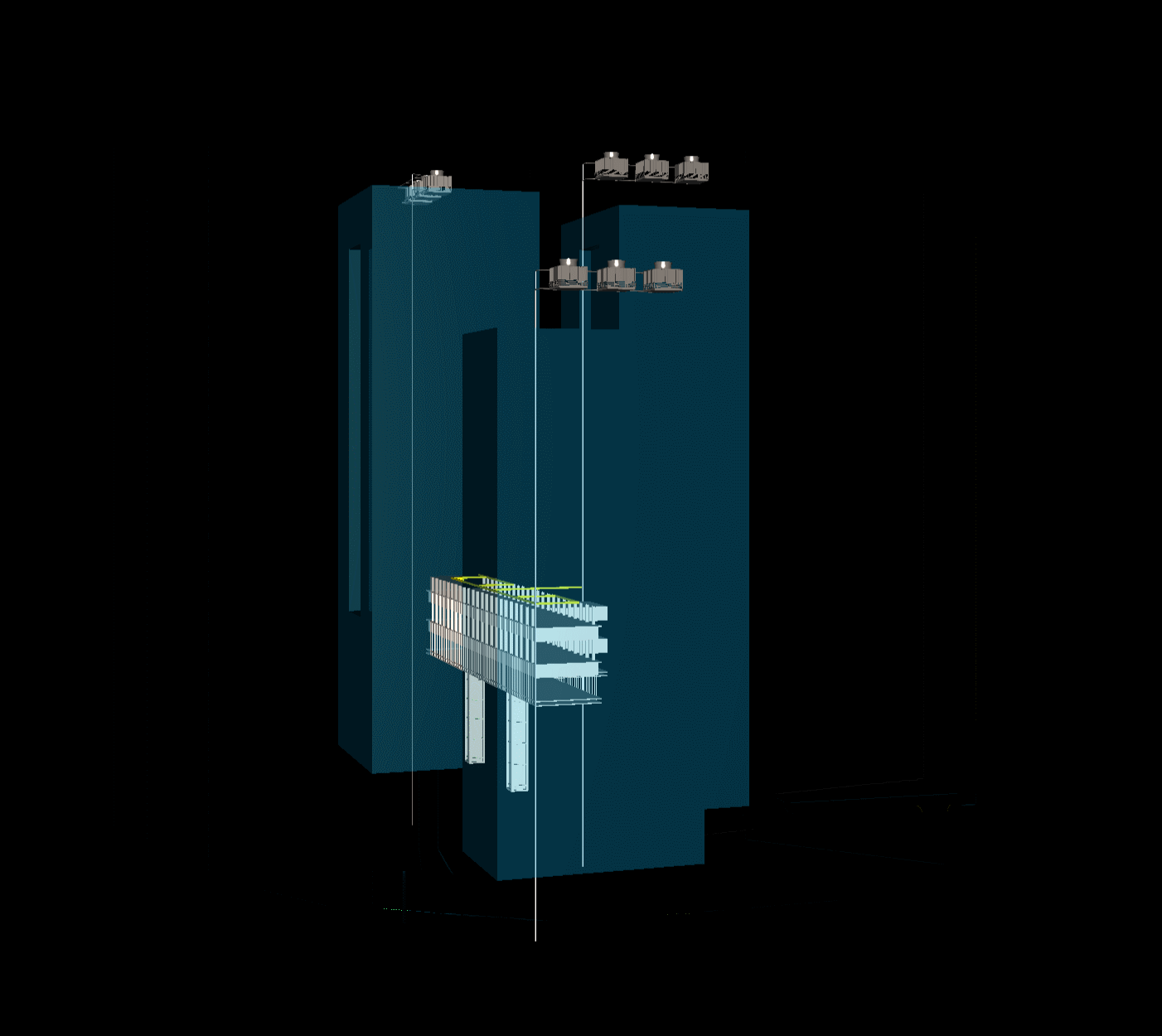
Html网页threejs显示obj,ply三维图像实例
程序示例精选 Html网页threejs显示obj,ply三维图像实例 如需安装运行环境或远程调试,见文章底部个人QQ名片,由专业技术人员远程协助! 前言 这篇博客针对《Html网页threejs显示obj,ply三维图像实例》编写代码,代码整洁࿰…...
Windows平台下的oracle 11G-11.2.0.4补丁升级操作指南
序号 文件名称 文件说明 1 p6880880_112000_MSWIN-x86-64_OPatch 11.2.0.3.33 for DB 11.2.0.0.0 (Feb 2022) 用于升级 OPatch 2 DB_PSU_11.2.0.4.220118 (Jan 2022)_p33488457_112040_MSWIN-x86-64 主要补丁文件 注意:请用管理员权限运行文件内命令&#…...
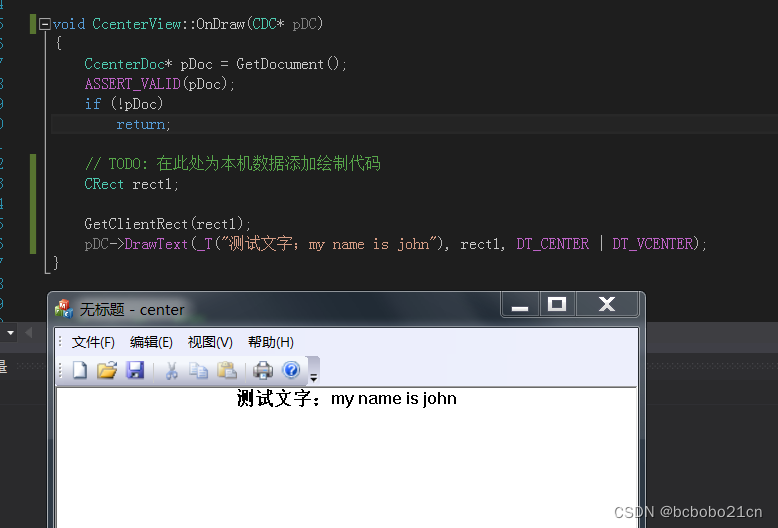
MFC居中显示文字及其应用
首先获取窗口客户区矩形,然后使用DrawText输出,设置DT_CENTER 和 DT_VCENTER标志; 输出如上图;没有实现垂直居中; 最终的代码如下; void CcenterView::OnDraw(CDC* pDC) {CcenterDoc* pDoc = GetDocument();ASSERT_VALID(pDoc);if (!pDoc)return;// TODO: 在此处为…...

50-75GHz大功率六倍频源设计
摘 要 本文介绍了毫米波的特点,根据构成毫米波倍频器的不同器件,介绍了不同毫米波倍频器的实现方法,综述了毫米波倍频器这一领域的研究水平及其发展动态,重点研究频段全波导带宽倍频器的设计方法,从而将波段信号扩展到…...
Qt 软件调试(一) Log日志调试
终于这段时间闲下来了,可以系统的编写Qt软件调试的整个系列。前面零零星星的也有部分输出,但终究没有形成体系。借此机会,做一下系统的总结。慎独、精进~ 日志是有效帮助我们快速定位,找到程序异常点的实用方法。但是好的日志才能…...

docker network容器网络通信
Docker 网络主要有以下两个作用: 容器间的互联和通信以及端口映射容器IP变动时候可以通过服务名直接网络通信而不受到影响 只要是处于同一个Docker 网络下的容器就可以使用服务名直接访问,而无需担心重启。 docker容器网络模式 bridge网络模式&#…...

CVE-2022-4886 ingress命令注入复现与分析
安装 安装ingress-nginx wget https://raw.githubusercontent.com/kubernetes/ingress-nginx/controller-v1.8.4/deploy/static/provider/cloud/deploy.yamlk apply -f deploy.yaml 原理 nginx.ingress.kubernetes.io/rewrite-target标签会在nginx配置进行插入字符串&#…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...
