吴恩达《机器学习》10-6-10-7:学习曲线、决定下一步做什么
一、学习曲线
1. 学习曲线概述
学习曲线将训练集误差和交叉验证集误差作为训练集实例数量(m)的函数绘制而成。这意味着从较少的数据开始,逐渐增加训练集的实例数量。该方法的核心思想在于,当训练较少数据时,模型可能会完美地适应这些数据,但这并不代表它能够很好地适应交叉验证集或测试集数据。

2. 识别高偏差/欠拟合
在学习曲线中,对于高偏差或欠拟合的情况,增加训练集数据可能不会显著改善模型效果。具体而言,如果使用一条直线模型适应数据,无论训练集有多大,模型的误差都可能保持较高,表现出学习曲线趋于平稳。

3. 识别高方差/过拟合
对于高方差或过拟合的情况,学习曲线呈现出一种特殊的模式。当交叉验证集误差远大于训练集误差时,增加更多数据到训练集可能有助于提高算法效果。高方差情况下,模型在训练集上表现很好,但泛化到未见数据时表现不佳。
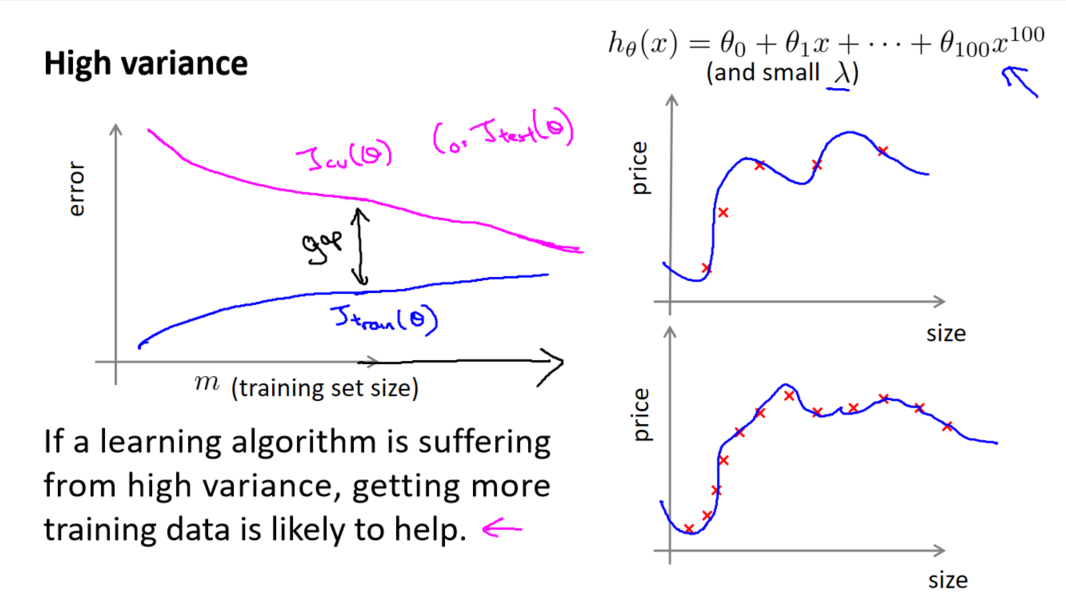
4. 使用学习曲线的价值
学习曲线不仅仅是一种工具,更是算法性能的“合理检验”。通过观察曲线的形状,我们可以快速判断算法的问题所在,是偏差还是方差。这为调整算法提供了重要线索,指导我们如何改进模型的性能。
二、决定下一步做什么
在机器学习中,选择下一步的操作至关重要,而之前学到的诊断法则可以帮助更好地判断应该采取哪些方法来改进学习算法的效果。在这个过程中,可以回顾六种可选的下一步,并根据问题的性质进行选择:
-
获得更多的训练实例 - 解决高方差:如果模型在训练集上表现良好,但在交叉验证集上误差较大,可能是因为训练实例不足导致过拟合。
-
尝试减少特征的数量 - 解决高方差:如果模型复杂度较高,可以考虑减少特征的数量,减轻过拟合问题。
-
尝试获得更多的特征 - 解决高偏差:如果模型欠拟合,可以考虑增加特征数量,提高模型复杂度。
-
尝试增加多项式特征 - 解决高偏差:对于线性模型,可以尝试引入更多的多项式特征,提高模型的灵活性。
-
尝试减少正则化程度 λ - 解决高偏差:如果模型过于正则化,可以减小正则化程度,提高模型对训练数据的拟合度。
-
尝试增加正则化程度 λ - 解决高方差:如果模型过拟合,可以增加正则化程度,限制模型的复杂度。

对于神经网络,调整网络的大小和正则化程度也是一项重要任务。较小的神经网络可能导致高偏差,而较大的神经网络可能导致高方差。通过逐步增加隐藏层的层数,可以使用交叉验证集选择最佳的网络结构。

参考资料:
[中英字幕]吴恩达机器学习系列课程
黄海广博士 - 吴恩达机器学习个人笔记
相关文章:

吴恩达《机器学习》10-6-10-7:学习曲线、决定下一步做什么
一、学习曲线 1. 学习曲线概述 学习曲线将训练集误差和交叉验证集误差作为训练集实例数量(m)的函数绘制而成。这意味着从较少的数据开始,逐渐增加训练集的实例数量。该方法的核心思想在于,当训练较少数据时,模型可能…...
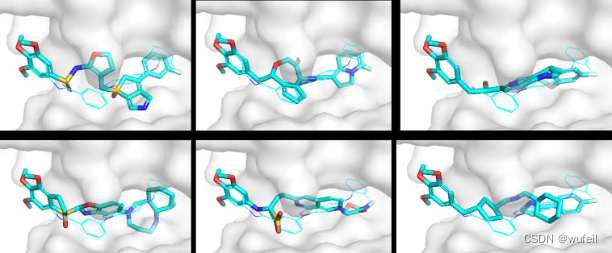
分子骨架跃迁工具-DiffHopp 评测
一、文章背景介绍 DiffHopp模型发表在ICML 2023 Workshop on Computational Biology(简称:2023 ICML-WCB)上的文章。第一作者是剑桥计算机系的Jos Torge。 DiffHopp是一个专门针对骨架跃迁任务而训练的E3等变条件扩散模型。此外,…...

MySQL双主双从数据库集群搭建
1 引言 在之前的文章中提到过相关搭建方法,具体请参考《MySQL主从数据库搭建》这篇文章,本文主要讲述双主双从,双主多从集群的搭建方式。 这里要问一个问题,为什么MySQL要搭建数据库集群呢?我想应该有以下几点原因&…...
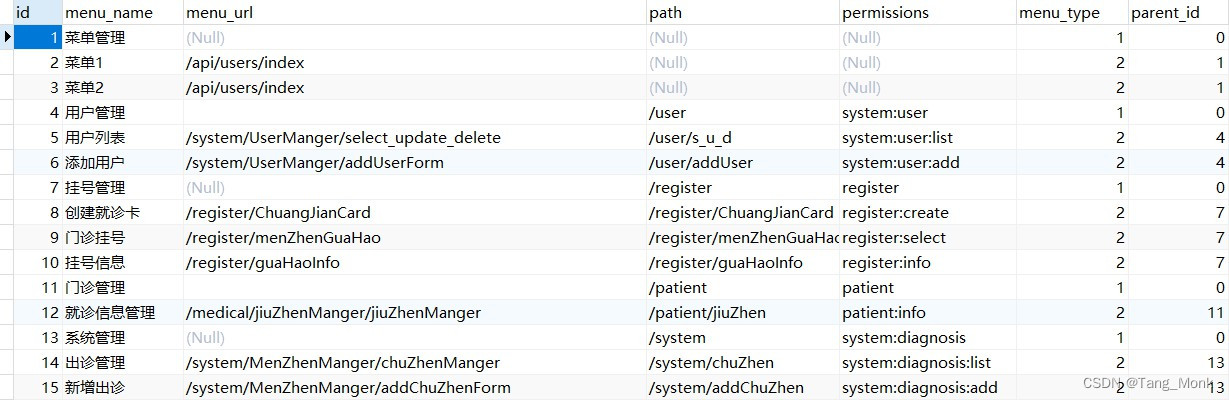
vue实现动态路由菜单!!!
目录 总结一、步骤1.编写静态路由编写router.jsmain.js注册 2.编写permisstions.js权限文件编写permisstions.jsaxios封装的APIstore.js状态库system.js Axios-APIrequest.js axios请求实例封装 3.编写菜单树组件MenuTree.vue 4.主页中使用菜单树组件 总结 递归处理后端响应的…...

企业如何选择安全又快速的大文件传输平台
在现代信息化社会,数据已经成为各个行业的重要资源,而数据的传输和交换则是数据价值的体现。在很多场合,企业需要传输或接收大文件,例如设计图纸、视频素材、软件开发包、数据库备份等。这些文件的大小通常在几百兆字节到几十个字…...
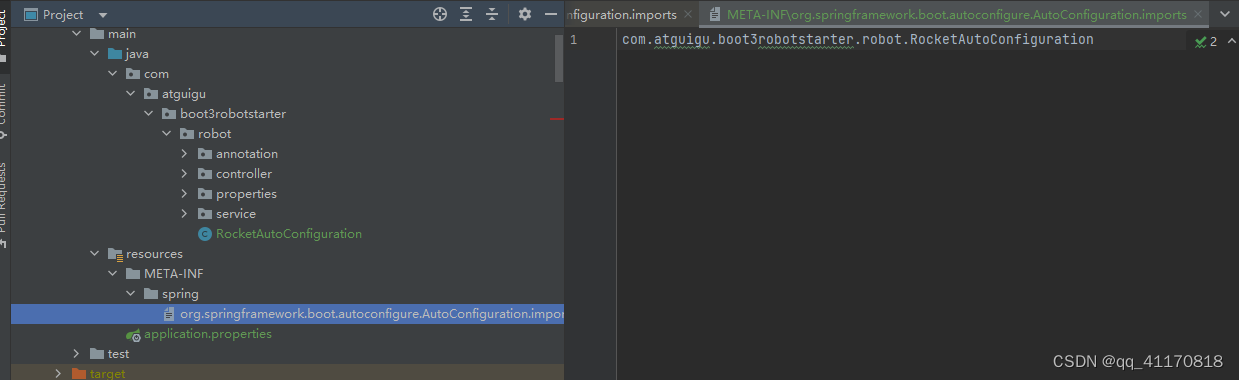
springboot 自定义starter逐级抽取
自定义starter 背景:各个组件需要引入starter 还有自己的配置风格 –基本配置原理 (1)自定义配置文件 导入配置可以在配置文件中自动识别,提示 导入依赖后可以发现提示 (2)配置文件实现 –让配置文件对其他模块生…...

GAN:ImprovedGAN-训练GAN的改进策略
论文:https://arxiv.org/abs/1606.03498 代码:https://github.com/openai/improved_gan 发表:NIPS 2016 一、文章创新 1:Feature matching:特征匹配通过为生成器指定新目标来解决GANs的不稳定性,从而防止…...

docker限制容器内存的方法
在服务器中使用 docker 时,如果不对 docker 的可调用内存进行限制,当 docker 内的程序出现不可预测的问题时,就很有可能因为内存爆炸导致服务器主机的瘫痪。而对 docker 进行限制后,可以将瘫痪范围控制在 docker 内。 因此&#…...

阿里达摩院裁撤量子实验室
我是卢松松,点点上面的头像,欢迎关注我哦! 马云的达摩院也不搞量子计算了,因为缺钱,整体裁掉了达摩院量子实验室,把所有的设备都赠送给了浙江大学。 达摩院量子实验室:总共30个研究员…...

mysql数据库基础知识,Mysql的索引和主键区别,数据库的事务的基本特性
文章目录 数据库基础知识Mysql的索引和主键的区别数据库的事务的基本特性 数据库基础知识 为什么要使用数据库 数据保存在内存 优点: 存取速度快 缺点: 数据不能永久保存 数据保存在文件 优点: 数据永久保存 缺点:1…...

解决Vscode使用git提交卡住的问题
使用Vscode的git提交代码经常会很慢/卡住。 先点击左下角,进入设置 找到git的配置(建议直接搜索),把use Editor As commit input的勾选去掉即可解决。...

Linux C语言 32-网络编程之UDP例程
Linux C语言 32-网络编程之UDP例程 本节关键字:C语言 网络编程 UDP协议 套接字操作 服务端 客户端 相关C库函数:setsockopt, socket, bind, recvfrom, sendto, close 相关接口介绍 Linux C语言 30-套接字操作 例程执行任务说明 本例程中服务端的任务…...
ubuntu22.04系统下载程序和依赖,并拷贝到指定路径下
脚本1 apt install aptitude apt-get -d install xxx #xxx是待下载的安装包 mv /var/cache/apt/archives/* /home/tuners/1apt install aptitude apt-get -d install xxx mv /var/cache/apt/archives/*.deb /home/tuners/1 xxx 为程序包名称 /home/tuners/1为保存程序包的…...
)
Kafka KRaft 版本集群部署详细教程(附配置文件详细解释)
版本说明 Ubuntu 18.04.6Kafka 3.6.0JDK8 集群配置 操作系统ip域名Kafka Broker 端口Kafka Controller 端口Ubuntu 18.04.6192.168.50.131kafka1.com90929093Ubuntu 18.04.6192.168.50.132kafka2.com90929093Ubuntu 18.04.6192.168.50.133kafka3.com90929093 安装 vim, cur…...

在龙蜥 anolis os 23 上 源码安装 PostgreSQL 16.1
在龙蜥 OS 23上,本来想使用二进制安装,结果发现没有针对龙蜥的列表: 于是想到了源码安装,下面我们列出了PG源码安装的步骤: 1.安装准备 1.1.创建操作系统组及用户 groupadd postgres useradd -g postgres -m postgr…...

UDP的不可靠性可以用来做什么
User Datagram Protocol(UDP,用户数据报协议)是互联网协议套件中的一种传输层协议。与TCP不同,UDP是一种无连接的、不可靠的协议。 要知道UDP可以用来做什么,首先我们要知道它有何特点: 1,无连接: UDP是一…...
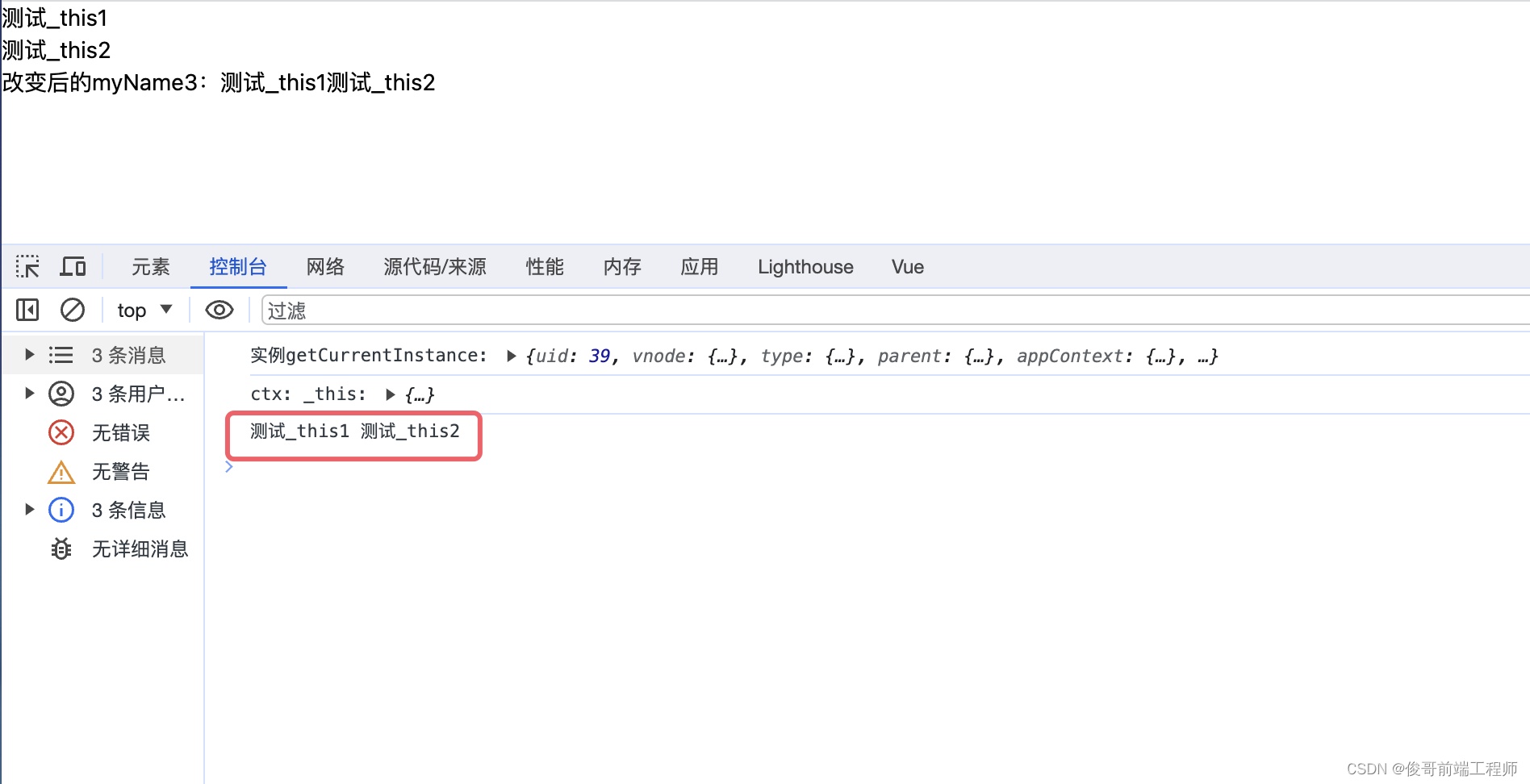
vue3还用this吗?getCurrentInstance获取当前组件实例
在 Vue 2 中,this 关键字代表当前组件实例。在组件的选项对象中,this 可以用于访问组件实例的属性、方法以及 Vue 实例的一些特定方法。 在Vue3中,我们发现this是undefined,那我们真的没法使用this了吗?vu3给我们提供…...

高校学生宿舍公寓报修维修生活管理系统 微信小程序b2529
本课题要求实现一套基于微信小程序宿舍生活管理系统,系统主要包括(管理员,学生、维修员和卫检员)四个模块等功能。 使用基于微信小程序宿舍生活管理系统相对传统宿舍生活管理系统信息管理方式具备很多优点:首先可以大幅…...

C++类与对象(7)—友元、内部类、匿名对象、拷贝对象时编译器优化
目录 一、友元 1、定义 2、友元函数 3、友元类 二、内部类 1、定义 2、特性: 三、匿名对象 四、拷贝对象时的一些编译器优化 1、传值&传引用返回优化对比 2、匿名对象作为函数返回对象 3、接收返回值方式对比 总结: 一、友元 1、定义…...
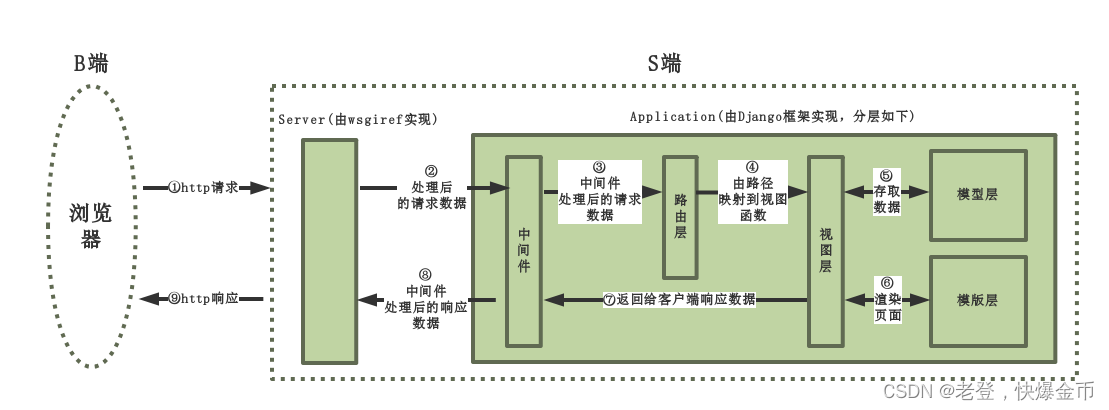
Django回顾2
目录 一.HTTP 1.URL介绍 2.格式: 3.补充: 二.web框架 1.什么是框架 2.什么是web框架 3.wsgi协议 基于wsgi协议的web服务器: 4.协议是怎么规定的 三.Django 1.MVC与MTV模型(所有框架其实都遵循MVC架构) 2.…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...
