C++ day42背包理论基础01 + 滚动数组
背包问题的重中之重是01背包
01背包
有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。
每一件物品其实只有两个状态,取或者不取,所以可以使用回溯法搜索出所有的情况,那么时间复杂度就是o(2^n),这里的n表示物品数量。
所以暴力的解法是指数级别的时间复杂度。进而才需要动态规划的解法来进行优化!
举一个例子:背包最大重量为4,有3个物品,其重量和价值如下表
物品为:
| 重量 | 价值 | |
|---|---|---|
| 物品0 | 1 | 15 |
| 物品1 | 3 | 20 |
| 物品2 | 4 | 30 |
问背包能背的物品最大价值是多少?
动规五部曲
1)确定dp数组以及下标的含义
对于背包问题,有一种写法, 是使用二维数组,即dp[i][j] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少,i代表第几个物品,j代表背包的容量,dp[i][j]代表价值
2)递推公式
对于每一个物品都有放与不放两种状态,所以又有两种情况,取这两种情况的最大值
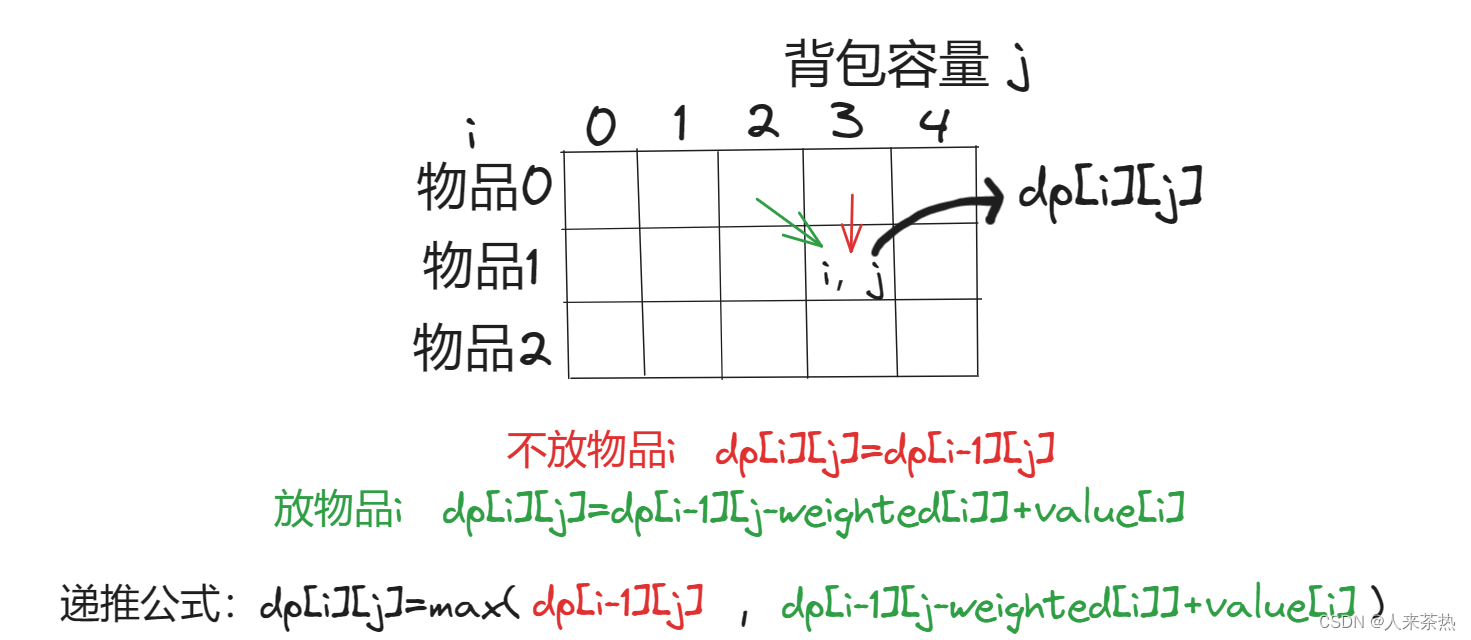
3)dp数组初始化
根据递推公式,可知dp数组是由其左上角和正上方推导而来,所以要对其第一行和第一列进行初始化

其他下标的价值由递推公式更新推导,所以其它地方初始化为任意值均可
4)遍历顺序
因为本题有两个维度,分别为物品维度和背包容量维度,所以到底是先遍历物品呢?还是先遍历背包呢?
可以分类讨论一下
先遍历物品
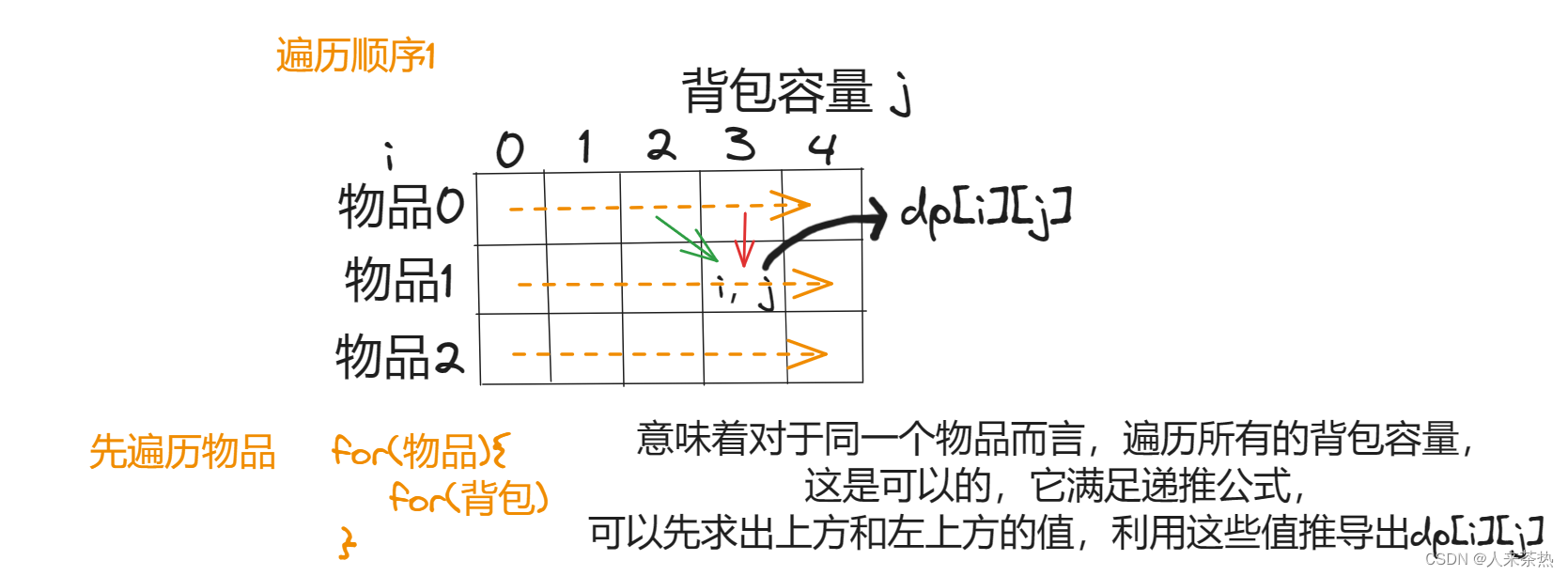
先遍历背包

5)打印dp数组
代码
int weight_bag(vector<int> weight,vector<int> value,int bagweight){vector<vector<int>> dp(weight.size(),vector<int>(bagweight+1,0));//初始化.对于物品0for(int j=weight[0];j<=bagweight;j++){dp[0][j]=value[0];}//递推(先遍历物品,再遍历背包)for(int i=1;i<weight.size();i++){for(int j=0;j<=bagweight;j++){if(j<weight[i]) dp[i][j]=dp[i-1][j];//如果当前物品重量比背包容量大,则装不下该物品//如果当前物品重量比背包容量小,那么可以有两种选择,装下该物品,或是不装该物品else dp[i][j]=max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i]);}}return dp[weight.size()-1][bagweight];
}01背包(滚动数组)
把dp[i - 1]这一层拷贝到dp[i]上,只用一个一维数组dp[j],可以理解是一个滚动数组。
滚动数组需要满足的条件是上一层可以重复利用,直接拷贝到当前层,一直处于一种刷新的状态
动规五部曲
1)确定dp数组的定义
在一维dp数组中,dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j]。
2)一维dp数组的递推公式
dp[j]有两个选择,一个是不放物品i,取自己dp[j] 相当于 二维dp数组中的dp[i-1][j];一个是放物品i,取dp[j - weight[i]] + value[i],取二者当中的最大值
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);3)一维dp数组的初始化
dp[0]就应该是0,因为背包容量为0所背的物品的最大价值就是0。
除了下标0的位置,初始为0,其他下标应该初始化多少呢?
根据递推公式,dp数组在推导的时候一定是取价值最大的数,那么非0下标都初始化为0就可以了,这样才能让dp数组在递归公式的过程中取的最大的价值,而不是被初始值覆盖了。
4)一维dp数组的遍历顺序
一维dp遍历的时候,背包是从大到小,注意一定要是倒序遍历
倒序遍历是为了保证物品i只被放入一次!。但如果一旦正序遍历了,那么物品0就会被重复加入多次!
因为根据递推公式,每个物品只放一次,在遍历物品的时候,变动j时,每次都要刷新dp[j]
dp[1]=dp[1-weight[0]]+value[0]=dp[0]+15=0+15=15
dp[2]=dp[2-weight[0]]+value[0]=dp[1]+value[0]=15+15=30,这里物品0会放入两次,因为前面刷新了dp[1],初始值会被修改,连带着后面的dp[2]会受到波及!!!!
为什么二维dp数组遍历的时候不用倒序呢?
因为对于二维dp,dp[i][j]都是通过上一层即dp[i - 1][j]计算而来,本层的dp[i][j]并不会被覆盖!,因为是二维数组,没有动态刷新,所以一旦求出数值,便会一直在那保持不变
两个嵌套for循环的顺序,代码中是先遍历物品嵌套遍历背包容量,那可不可以先遍历背包容量嵌套遍历物品呢?
不可以!因为一维dp的写法,背包容量一定是要倒序遍历(原因上面已经写了),如果遍历背包容量放在上一层,那么每个dp[j]就只会放入一个物品,即:背包里只放入了一个物品。
因为是每次只对一个背包容量进行求解,
dp[4]=dp[4-1]+value[0]=15
dp[4]=max(15,dp[4-3]+value[1])=max(15,20)=20
dp[4]=max(10,dp[4-4]+value(2))=max(20,30)=30
dp[3]=dp[3-1]+value(0)=value(0)=15
........
如上,因为是倒序遍历和初始化的存在,针对每个背包容量,每次都只放进了一个物品,不能将两个或多个物品的情况考虑在内
dp[4]=dp[4-1]+value[0]=15
dp[3]=max(dp[3],dp[3-1]+value[0])=15
dp[2]=max(dp[2],dp[2-1]+value[0])=15
dp[1]=max(dp[1],dp[1-1]+value[0])=15
dp[4]=max(dp[4],dp[4-3]+value[1])=max(15,15+20)=35
.........
如上,每个背包的容量随着物品的变动与前面每一个物品的情况结合起来,这才是正解
倒序遍历的原因是,本质上还是一个对二维数组的遍历,并且右下角的值依赖上一层左上角的值,因此需要保证左边的值仍然是上一层的,从右向左覆盖。
倾向于使用一维dp数组的写法,比较直观简洁,而且空间复杂度还降了一个数量级!
代码
int weightvalue(int bagweight,vector<int>weight,vector<int>value){//初始化dp数组vector<int> dp(bagweight+1,0);//递推for(int i=0;i<weight.size();i++){for(int j=bagweight;j>=weight[i];j--){dp[j]=max(dp[j],dp[j-weight[i]]+value[i]);}}return dp[bagweight];
}背包问题应用1
题目:416分割等和子集
题目链接:分割等和子集
对题目的理解
非空数组由正整数组成,是否可以将这个数组分割成两个子集,使得两个子集的元素和相等
将问题具象化:只要找到集合里能够出现 sum / 2 的子集总和,就算是可以分割成两个相同元素和子集了。
集合中的元素只能使用一次,因此使用的是01背包
只有确定了如下四点,才能把01背包问题套到本题上来。
- 背包的容量为sum / 2
- 背包要放入的商品(集合里的元素)重量为nums[i],价值也为nums[i]
- 背包如果正好装满,说明找到了总和为 sum / 2 的子集。
- 背包中每一个元素是不可重复放入
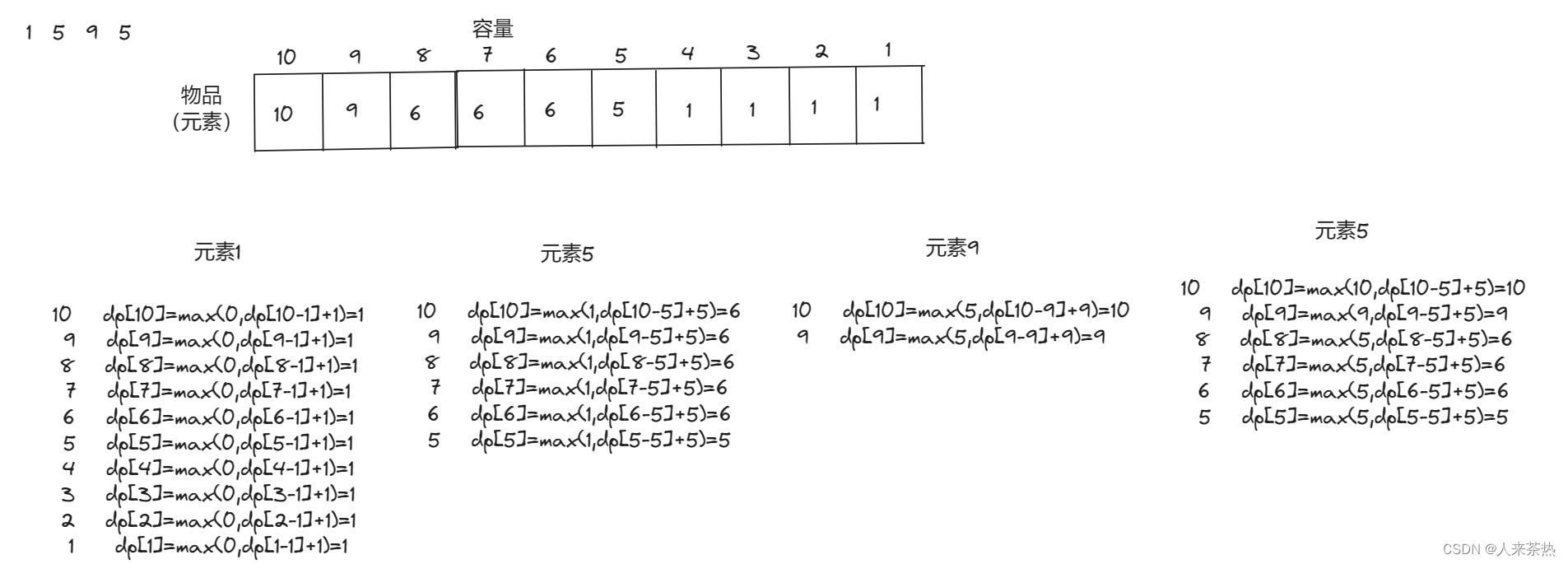
动规五部曲
1)确定dp数组含义及下标
dp[j]:容量为j的背包所背的最大价值为dp[j]
集合中的每个元素既是重量也是价值 dp[target]==target 背包装满 其中target=sum/2
2)递推公式
背包的递推公式:dp[j]=max(dp[j],dp[j-weight[i]]+value[i])
所以本题的递推公式:dp[j]=max(dp[j],dp[j-nums[i]]+nums[i])
3)dp数组初始化
dp[0]=0 ,非零下标进行初始化,dp[i]=0,根据递推公式,不能初始化别的值,初始化为非负整数的最小值,即0,这样才能让dp数组在递推的过程中取得最大的价值,而不是被初始值覆盖了。
4)遍历顺序
遍历顺序:先正序遍历物品,后倒序遍历背包容量
for(i=0;i<nums.size(i++)){
for(j=target;j>=nums[i];j--)}
5)打印dp数组
代码
class Solution {
public:bool canPartition(vector<int>& nums) {vector<int> dp(10001,0);//定义dp数组,并将其初始化为0,因为数组中的元素最大是100,且至少有200个数那么最大的重量为200*100=20000,背包中只有一半容量就可以了int sum = 0;for(int i=0;i<nums.size();i++){sum += nums[i];}if(sum % 2==1) return false;//如果和的一半是奇数,那么不可能有两个子集和相等int target = sum/2;//递推公式//先正序遍历物品,后倒序遍历背包for(int i=0;i<nums.size();i++){for(int j=target;j>=nums[i];j--){dp[j]=max(dp[j],dp[j-nums[i]]+nums[i]);}}if(dp[target]==target) return true;return false;}
};- 时间复杂度:O(n^2)
- 空间复杂度:O(n),虽然dp数组大小为一个常数,但是大常数
相关文章:

C++ day42背包理论基础01 + 滚动数组
背包问题的重中之重是01背包 01背包 有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。 每一件物品其实只有两个状态,取或者不…...

数字人透明屏幕是如何工作的?
数字人透明屏幕是一种令人兴奋的科技产品,它结合了人脸识别、全息影像技术以及透明屏幕,为人们带来了全新的互动体验。本文将详细介绍数字人透明屏幕的工作原理以及其应用场景。 工作原理 数字人透明屏幕的工作原理主要包括人脸识别和全息影像技术。人脸…...

MIGO收货报替代“ZF002“, 步骤““ 中存在语法错误消息号 GB032错误
MIGO收货报替代"ZF002", 步骤"" 中存在语法错误消息号 GB032错误。替代"ZF002", 步骤"" 中存在语法错误消息号 GB032诊断 在 ABAP 代码生成过程中,在替代ZF002中发现了语法错误。 系统响应 未为该布尔陈述生成 ABAP 代码&…...
Vue3的transition标签以及animate.css使用详解
一:前言 在项目开发中,有一种特殊情况是使用动画过渡去完成某个效果。比如淡入淡出,或者在动画完成后执行某些操作等。在以前开发中我们通常会选择使用 CSS3 进行研发。但是这样会有很多不好的地方,比如最原始化的封装,…...

IDEA不支持Java8了怎么办?
IDEA不支持Java8了怎么办? 01 异常发生场景 当我准备创建一个springboot项目时,发现Java8没了 02 问题的产生及其原因 查阅了官方文档之后,确认了是Spring Boot 不再支持 Java 8,不是我的问题,这一天终于还是来了 0…...
)
flutter的TextField参数、案例整理(上)
TextField 概述 TextField 用于文本输入 构造函数 const TextField({Key key,this.controller, this.focusNode,this.decoration const InputDecoration(),TextInputType keyboardType,this.textInputAction,this.textCapitalization TextCapitalization.none,this.style…...

【Linux进阶之路】进程间通信
文章目录 一、原理二、方式1.管道1.1匿名管道1.1.1通信原理1.1.2接口使用 1.2命名管道 2.共享内存2.1原理2.2接口使用 3.消息队列原理 4.信号量引入原理 总结 一、原理 进程间的通信是什么?解释: 简单理解就是,不同进程之间进行数据的输入输出…...
深度学习框架配置
目录 1. 配置cuda环境 1.1. 安装cuda和cudnn 1.1.1. 显卡驱动配置 1.1.2. 下载安装cuda 1.1.3. 下载cudnn,将解压后文件复制到cuda目录下 1.2. 验证是否安装成功 2. 配置conda环境 2.1. 安装anaconda 2.2. conda换源 2.3. 创建conda环境 2.4. pip换源 3.…...

全局配置
1.全局配置文件及其配置项 1.1.小程序窗口 1.2 窗口节点 1.2.1 导航栏标题 标题: 标题颜色: 背景色:只支持16进制值 下拉刷新: 刷新背景色: 刷新样式: 触底距离:...

leetcode算法之字符串
目录 1.最长公共前缀2.最长回文子串3.二进制求和4.字符串相乘 1.最长公共前缀 最长公共前缀 class Solution { public:string longestCommonPrefix(vector<string>& strs) {//法一:两两比较string ret strs[0];for(int i1;i<strs.size();i){ret f…...

mongodb查询数据库集合的基础命令
基础命令 启动mongo服务 mongod -f /usr/local/mongodb/mongod.conf //注意配置文件路径停止mongo服务 关闭mongodb有三种方式: 一种是进入mongo后通过mongo的函数关闭; use admin db.shutdownServer()一种是通过mongod关闭; mongod --s…...
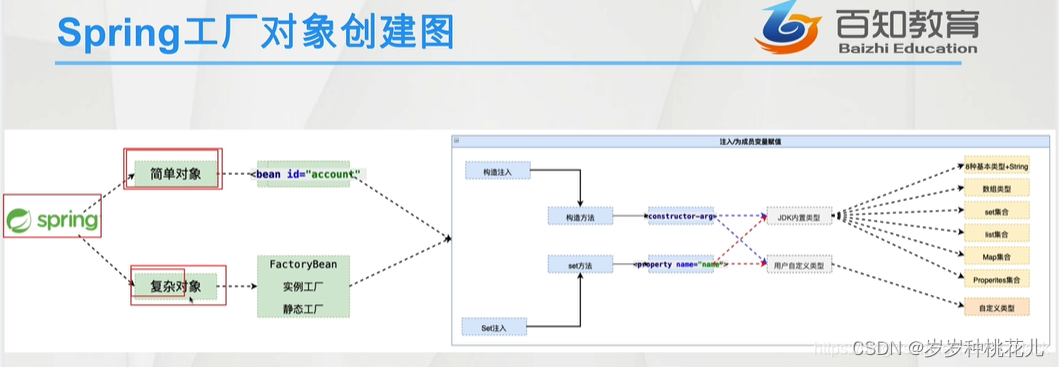
基于FactoryBean、实例工厂、静态工厂创建Spring中的复杂对象
😉😉 学习交流群: ✅✅1:这是孙哥suns给大家的福利! ✨✨2:我们免费分享Netty、Dubbo、k8s、Mybatis、Spring...应用和源码级别的视频资料 🥭🥭3:QQ群:583783…...
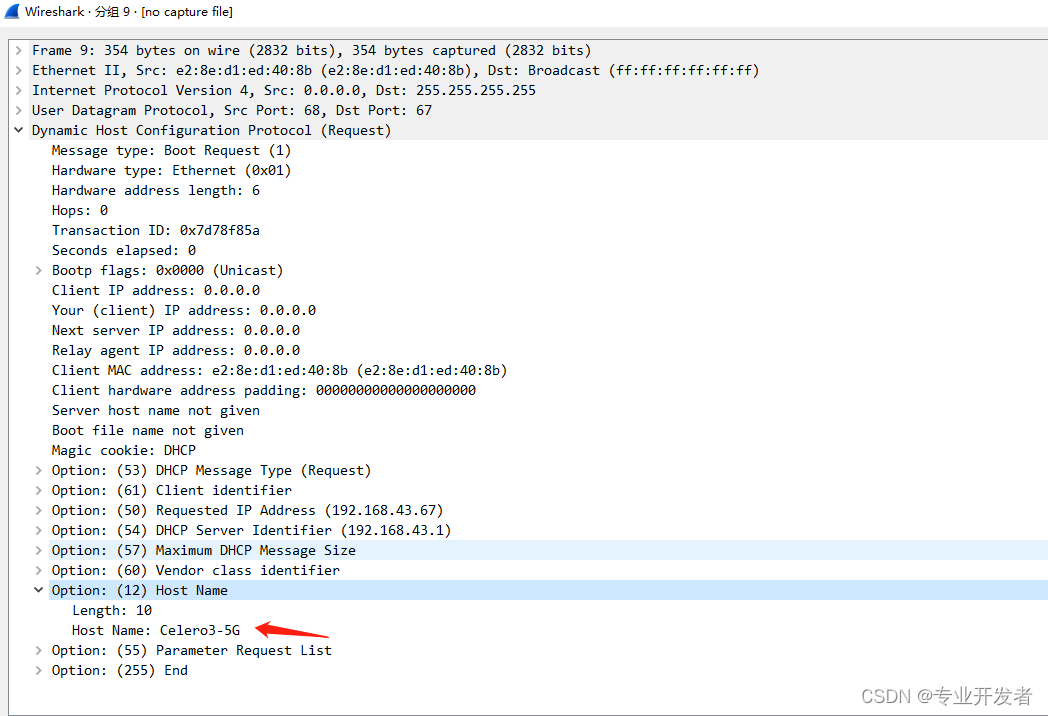
Android 如何让路由器或者其他AP设备获取到主机名
问题原因: 连接到AP设备后,发现主机名在路由器或者其他AP设备都无法正常显示 抓取tcpdump log发现DHCP request option中没有携带host name(Option 12)字段 如下图所示 修改方法: 将config_dhcp_client_hostname配置true后,可以看到host name了 具体代码逻辑如下 pack…...
java三大集合类--List
List Set Map 一、List 几个小问题: 1、接口可以被继承吗?(可以) 2、接口可以被多个类实现吗?(可以) 3、以下两种写法有什么区别? //List list1new List();是错误的因为List()…...

机器人向前冲
欢迎来到程序小院 机器人向前冲 玩法:一直走动的机器人,点击鼠标左键进行跳跃,跳过不同的匝道,掉下去即为游戏接续, 碰到匝道铁钉游戏结束,一直往前冲吧^^。开始游戏https://www.ormcc.com/play/gameStart…...

jq——实现弹幕滚动(往左滚动+往右滚动)——基础积累
最近同事在写弹幕功能,下面记录以下代码: 1.html代码 <div id"scrollContainer"></div>2.引入jq <script src"./script/jquery-1.8.3.js" type"text/javascript"></script>3.jq代码——往左滚…...
深度学习第2天:RNN循环神经网络
☁️主页 Nowl 🔥专栏《机器学习实战》 《机器学习》 📑君子坐而论道,少年起而行之 文章目录 介绍 记忆功能对比展现 任务描述 导入库 处理数据 前馈神经网络 循环神经网络 编译与训练模型 模型预测 可能的问题 梯度消失 梯…...

深度学习之基于百度飞桨PaddleOCR图像字符检测识别系统
欢迎大家点赞、收藏、关注、评论啦 ,由于篇幅有限,只展示了部分核心代码。 文章目录 一项目简介主要特点使用步骤 二、功能三、系统四. 总结 一项目简介 # Introduction to PaddleOCR Image Character Detection and Recognition System Based on Baidu…...

九、LuaTable(表)
文章目录 一、定义二、Table(表)的构造三、Table 操作(一)Table连接(二)插入和移除(三)Table 排序(四)Table 最大值 一、定义 table 是 Lua 的一种数据结构用来帮助我们创建不同的数…...
每日一题(LeetCode)----链表--链表最大孪生和
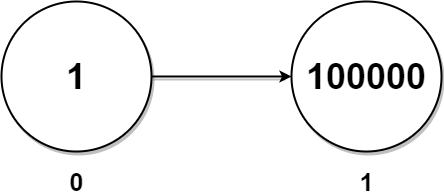
每日一题(LeetCode)----链表–链表最大孪生和 1.题目(2130. 链表最大孪生和) 在一个大小为 n 且 n 为 偶数 的链表中,对于 0 < i < (n / 2) - 1 的 i ,第 i 个节点(下标从 0 开始)的孪生节点为第 (n…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

针对药品仓库的效期管理问题,如何利用WMS系统“破局”
案例: 某医药分销企业,主要经营各类药品的批发与零售。由于药品的特殊性,效期管理至关重要,但该企业一直面临效期问题的困扰。在未使用WMS系统之前,其药品入库、存储、出库等环节的效期管理主要依赖人工记录与检查。库…...

MeshGPT 笔记
[2311.15475] MeshGPT: Generating Triangle Meshes with Decoder-Only Transformers https://library.scholarcy.com/try 真正意义上的AI生成三维模型MESHGPT来袭!_哔哩哔哩_bilibili GitHub - lucidrains/meshgpt-pytorch: Implementation of MeshGPT, SOTA Me…...
Element-Plus:popconfirm与tooltip一起使用不生效?
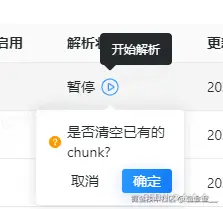
你们好,我是金金金。 场景 我正在使用Element-plus组件库当中的el-popconfirm和el-tooltip,产品要求是两个需要结合一起使用,也就是鼠标悬浮上去有提示文字,并且点击之后需要出现气泡确认框 代码 <el-popconfirm title"是…...
