PowerShell命令小记
1. 使用命令删除指定文件或文件夹
- 在 PowerShell 中,你可以使用
Remove-Item命令递归删除文件夹下的指定文件。以下是一条命令的示例,该命令删除指定文件夹及其子文件夹中的所有 .txt 文件:
Remove-Item -Path "D:\test" -Recurse -Filter *.txt
请将 D:\test 替换为你要删除文件的文件夹路径,将*.txt替换为你想删除的文件的筛选条件。这个命令将删除指定文件夹及其子文件夹中的所有匹配条件的文件。确保在使用此命令时小心,因为删除操作是不可逆的。
- 如果你想在 PowerShell 中一条命令递归删除多个文件夹下的指定文件夹及其内部的所有文件和子文件夹,可以使用
Remove-Item命令结合ForEach-Object来处理多个文件夹。以下是一条示例命令:
Get-ChildItem -Path "C:\Path\To\Your\Folders" -Directory | ForEach-Object { Remove-Item -Path $_.FullName -Recurse }
请将 C:\Path\To\Your\Folders替换为包含多个文件夹的父文件夹路径。这个命令将获取指定路径下的所有子文件夹,并对每个子文件夹应用 Remove-Item -Recurse,以递归删除其内部的所有文件和子文件夹。确保在使用此命令时小心,因为删除操作是不可逆的。请谨慎操作,确保你要删除的内容是正确的。
- 删除当前目录及其子目录中所有名为
node_modules的文件夹,然后删除这些文件夹及其内部的所有内容。
# Get-ChildItem * -Include node_modules -Recurse:获取当前目录及其子目录中所有包含名为 node_modules 的文件夹。-Recurse 参数表示要递归搜索子目录。
# |(管道符号):将上一个命令的输出传递给下一个命令。
# Remove-Item:删除传递给它的对象。在这个情况下,它删除了 Get-ChildItem 返回的所有文件夹。Get-ChildItem * -Include node_modules -Recurse | Remove-Item
上面操作会递归每一个文件,每个文件都需要进行确认操作,神烦!!! 在这个命令中,-Force 参数被添加到 Remove-Item 命令中,用于强制删除文件或文件夹而无需确认。这样可以加快删除过程,但请谨慎使用,因为删除操作是不可逆的。
Get-ChildItem * -Include node_modules -Recurse | Remove-Item -Force -Recurse
相关文章:

PowerShell命令小记
1. 使用命令删除指定文件或文件夹 在 PowerShell 中,你可以使用 Remove-Item 命令递归删除文件夹下的指定文件。以下是一条命令的示例,该命令删除指定文件夹及其子文件夹中的所有 .txt 文件: Remove-Item -Path "D:\test" -Recur…...

C语言小练
目录 打印斐波那契数列指定位置的值 给定两个数,求这两个数的最大公约数 三个数从大到小输出 模拟用户登陆情况,且只能输如三次 采用二分法查找数组中的指定元素 打印输出九九乘法表 数一下1-100中所有整数出现多少个数字9 打印1-200之间的素数&…...
Webhook端口中的自签名身份验证
概述 有时,可能需要通过 Webhook 端口从交易伙伴处接收数据,但该交易伙伴可能需要更多的安全性,而不仅仅是用于验证入站 Webhook 请求的基本身份验证用户名/密码 – 或者您可能只想在入站 Webhook 消息上添加额外的安全层。 使用 Webhook 端…...
:变量、嵌套规则和混合器等高级功能)
CSS预处理器(如Sass或Less):变量、嵌套规则和混合器等高级功能
在Vue项目中,可以使用CSS预处理器(如Sass或Less)来编写样式。 这些预处理器提供了一些高级功能,如变量、嵌套规则和混合器等。 1. 变量 在Sass中,我们可以使用$符号定义变量。这些变量方便我们在多个地方重复使用&a…...

【Linux】Linux第一个小程序 --- 进度条
👦个人主页:Weraphael ✍🏻作者简介:目前正在学习c和Linux还有算法 ✈️专栏:Linux 🐋 希望大家多多支持,咱一起进步!😁 如果文章有啥瑕疵,希望大佬指点一二 …...

每日一练:约瑟夫生者死者小游戏
1. 问题描述 约瑟夫问题(Josephus problem)是一个经典的数学和计算机科学问题,源于犹太历史学家弗拉维奥约瑟夫斯(Flavius Josephus)的著作《犹太战记》。问题的描述如下: 在这个问题中,有n…...

双指针算法(题目与答案讲解)
文章目录 题目移动零复写零两数之和N数之和(>2个数) 答案讲解移动零复写零两数之和N数之和 题目 力扣 移动零 1、移动零:题目链接 复写零 2、复写零:题目链接 两数之和 3、两数之和题目链接 N数之和(>2个数) 4、N数之和(三个数、四个数) 三个数:题目链接 四个数题目链接…...
python服装电商系统vue购物商城django-pycharm毕业设计项目推荐
系统面向的使用群体为商家和消费者,商家和消费者所承担的功能各不相同,所对象的权限也各不相同。对于消费者和商家设计的功能如下: 对于消费者设计了五大功能模块: (1) 商品信息:用户可在商品…...
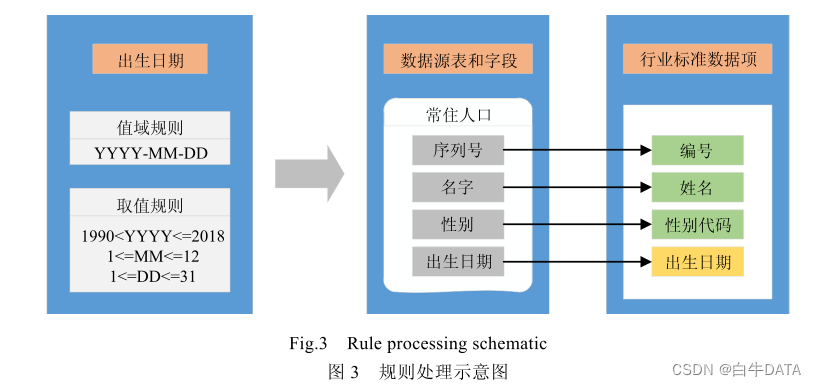
数据治理技术:研究现状与数据规范
随着信息技术的迅速发展,数据规模逐渐扩大,与此同时,劣质数据也随之而来,极大地降低了数据挖掘的质量,对信息社会造成了严重的困扰,劣质数据大量存在于很多领域和机构,国外权威机构的统计表明:美…...
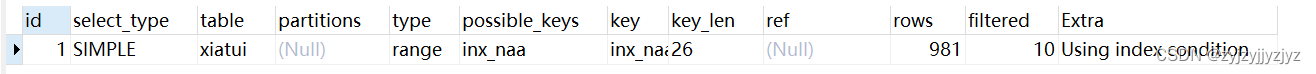
一文彻底理解索引下推
了解索引下推吗?二级索引取出的数据是依次回表还是一次回表?索引下推是为了什么发明的? 看完这个文章你将知道上面的问题。 索引下推的概念 从MySQL5.6开始引入的一个特性,索引下推通过减少回表的次数来提高数据库的查询效率; 注意&#…...
Springboot3+vue3从0到1开发实战项目(一)
一. 可以在本项目里面自由发挥拓展 二. 知识整合项目使用到的技术 后端开发 : Validation, Mybatis,Redis, Junit,SpringBoot3 ,mysql,Swagger, JDK17 ,JWT,项目部署 前端开发: Vue3,Vite&am…...

[字符串操作] 有年代的病历单
有年代的病历单 题目描述 小英是药学专业大三的学生,暑假期间获得了去医院药房实习的机会。 在药房实习期间,小英扎实的专业基础获得了医生的一致好评,得知小英在计算概论中取得过好成绩后,主任又额外交给她一项任务,…...
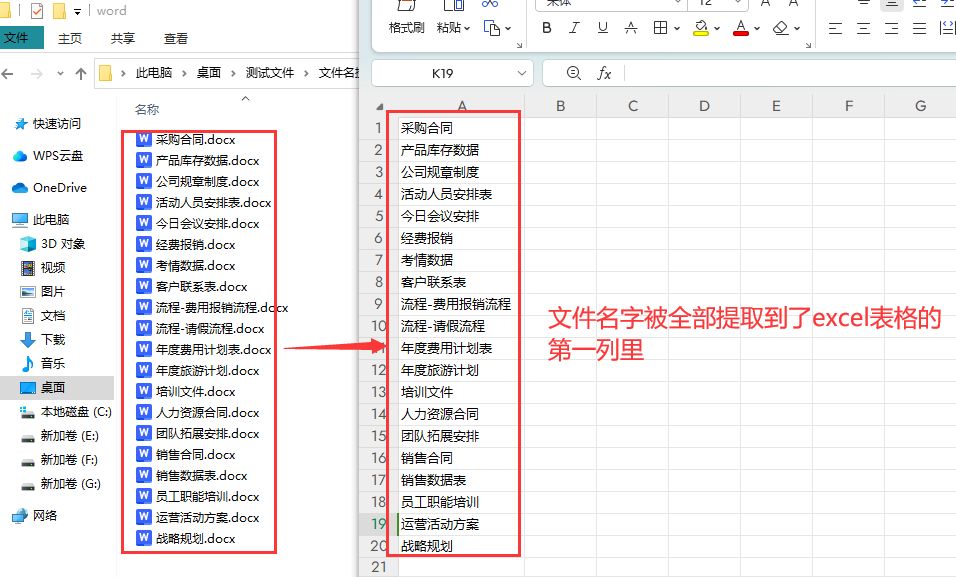
怎么批量提取文件名字到Excel中?
怎么批量提取文件名字到Excel中?Excel是由微软公司开发的一种电子表格软件,它是Microsoft Office办公套件的一部分。Excel提供了强大的数据处理和分析功能,用户可以使用Excel创建、编辑和管理电子表格,进行各种计算、数据分析、图…...
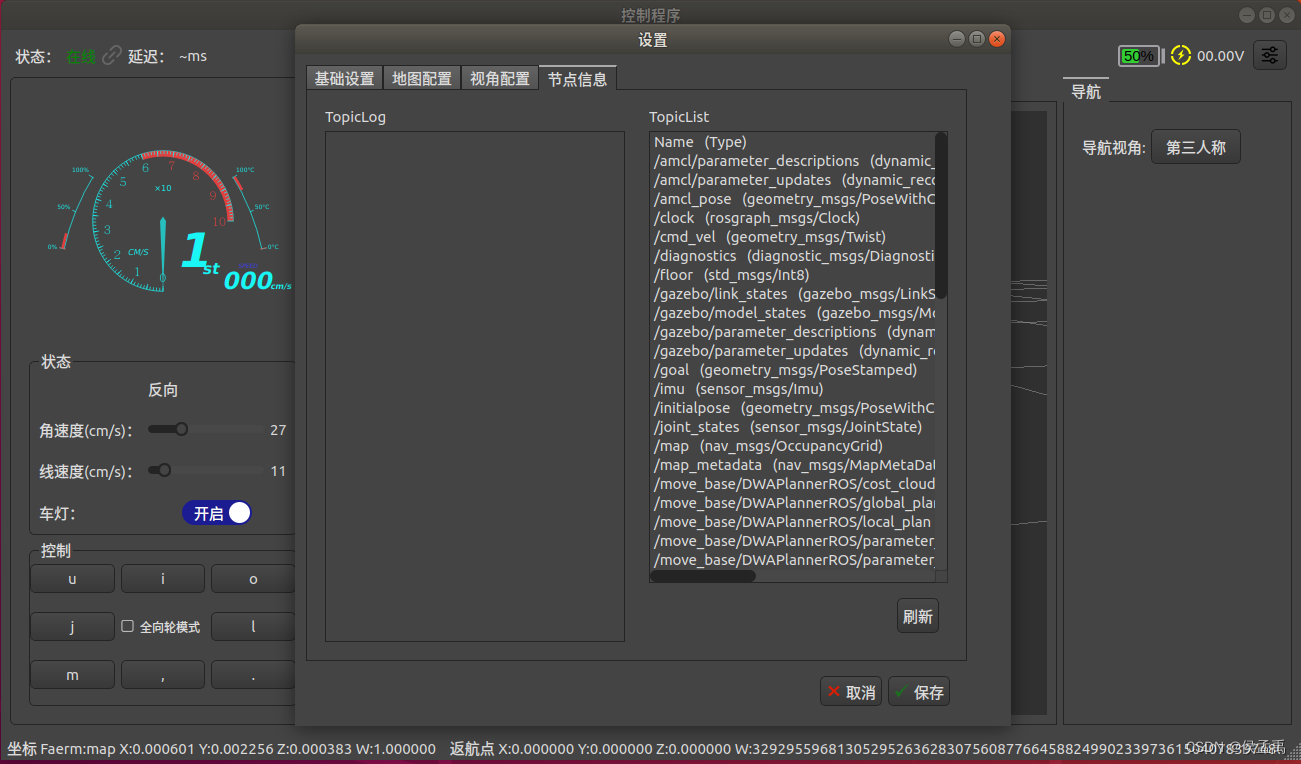
QT搭建的Ros/librviz的GUI软件
1.前言 开发初期学习了下面博主的文章,也报了他在古月局的课,相当于感谢吧。 ROS Qt5 librviz人机交互界面开发一(配置QT环境)-CSDN博客r 软件前期也是参考他的开源项目 GitHub - chengyangkj/Ros_Qt5_Gui_App …...

Docker 概述与安装
文章目录 1. Docker简介2. 传统虚拟机和容器3. Docker运行速度快的原因4. Docker软件4.1 Docker镜像4.2 Docker容器4.3 Docker仓库 5. Docker架构6. CentOS安装Docker6.1 卸载旧版本6.2 配置yum资源库6.3 安装Docker引擎6.4 启动docker引擎6.5 设置开机自启 7. 卸载Docker8. 运…...

JS作用域与作用域链
让我为大家介绍一下作用域与作用域链吧! 作用域 作用域规定了变量能够访问的“范围”,离开了这个“范围”变量便不能被访问。 作用域分为:局部作用域,全局作用域 一、局部作用域 局部作用域分为函数作用域与块作用域 1.函数作…...

elmentui 查看大图组件 点击图片关闭弹窗方法
elmentui 查看大图组件 点击图片关闭弹窗方法 html <el-imageref"Imgs":src"item.url ? item.url : ":preview-src-list"item.url ? [item.url] : []"click.stop"handlePreviewClose"class"alarm_img"/>js //图片…...
)
蓝桥杯官网练习题(最长子序列)
题目描述 我们称一个字符串S 包含字符串 T 是指 T 是 S 的一个子序列,即可以从字符串 S 中抽出若干个字符,它们按原来的顺序组合成一个新的字符串与 T 完全一样。 给定两个字符串 S 和 T,请问 T 中从第一个字符开始最长连续多少个字…...

Make sure that using this pseudorandom number generator is safe here.
问题类型:安全热点 安全问题级别:MEDIUM 一、问题代码 工具类Package: Java commons-lang3 库 RandomUtils 随机数工具类 import org.apache.commons.lang3.RandomUtils; 用法: RandomUtils.nextInt(0, 999999999) //生成 0…...

【C/C++】常见模拟题题解
题解 模拟双目运算符一元二次方程求解水仙花数统计学生成绩学生成绩管理模拟选举大小写字符转换最大公约数、最小公倍数字符串反序 模拟双目运算符 编写一个根据用户键入的两个操作数和一个双目运算符,由计算机输出结果的程序。 #include<stdio.h>int opera…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...
