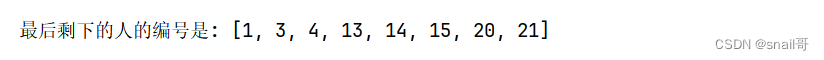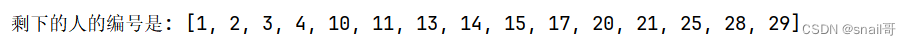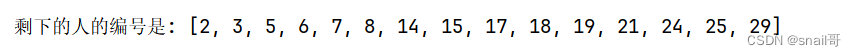每日一练:约瑟夫生者死者小游戏

1. 问题描述
约瑟夫问题(Josephus problem)是一个经典的数学和计算机科学问题,源于犹太历史学家弗拉维奥·约瑟夫斯(Flavius Josephus)的著作《犹太战记》。问题的描述如下:
在这个问题中,有n个人站成一个圈,从1到n编号。从第一个人开始,每次数m个人,数到第m个人就将其从圈中删除,然后从下一个人开始重新数,重复这个过程,直到所有人都被删除。问题是,最后剩下的那个人的编号是多少?
为了解决约瑟夫问题,可以使用递归或迭代的方法。下面是一个简单的递归解法的伪代码:
function josephus(n, m):if n == 1:return 1else:return (josephus(n - 1, m) + m - 1) % n + 1
这个递归函数的基本思想是:假设已知n-1个人的问题的解,那么在这个基础上,考虑第n个人加入的情况。在每一轮中,我们实际上将问题规模缩小为n-1个人。
注意,这里的编号是从1开始的,因为在问题的原始描述中,人的编号是从1到n的。在某些变体中,编号可能从0开始,因此在实现时需要注意这一点。
2. 解题思路
解决约瑟夫问题的一般思路是通过模拟每一轮的删除过程,不断更新当前位置,并在满足终止条件时停止模拟。下面是一种基于迭代的解题思路和设计:
解题思路:
- 初始化: 创建一个包含n个人初始编号的列表,并初始化一个变量表示当前位置。
- 循环删除过程:
- 在当前位置开始数m个人。
- 计算出要删除的人的位置。
- 从列表中删除该位置的人。
- 更新当前位置为删除位置。
- 终止条件: 当剩下的人数满足终止条件时,停止循环。
- 返回结果: 根据具体要求返回结果。在约瑟夫问题中,通常是返回最后剩下的一个人的编号或一组编号。
3. 代码实现
3.1 代码实现一
30 个人在一条船上,超载,需要 15 人下船。于是人们排成一队,排队的位置即为他们的编号。报数,从 1 开始,数到 9 的人下船。如此循环,直到船上人不能数到9人为止,问剩下的人的编号?
def josephus(n, m):# 创建一个列表,表示n个人的初始编号people = list(range(1, n + 1))# 初始化变量,表示当前位置current = 0# 循环,直到剩下8个人while len(people) > 8:# 计算下一个要删除的人的位置current = (current + m - 1) % len(people)# 删除当前位置的人del people[current]# 返回剩下的最后一个人的编号return people# 示例:有30个人,每次数9个人
result = josephus(30, 9)
print("最后剩下的人的编号是:", result)
运行效果:
3.2 代码实现二
题目修改为:
30 个人在一条船上,超载,需要 15 人下船。于是人们排成一队,排队的位置即为他们的编号。报数,从 1 开始,数到 9 的人下船。如此循环,直到船上仅剩 15 人为止,问剩下的人的编号?
def josephus(n, m, k):# 创建一个包含n个人初始编号的列表people = list(range(1, n + 1))# 初始化变量,表示当前位置current = 0# 循环,直到剩下的人数满足终止条件while len(people) > k:# 在当前位置开始数m个人,计算出要删除的人的位置current = (current + m - 1) % len(people)# 从列表中删除该位置的人del people[current]# 返回剩下的人的编号return people# 示例:有30个人,每次数9个人删除,直至剩下15个人
result = josephus(30, 9, 15)
print("剩下的人的编号是:", result)
3.3 代码实现三
题目修改为:
30 个人在一条船上,超载,需要 15 人下船。于是人们排成一队,排队的位置即为他们的编号。报数,从 5 开始,数到 9 的人下船。如此循环,直到船上仅剩 15 人为止,问剩下的人的编号?
def josephus_with_start(n, m, k, start):people = list(range(1, n + 1))current = start - 1 # 起始位置while len(people) > k:current = (current + m - 1) % len(people)del people[current]return people# 示例:有30个人,每次数9个人删除,直至剩下15个人,起始位置为5
result = josephus_with_start(30, 9, 15, 5)
print("剩下的人的编号是:", result)
3.4 代码实现四
题目修改为:
30 个人在一条船上,超载,需要 15 人下船。于是人们排成一队,排队的位置即为他们的编号。报数,从 1 开始,数到 9 的人下船,但是每隔一轮人才下船。如此循环,直到船上仅剩 15 人为止,问剩下的人的编号?
def josephus_with_custom_deletion(n, m, k, deletion_rule):people = list(range(1, n + 1))current = 0while len(people) > k:current = deletion_rule(current, m, len(people))del people[current]return people# 示例:有30个人,每次数9个人删除,直至剩下15个人,但是每隔一轮删除一个人
def custom_deletion_rule(current, m, length):return (current + m) % lengthresult = josephus_with_custom_deletion(30, 9, 15, custom_deletion_rule)
print("剩下的人的编号是:", result)
4.参考:
| https://www.runoob.com/python3/python-joseph-life-dead-game.html |

相关文章:

每日一练:约瑟夫生者死者小游戏
1. 问题描述 约瑟夫问题(Josephus problem)是一个经典的数学和计算机科学问题,源于犹太历史学家弗拉维奥约瑟夫斯(Flavius Josephus)的著作《犹太战记》。问题的描述如下: 在这个问题中,有n…...

双指针算法(题目与答案讲解)
文章目录 题目移动零复写零两数之和N数之和(>2个数) 答案讲解移动零复写零两数之和N数之和 题目 力扣 移动零 1、移动零:题目链接 复写零 2、复写零:题目链接 两数之和 3、两数之和题目链接 N数之和(>2个数) 4、N数之和(三个数、四个数) 三个数:题目链接 四个数题目链接…...
python服装电商系统vue购物商城django-pycharm毕业设计项目推荐
系统面向的使用群体为商家和消费者,商家和消费者所承担的功能各不相同,所对象的权限也各不相同。对于消费者和商家设计的功能如下: 对于消费者设计了五大功能模块: (1) 商品信息:用户可在商品…...
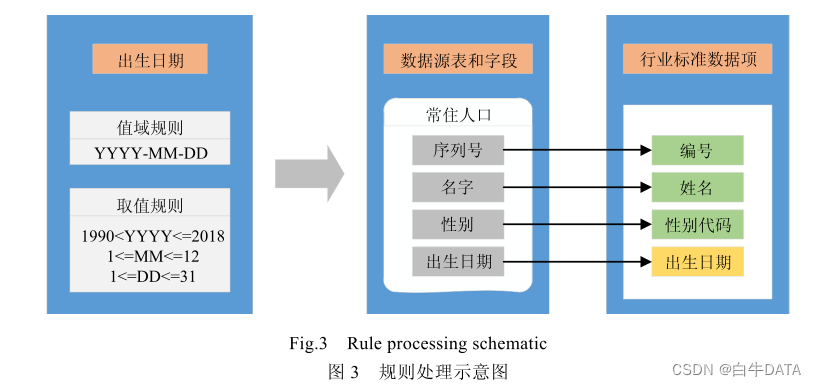
数据治理技术:研究现状与数据规范
随着信息技术的迅速发展,数据规模逐渐扩大,与此同时,劣质数据也随之而来,极大地降低了数据挖掘的质量,对信息社会造成了严重的困扰,劣质数据大量存在于很多领域和机构,国外权威机构的统计表明:美…...
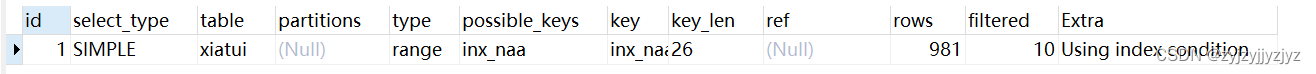
一文彻底理解索引下推
了解索引下推吗?二级索引取出的数据是依次回表还是一次回表?索引下推是为了什么发明的? 看完这个文章你将知道上面的问题。 索引下推的概念 从MySQL5.6开始引入的一个特性,索引下推通过减少回表的次数来提高数据库的查询效率; 注意&#…...
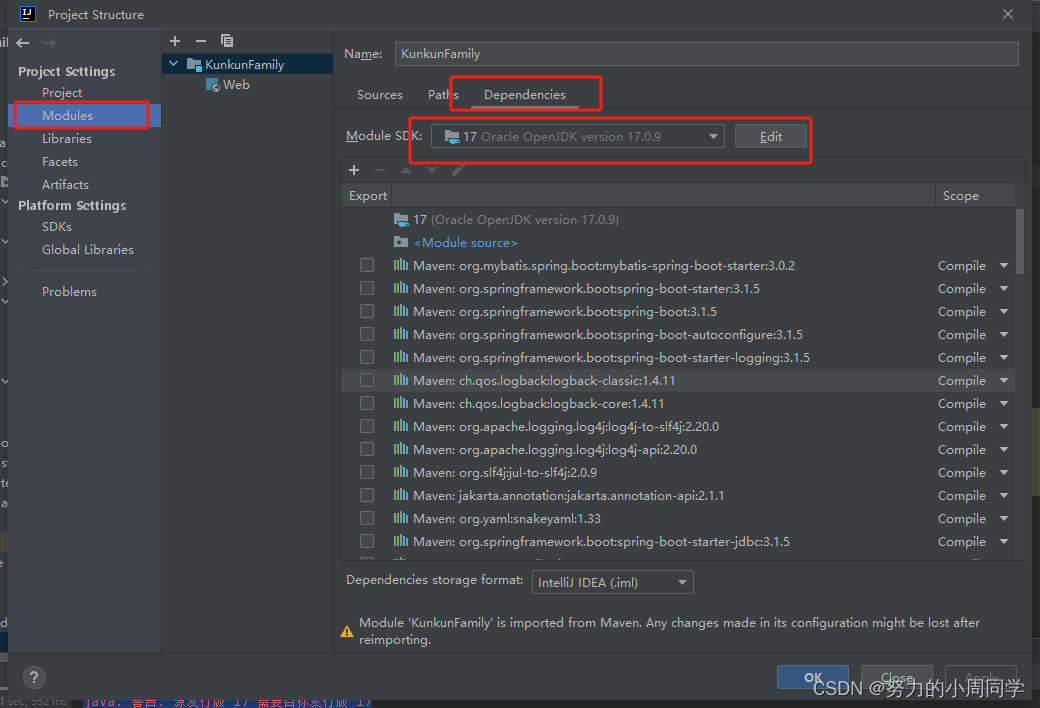
Springboot3+vue3从0到1开发实战项目(一)
一. 可以在本项目里面自由发挥拓展 二. 知识整合项目使用到的技术 后端开发 : Validation, Mybatis,Redis, Junit,SpringBoot3 ,mysql,Swagger, JDK17 ,JWT,项目部署 前端开发: Vue3,Vite&am…...

[字符串操作] 有年代的病历单
有年代的病历单 题目描述 小英是药学专业大三的学生,暑假期间获得了去医院药房实习的机会。 在药房实习期间,小英扎实的专业基础获得了医生的一致好评,得知小英在计算概论中取得过好成绩后,主任又额外交给她一项任务,…...
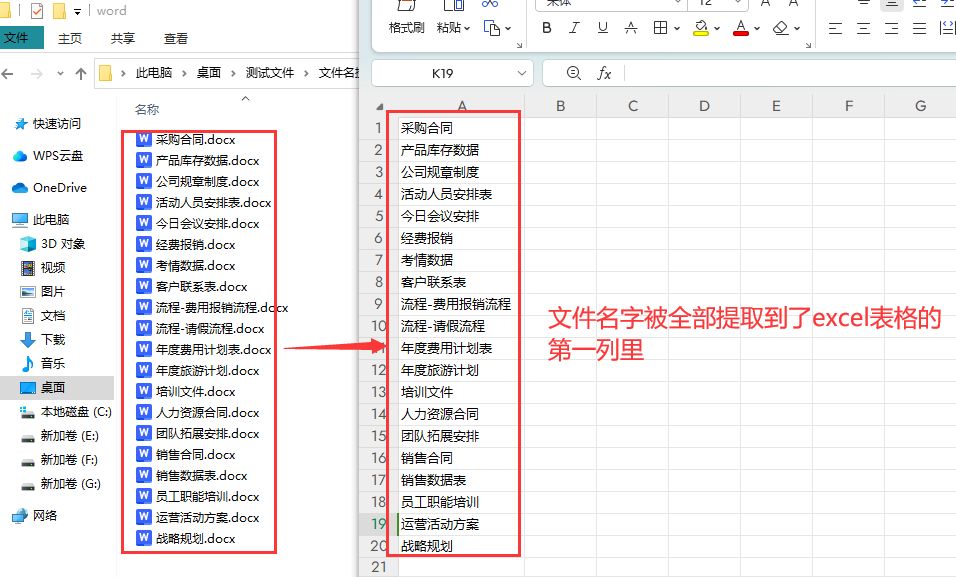
怎么批量提取文件名字到Excel中?
怎么批量提取文件名字到Excel中?Excel是由微软公司开发的一种电子表格软件,它是Microsoft Office办公套件的一部分。Excel提供了强大的数据处理和分析功能,用户可以使用Excel创建、编辑和管理电子表格,进行各种计算、数据分析、图…...
QT搭建的Ros/librviz的GUI软件
1.前言 开发初期学习了下面博主的文章,也报了他在古月局的课,相当于感谢吧。 ROS Qt5 librviz人机交互界面开发一(配置QT环境)-CSDN博客r 软件前期也是参考他的开源项目 GitHub - chengyangkj/Ros_Qt5_Gui_App …...

Docker 概述与安装
文章目录 1. Docker简介2. 传统虚拟机和容器3. Docker运行速度快的原因4. Docker软件4.1 Docker镜像4.2 Docker容器4.3 Docker仓库 5. Docker架构6. CentOS安装Docker6.1 卸载旧版本6.2 配置yum资源库6.3 安装Docker引擎6.4 启动docker引擎6.5 设置开机自启 7. 卸载Docker8. 运…...

JS作用域与作用域链
让我为大家介绍一下作用域与作用域链吧! 作用域 作用域规定了变量能够访问的“范围”,离开了这个“范围”变量便不能被访问。 作用域分为:局部作用域,全局作用域 一、局部作用域 局部作用域分为函数作用域与块作用域 1.函数作…...

elmentui 查看大图组件 点击图片关闭弹窗方法
elmentui 查看大图组件 点击图片关闭弹窗方法 html <el-imageref"Imgs":src"item.url ? item.url : ":preview-src-list"item.url ? [item.url] : []"click.stop"handlePreviewClose"class"alarm_img"/>js //图片…...
)
蓝桥杯官网练习题(最长子序列)
题目描述 我们称一个字符串S 包含字符串 T 是指 T 是 S 的一个子序列,即可以从字符串 S 中抽出若干个字符,它们按原来的顺序组合成一个新的字符串与 T 完全一样。 给定两个字符串 S 和 T,请问 T 中从第一个字符开始最长连续多少个字…...

Make sure that using this pseudorandom number generator is safe here.
问题类型:安全热点 安全问题级别:MEDIUM 一、问题代码 工具类Package: Java commons-lang3 库 RandomUtils 随机数工具类 import org.apache.commons.lang3.RandomUtils; 用法: RandomUtils.nextInt(0, 999999999) //生成 0…...

【C/C++】常见模拟题题解
题解 模拟双目运算符一元二次方程求解水仙花数统计学生成绩学生成绩管理模拟选举大小写字符转换最大公约数、最小公倍数字符串反序 模拟双目运算符 编写一个根据用户键入的两个操作数和一个双目运算符,由计算机输出结果的程序。 #include<stdio.h>int opera…...

TikTok 购物和直播的 5 个简单技巧
TikTok 的一切都很大:应用程序下载量、受众规模和病毒式营销活动。因此,该公司多方面进军社交商务也就不足为奇了。是的,这将是巨大的。自去年年底以来,TikTok Shopping 和TikTok 直播购物活动已在一些市场上线,并将于…...

神经网络中BN层简介及位置分析
1. 简介 Batch Normalization是深度学习中常用的技巧,Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift (Ioffe and Szegedy, 2015) 第一次介绍了这个方法。 这个方法的命名,明明是Standardization, 非…...

BGP基础配置
EBGP是AS之间 IBGP是AS内 R1-R2是EBGP,R4-R5是EBGP R2-R3-R4是IBGP 第一步基础配置:IP地址 [r1-GigabitEthernet0/0/0]ip ad 12.0.0.1 24 [r1-LoopBack0]ip ad 1.1.1.1 32 [r2-GigabitEthernet0/0/0]ip ad 12.0.0.2 24 [r2-LoopBack0]ip ad 2.2.2.2 32 [r2-Loop…...

【开题报告】基于深度学习的驾驶员危险行为检测系统
研究的目的、意义及国内外发展概况 研究的目的、意义:我国每年的交通事故绝对数量是一个十分巨大的数字,造成了巨大的死亡人数和经济损失。而造成交通事故的一个很重要原因就是驾驶员的各种危险驾驶操作行为。如果道路驾驶员的驾驶行为能够得到有效识别…...

Linux云服务器打包部署前端Vue项目
1. 打包 在项目包的终端使用命令打包成dist文件。 npm run build2. Linux云服务器上创建文件夹 mkdir /home/www/dist注:dist文件夹不用创建,将打包好的dist.zip放进去,然后解压就行。 3. 安装nginx yum install -y nginx4. 修改配置文件…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...