【数据结构】八大排序 (三)
目录
前言:
快速排序
快速排序非递归实现
快速排序特性总结
归并排序
归并排序的代码实现
归并排序的特性总结
计数排序
计数排序的代码实现
计数排序的特性总结
前言:
前文快速排序采用了递归实现,而递归会开辟函数栈帧,递归的深度越深,占用栈区的空间就越大,栈区的大小一般是8M,10M,当递归深度足够深时,栈区的空间就会被用完,导致栈溢出,此时需要将递归改为非递归更加稳妥,本篇继续详细解读快排的非递归实现,归并排序,计数排序;
快速排序
快速排序非递归实现
- 采用递归实现快速排序时,而递归就是不断调用单趟排序函数的功能,若不采用递归,什么可以实现不断调用单趟排序函数的功能?
- 循环;
- 循环只要满足循环条件,就会不断调用单趟排序函数的功能,但是每次递归调用时单趟排序函数的参数是变化的,而循环条件确是一成不变的,递归会在栈上建立函数栈帧,而函数栈帧里面存放下次调用该函数的参数,若采用非递归,那我们就必须把每一次循环的参数记录下来,供单趟排序使用,如何解决?
- 使用顺序栈或者链式栈记录每次函数参数,栈的实现采用动态内存开辟,存储空间是堆区开辟的空间,堆区大小可达2G;
快速排序非递归实现步骤:
- 创建一个栈,将整个序列的起始位置和结束位置入栈;
- 当栈不为空时,弹出栈顶元素,取出该区间的起始位置 left 和结束位置 right;
- 对该区间进行划分,获取划分点 keyi;
- 如果keyi左边还有元素,将左半部分的起始位置left和结束位置keyi-1入栈;
- 如果keyi右边还有元素,将右半部分的起始位置keyi+1和结束位置right入栈;
- 重复步骤2-5,直到栈为空;
- 栈的特性为后入先出,先将待排序序列的右边界 right入栈,后将待排序序列的左边界left入栈;出栈时(获取栈顶元素)就可以先取到左边界值left ,后取到右边界值right;

- 先获取栈顶元素,然后出栈,先取到0给left,后取到7给right,进行单趟排序(hoare版本)
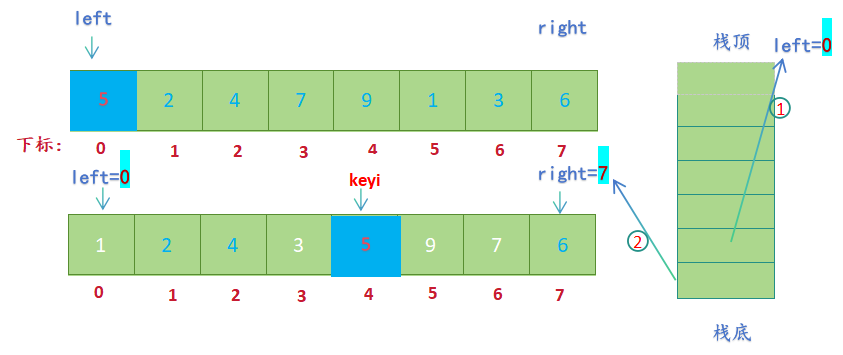
- 区间被划分为【left,keyi-1】 U keyi U 【keyi+1, right】(left=0, keyi-1=3,keyi+1=5,right=7),为了先处理划分后的左子序列,先将右子区间的边界值right keyi+1分别入栈(先入right,后入keyi+1) ,然后将左子区间的边界值keyi-1,left分别入栈(先入keyi-1, 后入left);

- 先取栈顶元素,然后出栈,先取到的元素给left ,后取到的元素给right (left=0, right=3), 进行单趟排序(hoare版本);

- keyi左边没有元素,keyi右边还有元素,将右半部分的起始位置keyi+1和结束位置right入栈(right先入栈,keyi+1后入栈)
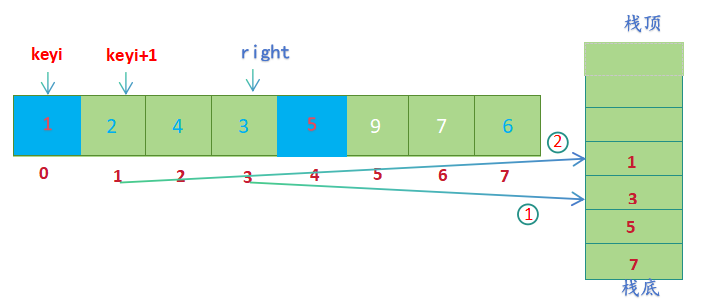
- 先取栈顶元素,然后出栈,先取到的元素给left ,后取到的元素给right (left=1, right=3), 进行单趟排序(hoare版本);

- keyi左边没有元素,keyi右边还有元素,将右半部分的起始位置keyi+1和结束位置right入栈(right先入栈,keyi+1后入栈)
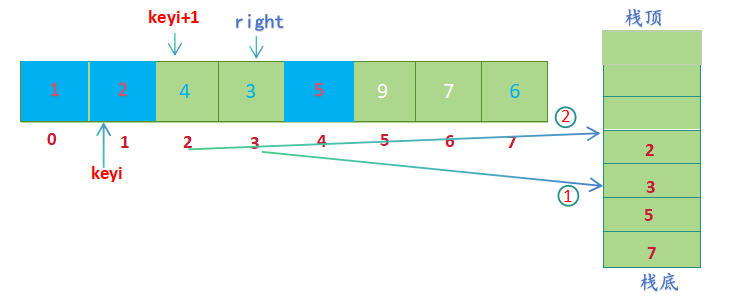

- 左子区间全部被排完,此时才可以取出5和7排右子区间,右子区间按相同流程处理即可;
顺序栈与链式栈的实现:顺序栈与链式栈_顺序栈和链栈-CSDN博客
//快排非递归实现
void QuickSortNonR(int* a, int begin, int end)
{Stack st;InitStack(&st);StackPush(&st, end);StackPush(&st, begin);while (!StackEmpty(&st)){int left = StackTop(&st);StackPop(&st);int right = StackTop(&st);StackPop(&st);int keyi = PartSort(a, left, right);//[left keyi-1] keyi [keyi+1 right]if (right > keyi + 1){StackPush(&st, right);StackPush(&st, keyi+1);}if (keyi - 1 > left){StackPush(&st, keyi - 1);StackPush(&st, left);}}DestroyStack(&st);
}快速排序特性总结
1. 时间复杂度
因为每次排序都将待排序序列分成两部分,每部分的长度大约为原序列的一半,因此需要进行logn次排序,每次排序的时间复杂度为O(n),所以快速排序的时间复杂度为O(n*logn);
2. 空间复杂度
因为每次排序需要使用递归调用,每次调用需要使用一定的栈空间,所以快速排序的空间复杂度为O(logn);
3. 算法稳定性
快速排序的算法不稳定,这是因为在排序过程中,可能会出现相同元素的相对位置发生变化的情况;当待排序序列中存在多个相同的元素时,快速排序可能会将它们分到不同的子序列中,从而导致它们的相对位置发生变化;
归并排序
归并排序的基本思想:
将待排序的序列分成若干个子序列,每个子序列都是有序的,然后再将这些有序的子序列合并成一个大的有序序列;
具体实现过程通常采用递归的方法,将序列递归地分成两半,对每一半分别进行归并排序,最后将两个有序的子序列合并成一个有序的序列;在合并的过程中,需要开辟一个数组来存储合并后的序列,然后再将临时数组中的元素拷贝回原数组中;
归并排序的基本思想可以总结为以下三个步骤:
- 分割:将待排序的序列分成若干个子序列,每个子序列都是有序的;
- 合并:将有序的子序列归并到开辟后的数组形成一个大的有序序列;
- 复制:将临时数组中的元素复制回原数组中;

归并排序的实现步骤:
- 分割:将待排序数组从中间位置分成两个子数组,直到每个子数组只有一个元素为止;
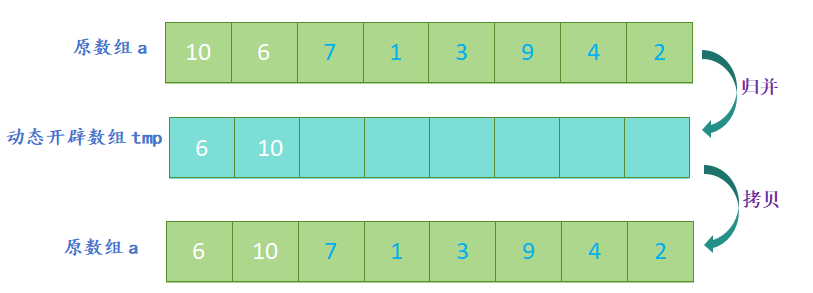
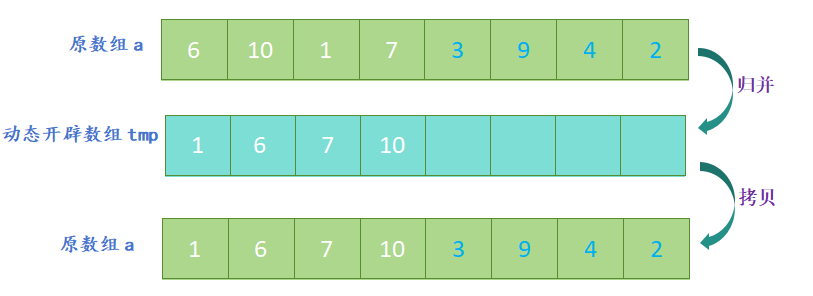
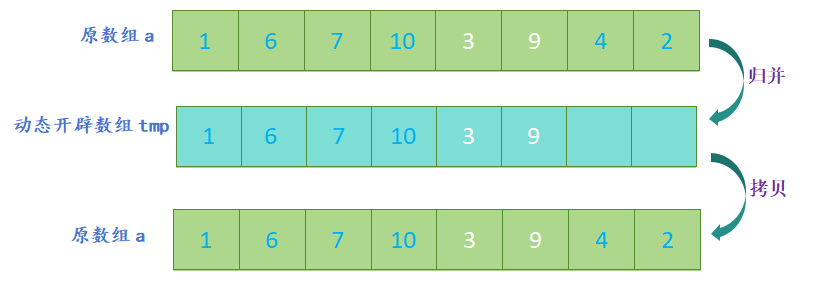
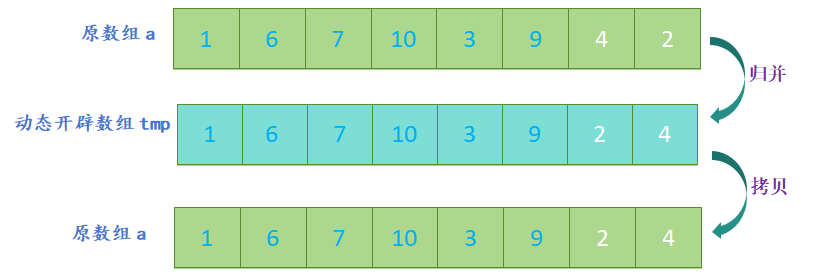
- 归并:将两个有序子数组合并成一个大的有序数组;
- 开辟一个新数组,新数组的大小与原数组大小相同,定义三个指针,分别指向两个子数组和新数组;
- 比较两个子数组的第一个元素,将较小的元素放入新数组中,并将指向该元素的指针向后移动一位;
- 重复上一步,直到其中一个子数组的元素全部放入新数组中;
- 将另一个子数组中剩余的元素依次放入新数组中;
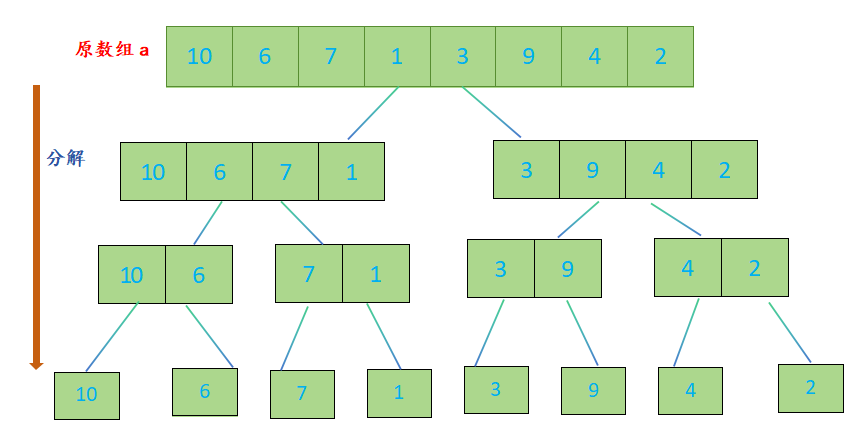

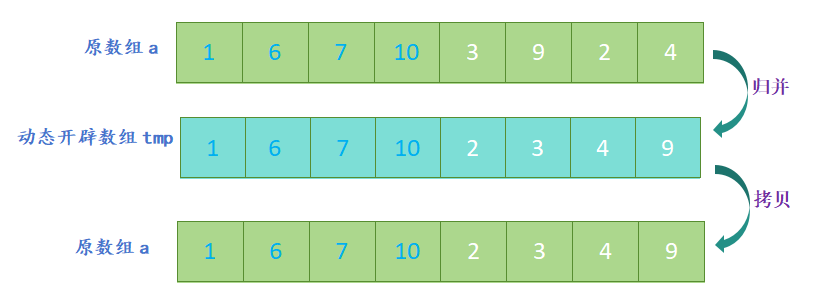
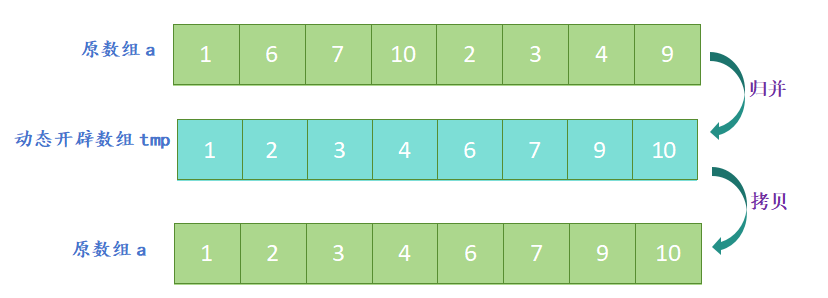
归并排序的代码实现
//归并排序(递归)
//将待排序序列不断二分,直到每个子序列只有一个元素为止,只有一个元素,序列一定有序;
//将相邻的两个子序列合并成一个有序的序列,直到所有子序列都被合并成一个完整的序列;
void SubMergeSort(int* a, int* tmp, int begin, int end)
{if (begin >= end)return;int mid = (begin + end) / 2;//划分区间为[begin,mid]U[mid+1,end]int begin1 = begin, end1 = mid;int begin2 = mid + 1, end2 = end;//递归终止的条件为区间只包含一个元素或者区间不存在;//后序遍历SubMergeSort(a, tmp, begin1, end1);SubMergeSort(a, tmp, begin2, end2);
//首先归并到tmp数组,然后拷贝到原数组;int index = begin;//tmp数组下标while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[index++] = a[begin1++];}else{tmp[index++] = a[begin2++];}}//begin1>end1与begin2>end2至少有一个发生while (begin1 <= end1){tmp[index++] = a[begin1++];}while (begin2 <= end2){tmp[index++] = a[begin2++];}//拷贝到原数组memcpy(a + begin, tmp + begin, (end - begin + 1)*sizeof(int));
}
void MergeSort(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int)*n);if (tmp == NULL){perror("malloc failed");return;}SubMergeSort(a, tmp, 0, n - 1);
}归并排序的特性总结
1. 时间复杂度
归并排序的时间复杂度可以通过递归树来分析;在递归树中,每个节点表示对一个区间进行排序的时间复杂度,而每个节点的子节点表示对该区间的两个子区间进行排序的时间复杂度,因此,递归树的深度为logn,每层的时间复杂度为O(n),因此归并排序的时间复杂度为O(nlogn);
2. 空间复杂度
归并排序的空间复杂度为O(n),因为在排序过程中需要创建一个长度为n的临时数组来存储排序结果;
3. 算法稳定性
归并排序是一种稳定的排序算法,因为在合并两个有序子序列的过程中,如果两个元素相等,那么先出现的元素会先被放入结果数组中,保证了排序的稳定性;
计数排序
计数排序的基本思想:
计数排序不是一个基于比较的排序算法,是记录数据出现次数的一种排序算法;计数排序使用一个额外的count数组,其中第i个元素是待排序数组中值等于i的元素的个数,然后根据count数组来将待排序数组中的元素排到正确的位置;

计数排序的实现步骤:
- 遍历原数组,找出原数组中的最大值max,最小值min;
- 创建count数组,数组大小为max-min+1,并将其元素初始化为0;
- 将原数组里面的值减去原数组最小值min作为count数组的下标映射下来,而count数组里面存放的值就是原数组里面值出现的次数;
- 从前向后依次填充数组,填充数组时,只需要加上这个最小值,就能还原出原来的值;
计数排序的代码实现
//计数排序
void CountSort(int* a, int n)
{//寻找最大值,最小值int min = a[0];int max = a[0];for (int i = 0; i < n; i++){if (a[i] < min)min = a[i];if (a[i]>max)max = a[i];}//确定新数组count的大小int range = max - min + 1;int* count = (int*)malloc(sizeof(int)*range);if (count == NULL){perror("malloc failed:");return;}//新数组全部初始化为0,方便计数memset(count, 0, sizeof(int)*range);//统计数据出现的次数for (int i = 0; i < n; i++){count[a[i] - min]++;}//从前向后依次填充原数组int j = 0;for (int i = 0; i < range; i++){while (count[i]--){a[j++] = i + min;}}free(count);
}计数排序的特性总结
1. 时间复杂度
计数排序的时间复杂度与待排序元素的范围相关,其时间复杂度为O(n+k),其中n为元素数量,k为元素的范围(即最大的元素与最小的元素的差加1);
2. 空间复杂度
计数排序需要额外开辟的空间大小k=max+min-1,所以空间复杂度为O(k);
3. 算法稳定性
计数排序是一个非基于比较的线性时间排序算法,是一种稳定排序;
相关文章:

【数据结构】八大排序 (三)
目录 前言: 快速排序 快速排序非递归实现 快速排序特性总结 归并排序 归并排序的代码实现 归并排序的特性总结 计数排序 计数排序的代码实现 计数排序的特性总结 前言: 前文快速排序采用了递归实现,而递归会开辟函数栈帧࿰…...
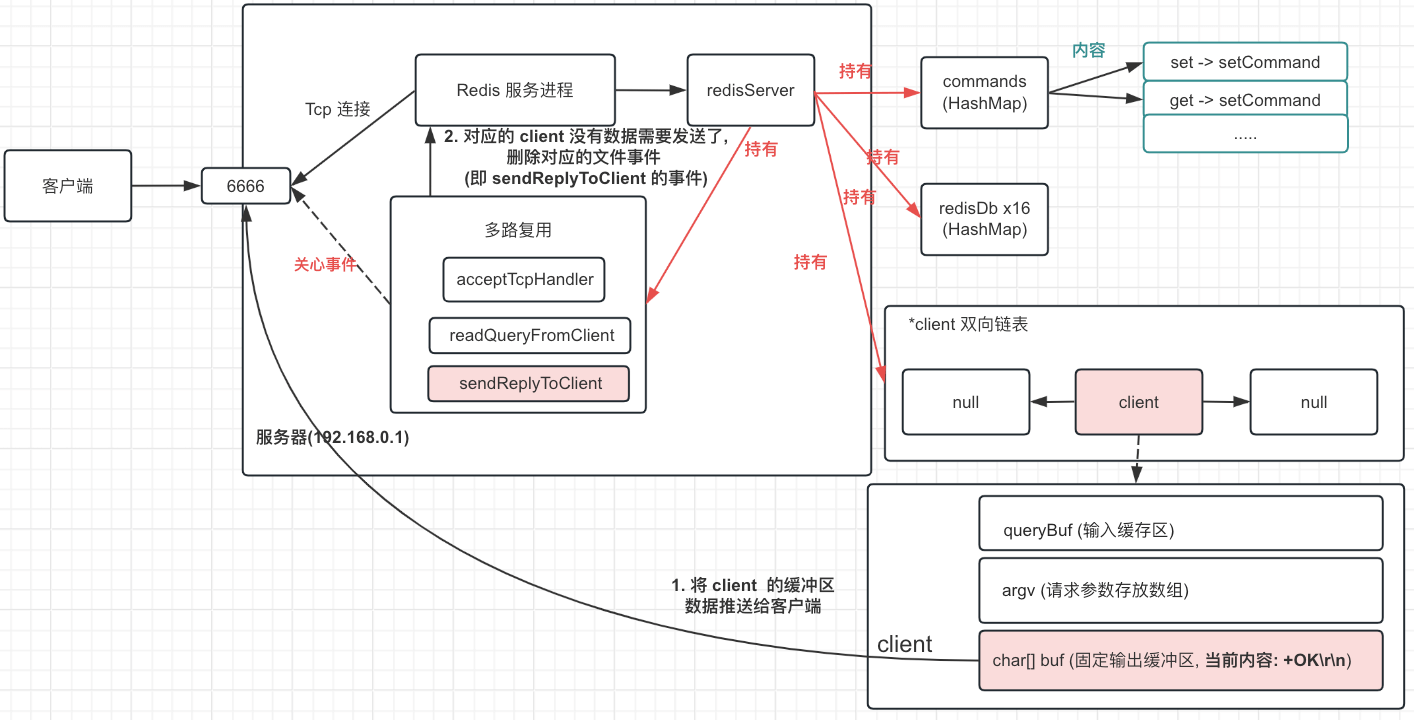
Redis 命令处理过程
我们知道 Redis 是一个基于内存的高性能键值数据库, 它支持多种数据结构, 提供了丰富的命令, 可以用来实现缓存、消息队列、分布式锁等功能。 而在享受 Redis 带来的种种好处时, 是否曾好奇过 Redis 是如何处理我们发往它的命令的呢? 本文将以伪代码的形式简单分析…...

python爬虫进阶教程之如何正确的使用cookie
文章目录 前言一、获取cookie二、程序实现三、动态获取cookie四、其他关于Python爬虫技术储备一、Python所有方向的学习路线二、Python基础学习视频三、精品Python学习书籍四、Python工具包项目源码合集①Python工具包②Python实战案例③Python小游戏源码五、面试资料六、Pytho…...

【hacker送书第4期】推荐4本Java必读书籍(各送一本)
第4期图书推荐 Java从入门到精通(第7版)内容简介参与方式 项目驱动零基础学Java内容简介参与方式 深入理解Java高并发编程内容简介参与方式 Java编程讲义内容简介参与方式 Java从入门到精通(第7版) 内容简介 《Java从入门到精通&…...

[密码学]DES
先声明两个基本概念 代换(substitution),用别的元素代替当前元素。des的s-box遵循这一设计。 abc-->def 置换(permutation),只改变元素的排列顺序。des的p-box遵循这一设计。 abc-->bac DES最核心的算法就是…...

15个超级实用的Python操作,肯定有你意想不到的!
文章目录 1)映射代理(不可变字典)2)dict 对于类和对象是不同的3) any() 和 all()4) divmod()5) 使用格式化字符串轻松检查变量6) 我们可以将浮点数转换为比率7) 用globals()和locals()显示现有的全局/本地变量8) import() 函数9) …...

GitHub上8个强烈推荐的 Python 项目
文章目录 前言1. Manim2. DeepFaceLab3. Airflow4. GPT-25. XSStrike6. 谷歌图片下载7. Gensim8. SocialMapper总结关于Python技术储备一、Python所有方向的学习路线二、Python基础学习视频三、精品Python学习书籍四、Python工具包项目源码合集①Python工具包②Python实战案例③…...

什么是依赖倒置原则
1、什么是依赖倒置原则 依赖倒置原则(Dependency Inversion Principle,DIP)是指高层模块不应该依赖于低层模块,它们都应该依赖于抽象。换句话说,具体类之间的依赖关系应该尽可能减少,而抽象类或接口之间的…...
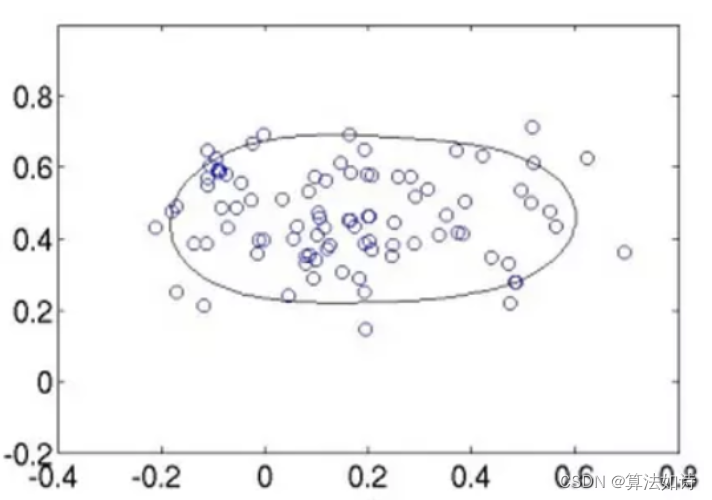
异常数据检测 | Python实现oneclassSVM模型异常数据检测
支持向量机(SVM)的异常检测 SVM通常应用于监督式学习,但OneClassSVM[8]算法可用于将异常检测这样的无监督式学习,它学习一个用于异常检测的决策函数其主要功能将新数据分类为与训练集相似的正常值或不相似的异常值。 OneClassSVM OneClassSVM的思想来源于这篇论文[9],SVM使用…...
)
using meta-SQL 使用元SQL (3)
%FirstRows Syntax %FirstRows(n) Description The %FirstRows meta-SQL variable is replaced by database-specific SQL syntax to optimize retrieval of n rows. Depending on the database, this variable optimizes: FirstRows meta-SQL变量被特定于数据库的SQL语法…...
Spinnaker 基于 docker registry 触发部署
docker registry 触发部署 Spinnaker可以通过Docker镜像的变化来触发部署,这种方法允许你在Docker镜像发生变化时自动启动新的部署流程。 示例原理如下图所示: 以下是如何在Spinnaker中实现基于Docker Registry触发部署的配置流程。最终实现的效果如下…...

2023亚马逊云科技re:Invent,在开发者板块探究如何利用技术重塑业务
美国当地时间11月27日,一年一度的亚马逊云科技re:Invent大会在美国拉斯维加斯盛大开幕。这场全球云计算领域的前沿盛会,已连续12年成为引领行业的风向标。那么本次2023亚马逊云科技re:Invent大会又有哪些可玩、可看的新项目,下面就一起来瞧一…...

JAVA 使用stream流将List中的对象某一属性创建新的List
JAVA 使用stream流将List中的对象某一属性创建新的List 1.stream流介绍 Java Stream是Java 8引入的一种新机制,它可以让我们以声明式方式操作集合数据,提供了更加简洁、优雅的集合处理方式。Stream是一个来自数据源的元素队列,并支持聚合操…...

Elasticsearch:ES|QL 函数及操作符
如果你对 ES|QL 还不是很熟悉的话,请阅读之前的文章 “Elasticsearch:ES|QL 查询语言简介”。ES|QL 提供了一整套用于处理数据的函数和运算符。 功能分为以下几类: 目录 ES|QL 聚合函数 AVG COUNT COUNT_DISTINCT 计数为近…...
SpringBoot——Swagger2 接口规范
优质博文:IT-BLOG-CN 如今,REST和微服务已经有了很大的发展势头。但是,REST规范中并没有提供一种规范来编写我们的对外REST接口API文档。每个人都在用自己的方式记录api文档,因此没有一种标准规范能够让我们很容易的理解和使用该…...
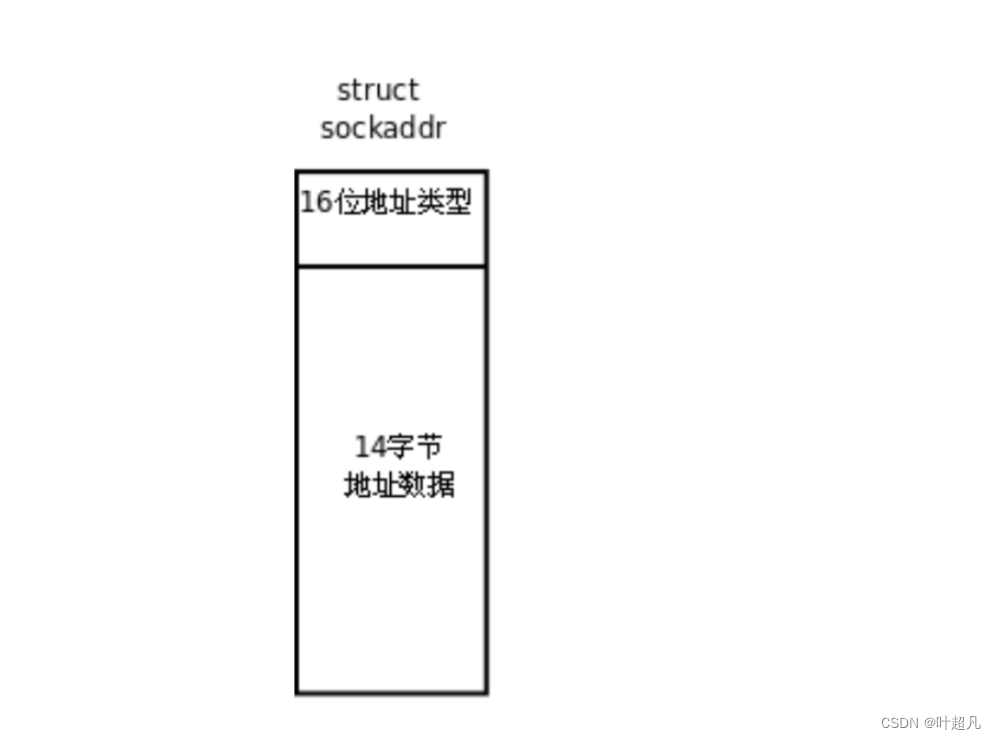
网络入门---网络编程预备知识
目录标题 ifconfigip地址和mac地址的区别端口号pid和端口号UDP和TCP的初步了解网络字节序socket套接字 ifconfig 通过指令ifconfig便可以查看到两个网络接口: 我们当前使用的是一个linux服务器并是一个终端设备,所以他只需要一个接口用来入网即可&…...

记录一次YAMLException异常
记录一次YAMLException异常 ✅作者简介:大家好,我是Leo,热爱Java后端开发者,一个想要与大家共同进步的男人😉😉 🍎个人主页:Leo的博客 💞当前专栏: 报错以及B…...

calendar --- 日历相关函数
calendar --- 日历相关函数 源代码: Lib/calendar.py 这个模块让你可以输出像 Unix cal 那样的日历,它还提供了其它与日历相关的实用函数。 默认情况下,这些日历把星期一作为一周的第一天,星期天作为一周的最后一天(这…...

中国信息通信研究院产业与规划研究所校招一面、二面内容
本文介绍2024届秋招中,中国信息通信研究院的数字孪生智慧城市研究员岗位一面、二面的面试基本情况、提问问题等。 10月投递了中国信息通信研究院的数字孪生智慧城市研究员岗位,所在部门为数字孪生与城市数字化研究部。目前完成了一面与二面,在…...

一些数据库学习的小结
一些数据库学习的小结: SQL: 遵循ACID原则。支持Transaction。适合在线交易处理(OLTP),不适合在线分析处理(OLAP)。例子有 MySQL 读写效率 单机约1KQPS POSTGRESQL NoSQL: 遵循BASE原则。不支持Transaction。例子有 DynamoDB - Amazon Key-Value BigTa…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...
