当前位置： 首页 > news >正文

视觉SLAM十四讲 ch3 (三维空间刚体运动)笔记

news 2025/7/1 22:30:32

本讲目标

●理解三维空间的刚体运动描述方式:旋转矩阵、变换矩阵、四元数和欧拉角。
●学握Eigen库的矩阵、几何模块使用方法。

旋转矩阵、变换矩阵

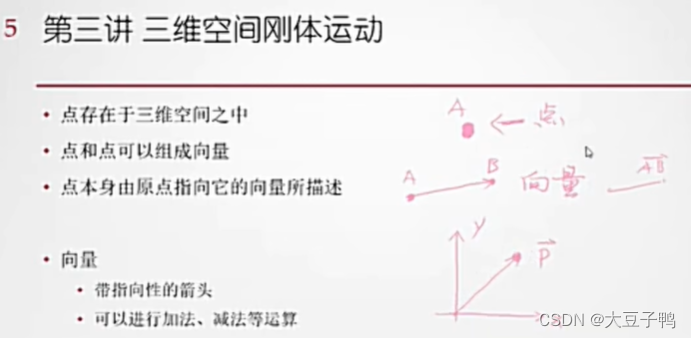
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

向量外积

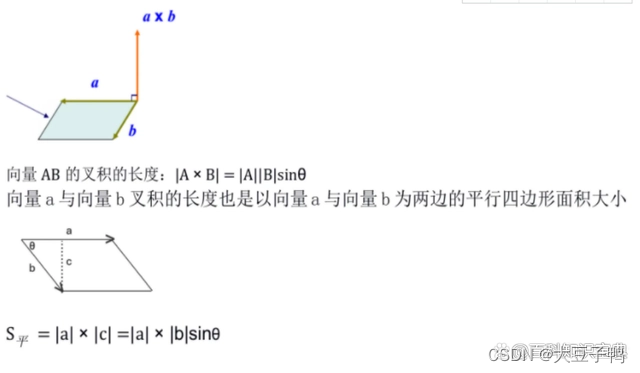
向量外积（又称叉积或向量积）是一种重要的向量运算，它表示两个向量所形成的平行四边形的面积。在几何学中，向量外积的大小是表示两个向量所形成的平行四边形的面积。

a x b 几何意义：a转到b右手坐标系的方向
a x b 大小：就是两个向量所围成的平行四边形的面积。

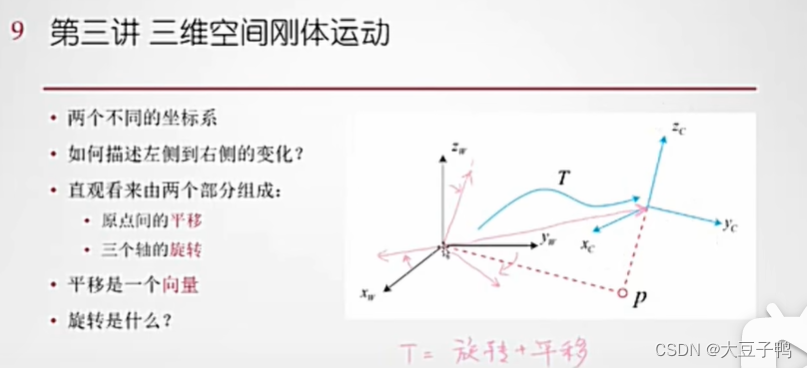
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
xw世界坐标，xc表示camera相机坐标
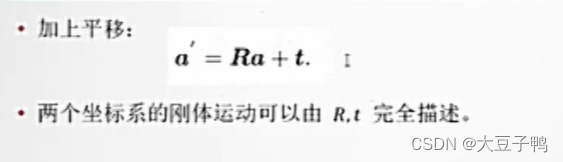
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
好处：将旋转和平移的动作放在一个矩阵中，这样每次变换就可以先进行旋转和平移动作的全部叠加，变换矩阵。

在这里插入图片描述
TWR 表示机器人坐标在世界坐标下的位姿,TRW表示世界坐标在机器人坐标下的位姿。

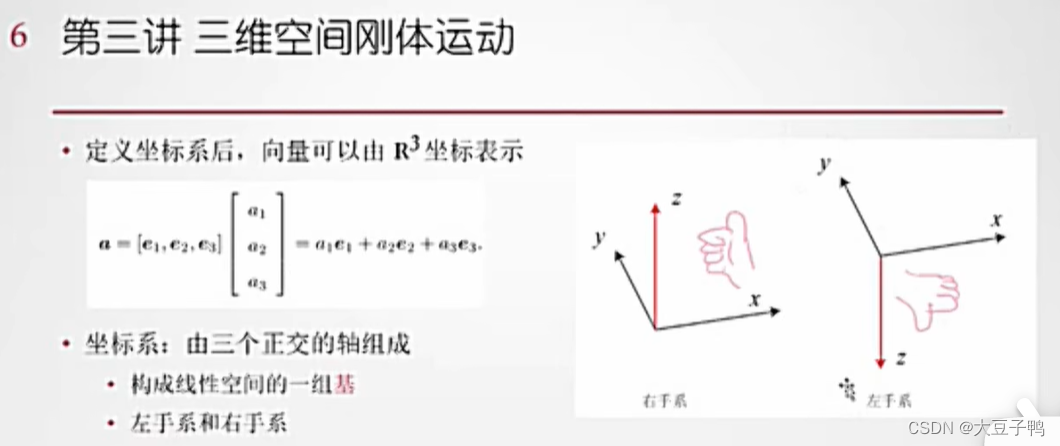
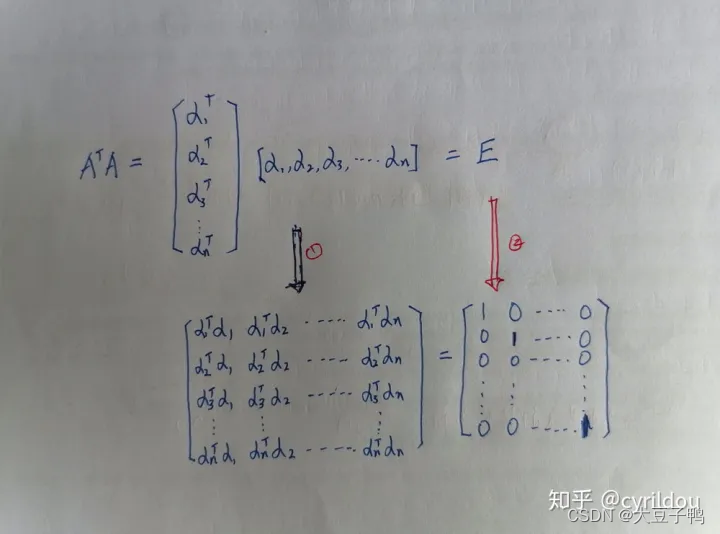
正交矩阵

正交矩阵是指其转置等于逆的矩阵，性质是逆也是正交阵、积也是正交阵。
在这里插入图片描述
正交：可以简单理解成就是垂直.

我们假设A是一个列向量矩阵，标识为 A=[ α1,α2,α3·····αn] ，那么按照定义就是：
在这里插入图片描述

旋转向量和欧拉角

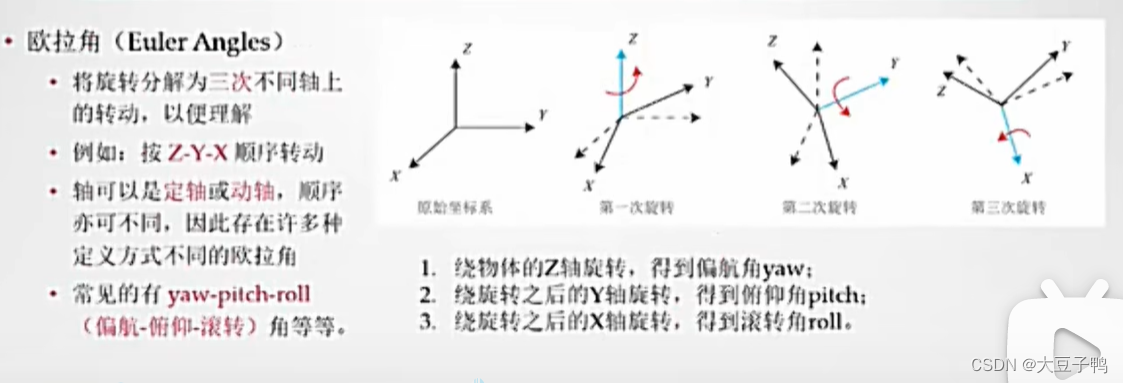
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

欧拉角：在三维空间中通过指定与三个旋转轴相关联的三个角度来最小参数化表示任意方向。
一共有3种欧拉角：俯仰角(Pitch)、偏航角(Yaw)和滚转角(Roll)

根据不同的旋转顺序，可以得到很多种欧拉角。

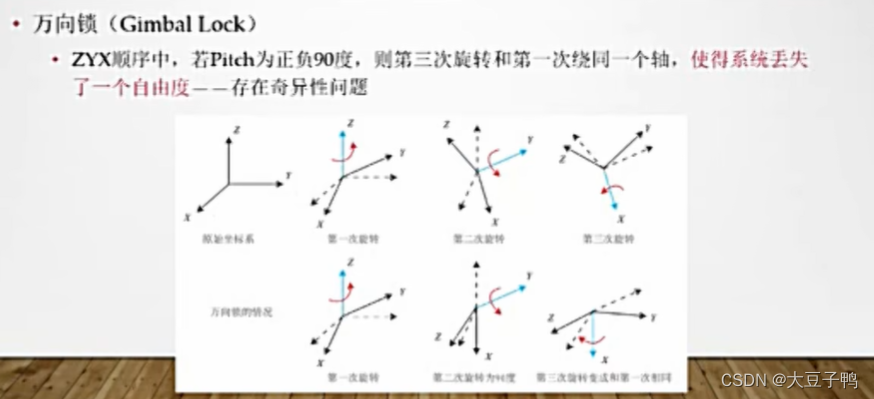
万向锁

在这里插入图片描述
在这里插入图片描述

四元数

在这里插入图片描述
在这里插入图片描述
四元数可以看成扩展的复数，有固定的运算。
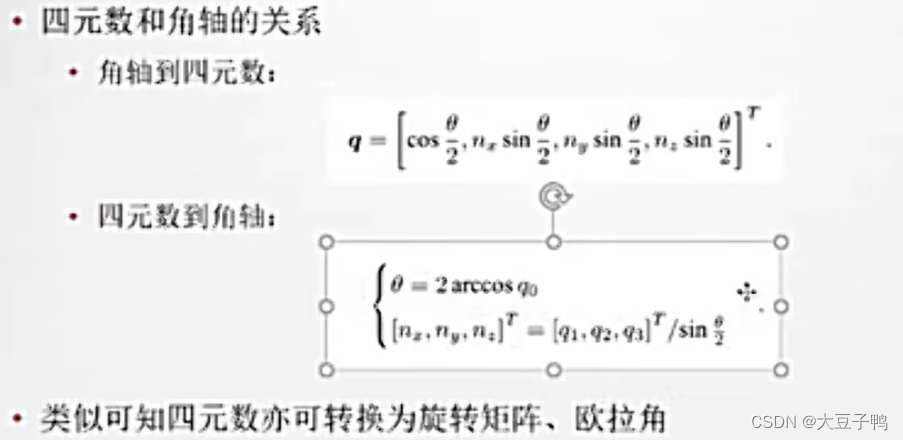
在这里插入图片描述
在这里插入图片描述
任意一个旋转都可以那一个四元数表示出来，不像欧拉角会受到限制。

参考链接：

向量外积的几何意义是什么
正交矩阵定义和性质
正交矩阵

相关文章：

视觉SLAM十四讲 ch3 (三维空间刚体运动)笔记

本讲目标 ●理解三维空间的刚体运动描述方式:旋转矩阵、变换矩阵、四元数和欧拉角。 ●学握Eigen库的矩阵、几何模块使用方法。 旋转矩阵、变换矩阵 向量外积 向量外积（又称叉积或向量积）是一种重要的向量运算，它表示两个向量所形成的平行…...

编程日记 2023/3/1 22:55:42

问题解决：java.net.SocketTimeoutException: Read timed out

简单了解Sockets Sockets：两个计算机应用程序之间逻辑链接的一个端点，是应用程序用来通过网络发送和接收数据的逻辑接口 是IP地址和端口号的组合每个Socket都被分配了一个用于标识服务的特定端口号基于连接的服务使用基于tcp的流Sockets Java为客户端…...

编程日记 2023/3/1 22:54:38

前端代码优化方法

1.封装的css样式，增加样式复用性。如果页面加载10个css文件,每个文件1k，那么也要比只加载一个100k的css文件慢 2.减少css嵌套，最好不要嵌套三层以上 3.不要在ID选择器前面进行嵌套，ID本来就是唯一的而且权限值大，嵌套完…...

编程日记 2023/3/1 22:53:31

【批处理脚本】-1.16-文件内字符串查找增强命令findstr

"><--点击返回「批处理BAT从入门到精通」总目录--> 共9页精讲（列举了所有findstr的用法，图文并茂，通俗易懂） 在从事“嵌入式软件开发”和“Autosar工具开发软件”过程中，经常会在其集成开发环境IDE（CodeWarrior，S32K DS，Davinci，EB Tresos，ETAS…）中…...

编程日记 2023/3/1 22:52:26

三天吃透Redis面试八股文

本文已经收录到Github仓库&#xff0c;该仓库包含计算机基础、Java基础、多线程、JVM、数据库、Redis、Spring、Mybatis、SpringMVC、SpringBoot、分布式、微服务、设计模式、架构、校招社招分享等核心知识点&#xff0c;欢迎star~ Github地址&#xff1a;https://github.com/…...

编程日记 2023/3/1 22:51:20

数据湖架构Hudi（三）Hudi核心概念

三、Apache Hudi核心概念 3.1 基本概念 Hudi 提供了Hudi 表的概念&#xff0c; 这些表支持CRUD操作&#xff0c; 可以利用现有的大数据集群比如HDFS做数据文件存储&#xff0c; 然后使用SparkSQL或Hive等分析引擎进行数据分析查询。 Hudi表的三个主要组件&#xff1a; 有序的…...

编程日记 2023/3/1 22:50:16

在数字优先的世界中打击知识产权盗窃

在当今数据驱动的世界中&#xff0c;全球许多组织所面临的期望和需求正在达到前所未有的水平。 为了迎接挑战&#xff0c;数据驱动的方法是必要的&#xff0c;需要有效的数字化转型来提高运营效率、简化流程并从遗留技术中获得更多收益。 但是&#xff0c;虽然数字优先方法可…...

编程日记 2023/3/1 22:49:09

机器学习算法原理——逻辑斯谛回归

文章目录逻辑斯谛回归二项逻辑斯谛回归模型极大似然估计多项逻辑斯谛回归模型总结归纳逻辑斯谛回归 写在前面&#xff1a;逻辑斯谛回归最初是数学家 Verhulst 用来研究人口增长是所发现的&#xff0c;是一个非常有趣的发现过程&#xff0c; b 站有更详细的背景及过程推导&…...

编程日记 2023/3/1 22:48:01

【华为OD机试 】最优资源分配/芯片资源占用（C++ Java JavaScript Python）

文章目录 题目描述输入描述输出描述备注用例题目解析C++JavaScriptJavaPython题目描述 某块业务芯片最小容量单位为1.25G，总容量为M*1.25G，对该芯片资源编号为1，2，…，M。该芯片支持3种不同的配置，分别为A、B、C。 配置A：占用容量为 1.25 * 1 = 1.25G配置B：占用容量为 …...

编程日记 2023/3/1 22:46:57

600 条最强 Linux 命令总结

1、基本命令 uname -m 显示机器的处理器架构 uname -r 显示正在使用的内核版本 dmidecode -q 显示硬件系统部件 &#xff08;SMBIOS / DMI&#xff09; hdparm -i /dev/hda 罗列一个磁盘的架构特性 hdparm -tT /dev/sda 在磁盘上执行测试性读取操作系统信息 arch 显示机器…...

编程日记 2023/3/1 22:45:52

python自学之《21天学通Python》(15)——第18章 数据结构基础

数据结构是用来描述一种或多种数据元素之间的特定关系&#xff0c;算法是程序设计中对数据操作的描述&#xff0c;数据结构和算法组成了程序。对于简单的任务&#xff0c;只要使用编程语言提供的基本数据类型就足够了。而对于较复杂的任务&#xff0c;就需要使用比基本的数据类…...

编程日记 2023/3/1 22:44:47

从功能到自动化，熬夜3天整理出这一份2000字学习指南~

学习自动化这个想法&#xff0c;其实自己在心里已经琢磨了很久&#xff0c;就是一直没付诸实践&#xff0c;觉得现在手工测试已经能满足当前的工作需要&#xff0c;不想浪费时间去学习新的东西&#xff0c;有点时间还不如刷刷视频、看看小说等。 第一次有学习Selenium的冲动是…...

编程日记 2023/3/1 22:43:42

客户端攻击（溯源攻击，获取客户端信息）

目录 背景 为什么 示例 探索HTML应用程序 HTA攻击行为（Powershell代码） 背景 如果创建的文件扩展名为.hta而不是.html，Internet Explorer将自动将其解释为html应用程序，并提供使...

编程日记 2023/3/1 22:42:37

visual studio 2022 社区版 c# 环境搭建及安装使用【图文解析-小白版】

visual studio 2022 社区版 c# 环境搭建及安装使用【图文解析-小白版】visual studio 安装 C# 环境安装流程创建c#窗体应用程序visual studio 安装 C# 环境 首先&#xff0c;进入其官网下载对应的visual studio社区版本&#xff0c;官网链接: https://visualstudio.microsoft…...

编程日记 2023/3/1 22:41:33

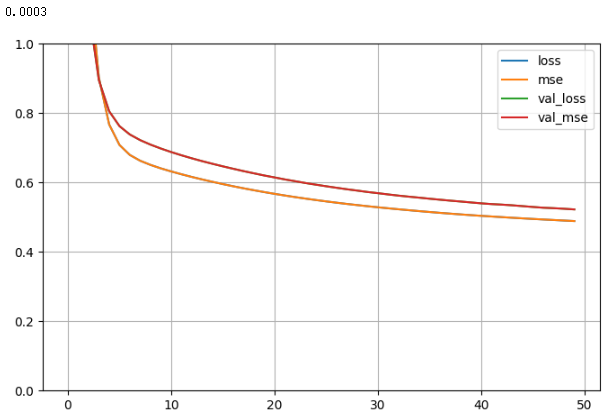
21- 神经网络模型_超参数搜索 (TensorFlow系列) (深度学习)

知识要点 fetch_california_housing&#xff1a;加利福尼亚的房价数据&#xff0c;总计20640个样本&#xff0c;每个样本8个属性表示&#xff0c;以及房价作为target 超参数搜索的方式: 网格搜索, 随机搜索, 遗传算法搜索, 启发式搜索 超参数训练后用&#xff1a; gv.estimat…...

编程日记 2023/3/1 22:40:27

《NFL橄榄球》：芝加哥熊·橄榄1号位

芝加哥熊&#xff08;英语&#xff1a;Chicago Bears&#xff09;是一支职业美式橄榄球球队。位于伊利诺伊州的芝加哥。现时为全国橄榄球联盟的国家联盟北区的球队。他们曾经赢出九次美式橄榄球比赛的冠军&#xff0c;分别为八次旧制全国橄榄球联盟和一次超级碗冠军&#xff08…...

编程日记 2023/3/1 22:39:23

【ES】Elasticsearch核心基础概念：文档与索引

es的核心概念主要是&#xff1a;index(索引)、Document(文档)、Clusters(集群)、Node(节点)与实例&#xff0c;下面我们先来了解一下Document与Index。 RESTful APIs 在讲解Document与Index概念之前&#xff0c;我们先来了解一下RESTful APIs&#xff0c;因为下面讲解Documen…...

编程日记 2023/3/1 22:38:19

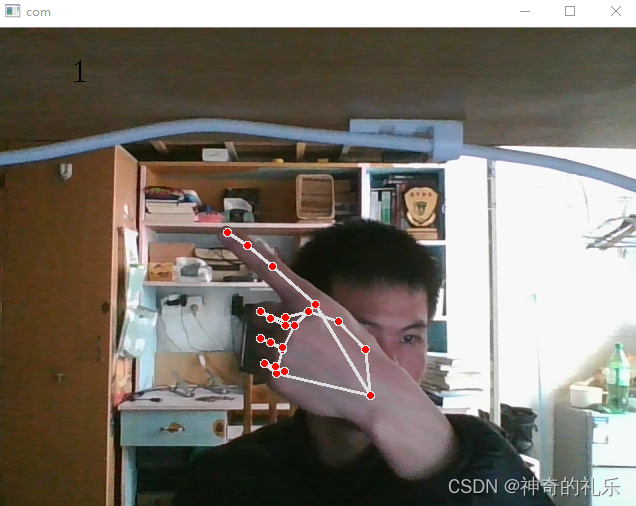
实时手势识别(C++与python都可实现)

一、前提配置&#xff1a; Windows&#xff0c;visual studio 2019&#xff0c;opencv&#xff0c;python10&#xff0c;opencv-python&#xff0c;numpy&#xff0c;tensorflow&#xff0c;mediapipe&#xff0c;math 1.安装python环境 这里我个人使用的安装python10&#…...

编程日记 2023/3/1 22:37:13

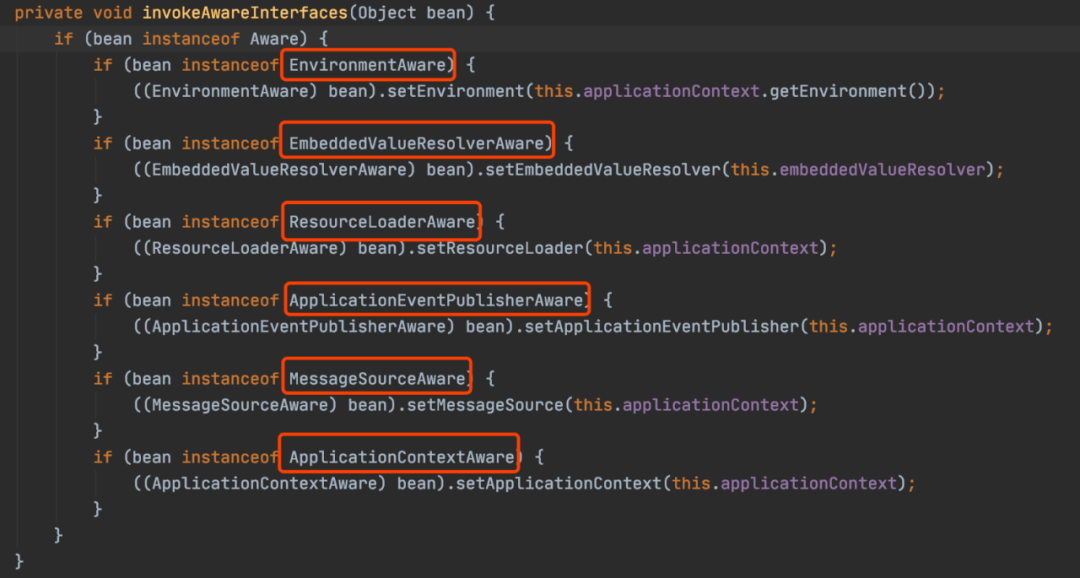
15个Spring扩展点，一般人知道的不超过5个！

Spring的核心思想就是容器&#xff0c;当容器refresh的时候&#xff0c;外部看上去风平浪静&#xff0c;其实内部则是一片惊涛骇浪&#xff0c;汪洋一片。Spring Boot更是封装了Spring&#xff0c;遵循约定大于配置&#xff0c;加上自动装配的机制。很多时候我们只要引用了一个…...

编程日记 2023/3/1 22:36:08

Elasticsearch：以 “Painless” 方式保护你的映射

Elasticsearch 是一个很棒的工具&#xff0c;可以从各种来源收集日志和指标。 它为我们提供了许多默认处理&#xff0c;以便提供最佳用户体验。 但是&#xff0c;在某些情况下&#xff0c;默认处理可能不是最佳的&#xff08;尤其是在生产环境中&#xff09;&#xff1b; 因此&…...

编程日记 2023/3/1 22:35:04

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)

题目&#xff1a;3442. 奇偶频次间的最大差值 I 思路 &#xff1a;哈希&#xff0c;时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况&#xff0c;哈希表这里用数组即可实现。 C版本&#xff1a; class Solution { public:int maxDifference(string s) {int a[26]…...

编程新知 2025/6/29 13:24:25

【网络安全产品大调研系列】2. 体验漏洞扫描

前言 2023 年漏洞扫描服务市场规模预计为 3.06&#xff08;十亿美元&#xff09;。漏洞扫描服务市场行业预计将从 2024 年的 3.48&#xff08;十亿美元&#xff09;增长到 2032 年的 9.54&#xff08;十亿美元&#xff09;。预测期内漏洞扫描服务市场 CAGR&#xff08;增长率&…...

编程新知 2025/6/29 11:54:08

DAY 47

三、通道注意力 3.1 通道注意力的定义 # 新增&#xff1a;通道注意力模块&#xff08;SE模块&#xff09; class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

编程新知 2025/6/29 11:34:05

五年级数学知识边界总结思考-下册

目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解&#xff1a;由来、作用与意义**一、知识点核心内容****二、知识点的由来&#xff1a;从生活实践到数学抽象****三、知识的作用&#xff1a;解决实际问题的工具****四、学习的意义&#xff1a;培养核心素养…...

编程新知 2025/6/20 13:47:44

计算机基础知识解析：从应用到架构的全面拆解

目录 前言 1、 计算机的应用领域&#xff1a;无处不在的数字助手 2、 计算机的进化史&#xff1a;从算盘到量子计算 3、计算机的分类&#xff1a;不止 “台式机和笔记本” 4、计算机的组件&#xff1a;硬件与软件的协同 4.1 硬件&#xff1a;五大核心部件 4.2 软件&#…...

编程新知 2025/6/26 11:22:13

怎么让Comfyui导出的图像不包含工作流信息，

为了数据安全&#xff0c;让Comfyui导出的图像不包含工作流信息&#xff0c;导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo&#xff08;推荐&#xff09;​​ 在 save_images 方法中&#xff0c;​​删除或注释掉所有与 metadata …...

编程新知 2025/6/21 15:45:49

「Java基本语法」变量的使用

变量定义 变量是程序中存储数据的容器&#xff0c;用于保存可变的数据值。在Java中&#xff0c;变量必须先声明后使用&#xff0c;声明时需指定变量的数据类型和变量名。 语法 数据类型 变量名 [ 初始值]; 示例&#xff1a;声明与初始化 public class VariableDemo {publi…...

编程新知 2025/6/25 1:01:32

在MobaXterm 打开图形工具firefox

目录 1.安装 X 服务器软件 2.服务器端配置 3.客户端配置 4.安装并打开 Firefox 1.安装 X 服务器软件 Centos系统 # CentOS/RHEL 7 及之前&#xff08;YUM&#xff09; sudo yum install xorg-x11-server-Xorg xorg-x11-xinit xorg-x11-utils mesa-libEGL mesa-libGL mesa-…...

编程新知 2025/6/23 3:43:28

如何在Spring Boot中使用注解动态切换实现

还在用冗长的if-else或switch语句管理多个服务实现？ 相信不少Spring Boot开发者都遇到过这样的场景：需要根据不同条件动态选择不同的服务实现。 如果告诉你可以完全摆脱条件判断，让Spring自动选择合适的实现——只需要一个注解，你是否感兴趣？ 本文将详细介绍这种优雅的…...

编程新知 2025/6/20 11:05:55

小白的进阶之路系列之十四----人工智能从初步到精通pytorch综合运用的讲解第七部分

通过示例学习PyTorch 本教程通过独立的示例介绍PyTorch的基本概念。 PyTorch的核心提供了两个主要特性： 一个n维张量，类似于numpy，但可以在gpu上运行 用于构建和训练神经网络的自动微分 我们将使用一个三阶多项式来拟合问题 y = s i n ( x ) y=sin(x) y=sin(x)，作为我们的…...

编程新知 2025/6/17 14:59:20