acwing算法基础之数学知识--求组合数进阶版
目录
- 1 基础知识
- 2 模板
- 3 工程化
1 基础知识
请明确如下关于取余的基本定理:
- 数a和数b的乘积模上p,等于数a模上p和数b模上p的乘积。即,
( a ⋅ b ) m o d p = ( a m o d p ) ⋅ ( b m o d p ) (a \cdot b ) \ mod \ p = (a \ mod \ p) \cdot (b \ mod \ p) (a⋅b) mod p=(a mod p)⋅(b mod p) - 数a除以数b的结果模上p,并不等于数a模上p除以数b模上p。即,
( a / b ) m o d p ≠ ( a m o d p ) / ( b m o d p ) (a/b)\ mod \ p \neq (a \ mod \ p) / (b \ mod \ p) (a/b) mod p=(a mod p)/(b mod p)
(一)
题目要求:求组合数模上p的结果,即
C n k m o d p = ? C_n^k \ mod\ p =? Cnk mod p=?
其中 p = 1 e 9 + 7 p=1e9+7 p=1e9+7,是一个质数。
重新考虑组合数 C n k C_n^k Cnk的计算公式,
C n k m o d p = n ! k ! ⋅ ( n − k ) ! m o d p C_n^k \ mod \ p=\frac{n!}{k!\cdot (n-k)!} \ mod \ p Cnk mod p=k!⋅(n−k)!n! mod p
记数 k ! k! k!模p的乘法逆元为x,数 ( n − k ) ! (n-k)! (n−k)!模p的乘法逆元为y,则上式可写成,
n ! k ! ⋅ ( n − k ) ! m o d p = n ! ⋅ x ⋅ y m o d p = ( n ! m o d p ) ⋅ ( x m o d p ) ⋅ ( y m o d p ) \frac{n!}{k!\cdot (n-k)!} \ mod \ p=n! \cdot x\cdot y \ mod \ p=(n! \ mod \ p)\cdot (x \ mod \ p) \cdot (y \ mod \ p) k!⋅(n−k)!n! mod p=n!⋅x⋅y mod p=(n! mod p)⋅(x mod p)⋅(y mod p)
那么,考虑数 k ! k! k!模p的乘法逆元x,由于p是质数,故x可由下式计算,
x m o d p = ( k ! ) p − 2 m o d p x \ mod\ p = (k!)^{p-2} \ mod \ p x mod p=(k!)p−2 mod p
观察可以推导出其递推公式,
( k ! ) p − 2 m o d p = ( ( k − 1 ) ! ) p − 2 ⋅ k p − 2 m o d p (k!)^{p-2} \ mod \ p = ((k-1)!)^{p-2}\cdot k^{p-2} \ mod \ p (k!)p−2 mod p=((k−1)!)p−2⋅kp−2 mod p
而对于 k p − 2 m o d p k^{p-2}\ mod \ p kp−2 mod p,可以快速幂在 O ( l o g N ) O(logN) O(logN)时间复杂度下求解。
故综合上述,可以预处理出阶乘和阶乘的逆元,那么答案可以表示如下,
f a c t [ n ] ⋅ i n f a c t [ k ] ⋅ i n f a c t [ n − k ] m o d p fact[n] \cdot infact[k] \cdot infact[n-k] \ mod \ p fact[n]⋅infact[k]⋅infact[n−k] mod p
将上述过程,用代码表述如下,
const int N = 1e5 + 10, mod = 1e9 + 7;
int fact[N], infact[N];int qmi(int a, int k, int p) {long long res = 1;while (k) {if (k & 1) {res = res * a % p;} k >>= 1;a = (long long)a * a % p;}return res;
}void init() {fact[0] = infact[0] = 1;for (int i = 1; i < N; ++i) {fact[i] = (long long)fact[i-1] * i % mod;infact[i] = (long long)infact[i-1] * qmi(i, mod - 2, mod) % mod;}return;
}
(二)
题目要求:
C n k m o d p = ? C_n^{k} \ mod \ p = ? Cnk mod p=?
其中 n n n和 k k k的数据范围在 1 0 18 10^{18} 1018之内,而 p p p是质数,且它的范围在 1 0 6 10^6 106以内。
对于上述特别大的组合数求解,一般引入Lucas定理。
Lucas定理:当模数p是质数时,有以下等式成立,
C n k m o d p = C n m o d p k m o d p ⋅ C n / p k / p m o d p C_n^k \ mod \ p =C_{n \ mod \ p} ^ {k \ mod \ p } \cdot C_{n/p}^{k/p} \ mod \ p Cnk mod p=Cn mod pk mod p⋅Cn/pk/p mod p
其中 k m o d p k\ mod\ p k mod p和 n m o d p n\ mod\ p n mod p是 p p p以内的数,可直接计算组合数 C n m o d p k m o d p C_{n\ mod\ p}^{k \ mod \ p} Cn mod pk mod p;而对于 C n / p k / p C_{n/p}^{k/p} Cn/pk/p,则递归使用Lucas定理计算。
故,代码如下所示,
int qmi(int a, int k, int p) {long long res = 1;while (k) {if (k & 1) res = res * a % p;k >>= 1;a = (long long)a * a % p;}return res;
}int C(int a, int b, int p) {if (b > a) return 0; //无效值,返回0long long res = 1;for (int i = 1, j = a; i <= b; ++i, --j) {res = res * j % p;res = res * qmi(i, p - 2, p) % p;}return res;
}int Lucas(long long a, long long b, int p) {if (a < p && b < p) return C(a, b, p); //终止条件return (long long)C(a % p, b % p, p) * Lucas(a / p, b / p, p) % p;
}
(三)
题目要求:
C n k = ? C_n^k=? Cnk=?
此处不模上数p了,且 n n n和 k k k的数据范围在 1 0 4 10^4 104以内。
上式可以写成,
C n k = n ! k ! ⋅ ( n − k ) ! C_n^k=\frac{n!}{k!\cdot (n-k)!} Cnk=k!⋅(n−k)!n!
考虑任意一个数 a a a的阶乘 a ! a! a!的分解质因子,
a ! = p 1 α 1 ⋅ p 2 α 2 ⋯ p k α k a!=p_1^{\alpha_1}\cdot p_2^{\alpha_2}\cdots p_k^{\alpha_k} a!=p1α1⋅p2α2⋯pkαk
对于 α i \alpha_i αi,其中 0 ≤ i ≤ k 0\leq i \leq k 0≤i≤k,可以通过如下式快速计算,
α i = ⌊ a p i ⌋ + ⌊ a p i 2 ⌋ + ⌊ a p i 3 ⌋ + ⋯ \alpha_i=\lfloor \frac{a}{p_i} \rfloor + \lfloor \frac{a}{p_i^2} \rfloor + \lfloor \frac{a}{p_i^3} \rfloor + \cdots αi=⌊pia⌋+⌊pi2a⌋+⌊pi3a⌋+⋯
那么,可以快速求解出 C n k C_n^k Cnk的分解质因子,然后利用高精度乘法将它们相乘即可。
代码如下,
#include <iostream>
#include <vector>using namespace std;const int N = 5010;
int primes[N], cnt;
bool st[N];
int sum[N];void get_primes(int n) {//求n以内的质数for (int i = 2; i <= n; ++i) {if (!st[i]) {primes[cnt++] = i;}for (int j = 0; primes[j] <= n / i; ++j) {st[i * primes[j]] = true;if (i % primes[j] == 0) break;}}return;
}int get(int a, int p) {//求a!中质因子p的幂int res = 0;while (a) {res += a / p;a /= p;}return res;
}vector<int> mul(vector<int> a, int b) {vector<int> c;int t = 0;for (int i = 0; i < a.size() || t; ++i) {if (i < a.size()) {t = t + a[i] * b;}c.emplace_back(t % 10);t /= 10; }while (c.size() > 1 && c.back() == 0) {c.pop_back();}return c;
}int main() {int a, b;cin >> a >> b;get_primes(a);for (int i = 0; i < cnt; ++i) {int p = primes[i];sum[i] = get(a, p) - get(b, p) - get(a - b, p);}vector<int> res = {1};for (int i = 0; i < cnt; ++i) {int p = primes[i];for (int j = 0; j < sum[i]; ++j) {res = mul(res, p);}}for (int i = res.size() - 1; i >= 0; --i) {cout << res[i];}cout << endl;return 0;
}
2 模板
暂无。。。
3 工程化
暂无。。。
相关文章:

acwing算法基础之数学知识--求组合数进阶版
目录 1 基础知识2 模板3 工程化 1 基础知识 请明确如下关于取余的基本定理: 数a和数b的乘积模上p,等于数a模上p和数b模上p的乘积。即, ( a ⋅ b ) m o d p ( a m o d p ) ⋅ ( b m o d p ) (a \cdot b ) \ mod \ p (a \ mod \ p) \cdot …...

基础算法:大数除以除以13
基础算法:大数除以一个数 信息学奥赛:1175:除以13 时间限制: 1000 ms 内存限制: 65536 KB 【题目描述】 输入一个大于0的大整数N,长度不超过100位,要求输出其除以13得到的商和余数。 【输入】 一个大于0的大整数&…...

软件版本区分
引言 定义好版本号对于产品的版本发布与持续更新很重要但是对于版本怎么定义规则如何确定却是千差万别。具体应用可以结合自己目前的实际情况命名。另外对于商业软件有的产品号称是永远的Beta版持续不断地更新、优化迭代产品才有生命力。 ⭕ 软件版本周期 α、β、λ 常用来…...
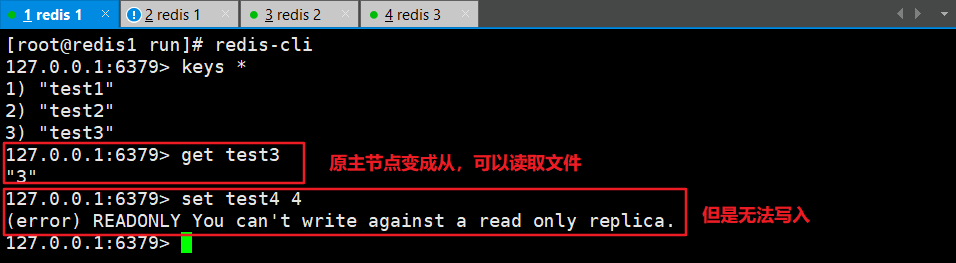
Redis高可用之主从复制及哨兵模式
一、Redis的主从复制 1.1 Redis主从复制定义 主从复制是redis实现高可用的基础,哨兵模式和集群都是在主从复制的基础之上实现高可用; 主从复制实现数据的多级备份,以及读写分离(主服务器负责写,从服务器只能读) 1.2 主从复制流…...
代理模式,dk动态代理,cglib动态代理
目录 一、代理模式1、生活中代理案例2、为什么要使用代理3、代理模式在Java中的应用4、什么是代理模式 二、代理的实现方式1、java中代理图示2、静态代理 三、动态代理1、概述2、JDK动态代理jdk动态代理原理分析 3、Cglib动态代理3.1 基本使用3.2 cglib基本原理 一、代理模式 …...
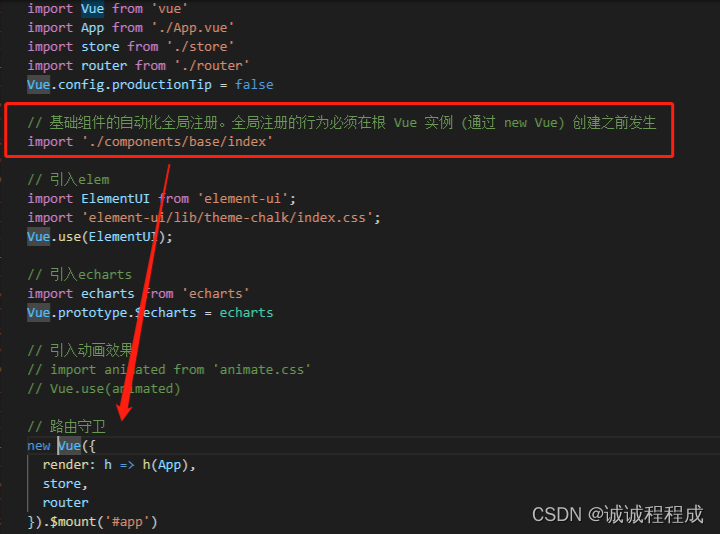
Vue2系列 -- 组件自动化全局注册(require.context)
参考官网:https://v2.cn.vuejs.org/v2/guide/components-registration.html 1 作用 省略 import 引入组件 省略 在main.js 中注册 实现自动化引入组件 2 自定义文件夹 在 src 下新建一个 components/base 文件夹,用于存放要自动注册的组件 3 在 base…...

【华为OD题库-038】支持优先级的对列-java
题目 实现一个支持优先级的队列,高优先级先出队列,同优先级时先进先出。 如果两个输入数据和优先级都相同,则后一个数据不入队列被丢弃。 队列存储的数据内容是一个 整数。 输入描述 一组待存入队列的数据(包含内容和优先级)。 输出描述 队列…...

python爱心代码高级
在Python中,我们可以使用matplotlib库来创建一个更高级的爱心图形。以下是一个示例: import matplotlib.pyplot as pltimport numpy as npx np.linspace(-2, 2, 1000)y1 np.sqrt(1-(abs(x)-1)**2)y2 -3*np.sqrt(1-(abs(x)/2)**0.5)fig, ax plt.subp…...
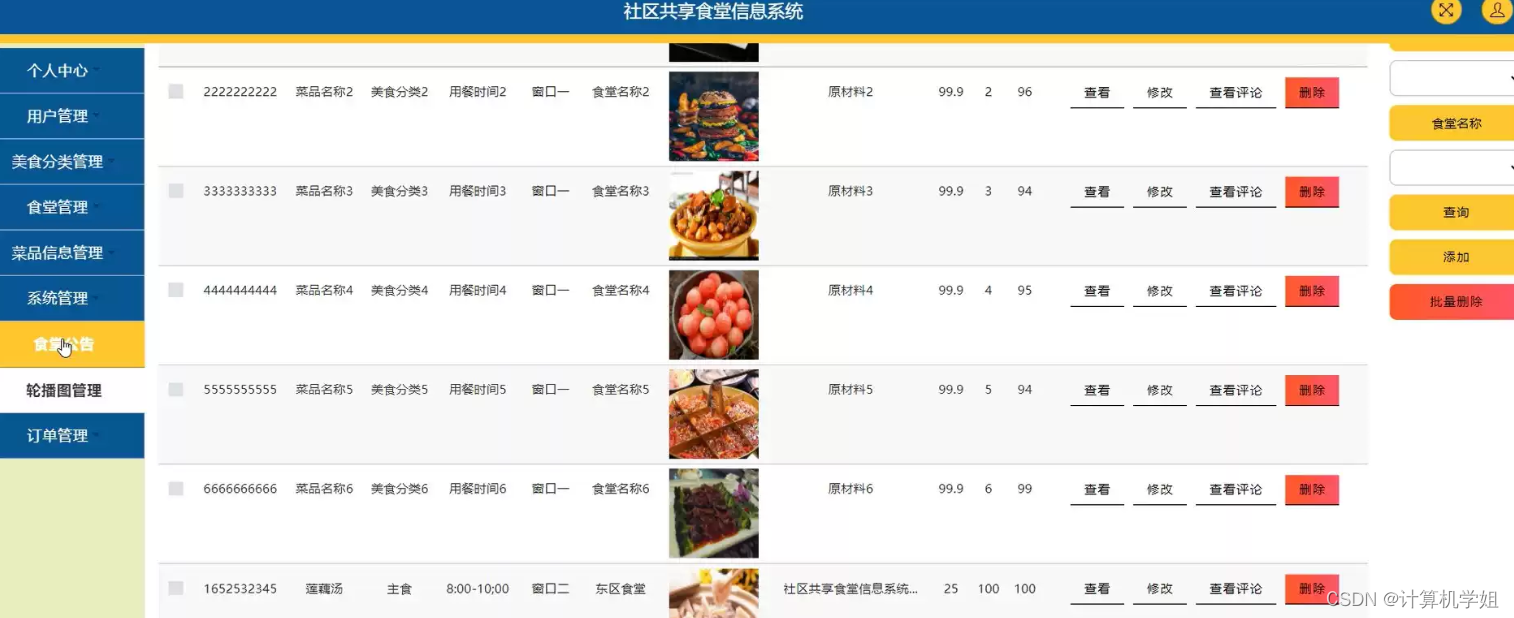
基于SSM+Vue的社区共享食堂管理系统
基于SSM的社区共享食堂管理系统的设计与实现~ 开发语言:Java数据库:MySQL技术:SpringMyBatisSpringMVC工具:IDEA/Ecilpse、Navicat、Maven 系统展示 主页 菜品详情 管理员界面 摘要 社区共享食堂管理系统是一种基于SSM…...

MYSQL基础知识之【修改数据,删除数据】
文章目录 前言MySQL UPDATE 查询使用PHP脚本更新数据 MySQL DELETE 语句从命令行中删除数据使用 PHP 脚本删除数据 后言 前言 hello world欢迎来到前端的新世界 😜当前文章系列专栏:Mysql 🐱👓博主在前端领域还有很多知识和技术…...

【机器学习】交叉验证 Cross-validation
交叉验证(CrossValidation)方法思想简介 以下简称交叉验证(Cross Validation)为CV.CV是用来验证分类器的性能一种统计分析方法,基本思想是把在某种意义下将原始数据(dataset)进行分组,一部分做为训练集(train set),另一部分做为验证集(validation set),首先用训练集对分类器进…...
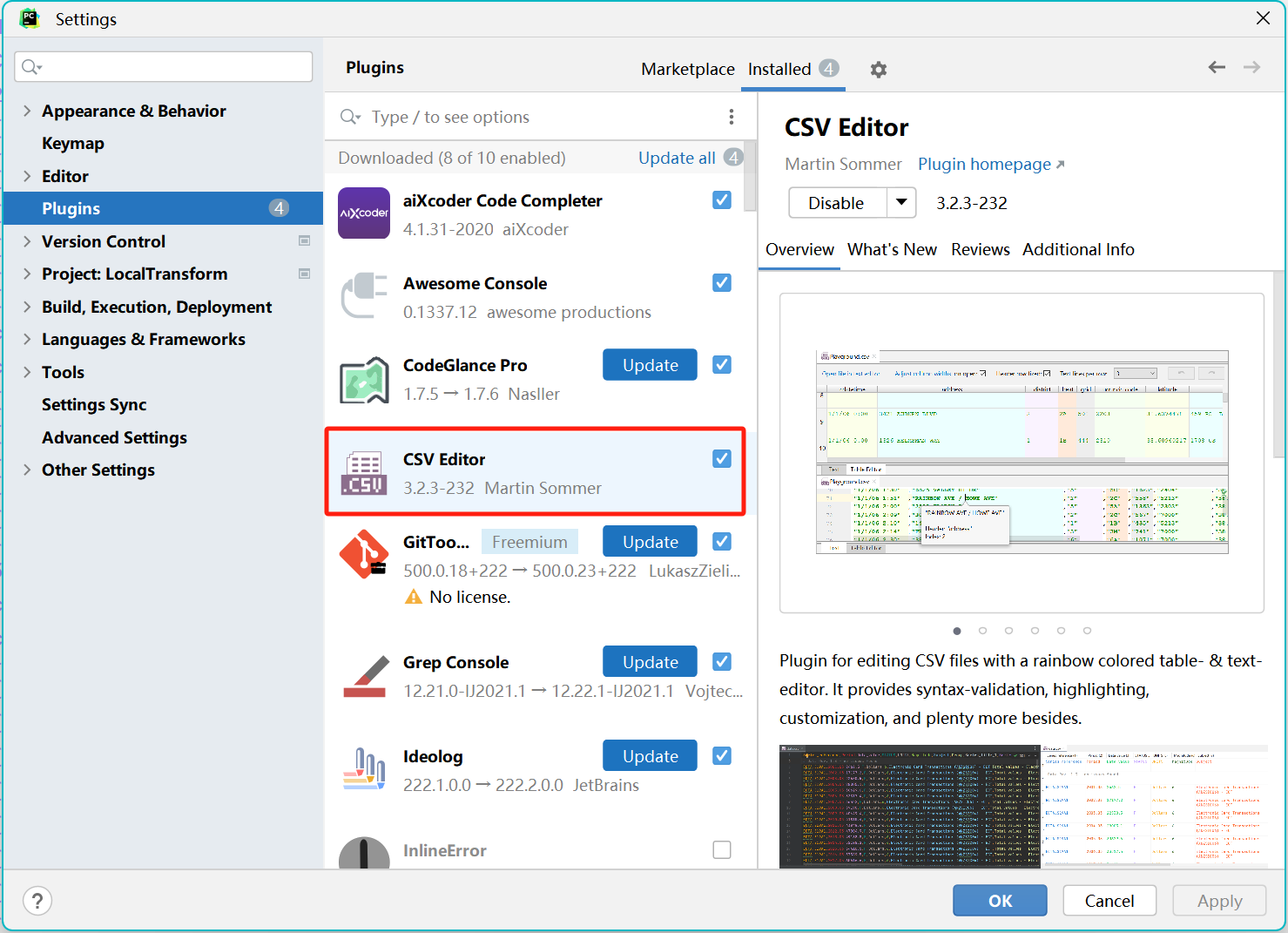
Pycharm修改文件默认打开方式 + CSV Editor插件使用
1、File —> Settings —> Editor —> File Types 然后将*csv添加到最上面 在plugins中下载插件,CSV Editor 备注:不在上一步的“File Types”中将*.csv设置为CSV格式,插件是不起作用的 就可以使用了...
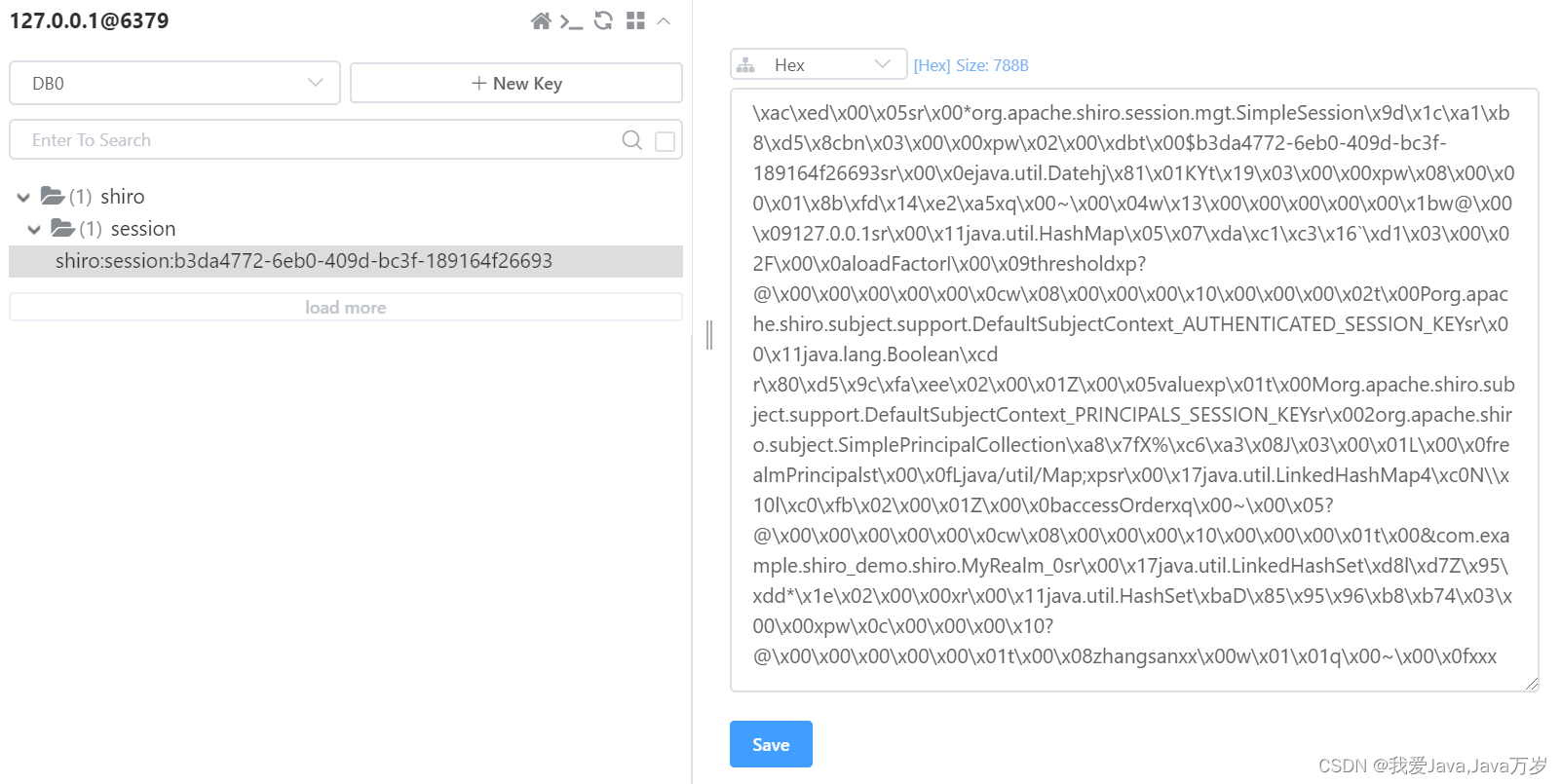
shiro整合redis
shiro整合redis 前言:shiro默认的session是存储在jvm内存中的,这样会导致java服务内存占用更大以及一旦服务器宕机或者版本迭代需要重启服务时,缓存中的数据不能恢复,导致用户需要重新登录认证,体验很差。因此利用第三…...
——@BuilderParam装饰器)
HarmonyOS(七)——@BuilderParam装饰器
前言: 前面我们认识了Builder装饰器:自定义构建函数,今天我们继续认识下一个装饰器——BuilderParam装饰器。 当开发者创建了自定义组件,并想对该组件添加特定功能时,例如在自定义组件中添加一个点击跳转操作。若直接…...
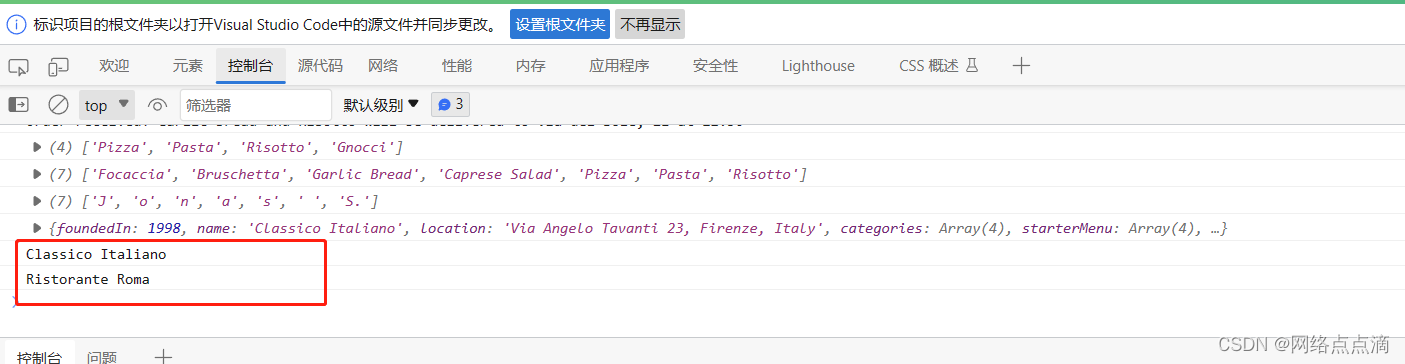
展开运算符(...)
假如我们有一个数组: const arr [7,8,9];● 我们如果想要数组中的元素,我们必须一个一个手动的去获取,如下: const arr [7,8,9]; const badNewArr [5, 6, arr[0], arr[1],arr[2]]; console.log(badNewArr);● 但是通过展开运…...
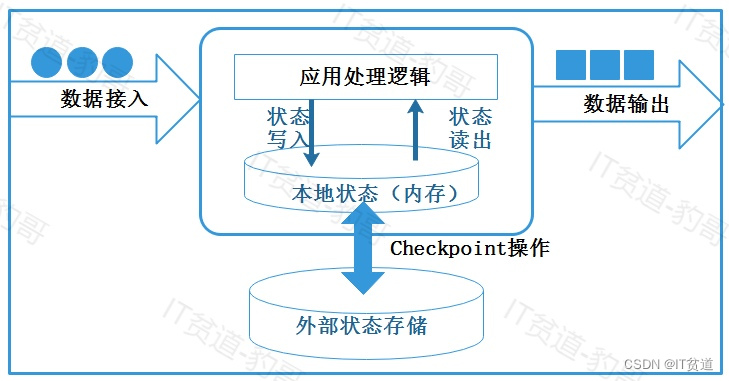
Apache Flink(二):数据架构演变
🏡 个人主页:IT贫道_大数据OLAP体系技术栈,Apache Doris,Clickhouse 技术-CSDN博客 🚩 私聊博主:加入大数据技术讨论群聊,获取更多大数据资料。 🔔 博主个人B栈地址:豹哥教你大数据的个人空间-豹…...
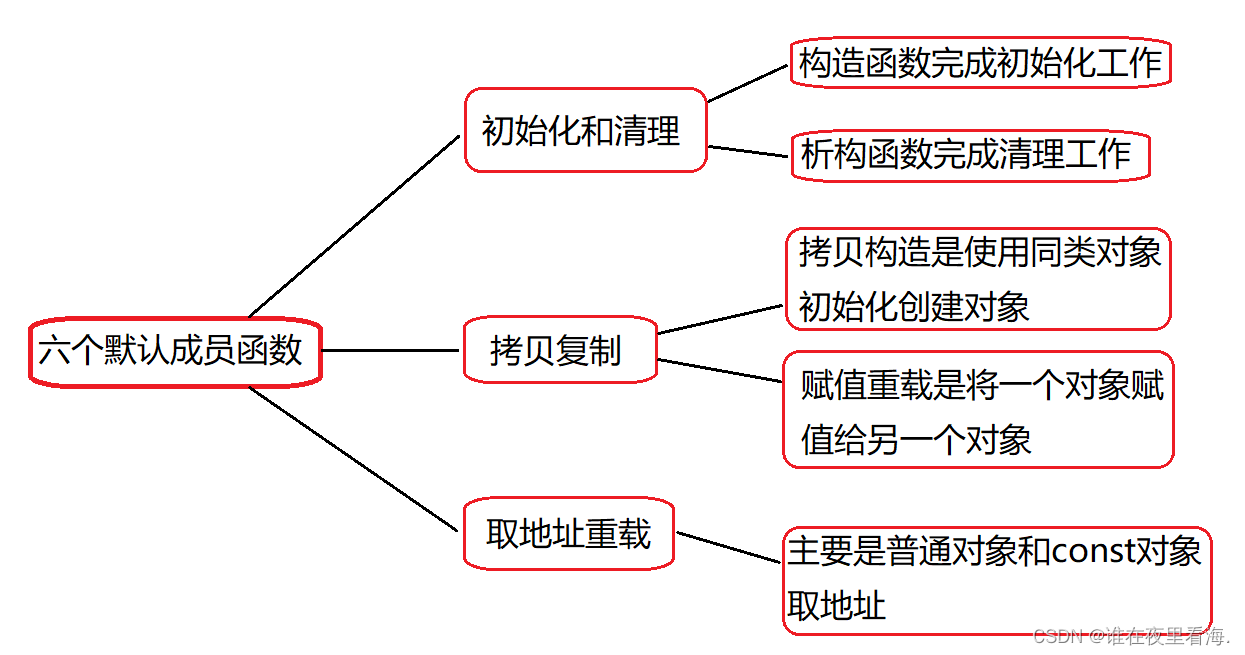
【C++】类与对象(中)
一、类的默认成员函数 如果一个类中什么成员都没有,简称为空类。 空类中真的什么都没有吗?并不是,任何类在什么都不写时,编译器会自动生成以下6个默认成员函数。 默认成员函数:用户没有显式实现,编译器会自…...

webshell之无扩展免杀
1.php加密 这里是利用phpjiami网站进行加密,进而达到加密效果 加密前: 查杀效果 可以看到这里D某和某狗都查杀 里用php加密后效果 查杀效果 可以看到这里只有D某会显示加密脚本,而某狗直接绕过 2.dezend加密 可以看到dezend加密的特征还是…...

用 VirtualBox 安装 OpenWrt 等 Linux 系统,无法启动的解决办法
用 VirtualBox 安装 OpenWrt 等 Linux 系统,无法启动的解决办法 最近新买了台联想小新 Pro 14 2023 锐龙版,因为有 32GB 的运行内存,所以想安装虚拟机以充分发挥。一开始使用 Hyper-V 来安装可以正常使用,但是后面想使用 Virtual…...

Windows下搭建Tomcat HTTP服务,发布公网远程访问
文章目录 前言1.本地Tomcat网页搭建1.1 Tomcat安装1.2 配置环境变量1.3 环境配置1.4 Tomcat运行测试1.5 Cpolar安装和注册 2.本地网页发布2.1.Cpolar云端设置2.2 Cpolar本地设置 3.公网访问测试4.结语 前言 Tomcat作为一个轻量级的服务器,不仅名字很有趣࿰…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...

Vue 3 + WebSocket 实战:公司通知实时推送功能详解
📢 Vue 3 WebSocket 实战:公司通知实时推送功能详解 📌 收藏 点赞 关注,项目中要用到推送功能时就不怕找不到了! 实时通知是企业系统中常见的功能,比如:管理员发布通知后,所有用户…...

【免费数据】2005-2019年我国272个地级市的旅游竞争力多指标数据(33个指标)
旅游业是一个城市的重要产业构成。旅游竞争力是一个城市竞争力的重要构成部分。一个城市的旅游竞争力反映了其在旅游市场竞争中的比较优势。 今日我们分享的是2005-2019年我国272个地级市的旅游竞争力多指标数据!该数据集源自2025年4月发表于《地理学报》的论文成果…...

goreplay
1.github地址 https://github.com/buger/goreplay 2.简单介绍 GoReplay 是一个开源的网络监控工具,可以记录用户的实时流量并将其用于镜像、负载测试、监控和详细分析。 3.出现背景 随着应用程序的增长,测试它所需的工作量也会呈指数级增长。GoRepl…...

拟合问题处理
在机器学习中,核心任务通常围绕模型训练和性能提升展开,但你提到的 “优化训练数据解决过拟合” 和 “提升泛化性能解决欠拟合” 需要结合更准确的概念进行梳理。以下是对机器学习核心任务的系统复习和修正: 一、机器学习的核心任务框架 机…...
