数据结构与算法复习笔记
1.数据结构基本概念
数据结构: 它是研究计算机数据间关系,包括数据的逻辑结构和存储结构及其操作。
数据(Data):数据即信息的载体,是能够输入到计算机中并且能被计算机识别、存储和处理的符号总称。
数据元素(Data Element):数据元素是数据的基本单位,又称之为记录(Record)。一般,数据元素由若干基本项(或称字段、域、属性)组成。
1.1.数据的逻辑结构
数据的逻辑结构表示数据运算之间的抽象关系。按每个元素可能具有的直接前趋数和直接后继数将逻辑结构分为“线性结构”和“非线性结构”两大类。
线性结构:

一个对一个,如线性表、栈、队列
树形结构:
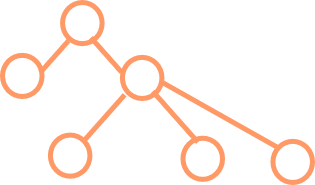
一个对多个,如树。
图状结构
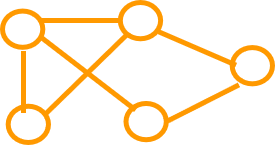
多个对多个
此外还有集合:

数据元素间除“同属于一个集合”外,无其它关系。
1.2.数据的存储结构
存储结构:逻辑结构在计算机中的具体实现方法。
存储结构是通过计算机语言所编制的程序来实现的,因而是依赖于具体的计算机语言的。
顺序存储(Sequential Storage):
将数据结构中各元素按照其逻辑顺序存放于存储器一片连续的存储空间中。
如c语言的一维数组,如表 L=(a1,a2,……,an)的顺序结构


链式存储(重点)
将数据结构中各元素分布到存储器的不同点,用地址(或链指针)方式建立它们之间的联系。

数据结构中元素之间的关系在计算机内部很大程度上是通过地址或指针来建立的。
索引存储
在存储数据的同时,建立一个附加的索引表,即索引存储结构=数据文件+索引表。

散列存储:
根据数据元素的特殊字段(称为关键字key),计算数据元素的存放地址,然后数据元素按地址存放

2.线性表
线性表是包含若干数据元素的一个线性序列
记为: L=(a0, … ai-1, ai, ai+1 … an-1)
L为表名,ai (0≤i≤n-1)为数据元素;
n为表长,n>0 时,线性表L为非空表,否则为空表。
线性表L可用二元组形式描述:
L= (D,R)
即线性表L包含数据元素集合D和关系集合R
D={ai | ai∈datatype ,i=0,1,2, ∙∙∙∙∙∙∙∙∙n-1 ,n≥0}R={<ai , ai+1> | ai , ai+1∈D, 0≤i≤n-2}
- 关系符<ai, ai+1>在这里称为有序对
- 表示任意相邻的两个元素之间的一种先后次序关系
- ai是ai+1的直接前驱, ai+1是ai的直接后继
线性表的特征:
- 对非空表,a0是表头,无前驱;
- an-1是表尾,无后继;
- 其它的每个元素ai有且仅有一个直接前驱ai-1和一个直接后继ai+1。
线性表包括顺序表和链表,其中链表又包括单链和双链。线性表具体分类如下:

设有一个顺序表L={1,2,3,4,5,6}; 他们的关系如图:
使用二元组描述L=(D,R),则
D={1 , 2 , 3 , 4 , 5 , 6}(n=6)R={<1,2> , <2,3> , <3,4> , <4,5> , <5,6>}
2.1. 顺序表
2.1.1.顺序存储结构的表示
若将线性表L=(a0,a1, ……,an-1)中的各元素依次存储于计算机一片连续的存储空间。
设Loc(ai)为ai的地址,Loc(a0)=b,每个元素占d个单元 则:Loc(ai)=b+i*d

2.1.2.顺序存储结构的特点
- 逻辑上相邻的元素 ai, ai+1,其存储位置也是相邻的
- 对数据元素ai的存取为随机存取或按地址存取
- 存储密度高,存储密度D=(数据结构中元素所占存储空间)/(整个数据结构所占空间)
- 顺序存储结构的不足:
对表的插入和删除等运算的时间复杂度较差
2.1.3.顺序存储的C语言实现
在C语言中,可借助于一维数组类型来描述线性表的顺序存储结构:
#define N 100
typedef int data_t;
typedef struct
{ data_t data[N]; //表的存储空间int last;
} sqlist, *sqlink;

2.1.4.线性表的基本运算
设线性表 L=(a0,a1, ……,an-1),对 L的基本运算有:
1)建立一个空表:list_create(L)
2)置空表:list_clear(L)
3)判断表是否为空:list_empty (L)。若表为空,返回值为1 , 否则返回 0
4)求表长:length (L)
5)取表中某个元素:GetList(L , i ), 即ai。要求0≤i≤length(L)-1
6)定位运算:Locate(L,x)。确定元素x在表L中的位置(或序号)
L o c a t e ( L , x ) = { i , 当元素 x = a i ∈ L , 且 a i 是第一个与 x 相等时 − 1 x 不属于 L 时 Locate(L,x) = \begin{cases} i , &当元素x=ai∈L,且ai是第一个与x相等时 \\ -1 & x不属于L时 \\ \end{cases} Locate(L,x)={i,−1当元素x=ai∈L,且ai是第一个与x相等时x不属于L时
定位:确定给定元素x在表L中第一次出现的位置(或序号)。即实现Locate(L,x)。算法对应的存储结构如图所示。

7)插入:
Insert(L,x,i)。将元素x插入到表L中第i个元素ai之前,且表长+1。
插入前: (a0,a1,—,ai-1,ai,ai+1-------,an-1) 0≤i≤n,i=n时,x插入表尾
插入后: (a0,a1,—,ai-1, x, ai,ai+1-------,an-1)
插入算法思路:若表存在空闲空间,且参数i满足:0≤i≤L->last+1,则可进行正常插入。插入前,将表中(L->data[L->last]~L->data[i])部分顺序下移一个位置,然后将x插入L->data[i]处即可。算法对应的表结构。

8)删除:
Delete(L,i)。删除表L中第i个元素ai,且表长减1, 要求0≤i≤n-1。
删除前: (a0,a1,—,ai-1,ai,ai+1-------,an-1)
删除后: (a0,a1,—,ai-1,ai+1-------,an)
删除:将表中第i个元素ai从表中删除,即实现DeleteSqlist(L, i)。
算法思路: 若参数i满足:0≤i≤L->last, 将表中L->data[i+1]∽L->data[L->last] 部分顺序向上移动一个位置,覆盖L->data[i]。

2.1.5.顺序表缺点
线性表的顺序存储结构有存储密度高及能够随机存取等优点,但存在以下不足:
(1)要求系统提供一片较大的连续存储空间。
(2)插入、删除等运算耗时,且存在元素在存储器中成片移动的现象;
2.2. 链表
链表主要学习单链表
2.2.1.线性表的链式存储结构:
将线性表L=(a0,a1,……,an-1)中各元素分布在存储器的不同存储块,称为结点,通过地址或指针建立元素之间的联系

结点的data域存放数据元素ai,而next域是一个指针,指向ai的直接后继ai+1所在的结点。

2.2.2.单链表的C语言实现
1.创建结构体
typedef struct node{ data_t data; //结点的数据域//struct node *next; //结点的后继指针域//}listnode, *linklist;

设p指向链表中结点ai

获取ai,写作:p->data;
而取ai+1,写作:p->next->data
若指针p的值为NULL,则它不指向任何结点, 此时取p->data或p->next是错误的。
可调用C语言中malloc()函数向系统申请结点的存储空间
linklist p;
p = (linklist)malloc(sizeof(listnode));
则创建一个类型为linklist的结点,且该结点的地址已存入指针变量p中:

2.建立单链表
依次读入表L=(a0,…,an-1)中每一元素ai(假设为整型),若ai≠结束符(-1),则为ai创建一结点,然后插入表尾,最后返回链表的头结点指针H。
设L=(2,4,8,-1),则建表过程如下:

链表的结构是动态形成的,即算法运行前,表结构是不存在的
3.链表查找
1)按序号查找:实现GetLinklist(h, i)运算。
算法思路:从链表的a0起,判断是否为第i结点,若是则返回该结点的指针,否则查找下一结点,依次类推。
2)按值查找(定位) : 即实现Locate(h, x)。
算法思路:从链表结点a0起,依次判断某结点是否等于x,若是,则返回该结点的地址,若不是,则查找下一结点a1,依次类推。若表中不存在x,则返回NULL。
4.链表的插入
即实现InsertLinklist(h, x, i,)。将x插入表中结点ai之前的情况。
算法思路:调用算法GetLinklist(h, i-1),获取结点ai-1的指针p(ai 之前驱),然后申请一个q结点,存入x,并将其插入p指向的结点之后。

5.链表的删除
即实现DeleteLinklist(h, i), 算法对应的链表结构如图所示。
算法思路:同插入法,先调用函数GetLinklist(h, i-1),找到结点ai的前驱,然后将结点ai删除之。

2.2.3.设计算法,将单链表H倒置
算法思路:依次取原链表中各结点,将其作为新链表首结点插入H结点之后
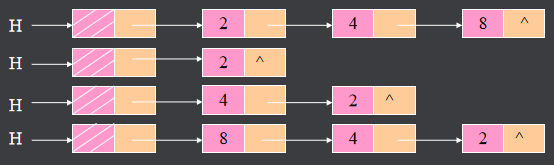
2.2.4.设计算法,求两节点之和
设结点data域为整型,求链表中相邻两结点data值之和为最大的第一结点的指针。
算法思路:设p,q 分别为链表中相邻两结点指针,求p->data+q->data为最大的那一组值,返回其相应的指针p即可

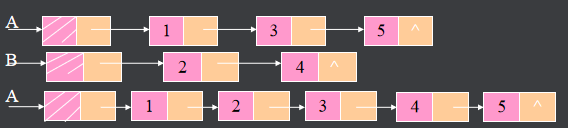
2.2.5.链表合并
设两单链表A、B按data值(设为整型)递增有序,将表A和B合并成一表A,且表A也按data值递增有序。
算法思路:设指针p、q分别指向表A和B中的结点,若p->data ≤q->data则p结点进入结果表,否则q结点进入结果表。
3.栈
栈是限制在一端进行插入操作和删除操作的线性表(俗称堆栈),允许进行操作的一端称为“栈顶”,另一固定端称为“栈底”,当栈中没有元素时称为“空栈”。
特点 :后进先出(LIFO)。

3.1.顺序栈
它是顺序表的一种,具有顺序表同样的存储结构,由数组定义,配合用数组下标表示的栈顶指针top(相对指针)完成各种操作。
3.1.1.C语言实现
1.创建结构体
typedef int data_t ; /*定义栈中数据元素的数据类型*/
typedef struct
{ data_t *data ; /*用指针指向栈的存储空间*/int maxlen; /*当前栈的最大元素个数*/int top ; /*指示栈顶位置(数组下标)的变量*/} sqstack; /*顺序栈类型定义*/
2.创建栈
sqstack *stack_create (int len)
{
sqstack *ss;
ss = (seqstack *)malloc(sizeof(sqstack));
ss->data = (data_t *)malloc(sizeof(data_t) * len);
ss->top = -1;
ss->maxlen = len;
return ss;
}

3.清空栈
stack _clear(sqstack *s)
{s-> top = -1 ;
} //判断栈是否空 :
int stack_empty (sqstack *s)
{ return (s->top == -1 ? 1 : 0);
}
4.进栈
void stack_push (sqstack *s , data_t x)
{ if (s->top = = N - 1){printf ( “overflow !\n”) ; return ;}else { s->top ++ ;s->data[s->top] = x ;}return ;
}
5.出栈
datatype stack_pop(sqstack *s)
{s->top--;return (s->data[s->top+1]);
} //取栈顶元素:
datatype get_top(sqstack *s)
{return (s->data[s->top]);
}
3.2.链式栈
C语言实现过程如下:
插入操作和删除操作均在链表头部进行,链表尾部就是栈底,栈顶指针就是头指针。
1.创建结构体
ypedef int data_t ; /*定义栈中数据元素数据类型*/
typedef struct node_t {data_t data ; /*数据域*/struct node_t *next ; /*链接指针域*/
} linkstack_t ; /*链栈类型定义*/
2.创建空栈
linkstack_t *CreateLinkstack() { linkstack_t *top;top = (linkstack_t *)malloc(sizeof(linkstack_t));top->next = NULL;return top;
}//判断是否空栈 :
int EmptyStack (linkstack_t *top)
{ return (top->next == NULL ? 1 : 0);
}
3.入栈
void PushStack(linkstack_t *top, data_t x)
{
linkstack_t *p ;
p = (linkstack_t *)malloc ( sizeof (linkstack_t) ) ;
p->data = x ;
p->next = top->next;
top->next = p;
return;
}
4.队列
队列是限制在两端进行插入操作和删除操作的线性表
- 允许进行存入操作的一端称为“队尾”
- 允许进行删除操作的一端称为“队头”
- 当线性表中没有元素时,称为“空队”
- 特点 :先进先出(FIFO)

front指向队头元素的位置; rear指向队尾元素的下一个位置。 - 在队列操作过程中,为了提高效率,以调整指针代替队列元素的移动,并将数组作为循环队列的操作空间。
- 为区别空队和满队,满队元素个数比数组元素个数少一个。
4.1.顺序队列
C语言实现:
1.创建结构体
typedef int data_t ; /*定义队列中数据元素的数据类型*/
#define N 64 /*定义队列的容量*/
typedef struct {data_t data[N] ; /*用数组作为队列的储存空间*/int front, rear ; /*指示队头位置和队尾位置的指针*/
} sequeue_t ; /*顺序队列类型定义*/
2.创建空队列
sequeue_t *CreateQueue ()
{ sequeue_t *sq = (sequeue_t *)malloc(sizeof(sequeue_t));sq->front = sq->rear = maxsize -1;return sq;
}
//判断队列空:
int EmptyQueue (sequeue_t *sq) {return (sq->front = = sq->rear) ;
}
3.入队
将新数据元素x插入到队列的尾部
void EnQueue (sequeue_t *sq , data_t x)
{sq->data[sq->rear] = x ; sq->rear = (sq->rear + 1) % N ; return ;
}
4.2.链式队列
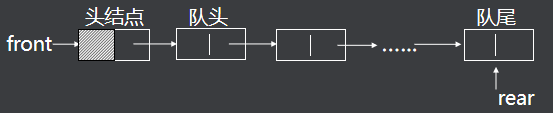
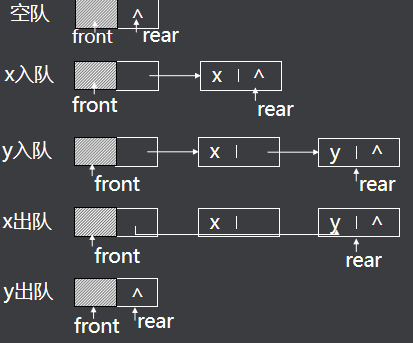
C语言实现:
1.创建结构体
插入操作在队尾进行,删除操作在队头进行,由队头指针和队尾指针控制队列的操作。
typedef int data_t;
typedef struct node_t
{ data_t data ; struct node_t *next; } linknode_t, *linklist_t; typedef struct{ linklist_t front, rear; } linkqueue_t;
2.创建空队列
linkqueue_t *CreateQueue()
{ linkqueue_t *lq = (linkqueue_t *)malloc(sizeof(linkqueue_t));lq->front = lq->rear = (linklist_t)malloc(sizeof(linknode_t));lq->front->next = NULL ; /*置空队*/return lq; /*返回队列指针*/
}//判断队列空 :
int EmptyQueue(linkqueue_t *lq) { return ( lq->front = = lq->rear) ;
}
3.入队
void EnQueue (linkqueue_t *lq, data_t x)
{lq->rear->next (linklist_t)malloc(sizeof(linknode_t)) ; lq->rear = lq->rear->next; /*修改队尾指针*/lq->rear->data = x ; /*新数据存入新节点*/lq->rear->next = NULL ; /*新节点为队尾*/return;
}
4.出队
data_t DeQueue(linkqueue_t *lq)
{data_t x;linklist_t p; /*定义一个指向队头结点的辅助指针*/p = lq->front->next ; /*将它指向队头结点*/lq->front->next = p->next ; /*删除原先队头结点x = p->data;free(p) ; /*释放原队头结点*/if (lq->front->next == NULL) lq->rear = lq->front;return x;
}
5.树和二叉树
5.1.树的相关概念
树(Tree)是n(n≥0)个节点的有限集合T,它满足两个条件 :
- 有且仅有一个特定的称为根(Root)的节点。
- 其余的节点可以分为m(m≥0)个互不相交的有限集合T1、T2、……、Tm,其中每一个集合又是一棵树,并称为其根的子树。
表示方法 :树形表示法、目录表示法。

度: 一个节点的子树的个数称为该节点的度数,一棵树的度数是指该树中节点的最大度数。 - 度数为零的节点称为树叶或终端节点
- 度数不为零的节点称为分支节点
- 除根节点外的分支节点称为内部节点。

路径: 一个节点系列k1,k2, ……,ki,ki+1, ……,kj,并满足ki是ki+1的父节点,就称为一条从k1到kj的路径 - 路径的长度为j-1,即路径中的边数。
- 路径中前面的节点是后面节点的祖先,后面节点是前面节点的子孙。
- 节点的层数等于父节点的层数加一,根节点的层数定义为一。树中节点层数的最大值称为该树的高度或深度。
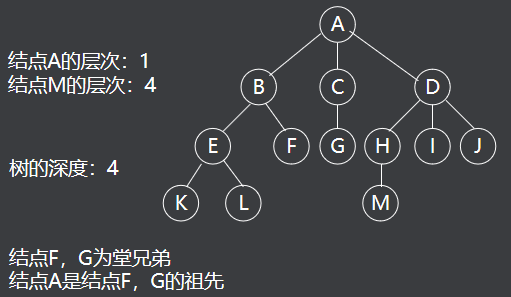
有序树: 若树中每个节点的各个子树的排列为从左到右,不能交换,即兄弟之间是有序的,则该树称为有序树。
森林: m(m≥0)棵互不相交的树的集合称为森林。
树去掉根节点就成为森林,森林加上一个新的根节点就成为树
树的逻辑结构 :
树中任何节点都可以有零个或多个直接后继节点(子节点),但至多只有一个直接前趋节点(父节点),根节点没有前趋节点,叶节点没有后继节点。
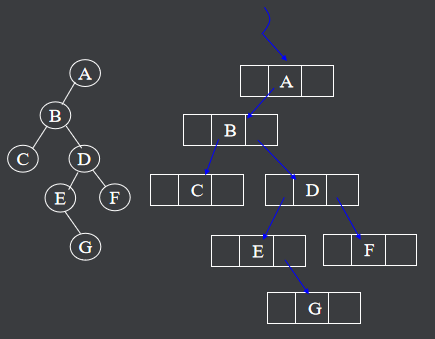
5.2.二叉树
二叉树是n(n≥0)个节点的有限集合,可以是空集(n=0)
也可以是由一个根节点以及两棵互不相交的、分别称为左子树和右子树的二叉树组成。
严格区分左孩子和右孩子,即使只有一个子节点也要区分左右。
5.2.1.二叉树的性质
二叉树第i(i≥1)层上的节点最多为2i-1个。
深度为k(k≥1)的二叉树最多有2k-1个节点。
满二叉树 : 深度为k(k≥1)时有2k-1个节点的二叉树。
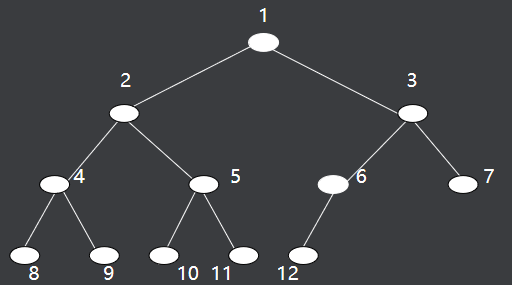
完全二叉树 : 只有最下面两层有度数小于2的节点,且最下面一层的叶节点集中在最左边的若干位置上。
具有n个节点的完全二叉树的深度为
(log2n)+1或 log2(n+1)。
顺序存储结构 : 完全二叉树节点的编号方法是从上到下,从左到右,根节点为1号节点。设完全二叉树的节点数为n,某节点编号为i。
- 当i>1(不是根节点)时,有父节点,其编号为i/2;
- 当2i≤n时,有左孩子,其编号为2i ,否则没有左孩子,本身是叶节点;
- 当2i+1≤n时,有右孩子,其编号为2i+1 ,否则没有右孩子;
- 当i为奇数且不为1时,有左兄弟,其编号为i-1,否则没有左兄弟;
- 当i为偶数且小于n时,有右兄弟,其编号为i+1,否则没有右兄弟;
有n个节点的完全二叉树可以用有n+1个元素的数组进行顺序存储,节点号和数组下标一一对应,下标为零的元素不用。
利用以上特性,可以从下标获得节点的逻辑关系。不完全二叉树通过添加虚节点构成完全二叉树,然后用数组存储,这要浪费一些存储空间。
5.2.2.二叉树的顺序存储

5.2.2.二叉树的链式存储
C语言实现创建结构体
typedef int data_t ;
typedef struct node_t;
{data_t data ; struct node_t *lchild ,*rchild ;
} bitree_t ;
bitree_t *root ;
二叉树由根节点指针决定。
5.2.3.二叉树的遍历运算
遍历 : 沿某条搜索路径周游二叉树,对树中的每一个节点访问一次且仅访问一次。
二叉树是非线性结构,每个结点有两个后继,则存在如何遍历即按什么样的搜索路径进行遍历的问题。
由于二叉树的递归性质,遍历算法也是递归的。三种基本的遍历算法如下 :
- 先访问树根,再访问左子树,最后访问右子树;
- 先访问左子树,再访问树根,最后访问右子树;
- 先访问左子树,再访问右子树,最后访问树根;
先序遍历算法
void PREORDER ( bitree *r)
{if ( r = = NULL ) return ; //空树返回printf ( “ %c ”,r->data ); //先访问当前结点PREORDER( r->lchild ); //再访问该结点的左子树PREORDER( r->rchild ); //最后访问该结点右子树
}
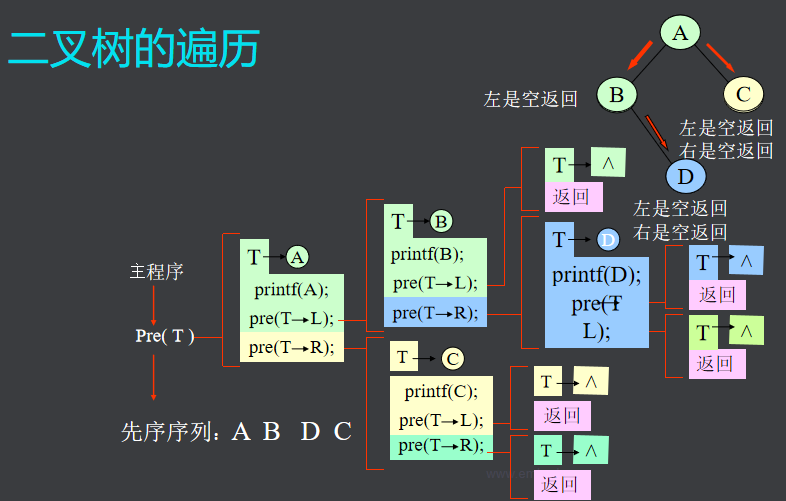
中序遍历算法
若二叉树为空树,则空操作;否则中序遍历左子树。
当访问根结点,中序遍历右子树。
void INORDER ( bitree *r)
{if ( r = = NULL ) return ; //空树返回INORDER( r->lchild ); //先访问该结点的左子树printf ( “ %c ”,r->data ); //再访问当前结点INORDER( r->rchild ); //最后访问该结点右子树
}
后序遍历算法
若二叉树为空树,则空操作;否则后序遍历左子树
当访问根结点,后序遍历右子树。
void POSTORDER ( bitree *r)
{if ( r = = NULL ) return ; //空树返回POSTORDER( r->lchild ); //先访问该结点的左子树POSTORDER( r->rchild ); //再访问该结点右子树printf ( “ %c ”,r->data ); //最后访问当前结点
}
遍历的路径相同,均为从根节点出发,逆时针沿二叉树的外缘移动,每个节点均经过三次。按不同的次序访问可得不同的访问系列,每个节点有它的逻辑前趋(父节点)和逻辑后继(子节点),也有它的遍历前趋和遍历后继(要指明遍历方式)。
按编号遍历算法 :
NOORDER ( bitree *r) /*按编号顺序遍历算法*/
{int front, rear;bitree *Q[N];if ( r == NULL ) return ; /*空树返回*/for (rear=1;rear<N; rear++) Q[rear] = NULL ;front = rear = 1; Q[rear] = r;while ( Q[front] != NULL ) { /*以下部分算法由学生完成设计*//*访问当前出队节点*//*若左孩子存在则左孩子入队*//*若有孩子存在则右孩子入队*//* front向后移动*/}
}
6.查找算法
查找:
设记录表L=(R1 R2……Rn),其中Ri(l≤i≤n)为记录,对给定的某个值k,在表L中确定key=k的记录的过程,称为查找。
若表L中存在一个记录Ri的key=k,记为Ri.key=k,则查找成功,返回该记录在表L中的序号i(或Ri 的地址),否则(查找失败)返回0(或空地址Null)。
6.1.平均查找长度
对查找算法,主要分析其T(n)。查找过程是key的比较过程,时间主要耗费在各记录的key与给定k值的比较上。比较次数越多,算法效率越差(即T(n)量级越高),故用“比较次数”刻画算法的T(n)。
一般以“平均查找长度”来衡量T(n)。
平均查找长度ASL(Average Search Length):对给定k,查找表L中记录比较次数的期望值(或平均值),即:

Pi为查找Ri的概率。等概率情况下Pi=1/n;Ci为查找Ri时key的比较次数(或查找次数)。
6.2.顺序表的查找
顺序表,是将表中记录(R1 R2……Rn)按其序号存储于一维数组空间
记录Ri的类型描述如下:
typedef struct
{ keytype key; //记录key//…… //记录其他项//
} Retype;
顺序表类型描述如下:
#define maxn 1024 //表最大长度//
typedef struct
{ Retype data[maxn]; //顺序表空间//int len; //当前表长,表空时len=0//
} sqlist;
若说明:sqlist r,则(r.data[1],……,r.data[r.len])为记录表(R1……Rn), Ri.key为r.data[i].key, r.data[0]称为监视哨,为算法设计方便所设。
算法思路: 设给定值为k,在表(R1 R2……Rn)中,从Rn开始,查找key=k的记录。
int sqsearch(sqlist r, keytype k)
{ int i;r.data[0].key = k; //k存入监视哨//i = r.len; //取表长//while(r.data[i].key != k) i--; return (i);
}
设Ci(1≤i≤n)为查找第i记录的key比较次数(或查找次数):
若r.data[n].key = k, Cn=1;若r.data[n-1].key = k, Cn-1=2;……若r.data[i].key = k, Ci=n-i+1;……若r.data[1].key = k, C1=n
故ASL = O(n)。而查找失败时,查找次数等于n+l,同样为O(n)。
- 对查找算法,若ASL=O(n),则效率是很低的,意味着查找某记录几乎要扫描整个表,当表长n很大时,会令人无法忍受。
6.3.折半查找算法
算法思路:
对给定值k,逐步确定待查记录所在区间,每次将搜索空间减少一半(折半),直到查找成功或失败为止。
设两个游标low、high,分别指向当前待查找表的上界(表头)和下界(表尾)。mid指向中间元素。
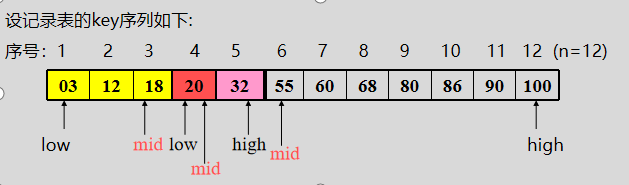
现查找k=20的记录。
再看查找失败的情况,设要查找k=85的记录。
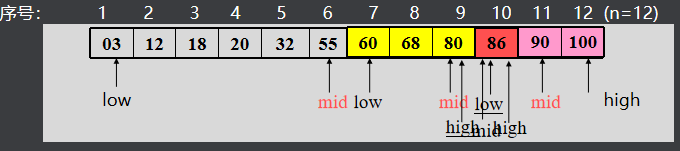
C语言实现如下:
int Binsearch(sqlist r, keytype k) //对有序表r折半查找的算法//
{ int low, high, mid; low = 1;high = r.len; while (low <= high) { mid = (low+high) / 2; if (k == r.data[mid].key) return (mid); if (k < r.data[mid].key) high = mid-1; else low = mid+1;} return(0);}
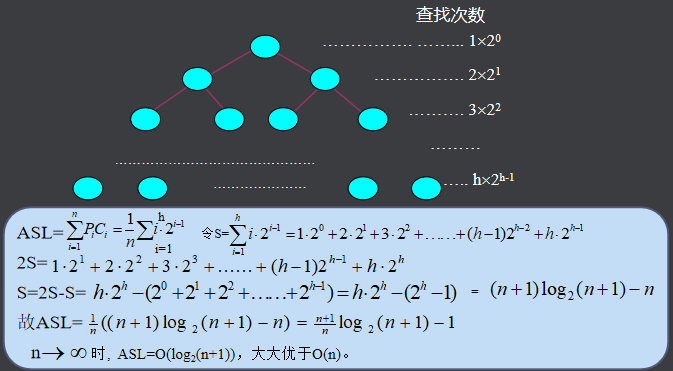
不失一般性,设表长n=2h-l,h=log2(n+1)。记录数n恰为一棵h层的满二叉树的结点数。得出表的判定树及各记录的查找次数如图所示。
6.4.分块查找算法
设记录表长为n,将表的n个记录分成b=[n/s]个块,每块s个记录(最后一块记录数可以少于s个),即:
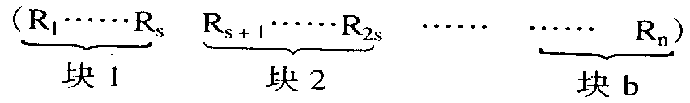
且表分块有序,即第i(1≤i≤b-1)块所有记录的key小于第i+1块中记录的key,但块内记录可以无序。
步骤:
- 建立索引
- 每块对应一索引项:
- 其中kmax为该块内记录的最大key;link为该块第一记录的序号(或指针)。


- 顺序、折半、分块查找和树表的查找中,其ASL的量级在O(n)~O(log2n)之间。
- 不论ASL在哪个量级,都与记录长度n有关。随着n的扩大,算法的效率会越来越低。
- ASL与n有关是因为记录在存储器中的存放是随机的,或者说记录的key与记录的存放地址无关,因而查找只能建立在key的“比较”基础上。
7.排序算法
稳定排序和非稳定排序
设文件f=(R1……Ri……Rj……Rn)中记录Ri、Rj(i≠j,i、j=1……n)的key相等,即Ki=Kj。
若在排序前Ri领先于Rj,排序后Ri仍领先于Rj,则称这种排序是稳定的,其含义是它没有破坏原本已有序的次序。
内排序和外排序
- 若待排文件f在计算机的内存储器中,且排序过程也在内存中进行,称这种排序为内排序。
- 若排序中的文件存入外存储器,排序过程借助于内外存数据交换(或归并)来完成,则称这种排序为外排序。
各种内排序方法可归纳为以下五类:
(1)插入排序
(2)交换排序
(3)选择排序
(4)归并排序
插入排序方法可归纳为以下五类:
(1) 直接插入排序
(2) 折半插入排序
(3) 链表插入排序
(4) Shell(希尔)排序
7.1.直接插入排序
设待排文件f=(R1 R2……Rn)相应的key集合为k={k1 k2……kn},
排序方法:
先将文件中的(R1)看成只含一个记录的有序子文件,然后从R2起,逐个将R2至Rn按key插入到当前有序子文件中,最后得到一个有序的文件。插入的过程上是一个key的比较过程,即每插入一个记录时,将其key与当前有序子表中的key进行比较,找到待插入记录的位置后,将其插入即可。
设文件记录的key集合k={50,36,66,76,95,12,25,36}

7.2.折半插入排序
排序算法的T(n)=O(n2),是内排序时耗最高的时间复杂度。
折半插入排序方法
先将(R[1])看成一个子文件,然后依次插入R[2]……R[n]。但在插入R[i]时,子表[R[1]……R[i-1]]已是有序的,查找R[i]在子表中的位置可按折半查找方法进行,从而降低key的比较次数。

7.3.链表插入排序
设待排序文件f=(R1 R2……Rn),对应的存储结构为单链表结构

链表插入排序实际上是一个对链表遍历的过程。先将表置为空表,然后依次扫描链表中每个结点,设其指针为p,搜索到p结点在当前子表的适当位置,将其插入。
设含4个记录的链表如图:

7.4.起泡排序

7.5.快速排序
设记录的key集合k={50,36,66,76,36,12,25,95},每次以集合中第一个key为基准的快速排序过程如下:

相关文章:

数据结构与算法复习笔记
1.数据结构基本概念 数据结构: 它是研究计算机数据间关系,包括数据的逻辑结构和存储结构及其操作。 数据(Data):数据即信息的载体,是能够输入到计算机中并且能被计算机识别、存储和处理的符号总称。 数据元素…...
关于微服务的思考
目录 什么是微服务 定义 特点 利弊 引入时机 需要哪些治理环节 从单体架构到微服务架构的演进 单体架构 集群和垂直化 SOA 微服务架构 如何实现微服务架构 服务拆分 主流微服务解决方案 基础设施 下一代微服务架构Service Mesh 什么是Service Mesh?…...
计算机毕业设计 基于Web的课程设计选题管理系统的设计与实现 Java实战项目 附源码+文档+视频讲解
博主介绍:✌从事软件开发10年之余,专注于Java技术领域、Python人工智能及数据挖掘、小程序项目开发和Android项目开发等。CSDN、掘金、华为云、InfoQ、阿里云等平台优质作者✌ 🍅文末获取源码联系🍅 👇🏻 精…...
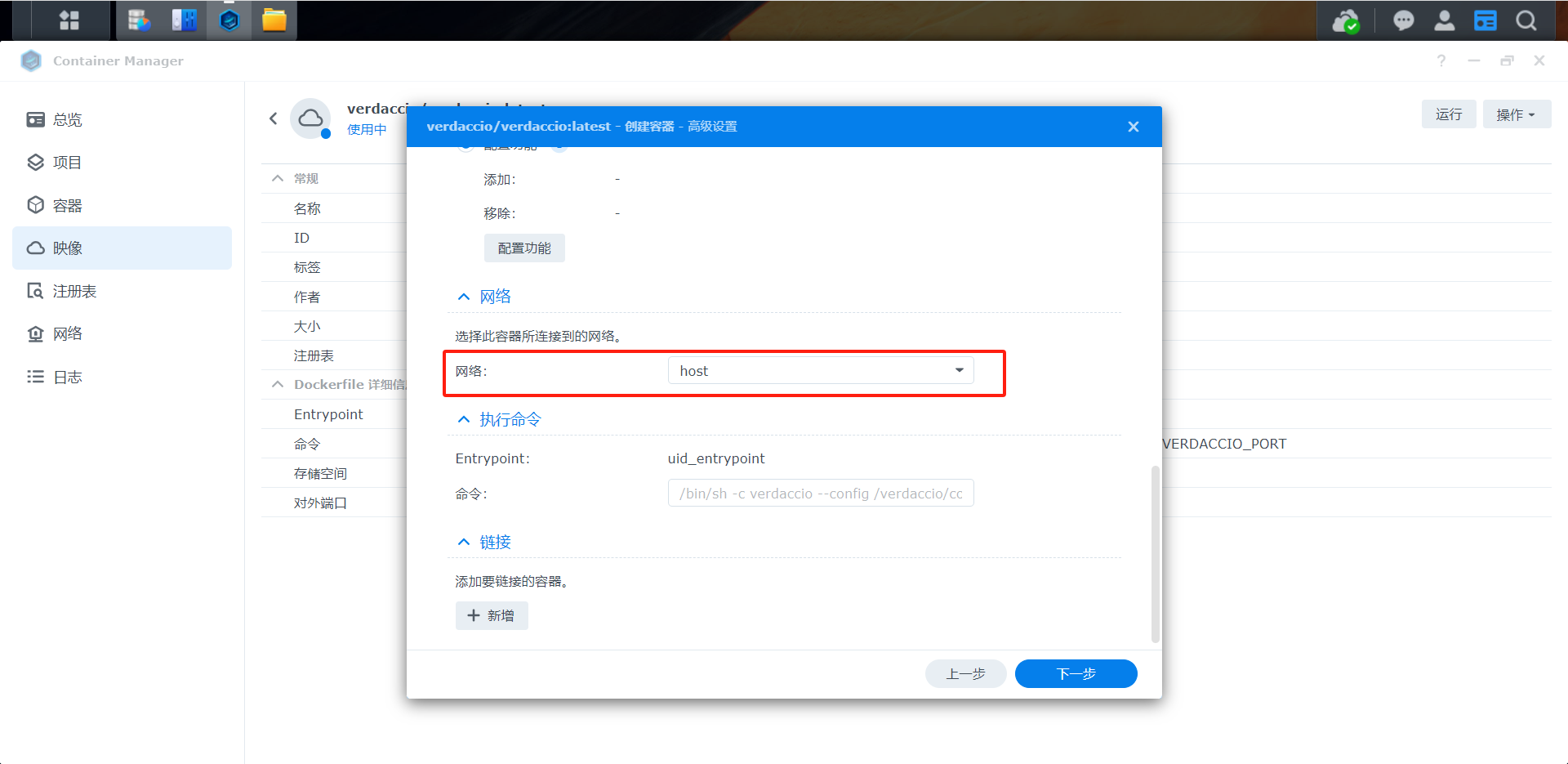
群晖NAS:docker(Container Manager)、npm安装Verdaccio并常见命令集合
群晖NAS:docker(Container Manager)、npm安装Verdaccio并常见命令集合 自建 npm 资源库,使用Verdaccio。如果觉得麻烦,直接可以在外网注册 https://www.npmjs.com/ 网站。大同小异,自己搭建搭建方便局域网…...

老师旁听公开课到底听什么
经常参加公开课是老师提升自己教学水平的一种方式。那么,在旁听公开课时,老师应该听什么呢? 听课堂氛围 一堂好的公开课,应该能够让学生积极参与,课堂气氛活跃,而不是老师一个人唱独角戏。如果老师能够引导…...

一文让你深入了解JavaSE的知识点
꒰˃͈꒵˂͈꒱ write in front ꒰˃͈꒵˂͈꒱ ʕ̯•͡˔•̯᷅ʔ大家好,我是xiaoxie.希望你看完之后,有不足之处请多多谅解,让我们一起共同进步૮₍❀ᴗ͈ . ᴗ͈ აxiaoxieʕ̯•͡˔•̯᷅ʔ—CSDN博客 本文由xiaoxieʕ̯•͡˔•̯᷅ʔ 原创 CSDN …...

人体是否有清除hpv病毒能力?北京劲松HPV诊疗中心提出观点
HPV,全称人乳头瘤病毒,是一种常见的性传播疾病,其症状包括尖锐湿疣、皮肤疣等。那么,人体是否有清除HPV病毒的能力呢?答案是肯定的,人体确实具有清除HPV病毒的能力。 首先,我们要了解HPV病毒是如何感染…...

Linux下~目录和home目录的区别
在 Linux 中,~(波浪号)路径和 home 路径都与用户的主目录(home directory)相关。 ~(波浪号)路径:表示当前登录用户的主目录。例如,如果你当前是以用户user1的身份登陆&am…...
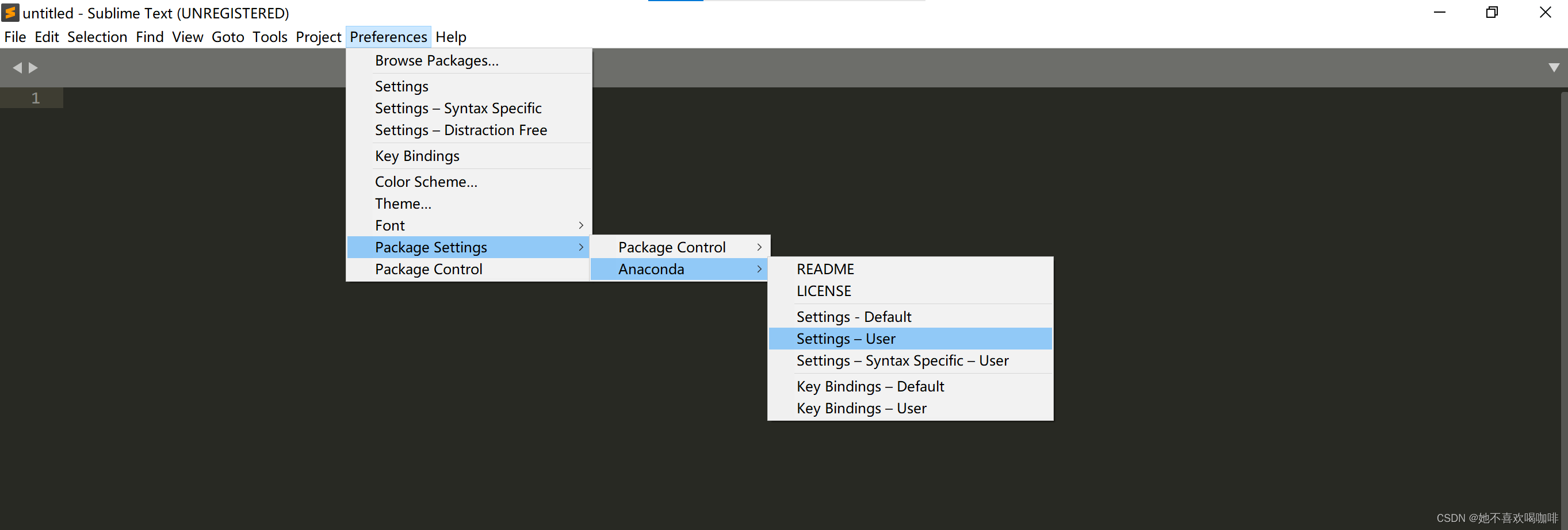
(二) Windows 下 Sublime Text 3 安装离线插件 Anaconda
1 下载 Sublime Text 3 免安装版 Download - Sublime Text 2 下载 Package Control,放到 Sublime Text Build 3211\Data\Installed Packages 目录下。 Installation - Package Control 3 页面搜索 anaconda anaconda - Search - Package Control Anaconda - Pac…...

如何实现大数据渲染
在前端实现大数据渲染时,常见的优化方式是使用虚拟滚动(Virtual Scrolling)或无限滚动(Infinite Scrolling)技术。这些技术可以帮助降低内存消耗和提高渲染性能,以下是一些常用的实现方法: 虚拟…...

【差旅游记】走进新疆哈密博物馆
哈喽,大家好,我是雷工! 前些天在新疆哈密时,有天下午有点时间,看离住的宾馆不远就是哈密博物馆,便去逛了逛博物馆,由于接下来的一段时间没顾上记录,趁今天有些时间简单记录下那短暂的…...
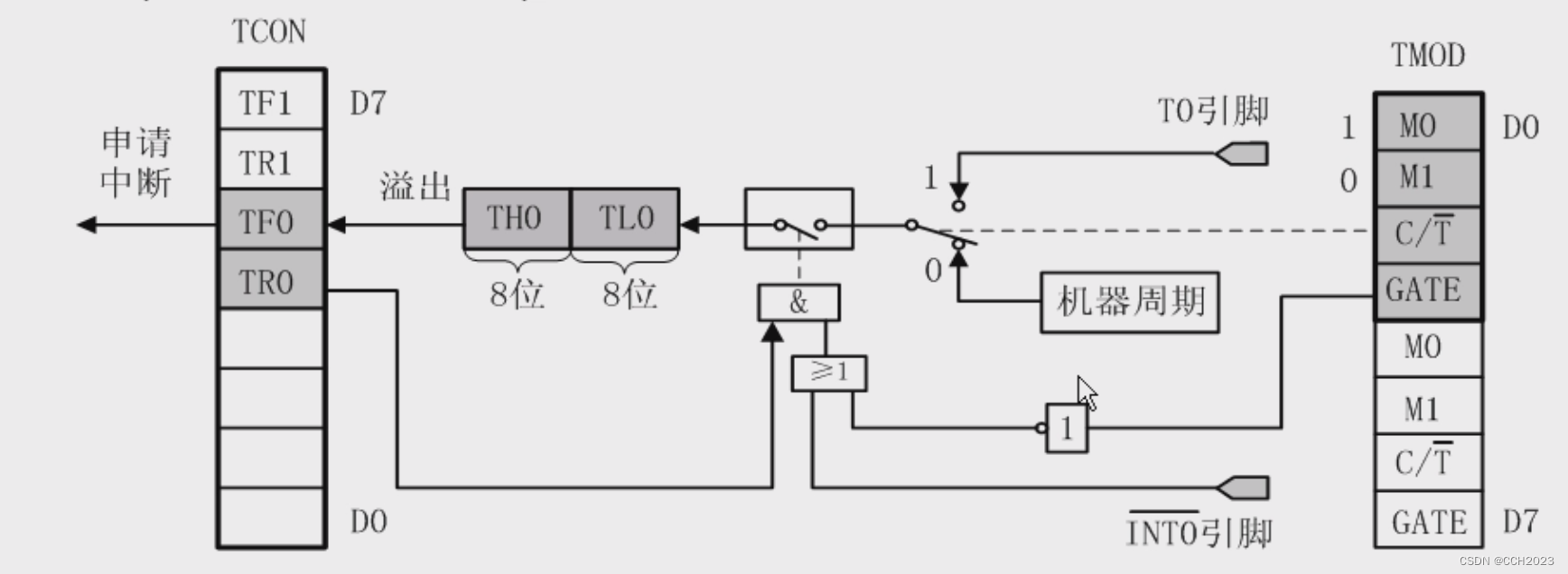
单片机学习6——定时器/计数功能的概念
在8051单片机中有两个定时器/计数器,分别是定时器/计数器0和定时器/计数器1。 T/C0: 定时器/计数器0 T/C1: 定时器/计数器1 T0: 定时器0 T1: 定时器1 C0: 计数器0 C1: 计数器1 如果是对内部振荡源12分频的脉冲信号进行计数,对每个机器周期计数&am…...
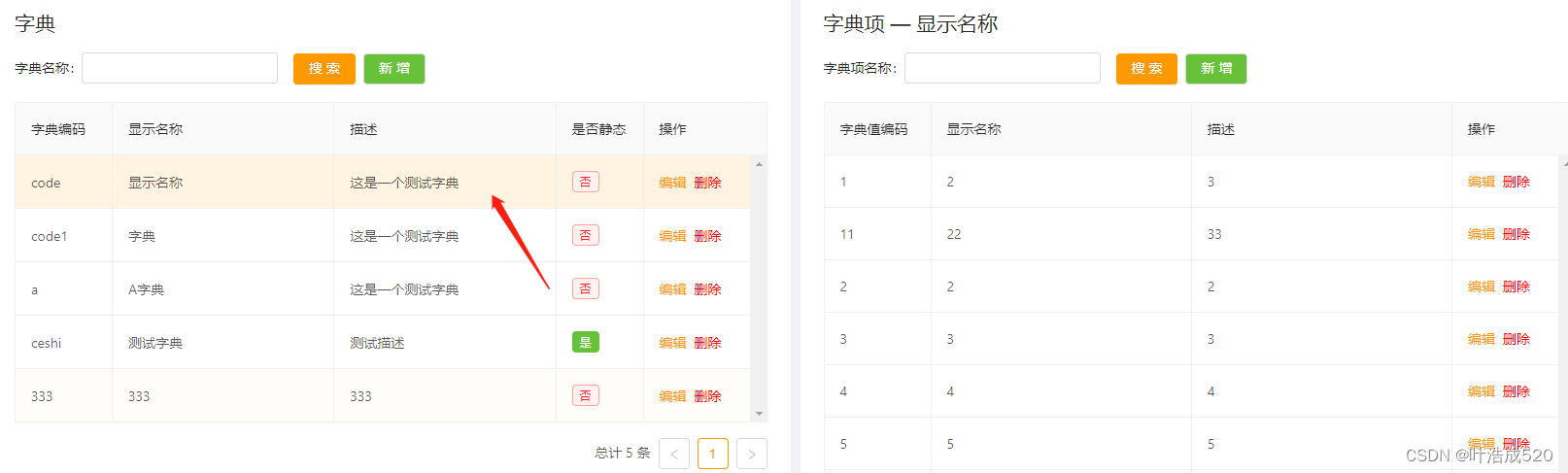
a-table:表格组件常用功能记录——基础积累2
antdvue是我目前项目的主流,在工作过程中,经常用到table组件。下面就记录一下工作中经常用到的部分知识点。 a-table:表格组件常用功能记录——基础积累2 效果图1.table 点击行触发点击事件1.1 实现单选 点击事件1.2 实现多选 点击事件1.3 实…...
leetCode 131.分割回文串 + 回溯算法 + 图解 + 笔记
131. 分割回文串 - 力扣(LeetCode) 给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是 回文串 。返回 s 所有可能的分割方案。回文串 是正着读和反着读都一样的字符串 示例 1: 输入:s "aa…...

浅谈对于Android CMakeLists文件的理解
文章目录 文件结构 文件结构 cmake_minimum_required(VERSION 3.10.2) //设置cmake版本set(CMAKE_LIBRARY_OUTPUT_DIRECTORY${CMAKE_CURRENT_LIST_DIR}/../jniLibs/${ANDROID_ABI}) //设置.so文件输出路径 project("add") //编译目录add_library( common //生成.so文…...
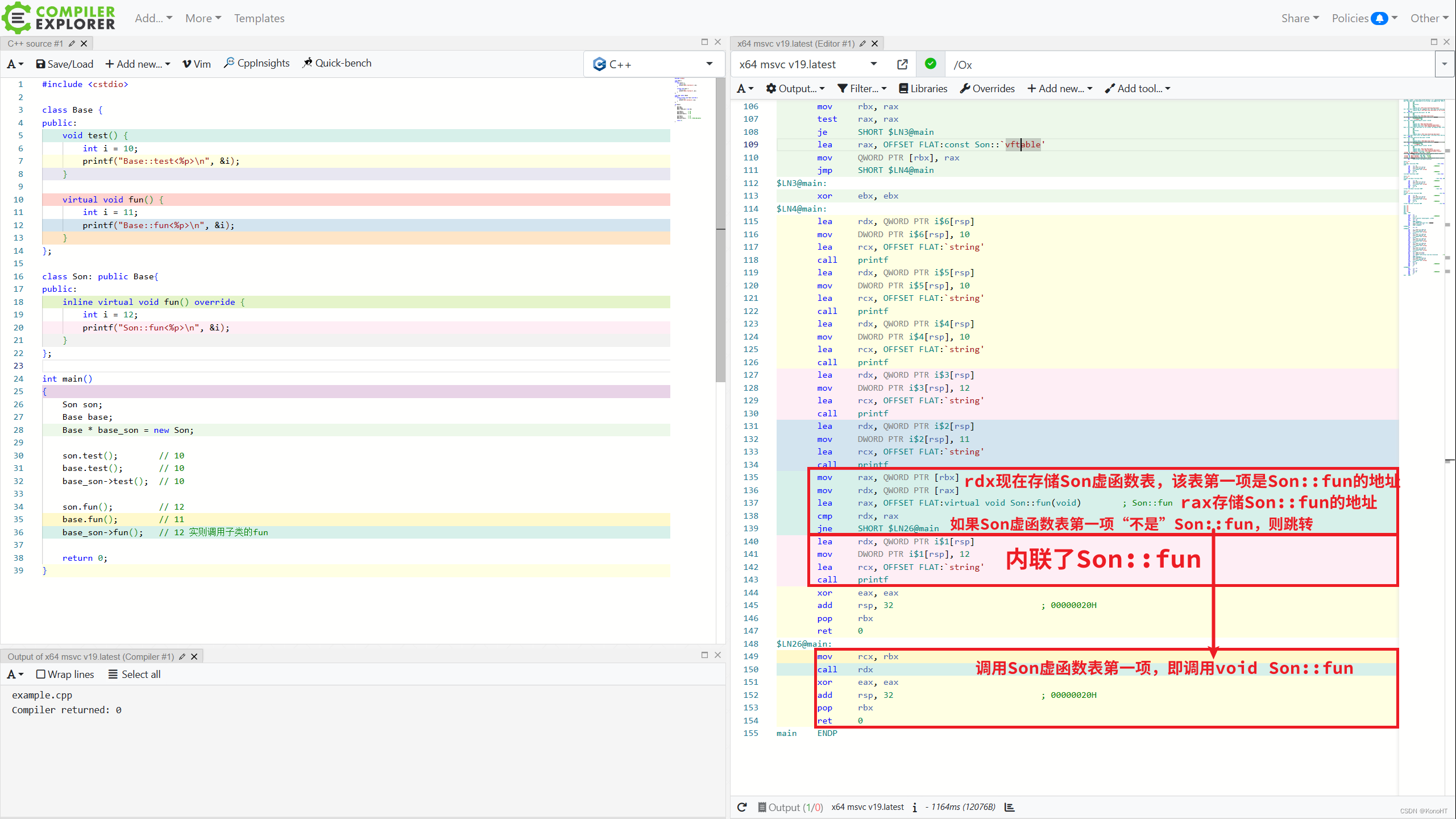
虚函数可不可以重载为内联 —— 在开启最大优化时gcc、clang和msvc的表现
下面是对该问题的一种常见回答: 首先,内联是程序员对编译器的一种建议,因此可以在在重载虚函数时在声明处加上inline关键字来修饰, 但是因为虚函数在运行时通过查找虚函数表调用的,而内联函数在编译时进行代码嵌入&…...

【开源】基于Vue+SpringBoot的智能教学资源库系统
项目编号: S 050 ,文末获取源码。 \color{red}{项目编号:S050,文末获取源码。} 项目编号:S050,文末获取源码。 目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 数据中心模块2.2 课程档案模块2.3 课…...

Sass基础知识之【变量】
文章目录 前言变量声明变量引用变量名用中划线还是下划线分隔后言 前言 hello world欢迎来到前端的新世界 😜当前文章系列专栏:Sass和Less 🐱👓博主在前端领域还有很多知识和技术需要掌握,正在不断努力填补技术短板。…...

云原生系列Go语言篇-泛型Part 1
“Don’t Repeat Yourself”是常见的软件工程建议。与其重新创建一个数据结构或函数,不如重用它,因为对重复的代码保持更改同步非常困难。在像 Go 这样的强类型语言中,每个函数参数及每个结构体字段的类型必须在编译时确定。这种严格性使编译…...

力扣1089题 复写零 双指针解法
2. 复写零 给你一个长度固定的整数数组 arr ,请你将该数组中出现的每个零都复写一遍,并将其余的元素向右平移。 注意:请不要在超过该数组长度的位置写入元素。请对输入的数组 就地 进行上述修改,不要从函数返回任何东西。 示例 1&…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...
