当前位置： 首页 > news >正文

TTS声音合成：paddlespeech、sherpa-onnx、coqui-ai

news 2026/2/10 12:13:44

1、百度TTS文本合成语音

参考：
https://aistudio.baidu.com/aistudio/projectdetail/5237474
https://www.jianshu.com/p/a7522ca6dec4
https://github.com/PaddlePaddle/PaddleSpeech/blob/develop/demos/text_to_speech/README_cn.md

1）过程中需要下载的TTS 声学相关模型（网络不好的话下面链接可以离线下载）：

PaddleSpeech支持的声学模型：['speedyspeech_csmsc-zh', 'fastspeech2_csmsc-zh', 'fastspeech2_canton-canton', 'fastspeech2_ljspeech-en', 'fastspeech2_aishell3-zh', 'fastspeech2_vctk-en', 'fastspeech2_cnndecoder_csmsc-zh', 'fastspeech2_mix-mix', 'fastspeech2_male-zh', 'fastspeech2_male-en', 'fastspeech2_male-mix', 'tacotron2_csmsc-zh', 'tacotron2_ljspeech-en', 'pwgan_csmsc-zh', 'pwgan_ljspeech-en', 'pwgan_aishell3-zh', 'pwgan_vctk-en', 'pwgan_male-zh', 'mb_melgan_csmsc-zh', 'style_melga

相关文章：

TTS声音合成：paddlespeech、sherpa-onnx、coqui-ai

1、百度TTS文本合成语音 参考： https://aistudio.baidu.com/aistudio/projectdetail/5237474 https://www.jianshu.com/p/a7522ca6dec4 https://github.com/PaddlePaddle/PaddleSpeech/blob/develop/demos/text_to_speech/README_cn.md 1）过程中需要下载的TTS 声学相关模型…...

编程日记 2023/12/1 0:30:07

Android frameworks 开发总结之十一

1.查看android关机前的log 有时候我们在没有连接电脑的情况下,会在测试的时候突然机器关机. 这个时候如果查看 log信息就看不到了。测试前可以执行下面的命令，之后再进行测试. $ adb shell $ nohup logcat > /sdcard/xxx.log 2.android日期时间同步 关于…...

编程日记 2023/12/1 0:28:05

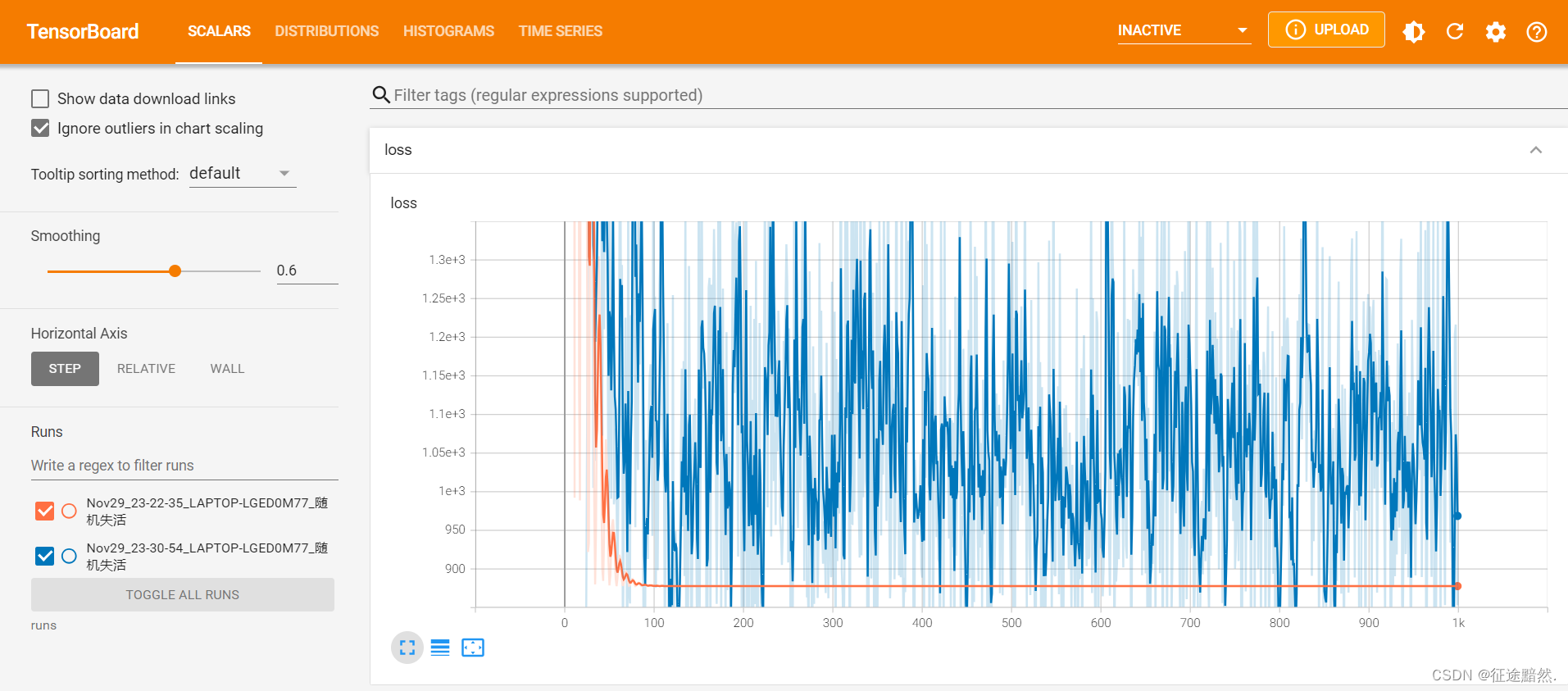
抑制过拟合——Dropout原理

抑制过拟合——Dropout原理 Dropout的工作原理 实验观察 在机器学习领域，尤其是当我们处理复杂的模型和有限的训练样本时，一个常见的问题是过拟合。简而言之，过拟合发生在模型对训练数据学得太好，以至于它捕捉到了数据中的噪声和…...

编程日记 2023/12/1 0:26:04

开发板启动进入系统以后再挂载 NFS 文件系统, 这里的NFS文件系统是根据正点原子教程制作的ubuntu_rootfs

如果是想开发板启动进入系统以后再挂载 NFS 文件系统，开发板启动进入文件系统，开发板和 ubuntu 能互相 ping 通，在开发板文件系统下新建一个目录 you，然后执行如下指令进行挂载： mkdir mi mount -t nfs -o nolock,nfsv…...

编程日记 2023/12/1 0:24:02

Ubuntu系统执行“docker ps“出现“permission denied“

当我们安装好Ubuntu时，使用鱼香ros一键安装指令 wget http://fishros.com/install -O fishros && . fishros 一键安装Docker后，执行"docker ps"出现"permission denied" seelina:~$ docker ps permission denied while …...

编程日记 2023/12/1 0:22:00

Python与设计模式--桥梁模式

23种计模式之 前言 （5）单例模式、工厂模式、简单工厂模式、抽象工厂模式、建造者模式、原型模式、(7)代理模式、装饰器模式、适配器模式、门面模式、组合模式、享元模式、桥梁模式、（11）策略模式、责任链模式、命令模式、中介者模…...

编程日记 2023/12/1 0:20:59

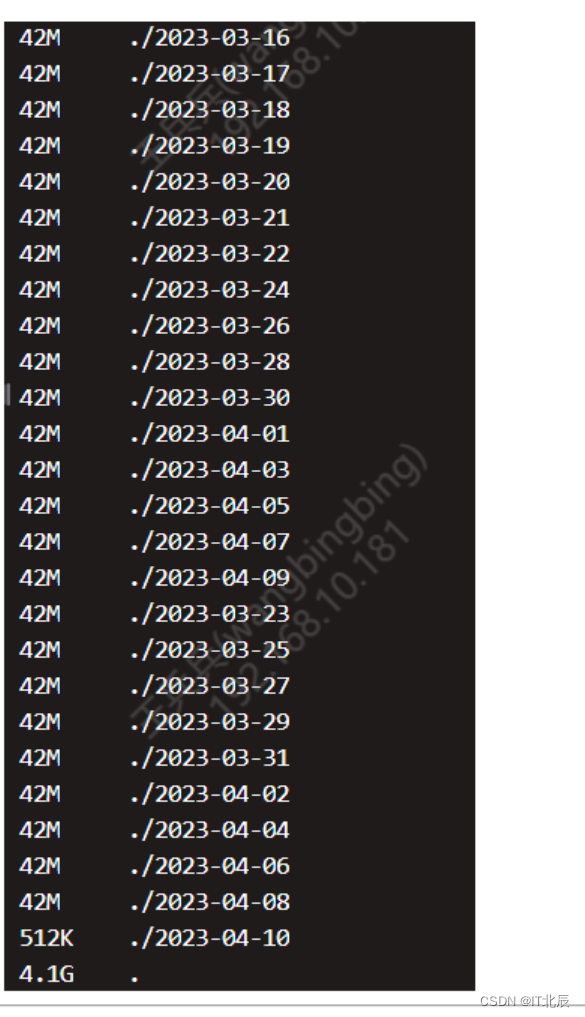
Linux下查看目录大小

查看目录大小 Linux下查看当前目录大小，可用一下命令： du -h --max-depth1它会从下到大的显示文件的大小。...

编程日记 2023/12/1 0:18:57

鸿蒙原生应用/元服务开发-AGC分发如何下载管理Profile

一、收到通知 尊敬的开发者： 您好，为支撑鸿蒙生态发展，HUAWEI AppGallery Connect已于X月XX日完成存量HarmonyOS应用/元服务的Profile文件更新，更新后Profile文件中已扩展App ID信息；后续上架流程会检测API9以上Harm…...

编程日记 2023/12/1 0:17:55

解决warning: #188-D: enumerated type mixed with another type问题

出现问题处如下， 指示在代码的某处将枚举类型与另一种类型混合使用，这种警告通常在将枚举类型与其他类型进行操作或赋值时出现 enum Mode {MODE_IDLE,MODE_1,MODE_2,MODE_3,MODE_4, }; enum Mode currentMode MODE_IDLE;currentMode (currentMode 1)…...

编程日记 2023/12/1 0:16:54

docker的知识点，以及使用

Docker 是一个开源的应用容器引擎，可以让开发者将应用程序及其依赖项打包至一个可移植的容器中，从而实现快速部署、可扩展和依赖项隔离等特性。下面是 Docker 的一些知识点以及使用方法： Docker 的组成部分包括 Docker 引擎、Docker 镜像、Do…...

编程日记 2023/12/1 0:15:52

WTM（基于Blazor）问题处理记录

问题描述一 有个需求，需要访问内网网络共享文件夹中的文件，有域控限制。 一开始直接在本地映射一个网络驱动器，然后像本地磁盘一样访问共享文件夹里的文件，比如：Y:\ 。 然后直接在程序中访问共享文件夹中的文件，如下代码： DirectoryInfo directoryInfo = new Direct…...

编程日记 2023/12/1 0:14:51

ubuntu 安装 towhee

安装Towhee pip3 install towhee如果你想在 towhee 中安装模型 pip3 install towhee.models打开python终端 python3引入towhee 数据转换是 Towhee 的核心；管道只是在有向无环图中连接在一起的一系列转换。所有预构建的 Towhee 管道都有代表当前任务的名称。 fr…...

编程日记 2023/12/1 0:12:50

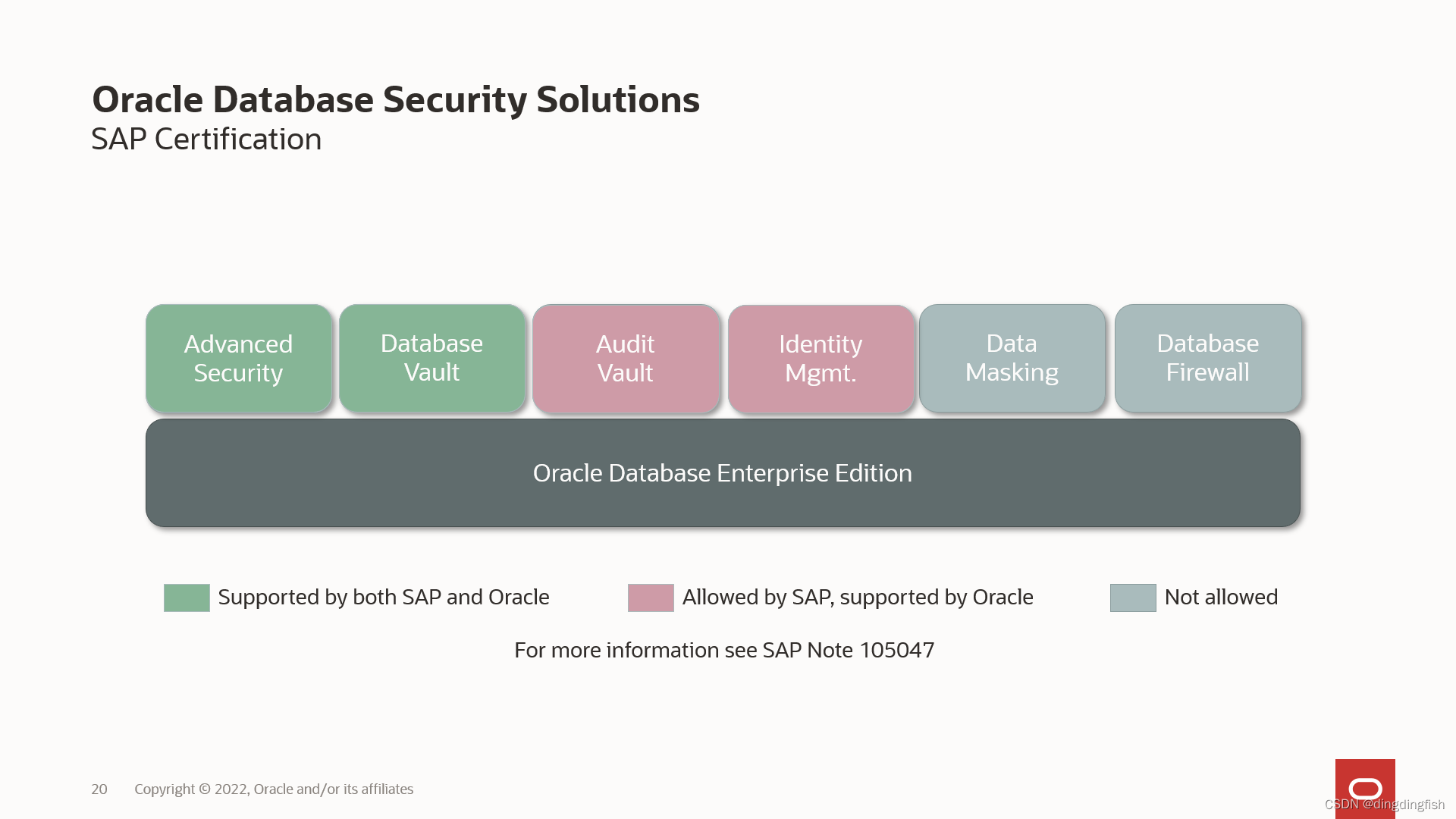
ERP软件对Oracle安全产品的支持

这里的ERP软件仅指SAP ECC和Oracle EBS。 先来看Oracle EBS： EBS的认证查询方式，和数据库认证是一样的。这个体验到时不错。 结果中和安全相关的有： Oracle Database VaultTransparent Data Encryption TDE被支持很容易理解，…...

编程日记 2023/12/1 0:10:48

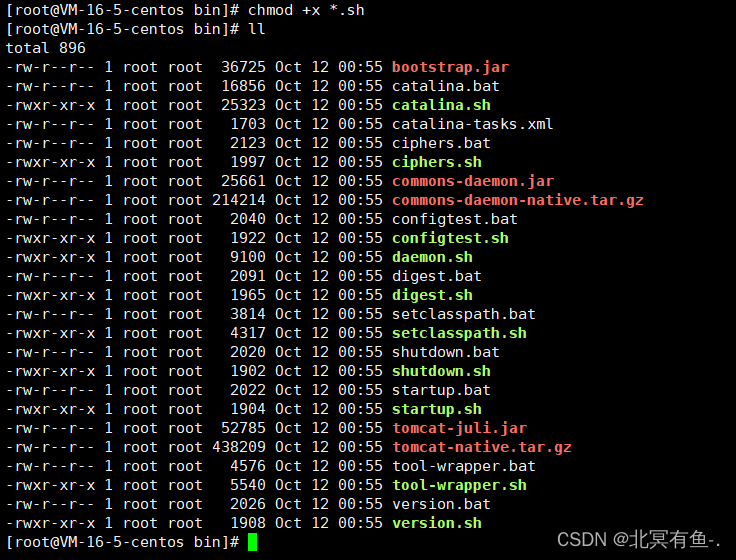
Linux 基础-常用的命令和搭建 Java 部署环境

文章目录 目录相关查看目录中的内容查看目录当前的完整路径切换目录 文件相关创建文件查看文件内容写文件vim 基础 创建删除创建目录 移动和复制移动(剪切粘贴)复制(复制粘贴) 搭建 Java 部署环境1. 安装 jdk2. 安装 tomcat1). 我们在自己电脑上下好 tomcat2). 从官网下载的 .z…...

编程日记 2023/12/1 0:09:47

c语言总结（解题方法）

项目前期处理： 1.首先需要确定项目的背景知识，即主要的难点知识，如指针，数组，结构体，以检索自己是否对项目所需的背景知识足够了解。 2.确定问题实现方法，即题目本身的实现方法，在c语…...

编程日记 2023/12/1 0:05:43

Webpack的ts的配置详细教程

文章目录 前言ts是什么？基础配置LoaderSource MapsClient types使用第三方类库导入其他资源 后言 前言 hello world欢迎来到前端的新世界 😜当前文章系列专栏：webpack 🐱‍👓博主在前端领域还有很多知识和技术需要掌握…...

编程日记 2023/12/1 0:04:41

传智杯第五届题解

B.莲子的机械动力学 分析&#xff1a;这题有个小坑&#xff0c;如果是00 0&#xff0c;结果记得要输出0。 得到的教训是&#xff0c;避免前导0出现时&#xff0c;要注意答案为0的情况。否则有可能会没有输出 #include<assert.h> #include<cstdio> #include<…...

编程日记 2023/12/1 0:02:39

Android 通过demo调试节点权限问题

Android 通过demo调试节点权限问题 近来收到客户反馈提到在应用层无法控制节点&#xff0c;于是写了一个简单的demo来验证节点的IO权限&#xff0c;具体调试步骤就是写一个按钮点击事件&#xff0c;当点击按钮时将需要验证的节点写为1&#xff08;节点默认为1则写为0&#xff…...

编程日记 2023/12/1 0:01:38

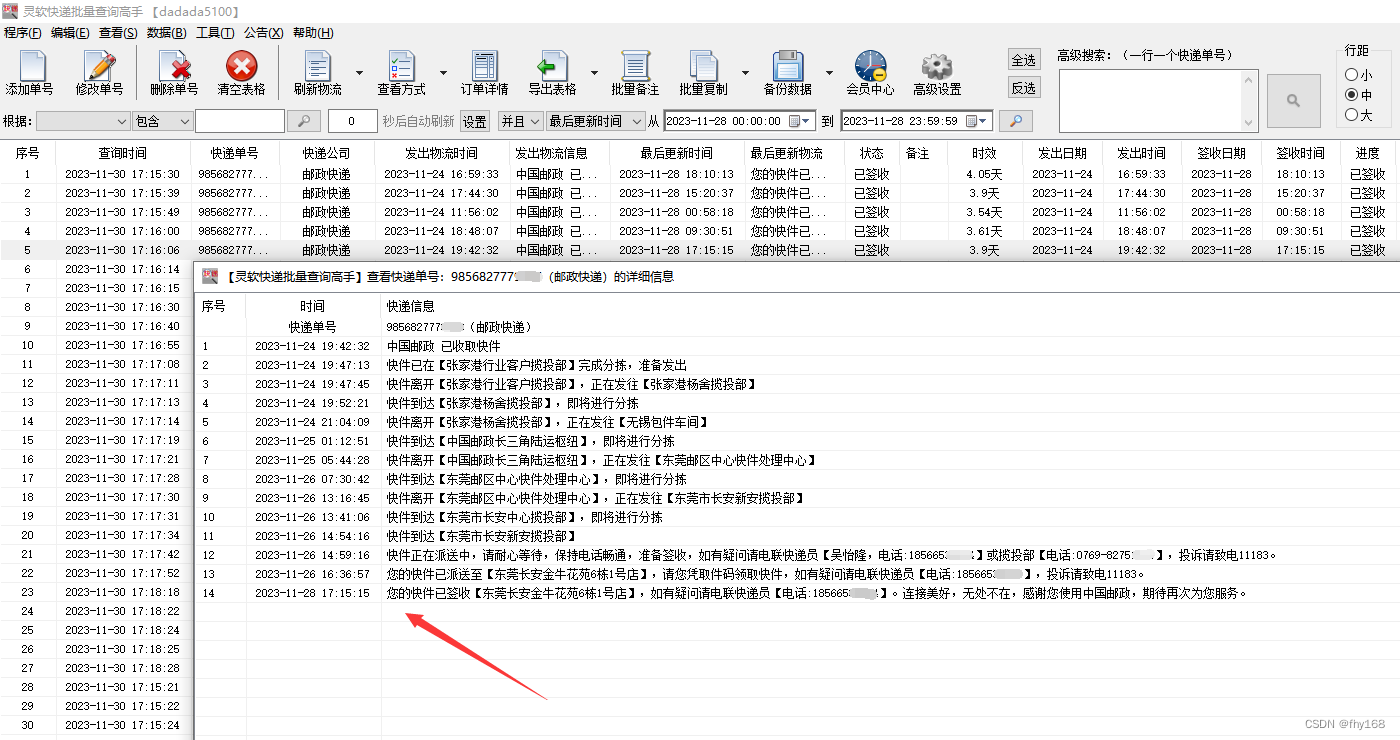
邮政快递物流查询，将指定某天签收的单号筛选出来

批量查询邮政快递单号的物流信息&#xff0c;将指定某天签收的单号筛选出来。 所需工具&#xff1a; 一个【快递批量查询高手】软件 邮政快递单号若干 操作步骤&#xff1a; 步骤1&#xff1a;运行【快递批量查询高手】软件&#xff0c;并登录 步骤2&#xff1a;点击主界面左…...

编程日记 2023/12/1 0:00:34

Java 8 lambda的一个编译bug

最近利用github action向Maven中央仓库发布企业微信SDK时会失败&#xff0c;从日志中发现是系统资源耗尽了&#xff0c;日志如下&#xff1a; [INFO] Changes detected - recompiling the module! :dependency [INFO] Compiling 35 source files with javac [debug target 8] …...

编程日记 2023/11/30 23:59:34

UDP(Echoserver)

网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法&#xff1a;netstat [选项] 功能&#xff1a;查看网络状态 常用选项&#xff1a; n 拒绝显示别名&#…...

编程新知 2026/1/24 7:56:15

定时器任务——若依源码分析

分析util包下面的工具类schedule utils&#xff1a; ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类&#xff0c;封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz&#xff0c;先构建任务的 JobD…...

编程新知 2026/1/26 14:24:46

Python Ovito统计金刚石结构数量

大家好，我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构，但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法，可以持续统计各步的金刚石结构，具体代码如下： from ovito…...

编程新知 2026/1/26 5:39:08

【JVM】Java虚拟机（二）——垃圾回收

目录 一、如何判断对象可以回收 &#xff08;一&#xff09;引用计数法 &#xff08;二&#xff09;可达性分析算法 二、垃圾回收算法 &#xff08;一&#xff09;标记清除 &#xff08;二&#xff09;标记整理 &#xff08;三&#xff09;复制 &#xff08;四&#xff…...

编程新知 2026/1/31 9:49:23

多模态图像修复系统：基于深度学习的图片修复实现

多模态图像修复系统：基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型（Stable Diffusion Inpainting）实现图像修复功能，结合文本描述和图片输入，对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

编程新知 2025/9/9 21:28:16

全面解析数据库：从基础概念到前沿应用​

在数字化时代&#xff0c;数据已成为企业和社会发展的核心资产&#xff0c;而数据库作为存储、管理和处理数据的关键工具&#xff0c;在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理&#xff0c;到社交网络的用户数据存储&#xff0c;再到金融行业的交易记录处理&a…...

编程新知 2025/9/19 11:48:17

CVE-2023-25194源码分析与漏洞复现(Kafka JNDI注入)

漏洞概述 漏洞名称&#xff1a;Apache Kafka Connect JNDI注入导致的远程代码执行漏洞 CVE编号&#xff1a;CVE-2023-25194 CVSS评分&#xff1a;8.8 影响版本&#xff1a;Apache Kafka 2.3.0 - 3.3.2 修复版本&#xff1a;≥ 3.4.0 漏洞类型&#xff1a;反序列化导致的远程代…...

编程新知 2026/2/8 21:48:54

简约商务通用宣传年终总结12套PPT模版分享

IOS风格企业宣传PPT模版&#xff0c;年终工作总结PPT模版&#xff0c;简约精致扁平化商务通用动画PPT模版&#xff0c;素雅商务PPT模版 简约商务通用宣传年终总结12套PPT模版分享:商务通用年终总结类PPT模版https://pan.quark.cn/s/ece1e252d7df...

编程新知 2026/2/8 13:56:36

基于谷歌ADK的 智能产品推荐系统(2): 模块功能详解

在我的上一篇博客&#xff1a;基于谷歌ADK的 智能产品推荐系统(1): 功能简介-CSDN博客 中我们介绍了个性化购物 Agent 项目&#xff0c;该项目展示了一个强大的框架&#xff0c;旨在模拟和实现在线购物环境中的智能导购。它不仅仅是一个简单的聊天机器人&#xff0c;更是一个集…...

编程新知 2026/1/28 2:54:17

SFTrack：面向警务无人机的自适应多目标跟踪算法——突破小尺度高速运动目标的追踪瓶颈

【导读】 本文针对无人机&#xff08;UAV&#xff09;视频中目标尺寸小、运动快导致的多目标跟踪难题&#xff0c;提出一种更简单高效的方法。核心创新在于从低置信度检测启动跟踪&#xff08;贴合无人机场景特性&#xff09;&#xff0c;并改进传统外观匹配算法以关联此类检测…...

编程新知 2026/1/28 8:46:16