计算理论 复杂度预备知识
文章目录
- 计算理论 复杂度预备知识
- 符号
- 递归表达式求解通项公式
- 主方法
- Akra-Bazzi 定理
计算理论 复杂度预备知识
符号
f(n)=o(g(n))f(n)=o(g(n))f(n)=o(g(n)) :∃c\exists c∃c ,当 nnn 足够大时, f(n)<cg(n)f(n)\lt cg(n)f(n)<cg(n) ;∑n→∞f(n)g(n)=0\sum\limits_{n\to\infty} \frac{f(n)}{g(n)}=0n→∞∑g(n)f(n)=0 ;
f(n)=O(g(n))f(n)=O(g(n))f(n)=O(g(n)) :∃c\exists c∃c ,当 nnn 足够大时, f(n)≤cg(n)f(n)\le cg(n)f(n)≤cg(n) ;
f(n)=θ(g(n))f(n)=\theta(g(n))f(n)=θ(g(n)) :∃c1,c2\exists c_{1}, c_{2}∃c1,c2 ,当 nnn 足够大时, c1g(n)<f(n)<c2g(n)c_{1}g(n)\lt f(n) \lt c_{2}g(n)c1g(n)<f(n)<c2g(n) ;
f(n)=ω(g(n))f(n)=\omega(g(n))f(n)=ω(g(n)) :∃c\exists c∃c ,当 nnn 足够大时, f(n)>cg(n)f(n)\gt cg(n)f(n)>cg(n) ;
f(n)=Ω(g(n))f(n)=\Omega(g(n))f(n)=Ω(g(n)) :∃c\exists c∃c ,当 nnn 足够大时, f(n)≥cg(n)f(n)\ge cg(n)f(n)≥cg(n) ;
递归表达式求解通项公式
① T(n)=4T(n2)+nT(n)=4T\left( \frac{n}{2} \right)+nT(n)=4T(2n)+n :就直接展开,找到规律
T(n)=4T(n2)+n=4(4(T(n22)+n2)+n=4T(n22)+2n+n=4kT(n2k)+n(20+21+⋯+2k−1)\begin{array}{l} \quad T(n) \\ =4T(\frac{n}{2})+n \\ =4(4(T(\frac{n}{2^{2}})+\frac{n}{2})+n \\ =4T(\frac{n}{2^{2}})+2n+n \\ =4^{k}T(\frac{n}{2^{k}})+n(2^0+2^1+\dots+2^{k-1}) \end{array} T(n)=4T(2n)+n=4(4(T(22n)+2n)+n=4T(22n)+2n+n=4kT(2kn)+n(20+21+⋯+2k−1)
假设 nnn 是 2 的幂,则最后 kkk 应该等于 log2(n)\log_{2}(n)log2(n) ,故:
T(n)=T(1)n2+n∑i=1log2(n)2i−1=T(1)n2+n(n−1)=O(n2)T(n)=T(1)n^{2}+n\sum\limits_{i=1}^{\log_{2}(n)}2^{i-1}=T(1)n^{2}+n(n-1)=O(n^{2}) T(n)=T(1)n2+ni=1∑log2(n)2i−1=T(1)n2+n(n−1)=O(n2)
② T(n)=2T(n2)+n=nT(1)+nlog2(n)=O(nlogn)T(n)=2T(\frac{n}{2})+n=nT(1)+n\log_{2}(n)=O(n\log{n})T(n)=2T(2n)+n=nT(1)+nlog2(n)=O(nlogn)
③ T(n)=4T(n2)+n2=n2T(1)+n2log2n=O(n2logn)T(n)=4T(\frac{n}{2})+n^{2}=n^{2}T(1)+n^{2}\log_{2}{n}=O(n^{2}\log{n})T(n)=4T(2n)+n2=n2T(1)+n2log2n=O(n2logn)
④ T(n)=2T(n2)+n2=nT(1)+2n2=O(n2)T(n)=2T(\frac{n}{2})+n^2=nT(1)+2n^{2}=O(n^{2})T(n)=2T(2n)+n2=nT(1)+2n2=O(n2)
⑤ T(n)=4T(n2)+n2lognT(n)=4T(\frac{n}{2})+\frac{n^{2}}{\log{n}}T(n)=4T(2n)+lognn2
T(n)=4T(n2)+n2logn=n2T(1)+n2logn+n2logn−1+⋯+n2log1=θ(n2loglogn)\begin{array}{l} \quad T(n) \\ =4T(\frac{n}{2})+\frac{n^{2}}{\log{n}} \\ =n^{2}T(1)+\frac{n^{2}}{\log{n}}+\frac{n^{2}}{\log{n-1}}+\dots+\frac{n^{2}}{\log{1}} \\ =\theta(n^{2}\log{\log{n}}) \end{array} T(n)=4T(2n)+lognn2=n2T(1)+lognn2+logn−1n2+⋯+log1n2=θ(n2loglogn)
因为这个级数可以看成积分:
1x+1x−1+1x−2+⋯=∫1xdx=lnx\frac{1}{x}+\frac{1}{x-1}+\frac{1}{x-2}+\dots=\int_{1}^x \, dx=\ln{x} x1+x−11+x−21+⋯=∫1xdx=lnx
主方法
Th:设 a≥1a\geq 1a≥1 ,b≥1b\geq 1b≥1 ,f(n)f(n)f(n) 为一定义在非负整数上的函数,T(n)=aT(nb)+f(n)T(n)=aT(\frac{n}{b})+f(n)T(n)=aT(bn)+f(n) (当 nb\frac{n}{b}bn 不为整数时代表 ⌈nb⌉\lceil \frac{n}{b} \rceil⌈bn⌉ 或 ⌊nb⌋\lfloor \frac{n}{b} \rfloor⌊bn⌋ ),则:
- 若 ∃ε>0\exists \varepsilon>0∃ε>0 ,使得 f(n)=O(nlogba−ε)f(n)=O(n^{\log_{b}{a}-\varepsilon})f(n)=O(nlogba−ε) ,则 T(n)=Θ(nlogba)T(n)=\Theta(n^{\log_{b}{a}})T(n)=Θ(nlogba)
- 若 ∃k≥0\exists k\geq 0∃k≥0 ,使得 f(n)=Θ(nlogbalgkn)f(n)=\Theta(n^{\log_{b}{a}\,lg^k{n}})f(n)=Θ(nlogbalgkn) ,则 T(n)=Θ(nlogbalgk+1n)T(n)=\Theta(n^{\log_{b}{a}}\,lg^{k+1}{n})T(n)=Θ(nlogbalgk+1n)
- 若 ∃ε>0\exists \varepsilon>0∃ε>0 ,使得 f(n)=Ω(nlogba+ε)f(n)=\Omega(n^{\log_{b}{a}+\varepsilon})f(n)=Ω(nlogba+ε) ,且存在 0<c<10<c<10<c<1 以及正整数 N0N_{0}N0 ,使得当 n>N0n>N_{0}n>N0 时,有 af(nb)≤cf(n)af(\frac{n}{b})\leq cf(n)af(bn)≤cf(n) ,则 T(n)=Θ(f(n))T(n)=\Theta(f(n))T(n)=Θ(f(n))
证明:首先展开,得到:
T(n)=aT(nb)+f(n)=a(aT(nb2)+f(nb))+f(n)a2T(nb2)+af(nb)+f(n)=…=alogbnT(1)+∑i=0logbn−1aif(nbi)\begin{array}{l} \quad T(n) \\ =aT(\frac{n}{b})+f(n) \\ =a(aT(\frac{n}{b^2})+f(\frac{n}{b}))+f(n) \\ a^2T(\frac{n}{b^{2}})+af(\frac{n}{b})+f(n) \\ =\dots \\ =a^{\log_{b}{n}}T(1)+\sum\limits_{i=0}^{\log_{b}{n}-1}a^if(\frac{n}{b^i}) \end{array} T(n)=aT(bn)+f(n)=a(aT(b2n)+f(bn))+f(n)a2T(b2n)+af(bn)+f(n)=…=alogbnT(1)+i=0∑logbn−1aif(bin)
其中 alogbn=blogbalogbn=nlogbaa^{\log_{b}{n}}=b^{\log_{b}a\log_{b}n}=n^{\log_{b}a}alogbn=blogbalogbn=nlogba ;如果把 f(n)f(n)f(n) 看成多项式的话,只需要比较 f(n)f(n)f(n) 的次数与 logba\log_{b}alogba 的相对大小;
① 若 ∃ε>0\exists \varepsilon>0∃ε>0 ,使得 f(n)=O(nlogba−ε)f(n)=O(n^{\log_{b}{a}-\varepsilon})f(n)=O(nlogba−ε) ,则 T(n)=Θ(nlogba)T(n)=\Theta(n^{\log_{b}{a}})T(n)=Θ(nlogba)
∑i=0logbn−1aif(nbi)=∑ai(nb)logba−ε=∑nlogba−ε−biεai=nlogba−ε∑biε=nlogba−ε1−nε1−bε=O(nlogba)\begin{array}{l} \quad\sum\limits_{i=0}^{\log_{b}{n}-1}a^if\left( \frac{n}{b^i} \right) \\ =\sum\limits a^i\left( \frac{n}{b} \right)^{\log_{b}a-\varepsilon} \\ =\sum\limits \frac{n^{\log_{b}a-\varepsilon}-b^{i\varepsilon}}{a^i} \\ =n^{\log_{b}a-\varepsilon}\sum\limits b^{i\varepsilon} \\ =n^{\log_{b}a-\varepsilon} \frac{1-n^{\varepsilon}}{1-b^{\varepsilon}} \\ =O(n^{\log_{b}a}) \end{array} i=0∑logbn−1aif(bin)=∑ai(bn)logba−ε=∑ainlogba−ε−biε=nlogba−ε∑biε=nlogba−ε1−bε1−nε=O(nlogba)
② 若 ∃k≥0\exists k\geq 0∃k≥0 ,使得 f(n)=Θ(nlogbalgkn)f(n)=\Theta(n^{\log_{b}{a}\,lg^k{n}})f(n)=Θ(nlogbalgkn) ,则 T(n)=Θ(nlogbalgk+1n)T(n)=\Theta(n^{\log_{b}{a}}\,lg^{k+1}{n})T(n)=Θ(nlogbalgk+1n)
我们就假设 f(n)=nlogbalgknf(n)=n^{\log_{b}a}\lg^k{n}f(n)=nlogbalgkn ,则:
∑i=0logbn−1aif(nbi)=∑ai(nbi)logbalgk(nbi)=∑ainlogbaai(lgn−ilgb)k\begin{array}{l} \quad\sum\limits_{i=0}^{\log_{b}{n}-1}a^if\left( \frac{n}{b^i} \right) \\ =\sum\limits a^{i}(\frac{n}{b^{i}})^{\log_{b}{a}}\lg^k{(\frac{n}{b^i})} \\ =\sum\limits a^{i}\frac{n^{\log_{b}a}}{a^{i}}(\lg{n}-i\lg{b})^k \end{array} i=0∑logbn−1aif(bin)=∑ai(bin)logbalgk(bin)=∑aiainlogba(lgn−ilgb)k
这个 (lgn−ilgb)k(\lg{n}-i\lg{b})^k(lgn−ilgb)k 二项展开的话会发现,次数肯定是 lgkn\lg^k{n}lgkn 决定的,则:
≈∑nlogbalgkn=logbn⋅nlogbalgkn=nlogbalgk+1n\begin{array}{l} \approx \sum\limits n^{\\log_{b}a}\lg^k{n} \\ =\log_{b}{n} \cdot n^{\\log_{b}a}\lg^k{n} \\ =n^{\log_{b}{a}}\,lg^{k+1}{n} \end{array} ≈∑nlogbalgkn=logbn⋅nlogbalgkn=nlogbalgk+1n
③ 若 ∃ε>0\exists \varepsilon>0∃ε>0 ,使得 f(n)=Ω(nlogba+ε)f(n)=\Omega(n^{\log_{b}{a}+\varepsilon})f(n)=Ω(nlogba+ε) ,且存在 0<c<10<c<10<c<1 以及正整数 N0N_{0}N0 ,使得当 n>N0n>N_{0}n>N0 时,有 af(nb≤cf(n))af(\frac{n}{b}\leq cf(n))af(bn≤cf(n)) ,则 T(n)=Θ(f(n))T(n)=\Theta(f(n))T(n)=Θ(f(n))
当满足条件时,有 cf(n)≥af(nb)cf(n)\geq af(\frac{n}{b})cf(n)≥af(bn) ,得到:
f(n)≥acf(nb)≥a2c2f(nb2)≥⋯≥aicif(nbi)f(n)\geq \frac{a}{c}f(\frac{n}{b}) \geq \frac{a^{2}}{c^{2}}f(\frac{n}{b^{2}})\geq\dots\geq\frac{a^{i}}{c^{i}}f(\frac{n}{b^{i}}) f(n)≥caf(bn)≥c2a2f(b2n)≥⋯≥ciaif(bin)
故 f(n)≥aicif(nbi)f(n)\geq\frac{a^{i}}{c^{i}}f(\frac{n}{b^{i}})f(n)≥ciaif(bin) ;需要满足所有大于等于的条件,发现只需要最后一个大于等于满足即可,即 nbi>N0⟹i<logbn−logbN0+1\frac{n}{b^{i}}\gt N_{0}\implies i< \log_{b}n-\log_{b}{N_{0}}+1bin>N0⟹i<logbn−logbN0+1
∑i=0logbn−1aif(nbi)=∑i=0logbn−logbN0aif(nbi)+∑i=logbn−logbN0+1logbn−1aif(nbi)\begin{array}{l} \quad\sum\limits_{i=0}^{\log_{b}{n}-1}a^if\left( \frac{n}{b^i} \right) \\ =\sum\limits_{i=0}^{\log_{b}^n-\log_{b}^{N_{0}}} a^if\left( \frac{n}{b^i} \right)+\sum\limits_{i=\log_{b}^n-\log_{b}^{N_{0}}+1}^{\log_{b}n-1}a^if\left( \frac{n}{b^i} \right) \end{array} i=0∑logbn−1aif(bin)=i=0∑logbn−logbN0aif(bin)+i=logbn−logbN0+1∑logbn−1aif(bin)
左项是满足 i<logbn−logbN0+1i< \log_{b}n-\log_{b}{N_{0}}+1i<logbn−logbN0+1 的条件,有:
≤∑i=0logbn−logbN0cif(n)=O(f(n))\leq \sum\limits_{i=0}^{\log_{b}^n-\log_{b}^{N_{0}}}c^if(n)=O(f(n)) ≤i=0∑logbn−logbN0cif(n)=O(f(n))
右项是 O(1)O(1)O(1) ,展开也看不出来(直接把 f(n)f(n)f(n) 看作 O(nlogba+ε)O(n^{\log_{b}a+{\varepsilon}})O(nlogba+ε)):
=∑ai(nbi)logba+ε=∑ainlogba+εai⋅biε=nlogba+ε∑1biε=1−(1bε)logbN0−11−1bε⋅1bε(logbn−logbN0+1)⋅nlogba+ε\begin{array}{l} =\sum\limits a^i\left( \frac{n}{b^i} \right)^{\log_{b}a+\varepsilon} \\ =\sum\limits a^i\frac{n^{\log_{b}a+\varepsilon}}{a^i\cdot b^{i\varepsilon}} \\ =n^{\log_{b}a+\varepsilon}\sum\limits\frac{1}{b^{i\varepsilon}} \\ =\frac{1-(\frac{1}b^{\varepsilon})^{\log_{b}N_{0}-1}}{1-\frac{1}{b^{\varepsilon}}}\cdot \frac{1}{b^{\varepsilon(\log_{b}n-\log_{b}N_{0}+1)}} \cdot n^{\log_{b}a+\varepsilon} \end{array} =∑ai(bin)logba+ε=∑aiai⋅biεnlogba+ε=nlogba+ε∑biε1=1−bε11−(b1ε)logbN0−1⋅bε(logbn−logbN0+1)1⋅nlogba+ε
第一项是常数,后边两项乘起来看着像个常数
Akra-Bazzi 定理
Th:设 g(x)g(x)g(x) 为一非负函数,T(x)={Θ(1),1≤x≤X0∑i=1kaiT(xbi)+g(x),n>X0T(x)=\left\{\begin{array}{ll}\Theta(1) & ,1\leq x \leq X_{0} \\ \sum\limits_{i=1}^k a_{i}T(\frac{x}{b_{i}})+g(x)& ,n>X_{0} \end{array}\right.T(x)=⎩⎨⎧Θ(1)i=1∑kaiT(bix)+g(x),1≤x≤X0,n>X0 (其中 k≥1k\geq 1k≥1 ,ai>0a_{i}>0ai>0 ,bi>1b_{i}>1bi>1,X0X_{0}X0 满足对任意 1≤i≤k1\leq i\leq k1≤i≤k 有 X0>biX_{0}>b_{i}X0>bi 且 X0>bibi−1X_{0}>\frac{b_{i}}{b_{i}-1}X0>bi−1bi ),若 g(x)g(x)g(x) 满足多项式增长条件,ppp 为方程 ∑i=1kaibip=1\sum\limits_{i=1}^k\frac{a_{i}}{b_{i}^p}=1i=1∑kbipai=1 的实数解,则:
T(x)=Θ(xp(1+∫1xg(x)xp+1dx))T(x)=\Theta\left( x^p\left( 1+\int_{1}^x \frac{g(x)}{x^{p+1}}dx \right) \right) T(x)=Θ(xp(1+∫1xxp+1g(x)dx))
例:T(n)=2T(n4+3T(n6)+nlgn)T(n)=2T(\frac{n}{4}+3T(\frac{n}{6})+n\lg{n})T(n)=2T(4n+3T(6n)+nlgn)
解 24p+36p=1\frac{2}{4^p}+\frac{3}{6^p}=14p2+6p3=1 得 p=1p=1p=1
T(n)=Θ(n(1+∫1nxlgxx2dx))=Θ(n(1+12lg2n))=Θ(nlg2n)\begin{array}{l} \quad T(n) \\ =\Theta(n(1+\int_{1}^n \frac{x\lg{x}}{x^{2}} dx)) \\ =\Theta(n(1+\frac{1}{2}\lg^2{n})) \\ =\Theta(n\lg^2{n}) \end{array} T(n)=Θ(n(1+∫1nx2xlgxdx))=Θ(n(1+21lg2n))=Θ(nlg2n)
相关文章:

计算理论 复杂度预备知识
文章目录计算理论 复杂度预备知识符号递归表达式求解通项公式主方法Akra-Bazzi 定理计算理论 复杂度预备知识 符号 f(n)o(g(n))f(n)o(g(n))f(n)o(g(n)) :∃c\exists c∃c ,当 nnn 足够大时, f(n)<cg(n)f(n)\lt cg(n)f(n)<cg(n) &#…...
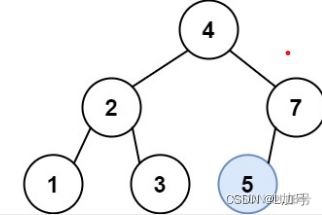
二叉树——二叉搜索树中的插入操作
二叉搜索树中的插入操作 链接 给定二叉搜索树(BST)的根节点 root 和要插入树中的值 value ,将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ,新值和原始二叉搜索树中的任意节点值都不同。 注意,…...

C# if break,if continue,if return的区别和使用
故事部分: 现在你肚子饿了,想要去: 1.吃个三菜一汤。 2.吃个蛋糕。 3.喝个奶茶。 结果,你吃饭的时候,吃到一个虫子。 你会有几种做法? 1.把有虫子这道菜拿走,继续吃下一道菜 。 2.算了ÿ…...

力扣-第二高的薪水
大家好,我是空空star,本篇带大家了解一道中等的力扣sql练习题。 文章目录前言一、题目:176. 第二高的薪水二、解题1.正确示范①提交SQL运行结果2.正确示范②提交SQL运行结果3.正确示范③提交SQL运行结果4.正确示范④提交SQL运行结果5.其他总结…...
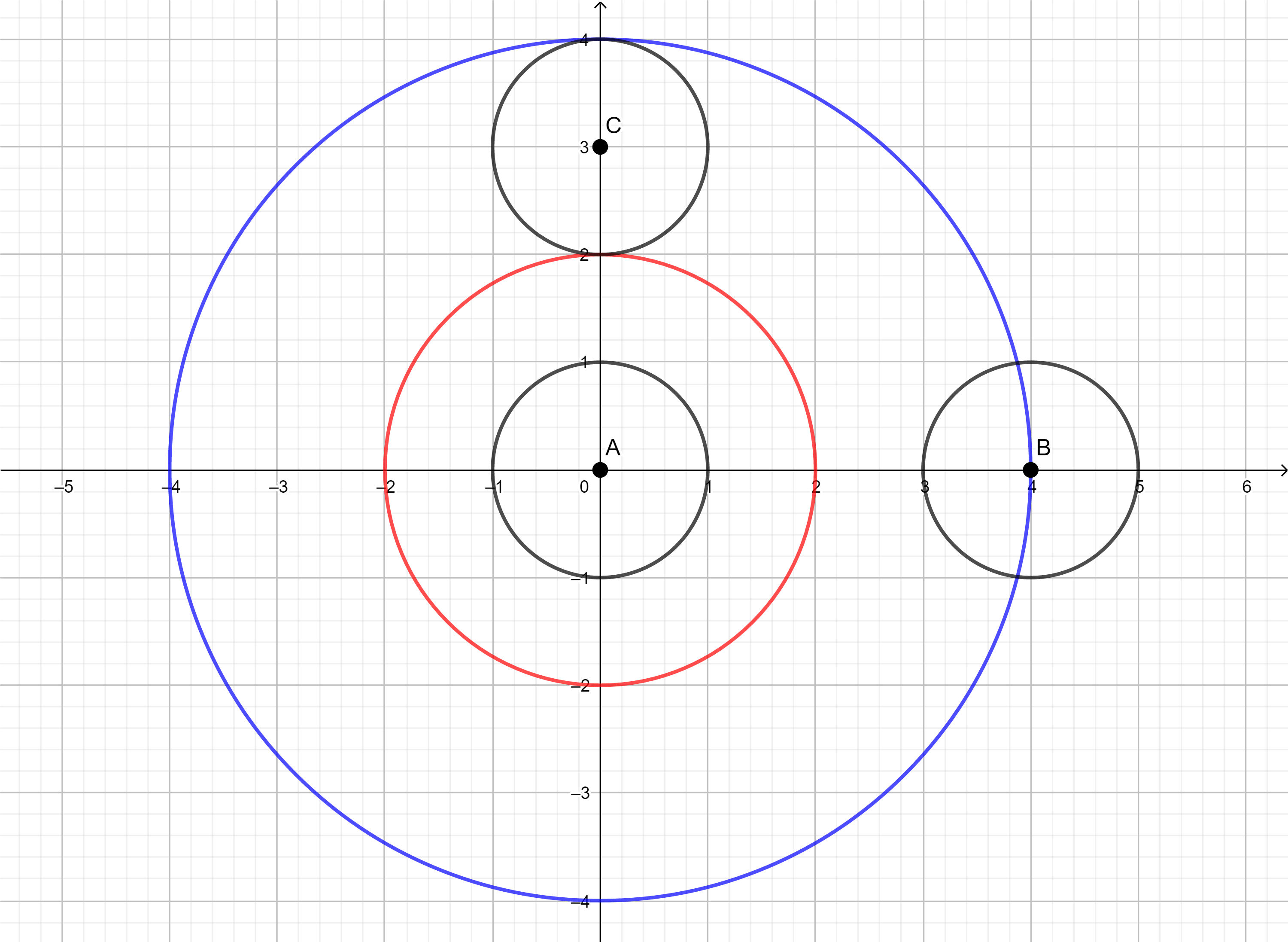
I - 太阳轰炸(组合数学Cnk n固定)
2023河南省赛组队训练赛(二) - Virtual Judge (vjudge.net) 背景:阿塔尼斯,达拉姆的大主教,在艾尔又一次沦陷之后指挥着星灵的最后一艘方舟舰:亚顿之矛。作为艾尔星灵数千年来的智慧结晶,亚顿之…...
centos安装gitlab
更新系统 sudo yum -y update安装所需要的包 sudo yum -y install epel-release curl vim policycoreutils-python如果要安装并使用本地Postfix服务器发送通知,请安装Postfix,这里就不安装了: sudo yum -y install postfix安装后启动并启用…...
)
【洛谷 P1093】[NOIP2007 普及组] 奖学金 题解(结构体排序)
[NOIP2007 普及组] 奖学金 题目描述 某小学最近得到了一笔赞助,打算拿出其中一部分为学习成绩优秀的前 555 名学生发奖学金。期末,每个学生都有 333 门课的成绩:语文、数学、英语。先按总分从高到低排序,如果两个同学总分相同,再…...
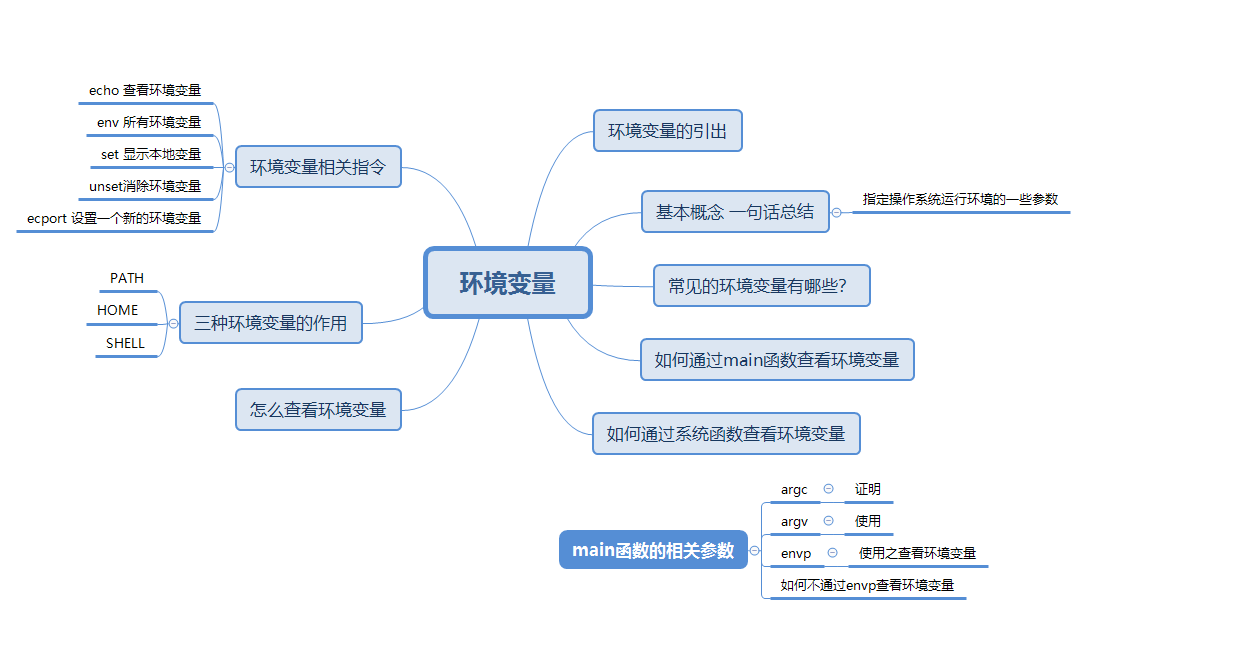
【Hello Linux】进程优先级和环境变量
作者:小萌新 专栏:Linux 作者简介:大二学生 希望能和大家一起进步! 本篇博客简介:简单介绍下进程的优先级 环境变量 进程优先级环境变量进程的优先级基本概念如何查看优先级PRI与NINI值的设置范围NI值如何修改修改方式…...

日期:Date,SimpleDateFormat常见API以及包装类
一.Date类 package com.gch.d1_date;import java.util.Date;/**目标:学会使用Date类处理时间,获取时间的信息*/ public class DateDemo1 {public static void main(String[] args) {// 1.创建一个Date类的对象:代表系统此刻日期时间对象Date d new Date();System.out.println(…...
嵌入式之ubuntu终端操作与shell常用命令详解
目录 文件和目录列表 基本列表功能 显示列表长度 过滤输出列表 浏览文件系统 Linux 文件系统 遍历目录 处理文件 创建文件 复制文件 制表键自动补全 重命名文件 删除文件 处理目录 创建目录 删除目录 编辑其他常用命令与操作 Uname命令 clear命令 返回上一级命令 显…...

【Shell学习笔记】6.Shell 流程控制
前言 本章介绍Shell的流程控制。 Shell 流程控制 和 Java、PHP 等语言不一样,sh 的流程控制不可为空,如(以下为 PHP 流程控制写法): 实例 <?php if (isset($_GET["q"])) {search(q); } else {// 不做任何事情 }在 sh/bash…...
27k入职阿里测开岗那天,我哭了,这5个月付出的一切总算没有白费~
先说一下自己的个人情况,计算机专业,16年普通二本学校毕业,经历过一些失败的工作经历后,经推荐就进入了华为的测试岗,进去才知道是接了个外包项目,不太稳定的样子,可是刚毕业谁知道什么外包不外…...

服务端开发之Java备战秋招面试篇5
努力了那么多年,回头一望,几乎全是漫长的挫折和煎熬。对于大多数人的一生来说,顺风顺水只是偶尔,挫折、不堪、焦虑和迷茫才是主旋律。我们登上并非我们所选择的舞台,演出并非我们所选择的剧本。继续加油吧! 目录 1.ArrayList与LinkedList区别, 应用场景…...

有趣的 Kotlin 0x11: joinToString,你真的了解嘛?
前言 之前使用 joinToString 函数也就是用逗号连接集合元素形成字符串,也没有细看它的参数,但是今天和 ChatGPT 聊天时,发现它给我输出了诸多内容。 joinToString joinToString()是Kotlin中一个非常有用的函数,它可以将集合的元…...
代码随想录算法训练营day46 | 动态规划之背包问题 139.单词拆分
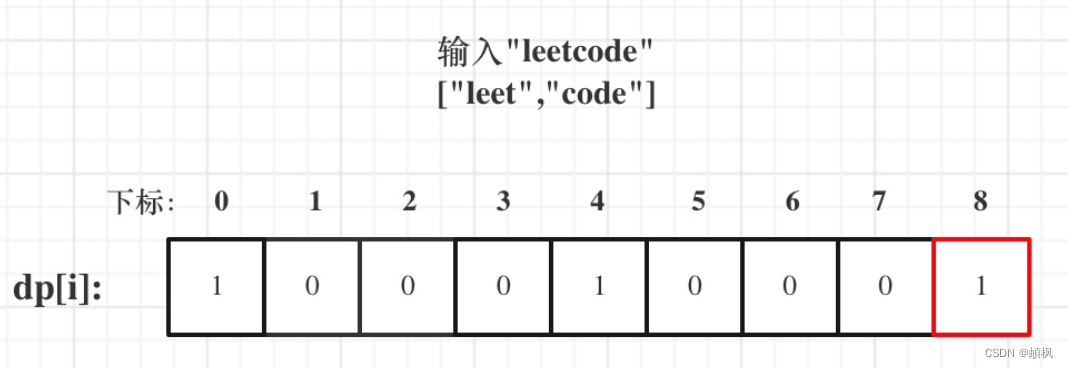
day46139.单词拆分1.确定dp数组以及下标的含义2.确定递推公式3.dp数组如何初始化4.确定遍历顺序5.举例推导dp[i]139.单词拆分 题目链接 解题思路:单词就是物品,字符串s就是背包,单词能否组成字符串s,就是问物品能不能把背包装满。…...

DPDK中的无锁共享数据结构
目录背景解决方法共享内存无锁操作新/老共享数据结构rte_ringrefcnt延迟释放方法1:读的线程来释放方法2:释放线程等到读线程轮询一轮参考背景 dpvs多线程,如何做到节约内存、高性能之间的均衡。 解决方法 共享内存 多线程共享内存&#x…...
【使用两个栈实现队列】
文章目录一、栈和队列的基本特点二、基本接口函数的实现1.栈的接口2.创建队列骨架3.入队操作4.取出队列元素5.返回队首元素6.判断队列是否为空7.销毁队列总结一、栈和队列的基本特点 栈的特点是后进先出,而队列的特点是先进先出。 使用两个栈实现队列,必…...
web,h5海康视频接入监控视频流记录一
项目需求,web端实现海康监控视频对接接入,需实现实时预览,云台功能,回放功能。 web端要播放视频,有三种方式,一种是装浏览器装插件,一种是装客户端exe,还有就是无插件了。浏览器装插…...

做毕业设计,前端部分你需要掌握的6个核心技能
其实前端新手如果想要自己实现一套毕业设计项目并非简单的事,因为之前很多人一直还停留在知识点的阶段,而且管理系统和C端网站都需要开发,但现在需要点连成线了。所以在启动项目开发之前呢,针对前端部分,我列举一些非常…...
--EventLoop and thread model)
Read book Netty in action(Chapter VIII)--EventLoop and thread model
前言 简单地说,线程模型指定了操作系统、编程语言、框架或者应用程序的上下文中的线程管理的关键方面。显而易见地,如何以及何时创建线程将对应用程序代码的执行产生显著的影响,因此开发人员需要理解与不同模型相关的权衡。无论是他们自己选…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

stm32wle5 lpuart DMA数据不接收
配置波特率9600时,需要使用外部低速晶振...
