当前位置： 首页 > news >正文

npm管理发布包-创建与发布

news 2026/2/9 22:06:13

创建与发布

我们可以将自己开发的工具包发布到 npm 服务上，方便自己和其他开发者使用，操作步骤如下

  1. 创建文件夹，并创建文件indexjs，在文件中声明函数，使用 module.exports 暴露
  2. npm初始化工具包，package.json 填写包的信息(包的名字是唯一的)
  3. 注册账号 https://www.npmjs.com/signup
  4. 激活账号 (一定要激活账号 )
  5. 修改为官方的官方镜像(命令行中运行 nrm use npm )
  6. 命令行下 npm login 填写相关用户信息
  7. 命令行下npm publish 提交包

更新包

后续可以对自己发布的包进行更新，操作步骤如下

  1. 更新包中的代码
  2. 测试代码是否可用
  3. 修改 package.json 中的版本号
  4. 发布更新
npm publish

删除包

npm unpublish --force

删除包需要满足一些条件：

  1. 不超过24小时
  2. 单周下载量小于300，同时维护者只有一个人
  3. 不依赖其他包

扩展内容

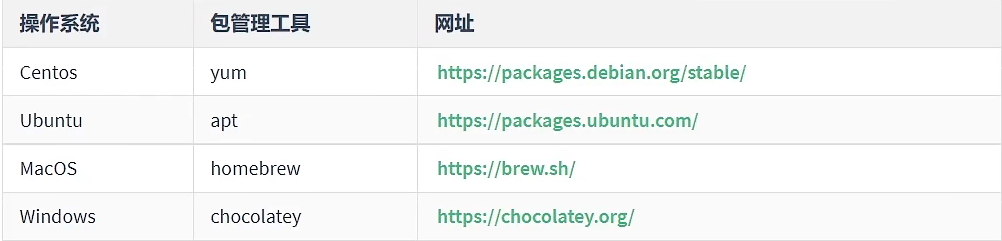
很多语言都有包管理工具比如：

语言包管理工具
PHPcomposer
Pythonpip
Javamaven
Javascriptnpm/yarn/cnpm/other
RubyrubyGems

除了编程语言领域有包管理工，操作系统层面也存在包管理不过这个包指的是[软件包
在这里插入图片描述

相关文章：

npm管理发布包-创建与发布

创建与发布 我们可以将自己开发的工具包发布到 npm 服务上，方便自己和其他开发者使用，操作步骤如下 创建文件夹，并创建文件indexjs，在文件中声明函数，使用 module.exports 暴露npm初始化工具包，package.j…...

编程日记 2023/12/2 1:50:24

基于Spring，SpringMVC，MyBatis的校园二手交易网站

文章目录 项目介绍主要功能截图：部分代码展示设计总结项目获取方式🍅 作者主页：超级无敌暴龙战士塔塔开 🍅 简介：Java领域优质创作者🏆、 简历模板、学习资料、面试题库【关注我，都给你】 🍅文末获取源码联系🍅 项目介绍 基于Spring，SpringMVC，MyBatis的校园二…...

编程日记 2023/12/2 1:49:23

酒店 KPI绩效考核指标及应用

“路遥知马力，日久见人心”，目前国内各类型酒店风起云涌，大有在市场竞争中一比高下之势，各路精英受经济型酒店低投入高回报的市场利益驱动，都分分抢占市场，从而使国内经济型酒店的数量不断增加，…...

编程日记 2023/12/2 1:44:19

WordPress两种方法实现上传媒体图片文件自动重命名

我们发布文章时，会上传一些图片、音频之类的文件。但是WordPress没有自动 给新上传文件重命名的功能，逐个文件去重命名那就太麻烦了，那么我们改如何自动给上传的媒体文件图片重命名呢？ 我在网站搜索了些上WordPress上传媒体文件自…...

编程日记 2023/12/2 1:43:18

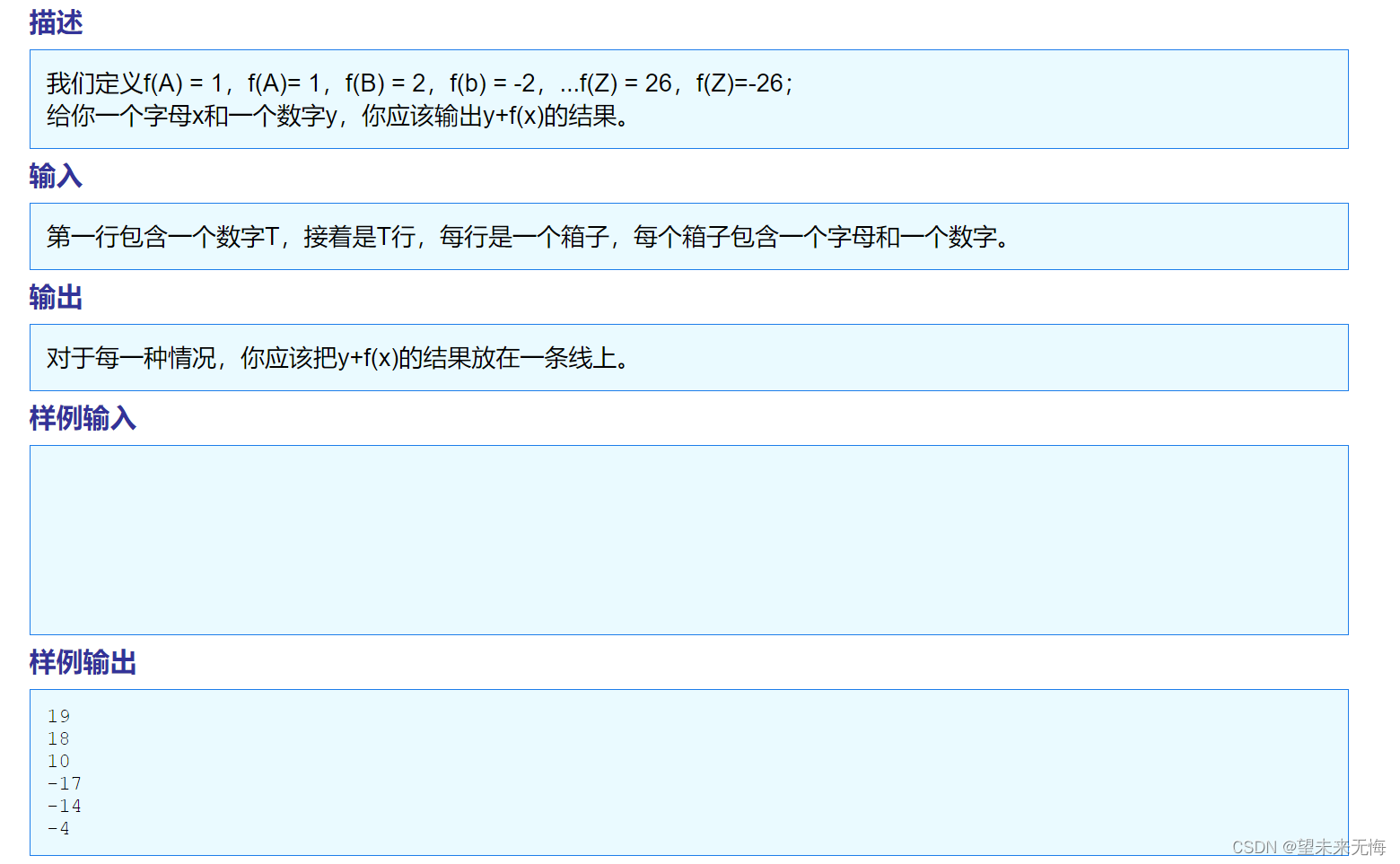
TZOJ 1405 An easy problem

翻译有些出错&#xff0c;但大概是那个意思 答案&#xff1a; #include <stdio.h> #include <ctype.h> //引用库函数isupper的头文件int main() {int T 0, i 0;scanf("%d", &T); //要输入的行数while (T--) //循环T次{char c;int y 0…...

编程日记 2023/12/2 1:42:18

SpringBoot+mysql+vue实现大学生健康档案管理系统前后端分离

一、项目简介 本项目是一套基于SpringBoot实现大学生健康档案管理系统&#xff0c;主要针对计算机相关专业的正在做bishe的学生和需要项目实战练习的Java学习者。 包含&#xff1a;项目源码、数据库脚本等&#xff0c;该项目可以直接作为bishe使用。 项目都经过严格调试&#…...

编程日记 2023/12/2 1:40:16

CCC联盟数字车钥匙（三）——UWB MAC时间网格同步及Hopping

本文继续上一篇UWB MAC时间网格继续介绍UWB MAC中关于时间同步相关内容。 3、MAC时间网格同步 每个测距会话的定义都基于相对的指定时钟参考 U W B t i m e 0 k UWB^k_{time0} UWBtime0k​&#xff0c;相对于发起者的内部时钟定义。 时钟参考 U W B t i m e 0 k UWB^k_{time0} …...

编程日记 2023/12/2 1:39:15

一周上手 steam搬砖项目或成2024年最受欢迎副业

蒸汽砖拆除项目&#xff0c;兼职创业两不误&#xff0c;助你轻松赚钱 你是否想要找到一个既可以兼职又可以创业的项目&#xff1f;蒸汽砖拆除项目正逐渐崭露头角&#xff0c;引起了越来越多人的关注。这个项目不仅门槛低&#xff0c;上手快&#xff0c;而且不用担心卖不出去&am…...

编程日记 2023/12/2 1:37:13

java数据结构（哈希表—HashMap）含LeetCode例题讲解

目录 1、HashMap的基本方法 1.1、基础方法&#xff08;增删改查&#xff09; 1.2、其他方法 2、HashMap的相关例题 2.1、题目介绍 2.2、解题 2.2.1、解题思路 2.2.2、解题图解 2.3、解题代码 1、HashMap的基本方法 HashMap 是一个散列表&#xff0c;它存储的内容是键…...

编程日记 2023/12/2 1:36:13

快速了解ChatGPT（大语言模型）

目录 GPT原理&#xff1a;文字接龙&#xff0c;输入一个字&#xff0c;后面会接最有可能出现的文字。 GPT4 学会提问&#xff1a;发挥语言模型的最大能力 参考李宏毅老师的课快速了解大语言模型做的笔记&#xff1a; Lee老师幽默的开场&#xff1a; GPT&#xff1a;chat Ge…...

编程日记 2023/12/2 1:34:10

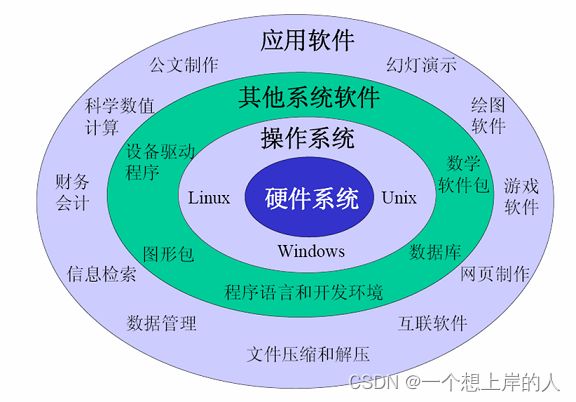
计算机软件的分类

以功能进行分类&#xff0c;计算机软件通常可以分为系统软件和应用软件两大类。 系统软件&#xff1a;系统软件是计算机运行和管理的基本软件&#xff0c;包括操作系统、驱动程序、系统工具和服务程序等。操作系统是系统软件的核心&#xff0c;负责管理计算机的硬件资源、提供用…...

编程日记 2023/12/2 1:33:09

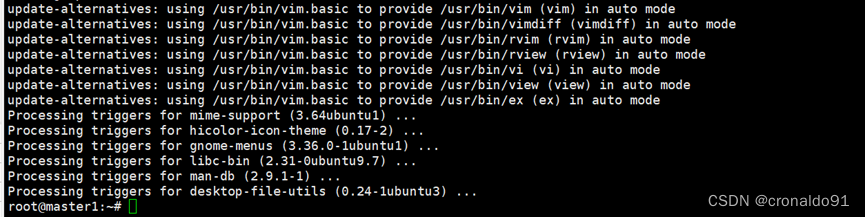
数据库应用：Ubuntu 20.04 安装MongoDB

目录 一、理论 1.MongoDB 二、实验 1.Ubuntu 20.04 安装MongoDB 三、问题 1.Ubuntu Linux的apt 包管理器更新安装软件报错 2.Ubuntu20.04安装vim报错 3.Ubuntu20.04如何更换阿里源 4.Ubuntu22.04如何更换阿里源 一、理论 1.MongoDB &#xff08;1&#xff09;概念 …...

编程日记 2023/12/2 1:32:08

服务器配置 jupyter lab，并在本地浏览器免密登陆

一、背景 快速搭建一个jupyter lab 不用每次用ssh登录输入密码 二、步骤 方法1、临时在服务器启动 jupyter lab&#xff0c;并在本地浏览器免密登陆 两句命令解决 pip install jupyterlabnohup jupyter lab --ServerApp.ip"*" --ServerApp.password"" -…...

编程日记 2023/12/2 1:30:06

WebUI自动化学习(Selenium+Python+Pytest框架)002

新建项目 New Project 新建一个python代码文件 file-new-python file 会自动创建一个.py后缀的代码文件 注意:命名规则,包含字母、数字、下划线&#xff0c;不能以数字开头&#xff0c;不能跟python关键字或包名重复。 ********************华丽分割线********************…...

编程日记 2023/12/2 1:28:04

miot-plugin-sdk. npm install安装失败

miot-plugin-sdk-npm install安装失败 最紧公司要开发一台智能设备&#xff0c;经过同事的对比&#xff0c;选中了米家作为云平台&#xff0c;于是&#xff0c;我就负责开发app界面端&#xff0c;根据官方文档教程 下载了miot-plugin-sdk 程序&#xff0c;准备开始开发,结果悲…...

编程日记 2023/12/2 1:27:03

抓取微信好友列表信息

本文实现的是一种较为安全、简洁、高效的抓取微信好友信息的方法。 实现工具&#xff1a;微信pc端、影刀RPA 主要流程&#xff1a; 手动—前期准备&#xff0c;电脑登陆微信&#xff0c;打开联系人页&#xff0c;使得联系人分类“A”显现在微信窗口界面 自动—运行程序&#…...

编程日记 2023/12/2 1:23:00

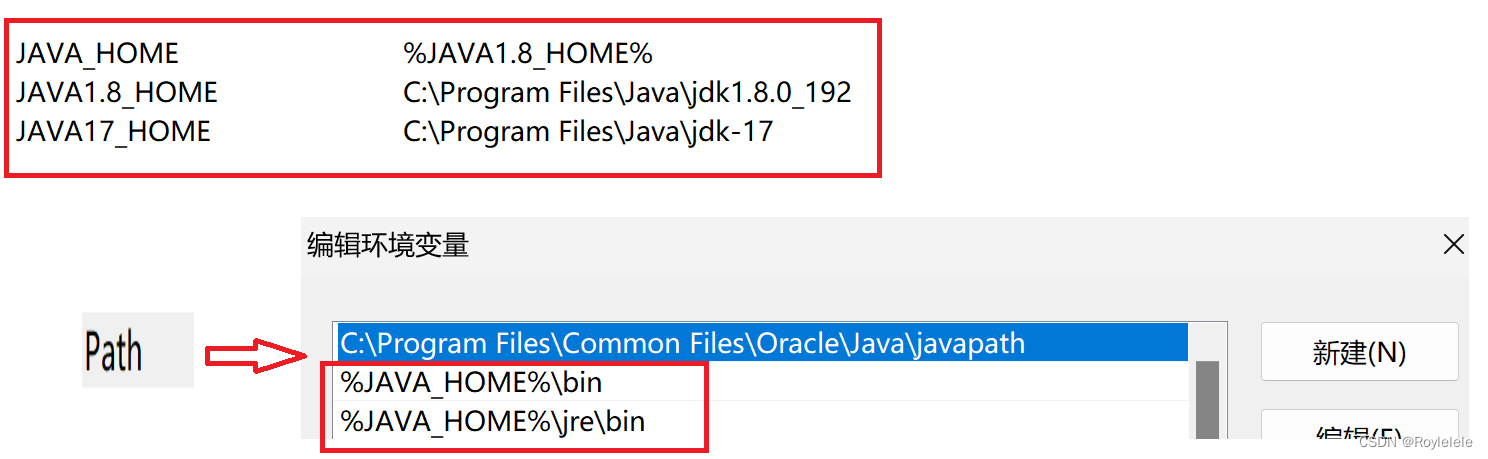
创建JDK8版本的SpringBoot项目的方法

目录 一.通过阿里云下载 二.通过IDEA创建 1.下载安装JDK17 2.创建SpringBoot 3.X的项目 3.把JDK17改成JDK8 截止到2023.11.24&#xff0c;SpringBoot不再支持3.0X之前的版本&#xff0c;3.0X之后的版本所对应的JDK版本为JDK17&#xff0c;下面介绍如何在idea上继续使用JDK…...

编程日记 2023/12/2 1:20:58

Python【走出棋盘】

要求&#xff1a; 某个人进入如下一个棋盘中&#xff0c;要求从左上角开始走&#xff0c; 最后从右下角出来&#xff08;要求只能前进&#xff0c;不能后退&#xff09;&#xff0c; 问题&#xff1a;共有多少种走法&#xff1f; 0 0 0 0 0 0 0 0 0 0 0 0 0 …...

编程日记 2023/12/2 1:11:50

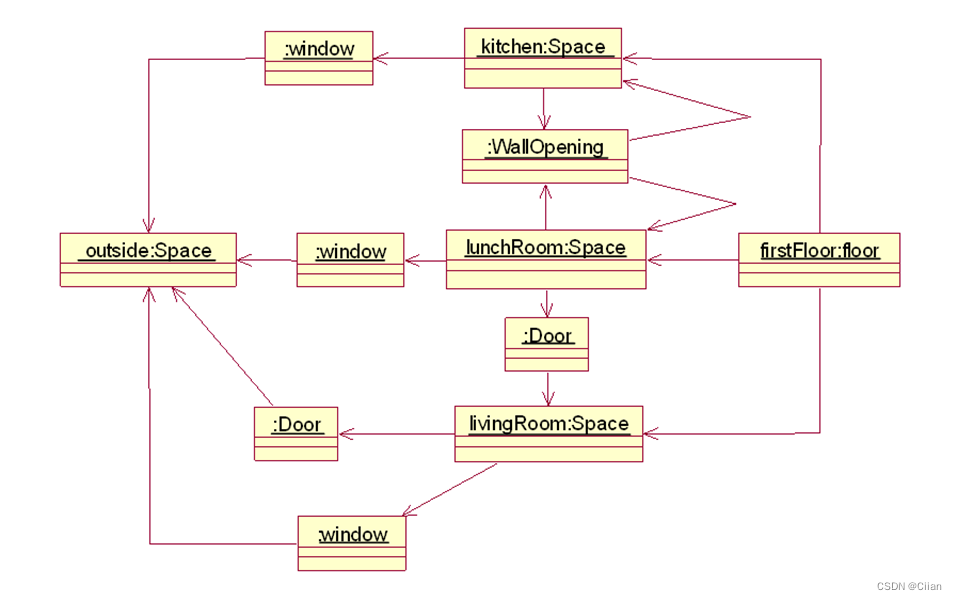
软件工程 - 第8章 面向对象建模 - 2 静态建模

静态建模&#xff08;类和对象建模&#xff09; 类和对象模型的基本模型元素有类、对象以及它们之间的关系。系统中的类和对象模型描述了系统的静态结构&#xff0c;在UML中用类图和对象图来表示。 类图由系统中使用的类以及它们之间的关系组成。类之间的关系有关联、依赖、泛…...

编程日记 2023/12/2 1:10:49

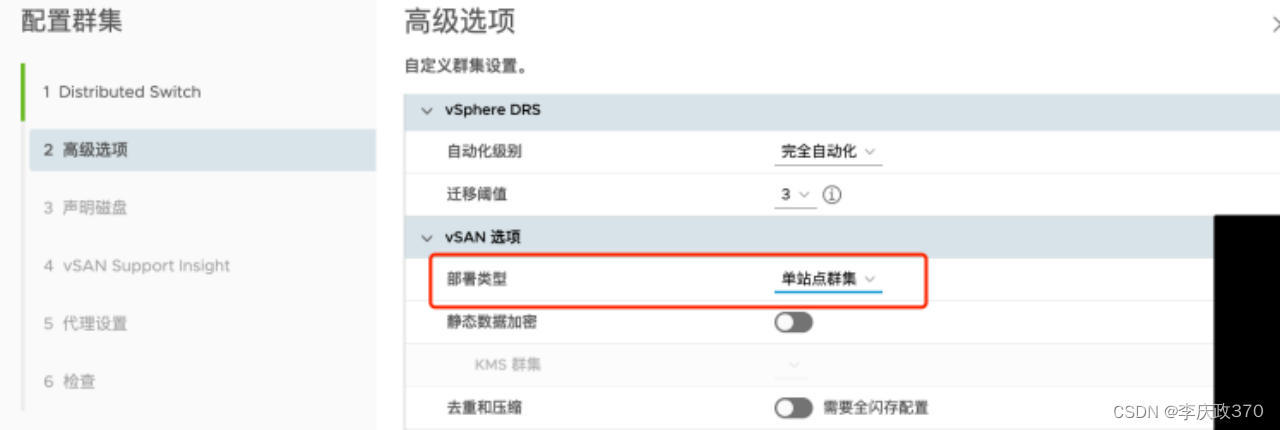
ESXi vSAN 整合多主机磁盘

VSAN 与 RAID区别&#xff1a; vSAN 可以管理 ESXi 主机&#xff0c;且只能与 ESXi 主机配合使用。一个 vSAN 实例仅支持一个群集。vSAN 不需要外部网络存储来远程存储虚拟机文件&#xff0c;例如光纤通道 (FC) 或存储区域网络 (SAN) 使用传统存储&#xff0c;存储管理员可以…...

编程日记 2023/12/2 1:08:47

Python：操作 Excel 折叠

💖亲爱的技术爱好者们，热烈欢迎来到 Kant2048 的博客！我是 Thomas Kant，很开心能在CSDN上与你们相遇～💖 本博客的精华专栏： 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

编程新知 2026/1/30 20:05:06

大型活动交通拥堵治理的视觉算法应用

大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动&#xff08;如演唱会、马拉松赛事、高考中考等&#xff09;期间&#xff0c;城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例&#xff0c;暖城商圈曾因观众集中离场导致周边…...

编程新知 2026/1/23 7:15:40

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍，多层嵌套定位示例

文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解（初学者版） 1. static（默认值） 2. relative（相对定位） 3. absolute（绝对定位） 4. fixed（固定定位） 5. sticky（粘性定位） 三、定位元素的层级关系（z-i…...

编程新知 2026/2/9 1:38:05

c#开发AI模型对话

AI模型 前面已经介绍了一般AI模型本地部署&#xff0c;直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型&#xff0c;但是目前国内可能使用不多&#xff0c;至少实践例子很少看见。开发训练模型就不介绍了&am…...

编程新知 2026/2/1 8:59:45

优选算法第十二讲：队列 + 宽搜 优先级队列

优选算法第十二讲&#xff1a;队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

编程新知 2026/1/20 17:18:59

网站指纹识别

网站指纹识别 网站的最基本组成&#xff1a;服务器&#xff08;操作系统&#xff09;、中间件&#xff08;web容器&#xff09;、脚本语言、数据厍 为什么要了解这些&#xff1f;举个例子&#xff1a;发现了一个文件读取漏洞&#xff0c;我们需要读/etc/passwd&#xff0c;如…...

编程新知 2026/2/2 17:06:29

JS设计模式(4)：观察者模式

JS设计模式(4):观察者模式 一、引入 在开发中&#xff0c;我们经常会遇到这样的场景&#xff1a;一个对象的状态变化需要自动通知其他对象&#xff0c;比如&#xff1a; 电商平台中&#xff0c;商品库存变化时需要通知所有订阅该商品的用户&#xff1b;新闻网站中&#xff0…...

编程新知 2025/9/1 6:48:07

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA

浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求&#xff0c;本次涉及的主要是收费汇聚交换机的配置&#xff0c;浪潮网络设备在高速项目很少&#xff0c;通…...

编程新知 2026/2/6 13:10:51

Java数值运算常见陷阱与规避方法

整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时，会出现小数部分被截断的情况。典型错误模式如下： void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

编程新知 2026/2/4 13:10:38

Chrome 浏览器前端与客户端双向通信实战

Chrome 前端&#xff08;即页面 JS / Web UI&#xff09;与客户端&#xff08;C 后端&#xff09;的交互机制&#xff0c;是 Chromium 架构中非常核心的一环。下面我将按常见场景&#xff0c;从通道、流程、技术栈几个角度做一套完整的分析&#xff0c;特别适合你这种在分析和改…...

编程新知 2026/2/4 16:47:57