【算法刷题】Day10
文章目录
- 15. 三数之和
- 题干:
- 算法原理:
- 1、排序 + 暴力枚举 + 利用set 去重
- 2、排序 + 双指针
- 代码:
- 18. 18. 四数之和
- 题干:
- 算法原理:
- 1、排序 + 暴力枚举 + 利用set 去重
- 2、排序 + 双指针
- 代码:
15. 三数之和


原题链接
题干:
存在一个三元组,满足
i != j、i != k 且 j != k
nums[i] + nums[j] + nums[k] == 0
算法原理:
1、排序 + 暴力枚举 + 利用set 去重
这个方法就是先循环,用几个 for 循环暴力枚举,然后放到 HashSet 中去重
但是这个方法时间复杂度很高,达到了O(N3)
2、排序 + 双指针
(1)排序
这里进行排序是为了从前向后遍历的时候,可以更好的用双指针进行操作
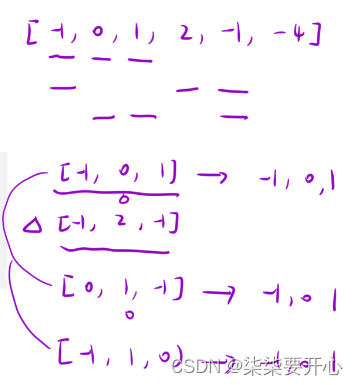
(2)固定一个数 a
这个 a 必须要大于等于 0,因为题目要求三数相加等于 0
(3)在该数后面的区间内,利用“双指针算法”快速找到两个数的和等于 -a 即可

(4)处理细节问题
-
不要漏任何一个组合
在 left 和 right 向中间走的时候,找到一个数等于固定的数的负数,不能停下,继续缩小区间,寻找下一个 -
去重
由于题目要求,不能返回相同的数组,所以要求去重
这样就可以找到一种结果之后,left 和 right 指针要跳过重复元素
当使用完一次双指正算法之后,也要跳过重复元素
但要注意避免越界!!!

代码:
public List<List<Integer>> threeSum(int[] nums) {List<List<Integer>> ret = new ArrayList<>();//1.排序Arrays.sort(nums);int n = nums.length;//2.利用双指针for (int i = 0; i < n;) {int left = i + 1;int right = n - 1;int target = -nums[i];if (nums[i] > 0) {break;}while (left < right) {int sum = nums[left] + nums[right];if (sum < target) {left++;}else if (sum > target) {right--;}else {ret.add(new ArrayList<Integer>(Arrays.asList(nums[i],nums[left],nums[right])));//缩小区间继续寻找left++;right--;while (left < right && nums[left] == nums[left-1]) {left++;}while (left < right && nums[right] == nums[right+1]) {right--;}}}i++;while (i < n && nums[i] == nums[i-1]) {i++;}}return ret;}
18. 18. 四数之和

题干:
这道题跟上面的三数之和非常相似,因此下面的解题思路也是非常相似
nums[a] + nums[b] + nums[c] + nums[d] == target
算法原理:
1、排序 + 暴力枚举 + 利用set 去重
这个算法依然是超时的,我们主要看第二种
2、排序 + 双指针
(1)排序
(2)在 a 后面的区间内,利用“三数之和”找到三个数(和上面题的方法一样),使这三个数的和等于 target - a
(3)处理细节问题
- 不漏
- 去重
代码:
public List<List<Integer>> fourSum(int[] nums, int target) {List<List<Integer>> ret = new ArrayList<>();int n = nums.length;//1.排序Arrays.sort(nums);//2.双指针for (int i = 0; i < n;) {long t1 = (long)target - nums[i];for (int j = i + 1; j < n;) {long t2 = t1 - nums[j];int left = j + 1;int right = n - 1;while (left < right) {int sum = nums[left] + nums[right];if (sum > t2) {right--;}else if (sum < t2) {left++;}else {ret.add(Arrays.asList(nums[i],nums[j],nums[left],nums[right]));left++;right--;while (left < right && nums[left] == nums[left-1]) {left++;}while (left < right && nums[right] == nums[right+1]) {right--;}}}j++;while (j < n && nums[j] == nums[j-1]) {j++;}}i++;while (i < n && nums[i] == nums[i-1]) {i++;}}return ret;}
相关文章:

【算法刷题】Day10
文章目录 15. 三数之和题干:算法原理:1、排序 暴力枚举 利用set 去重2、排序 双指针 代码: 18. 18. 四数之和题干:算法原理:1、排序 暴力枚举 利用set 去重2、排序 双指针 代码: 15. 三数之和 原题链…...
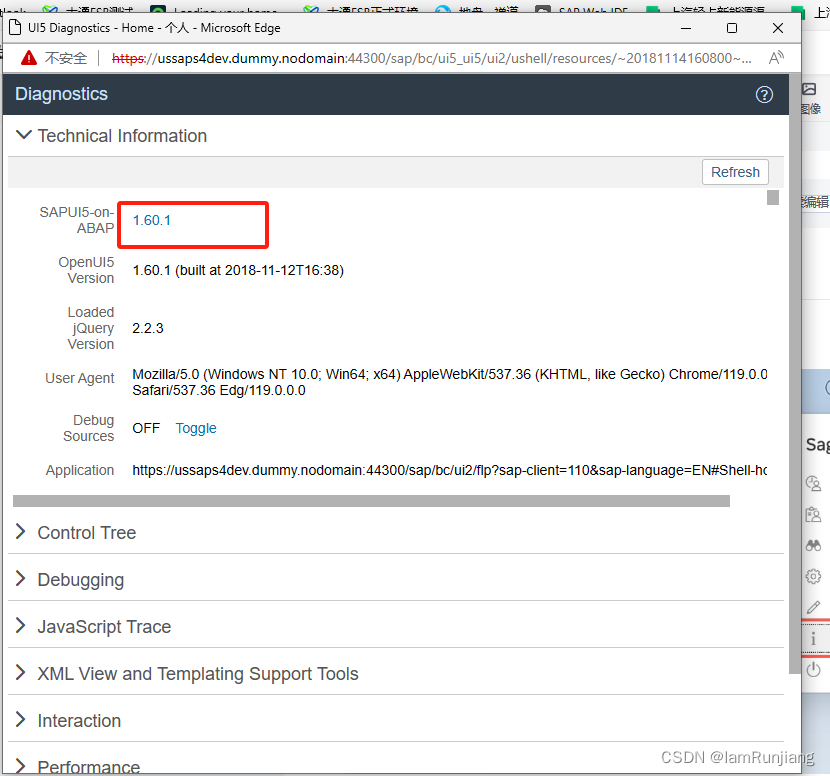
SAP 如何检查已安装的SAP UI5 版本
第一个方法是直接从FLP中查看 但是部分高版本的FLP中没有这个about, 那么在当前界面可以使用:CTRL ALT SHIFT S 查看当前版本 根据此版本,去进行你的UI5的开发吧...
15、 深度学习之正向传播和反向传播
上一节介绍了训练和推理的概念,这一节接着训练和推理的概念讲一下,神经网络的正向传播和反向传播。 其实单看正向传播和反向传播这两个概念,很好理解。 正向传播(Forward Propagation)是指从输入层到输出层的数据流动过程,而反向传播(Backpropagation)是指数据从输出…...

微信小程序中复制文本
在微信小程序中,可以使用wx.setClipboardData()方法来实现复制文本内容的功能。以下是一个示例代码: // 点击按钮触发复制事件 copyText: function() {var that this;wx.setClipboardData({data: 要复制的文本内容,success: function(res) {wx.showToa…...
vue3学习--初始
...
cmake和vscode 下的cmake的使用详解(二)
第四讲: GDB 调试器 前言: GDB(GNU Debugger) 是一个用来 调试 C/C 程序 的功能强大的 调试器 ,是 Linux 系统开发 C/C 最常用的调试器 程序员可以 使用 GDB 来跟踪程序中的错误 ,从而减少程序员的工作量。 Linux 开发 C/C …...

集成开发环境 PyCharm 的安装【侯小啾python领航班系列(二)】
集成开发环境PyCharm的安装【侯小啾python领航计划系列(二)】 大家好,我是博主侯小啾, 🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹…...
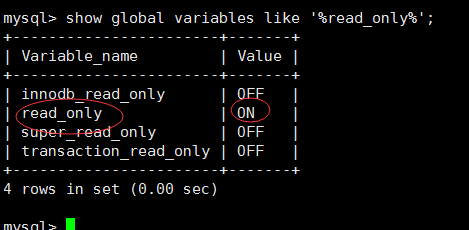
mysql从库设置为只读
直奔主题,mysql设置为只读后,无法增删改。 设置命令: mysql> set global read_only1; #1是只读,0是读写 mysql> show global variables like %read_only%; 以下是相关说明: 1、对于数据库读写状态…...
.NET6实现破解Modbus poll点表配置文件
📢欢迎点赞 :👍 收藏 ⭐留言 📝 如有错误敬请指正,赐人玫瑰,手留余香!📢本文作者:由webmote 原创📢作者格言:新的征程,我们面对的不仅仅是技术还有人心,人心不可测,海水不可量,唯有技术,才是深沉黑夜中的一座闪烁的灯塔 !序言 Modbus 协议是工控领域常见…...

【零基础入门Docker】Dockerfile中的USER指令以及dockerfile命令详解
✍面向读者:所有人 ✍所属专栏:Docker零基础入门专栏 目录 第 1 步:创建 Dockerfile 第 2 步:构建 Docker 镜像 第 3 步:运行 Docker 容器 第 4 步:验证输出 dockerfile命令详解 最佳实践 默认情况下…...

R语言期末考试复习二
上篇文章的后续!!!! http://t.csdnimg.cn/sqvYD 1.给向量vec1设置名为"A","B","C","D","E","F","G"。 2.将矩阵mat1的行名设置为"Row1"&#…...

golang Pool实战与底层实现
使用的go版本为 go1.21.2 首先我们写一个简单的Pool的使用代码 package mainimport "sync"var bytePool sync.Pool{New: func() interface{} {b : make([]byte, 1024)return &b}, }func main() {for j : 0; j < 10; j {obj : bytePool.Get().(*[]byte) // …...

WPF使用Prism框架批量注册Page,Window,UserControl等视图组件
前言 为了提高Prism框架下面的注册视图资源的简单性和提高后期可维护性,本文将使用prism自带的通过反射来批量注册视图资源,帮助我们快速高效的完成开发任务。 我们平常注册前端视图资源,一般都是在RegisterTypes方法里面,使用IContainerRegistry 的RegisterForNavigation…...

网络安全应急响应-Server2228(环境+解析)
网络安全应急响应 任务环境说明: 服务器场景:Server2228(开放链接)用户名:root,密码:p@ssw0rd123...

[WP] ISCTF2023 Web 部分题解
圣杯战争!!! 反序列化伪协议读取 where_is_the_flag 环境变量根目录当前目录 绕进你的心里 利用正则最大回溯绕过 easy_website or select 用双写绕过 空格用/**/绕,报错注入 wafr codesystem(ca\t /f*) webinclude 扫描得到index.bak备份文件打开为加密的代码 写…...
)
uniapp之Vue3配置跨域(代理)
在uni-app中,我们可以使用vue.config.js文件来配置跨域(代理)。以下是一个示例: // vue.config.js module.exports {devServer: {proxy: {/api: { // 这里填写你要代理的接口前缀,例如/apitarget: http://localhost:…...
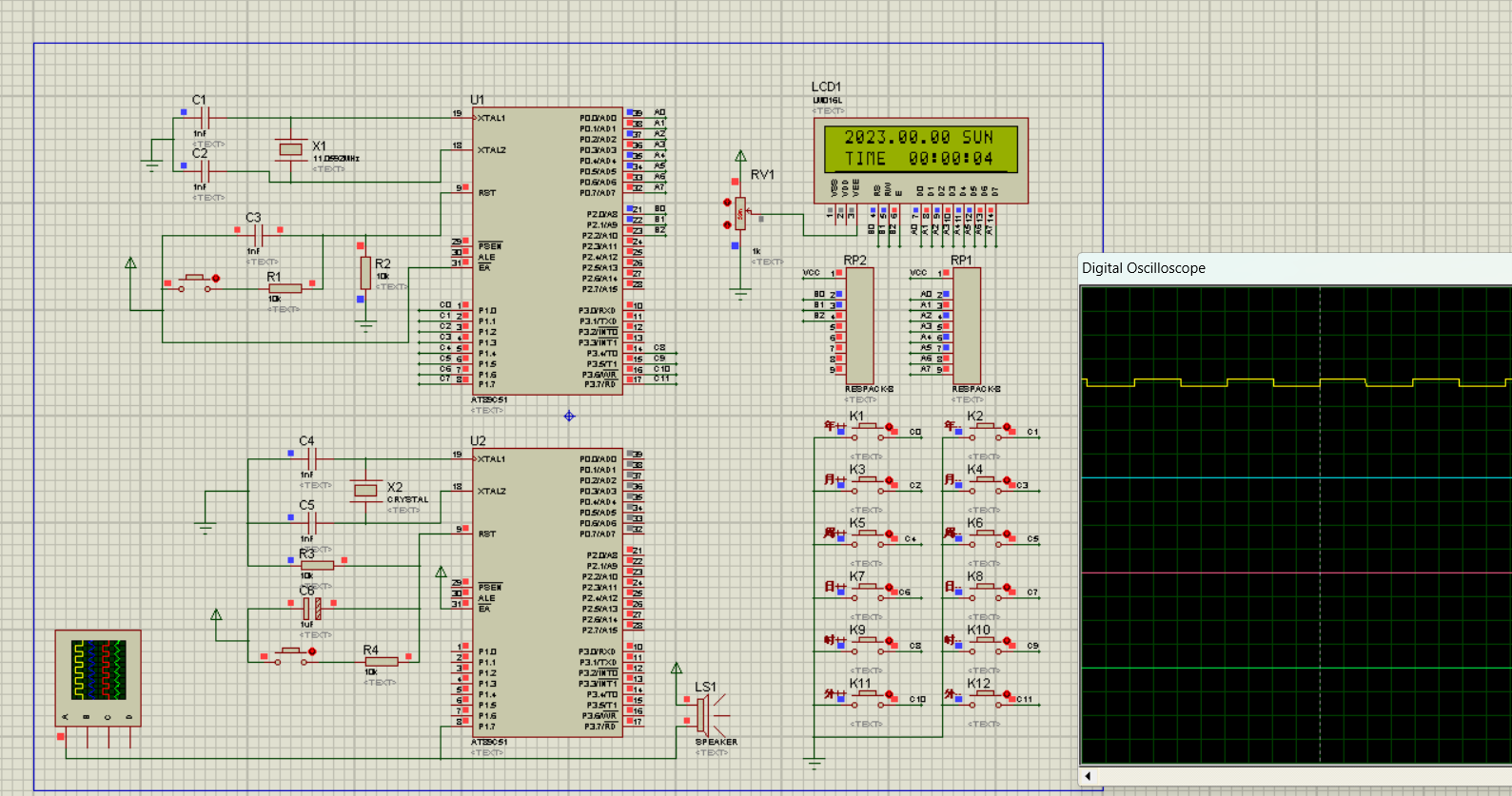
单片机实验(三)
前言 实验一:利用定时器T1的中断控制P1.7引脚输出音频信号,启动蜂鸣器发出一段熟悉的与众不同的具有10个音节的音乐音频。 实验二:使用定时器/计数器来实现一个LCD显示年、月、日、星期 、时、分、秒的电子表,要求时和分可以方便…...

Python 2进制按位取反
根据一checksum算法需要将一些参数按位取反 例:参数 13 数字13二进制为1101 [((x)) for x in str(bin(13))] [0, b, 1, 1, 0, 1] 除去0b字符串然后按位取反得到0010 [(1^int(x)) for x in str(bin(13)).replace(0b,)] [0, 0, 1, 0]然后将得到的2进制转换成十进制…...

【用Python根据用户名和手机号码生成Hash值并创建.cs .h和xlsx文件】
用Python根据用户名和手机号码生成Hash值并创建C Sharp .cs、嵌入式.h和xlsx表格文件 用Python根据用户名和手机号码生成Hash值并创建C Sharp .cs、嵌入式.h和xlsx表格文件,主要是为每个用户创建一个pubkey,并输出C Sharp C#和嵌入式 Keil的工程文件 pub…...
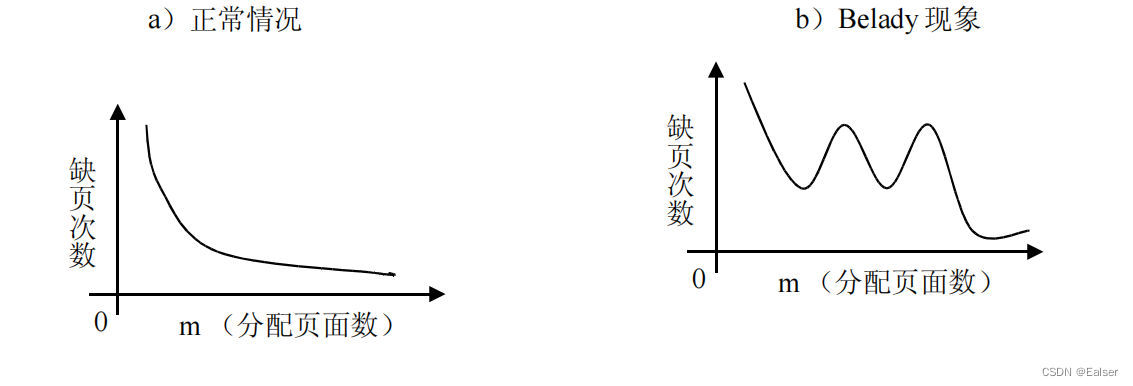
<Linux>(极简关键、省时省力)《Linux操作系统原理分析之存储管理(2)》(15)
[TOC](《Linux操作系统原理分析之存储管理(2)》(15) 5 存储管理5.4 分页存储管理5.4.1 纯分页存储管理a.页(页面)和物理块(帧)b. 页面大小c. 逻辑地址结构 5.5 存储扩充技术5.5.2 交…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...
