当前位置： 首页 > news >正文

笔记----单纯剖分----1

news 2025/11/7 16:29:15
  • 笔记----单纯剖分

定义

  • 线性组合
  • 仿射组合： 线性组合的系数为1
  • 凸组合： 仿射组合所有的系数都是正数
  • 凸集
    • R^m 的 任意有限个点的凸组合仍在其中的子集
  • 仿射子空间
    • R^m 的 任意有限个点的仿射组合仍在其中的子集
  • 凸包 conv(A)
    • A是R^m的一个子集 A的所有有限凸组合的集合为A的凸包
  • 仿射包 aff(A)
    • A是R^m的一个子集 A的所有有限仿射组合的集合为A的仿射包
  • 线性子空间 \begin{Bmatrix} x-c|x\in aff(C) \end{Bmatrix},c\in C
    • 其中定义dim\phi=-1
  • 仿射无关 
    • 如果有\sum_{i=0}^p\lambda_i=0.and.\sum_{i=0}^p\lambda x^i=0，则必有\lambda_0=...=\lambda_p=0，那么x^0,...,x^p仿射无关
  • p维闭单纯形
    • p+1个仿射无关的点的凸包
  • p维单纯形
    • 称p维闭单纯形在其仿射包中的相对内部为一个p维单纯形
  • 界面
  • 真面
  • 分割
  • 闭单纯形被相应的单纯形的所有面分割
  • 单纯剖分
    • C 是R^m 的一个凸集 dim C = n <= m。称G 是C 的一个单纯剖分 a simplicial triangulation 如果
      • G 是n维单纯形的一个集合
      • G 的所有单纯形的所有面组成C的一个分割
      • C 的每个点都有在C中的一个邻域只与G 中有限个单纯形相交

相关文章：

笔记----单纯剖分----1

笔记----单纯剖分 定义 线性组合仿射组合&#xff1a; 线性组合的系数为1凸组合&#xff1a; 仿射组合所有的系数都是正数 凸集 R^m 的 任意有限个点的凸组合仍在其中的子集仿射子空间 R^m 的 任意有限个点的仿射组合仍在其中的子集凸包 conv(A) A是R^m的一个子集 A的所有有限凸…...

编程日记 2023/12/2 15:12:53

mybatis源码（五）springboot pagehelper实现查询分页

1、背景 springboot的pagehelper插件能够实现对mybatis查询的分页管理&#xff0c;而且在使用时只需要提前声明即可&#xff0c;不需要修改已有的查询语句。使用如下&#xff1a; 之前对这个功能一直很感兴趣&#xff0c;但是一直没完整看过&#xff0c;今天准备详细梳理下。按…...

编程日记 2023/12/2 15:10:51

【BUG】SpringBoot项目Long类型数据返回前端精度丢失问题

问题描述 后端再给前端返回数据&#xff0c;使用Long类型的时候存在精度丢失问题。 原因分析&#xff1a; 分布式项目中广泛使用雪花算法生成ID作为数据库表的主键&#xff0c;Long类型的雪花ID有19位&#xff0c;而前端接收Long类型用的是number类型&#xff0c;但是number…...

编程日记 2023/12/2 15:05:47

UI自动化Selenium find_elements和find_element的区别

# 如果获取的element是list&#xff0c;那么需要用find_elements方法&#xff1b;此方法会返回list&#xff0c;然后使用len() 方法&#xff0c;计算对象的个数&#xff1b; # find_element方法返回的不是list对象&#xff0c;所以导致没办法计算对象个数 # 1.返回值类型不同…...

编程日记 2023/12/2 15:03:46

【Android】Window和WindowManager

文章目录 理解Window和WindowManagerWindow和WindowManagerWindow的内部机制Window的添加过程Window的删除过程Window的更新过程 Window的创建过程Activity的Window创建过程Dialog的Window创建过程Toast的Window创建过程 理解Window和WindowManager Window是一个抽象类&#xf…...

编程日记 2023/12/2 15:00:43

如何解决 Python ModuleNotFoundError 错误

模块对于开发 Python 程序很重要。 使用模块&#xff0c;我们可以分离代码库的不同部分以便于管理。 使用模块时&#xff0c;了解它们的工作方式以及如何将它们导入我们的代码非常重要。 如果没有这种理解或错误&#xff0c;我们可能会遇到不同的错误。 此类错误的一个示例是…...

编程日记 2023/12/2 14:58:41

Day62.算法训练

718. 最长重复子数组 class Solution {public int findLength(int[] nums1, int[] nums2) {int max 0;int[][] dp new int[nums1.length][nums2.length];for (int i 0; i < nums1.length; i) {for (int j 0; j < nums2.length; j) {if (nums1[i] nums2[j]) {if (i …...

编程日记 2023/12/2 14:56:39

Linux smbd命令教程：如何配置和管理Samba服务器（附案例详解和注意事项）

Linux smbd命令介绍 smbd是Samba套件的一部分。smbd是一个服务器守护进程&#xff0c;为Windows客户端提供文件共享和打印服务。服务器使用SMB&#xff08;或CIFS&#xff09;协议为客户端提供文件空间和打印服务。这与LanManager协议兼容&#xff0c;可以为LanManager客户端提…...

编程日记 2023/12/2 14:54:37

音视频学习(十九)——rtsp收流(tcp方式)

前言 本文主要介绍以tcp方式实现rtsp拉流。 流程图 流程说明: 客户端发起tcp请求&#xff0c;如向真实相机设备请求&#xff0c;端口一般默认554&#xff1b;tcp连接成功&#xff0c;客户端与服务端开始rtsp信令交互&#xff1b;客户端收到play命令响应后&#xff0c;开启线…...

编程日记 2023/12/2 14:53:37

LangChain（0.0.340）官方文档三：Prompts上——自定义提示模板、使用实时特征或少量示例创建提示模板

文章目录 一、 Prompt templates1.1 langchain_core.prompts1.2 PromptTemplate1.2.1 简介1.2.2 ICEL1.2.3 Validate template 1.3 ChatPromptTemplate1.3.1 使用role创建1.3.2 使用MessagePromptTemplate创建1.3.3 自定义MessagePromptTemplate1.3.3.1 自定义消息角色名1.3.3.…...

编程日记 2023/12/2 14:51:34

【算法】合并K个升序链表

这道题主要考察的是归并排序&#xff0c;因为已经升序过了&#xff0c;更好理解了。 当然也可以采用分治的思路&#xff1b;或采用最小堆的思路&#xff1b;面试中校招同学写出一种即可&#xff0c;如果能全概览讲一下&#xff0c;就更加分了。 #############################…...

编程日记 2023/12/2 14:49:32

持续集成交付CICD：GitLab Webhook触发Jenkins流水线

目录 一、实验 1.Jenkins远程下载GiaLab仓库代码 2.curl远程触发Jenkins流水线 3.GitLab Webhook触发Jenkins流水线 二、问题 1.GitLab配置Webhook时报错 一、实验 1.Jenkins远程下载GiaLab仓库代码 (1) Jenkins添加选项参数 (2)添加字符参数 (3)查看构建参数情况 (4)添…...

编程日记 2023/12/2 14:48:31

计算机网络测试题

一 单项选择题(5分) 1、假设要发送的数据为101110&#xff0c;采用CRC的生成多项式是X31&#xff0c;试求应添加在数据后面的余数。&#xff08;5分&#xff09; 110 011&#xff08;答案&#xff09; 101 001 实际得分&#xff1a;5分 二 填空题(95分) 1、以下3个子地址块…...

编程日记 2023/12/2 14:47:30

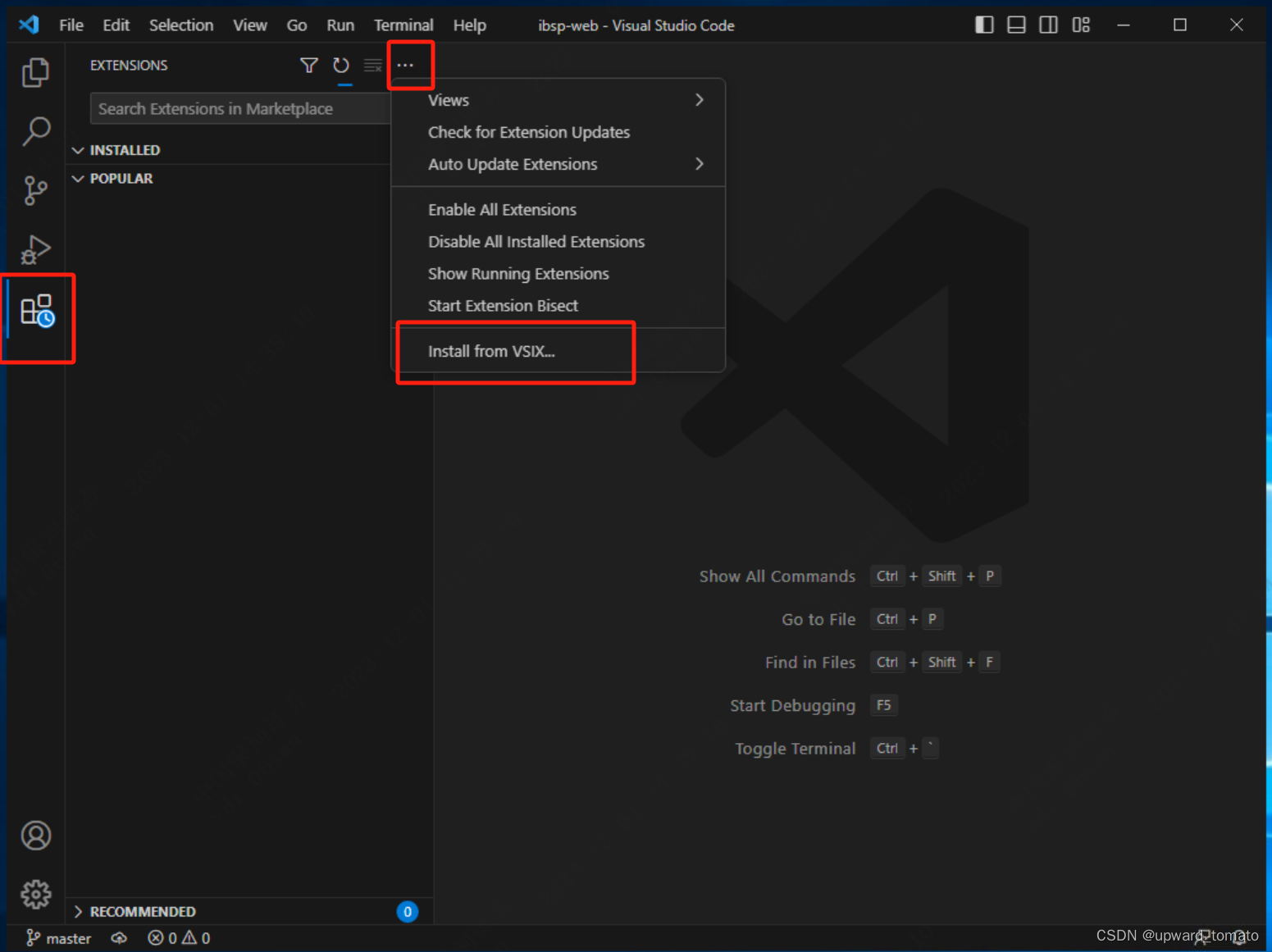
vscode如何在没有网络的情况下安装插件

vscode如何在没有网络的情况下安装插件 start 遇到没有网络的电脑&#xff0c;无法直接从插件市场安装vscode的插件。写一下 vscode 插件离线安装的方法. 解决方案 目标电脑没有可以安装插件的网络&#xff0c;那我们只能在有网络的环境下载好我们的插件。然后拷贝软件到无…...

编程日记 2023/12/2 14:46:29

自定义类型：结构体、联合、枚举

目录 一、⾃定义类型&#xff1a;结构体 1.结构体类型 1. 1结构体类型的声明 结构体变量的创建和初始化 1.2 结构的特殊声明 1.3 结构的自引用 2. 结构体内存对齐 ①&#xff1a;对齐规则 ②&#xff1a;offsetof函数 ③&#xff1a;为什么存在内存对⻬? ④ 修改默认对⻬…...

编程日记 2023/12/2 14:45:27

HelpLook可以作为wordpress的替代品，帮助企业快速搭建博客

博客作为一个非常有价值的平台&#xff0c;在当今的数字时代具有重要的意义。对于个人和企业来说&#xff0c;选择一款适合自己需求的专业博客搭建软件至关重要。本篇文章将会通过对比两个专业的博客搭建软件——HelpLook和WordPress&#xff0c;看看为什么我说HelpLook可以作为…...

编程日记 2023/12/2 14:43:25

单片机实现数码管动态显示

动态显示的特点是将所有位数码管的段选线并联在一起&#xff0c;由位选线控制是哪一位数码管有效。这样一来&#xff0c;就没有必要每一位数码管配一个锁存器&#xff0c;从而大大地简化了硬件电路。选亮数码管采用动态扫描显示。所谓动态扫描显示即轮流向各位数码管送出字形码…...

编程日记 2023/12/2 14:40:22

jbrowse基因组浏览器部署

一、jbrowse部署 1.1 jbrowse部署 sudo mkdir /var/www/jbrowse; sudo chown whoami /var/www/jbrowse; # cd into it cd /var/www/jbrowse;1.2 nginx配置 server {listen 80 default_server;listen [::]:80 default_server;server_name _;#root /var/w…...

编程日记 2023/12/2 14:39:21

神经网络 模型表示（一）

神经网络 模型表示 模型表示一 为了构建神经网络模型&#xff0c;我们需要首先思考大脑中的神经网络是怎样的&#xff1f;每一个神经元都可以被认为是一个处理单元/神经核&#xff08;processing unit/Nucleus&#xff09;&#xff0c;它含有许多输入/树突&#xff08;input/…...

编程日记 2023/12/2 14:38:21

【漏洞复现】智跃人力资源管理系统GenerateEntityFromTable.aspx接口存在SQL注入漏洞 附POC

漏洞描述 智跃人力资源管理系统是基于B/S网页端广域网平台，一套考勤系统即可对全国各地多个分公司进行统一管控，成本更低。信息共享更快。跨平台，跨电子设备。智跃人力资源管理系统GenerateEntityFromTable.aspx接口处存在SQL注入漏洞，攻击者可通过该漏洞获取数据库中的信…...

编程日记 2023/12/2 14:37:20

STM32+rt-thread判断是否联网

一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

编程新知 2025/9/23 20:06:08

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具

文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

编程新知 2025/10/21 3:16:48

ETLCloud可能遇到的问题有哪些？常见坑位解析

数据集成平台ETLCloud&#xff0c;主要用于支持数据的抽取&#xff08;Extract&#xff09;、转换&#xff08;Transform&#xff09;和加载&#xff08;Load&#xff09;过程。提供了一个简洁直观的界面&#xff0c;以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

编程新知 2025/11/7 15:18:11

SpringCloudGateway 自定义局部过滤器

场景&#xff1a; 将所有请求转化为同一路径请求&#xff08;方便穿网配置&#xff09;在请求头内标识原来路径&#xff0c;然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

编程新知 2025/10/30 22:13:49

Map相关知识

数据结构 二叉树 二叉树&#xff0c;顾名思义&#xff0c;每个节点最多有两个“叉”&#xff0c;也就是两个子节点&#xff0c;分别是左子 节点和右子节点。不过&#xff0c;二叉树并不要求每个节点都有两个子节点&#xff0c;有的节点只 有左子节点&#xff0c;有的节点只有…...

编程新知 2025/11/7 14:06:10

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波（Mean Shift Filtering）函数meanShiftFiltering()

操作系统&#xff1a;ubuntu22.04 OpenCV版本&#xff1a;OpenCV4.9 IDE:Visual Studio Code 编程语言&#xff1a;C11 算法描述 在 GPU 上对图像执行 均值漂移滤波&#xff08;Mean Shift Filtering&#xff09;&#xff0c;用于图像分割或平滑处理。 该函数将输入图像中的…...

编程新知 2025/11/2 8:58:17

AspectJ 在 Android 中的完整使用指南

一、环境配置&#xff08;Gradle 7.0 适配&#xff09; 1. 项目级 build.gradle // 注意&#xff1a;沪江插件已停更&#xff0c;推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

编程新知 2025/7/7 22:33:57

七、数据库的完整性

七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

编程新知 2025/11/7 14:17:30

代码规范和架构【立芯理论一】（2025.06.08）

1、代码规范的目标 代码简洁精炼、美观&#xff0c;可持续性好高效率高复用&#xff0c;可移植性好高内聚&#xff0c;低耦合没有冗余规范性&#xff0c;代码有规可循&#xff0c;可以看出自己当时的思考过程特殊排版&#xff0c;特殊语法&#xff0c;特殊指令&#xff0c;必须…...

编程新知 2025/11/3 2:33:44

【Android】Android 开发 ADB 常用指令

查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

编程新知 2025/8/17 23:35:19